Геймдев

#Руководства

14 май 2020
0

Уравниваем шансы: как работает случайность в играх

Люди очень плохи в оценке вероятностей. Разбираемся, как это влияет на игры и что с этим можно сделать.

vlada_maestro / shutterstock

Евгений Кучерявый

Пишет о программировании, в свободное время создаёт игры. Мечтает открыть свою студию и выпускать ламповые RPG.

В играх часто используются случайности: где-то от этого зависит вероятность попадания, а может, это игра с костями, в которой бросок определяет количество шагов за текущий ход.

Однако теория вероятности часто работает не так, как мы ожидаем. Самый простой пример — подбрасывание монетки. Если орёл выпал уже три раза подряд, то мы будем ожидать, что дальше будет решка. Однако предыдущие результаты никак не меняют вероятность следующих — она всё так же будет равна 50% для каждой из сторон.

Вы можете узнать больше о случайных числах, посмотрев этот ролик:

Какое абсолютно случайное число?

Создавая игру, мы сами решаем, как будет работать теория вероятностей. И мы можем изменить её так, чтобы помочь игрокам получить лучший опыт. Ну и чтобы в играх было меньше вот таких моментов:

Или даже таких:

Как в играх используется случайность

Самый простой пример — игра в кости. Вы кидаете кубики, на каждой грани которых изображено число (чаще всего число представлено в виде точек). Побеждает тот, кто получил число больше.

У игры в кости есть разные вариации, которые могут быть как самостоятельными играми, так и частью других игр. Например, покер с костями в «Ведьмаке»:

Вероятность выпадения каждой из граней — чуть больше 16%. Однако, поскольку кости можно подержать в руках, мы не так остро воспринимаем моменты, когда выпадает число, которое нас не устраивает.

На обычные числа, как правило, мы реагируем более резко. Рассмотрим это на примере игры, в которой необходимо уклоняться от ударов компьютера. Для этого нужно встать на одну из шести доступных клеток. Компьютер после каждого вашего хода случайным образом наносит удар по одной из этих клеток.

Вероятность, что компьютер промахнётся, равна 84%. Значит ли это, что из 100 попыток только 16 для игрока будут неудачными? Нет. Вполне возможно, что компьютер ни разу не попадёт или ни разу не промахнётся.

К сожалению, мы часто представляем числа не так, как они на самом деле работают. Поэтому если вероятность А больше вероятности Б, то мы ожидаем, что непременно выпадет А, а не Б.

И хотя в этой игре примерно тот же принцип, что в костях, мы будем думать, что система несправедлива, потому что она представлена в виде чисел, а не чего-то более осязаемого.

*Бурная реакция игрока на промах, несмотря на 99%-ную вероятность попадания*

Чтобы не гневать игроков так сильно, мы можем пойти на некоторые уловки.

Входная и выходная случайности

Случайность может быть двух видов: входная и выходная.

Входная случайность (input randomness) — это всё, что происходит до действий игрока. Например, как будет сгенерирован уровень в игре или как будет перемешана колода карт. Входную случайность можно также назвать предудачей (pre-luck).

Выходная случайность (output randomness) относится к успеху действий игрока. Например, вероятность попадания по врагу или выпавшее число. Выходную случайность можно также назвать постудачей (post-luck).

Два вида случайности в играх

Далее речь пойдёт в основном про выходную случайность, так как она обычно воспринимается игроками болезненнее, чем входная.

Как улучшить случайность в игре

Есть несколько способов изменить восприятие случайности игроками. Например, вы можете показывать заниженные числа: если на самом деле шанс успеха равен 99%, то игроку нужно показать 90% или меньше. Опять же, 90% мы воспринимаем как все 100%.

Если же нужно показать вероятность неудачи, то стоит завысить число — тогда игрок будет чувствовать, что у него получилось победить, хотя шансы были против него.

Второй вариант — использовать несколько «бросков». То есть вместо одного кубика бросать пять, как в покере из «Ведьмака», либо бросать один кубик несколько раз. Так игроку хотя бы раз повезёт получить крупное число и он не так сильно расстроится.

В случае с выстрелами можно отдельно просчитывать вероятность попадания каждой пули, а не целой очереди. Например, в Star Wars: Knights of the Old Republic 2 при использовании приёма Серия ударов урон и само попадание рассчитываются отдельно для каждого удара:

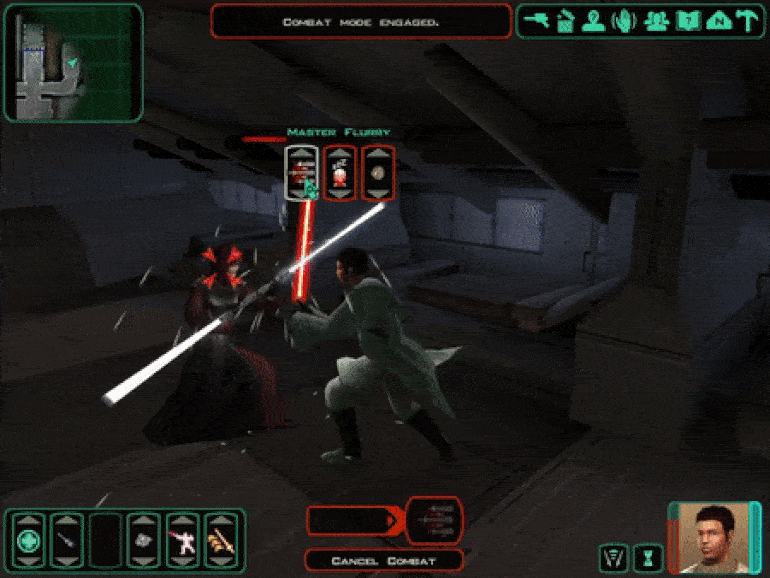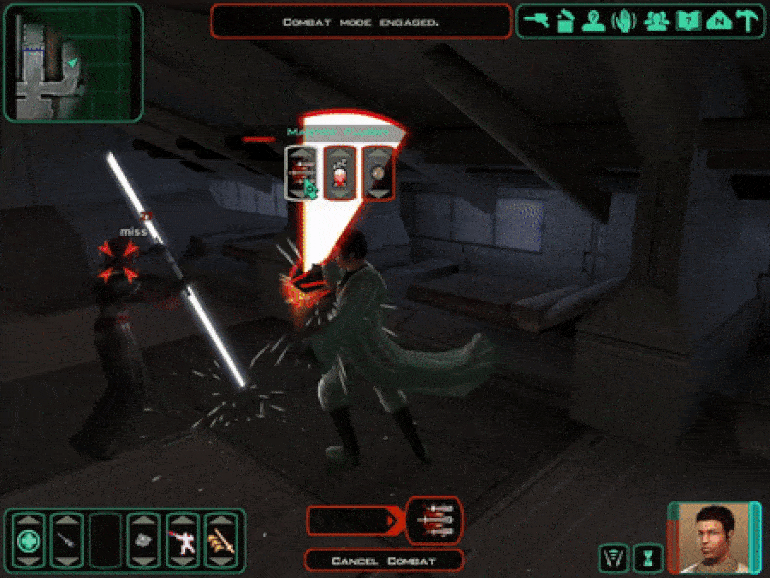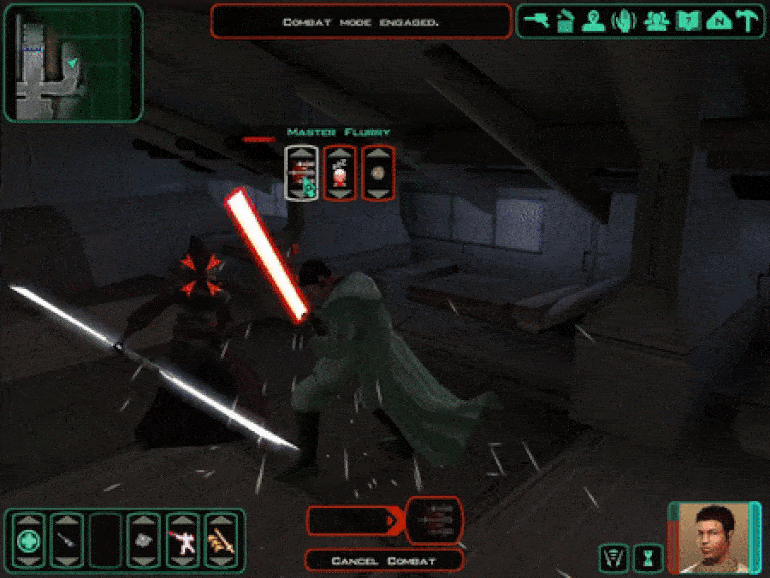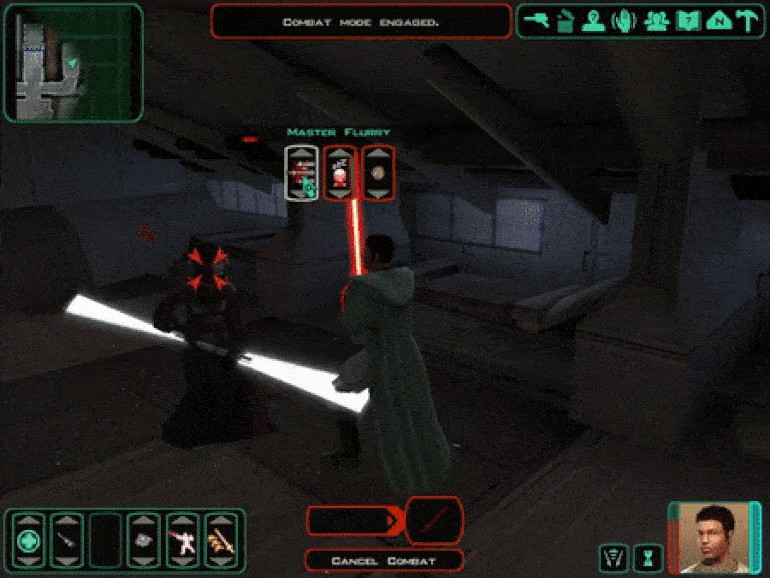
Третий вариант — обыграть всё это в сюжете. В TES V: Skyrim вы можете заниматься карманной кражей. Вероятность успеха зависит от разных параметров, а сам шанс успеха можно увидеть на экране.

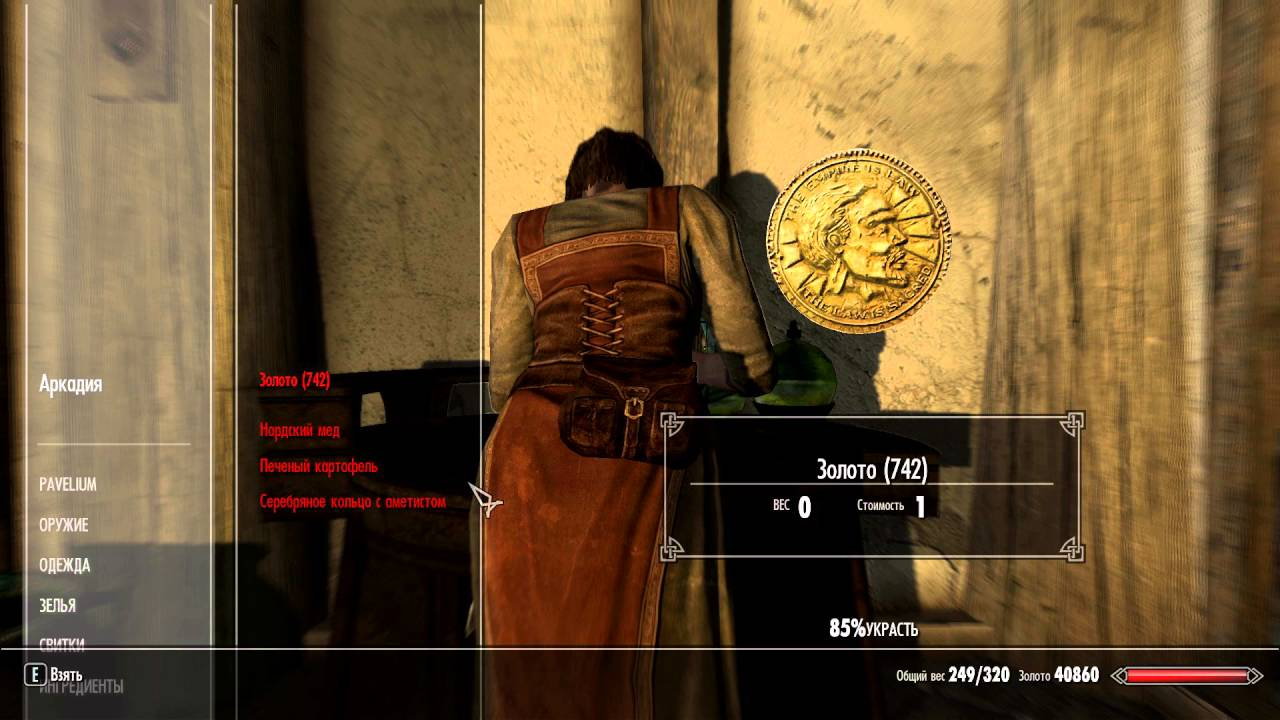
Кроме ваших навыков, магических эффектов и зачарованных предметов на вероятность успеха также влияет удача. В мире древних свитков удачей заведует даэдра (божество) Ноктюрнал.

Именно благодаря ей новичок может украсть что-то очень ценное, но она же может испортить планы профессионала. Если Ноктюрнал захочет, то и слепой старик сможет поймать вора за руку.

Также вы можете совсем переделать систему использования случайных чисел. В тетрисе, например, генерируются не отдельные блоки, а наборы по семь блоков. Это позволяет более «честно» выдавать фигуры. Похожий подход используется в Hateris, с тем лишь исключением, что игра анализирует ситуацию в игре и специально выдаёт худшие блоки.

Заключение

Несмотря на то что геймдизайн — это творческое занятие, в нём очень часто нужно применять математику. В основном это статистика и теория вероятности. Хорошее знание математики поможет вам создавать игры, которые будут казаться справедливыми — за счёт баланса и не совсем случайных случайностей.