Как работать с библиотекой SymPy в Python
Сессия близко! Знакомимся с мощным инструментом для решения диффуров, интегралов и матриц.


При решении математических и инженерных задач часто требуется провести аналитические вычисления: найти производную или интеграл, решить систему уравнений или упростить математическое выражение. Сделать это средствами стандартной библиотеки Python довольно тяжело — придётся написать много сложных математических функций.
Но зачем, если к проекту можно подключить SymPy? Вот о ней далее и поговорим.
Из этой статье вы узнаете:
Что такое SymPy
SymPy — это бесплатная библиотека для символьных вычислений на языке Python. В символьных вычислениях компьютер работает с уравнениями и выражениями как с последовательностью символов, тогда как в численных оперирует приближёнными числовыми значениями.
По сравнению с другими Python-библиотеками для математических вычислений, такими как SageMath и CasADi, у SymPy есть ряд преимуществ.
Работа с символьными вычислениями. Как уже было сказано выше, SymPy работает с математическими выражениями и формулами как с последовательностью символов, а не чисел. Это повышает точность математических операций и позволяет сформулировать результаты вычислений в аналитическом виде (с помощью формул, системы выражений и так далее).
Поддержка различных разделов математики: геометрии, тригонометрии, логики и других. В SymPy есть функции для алгебраического упрощения выражений, решения уравнений, дифференцирования, интегрирования, манипуляции с полиномами и матрицами и многое другое.
Лёгкая интеграция с другими библиотеками Python, такими как NumPy и Matplotlib. Вы можете комбинировать символьные вычисления с численными и визуализировать их без предварительной настройки.
Как установить SymPy
Перед тем как начать работу с библиотекой, установите Python на компьютер. Затем откройте терминал или командную строку и установите SymPy с помощью pip:
pip install sympyПодождите, пока процесс завершится. Откройте редактор кода или IDE и проверьте установку:
import sympy
print(sympy.__version__)
Если видите на экране номер версии SymPy, значит, библиотека установлена правильно.
Если работаете в среде Anaconda, то для установки библиотеки введите в командной строке следующее:
conda install —c anaconda sympy
Основные функции SymPy
Все функции библиотеки подробно описаны в документации. Мы же пройдёмся по самым часто используемым.
Создание символьных переменных и выражений
Символьные переменные создаются с помощью функции symbols():
from sympy import symbols
# Создаём символьные переменные x, y, z
x, y, z = symbols('x y z')
Аргумент функции — строка с символами, которые станут именами переменных в выражении. В нашем примере x, y, z — это символьные переменные. Обратите внимание: их имена задаются одной строкой через пробел.
Символьные выражения создаются путём комбинирования символьных переменных и арифметических операций:
from sympy import symbols
# Определение символьных переменных
x, y, z = symbols('x y z')
# Создание символьного выражения
expr = x**2 + 2 * y − z
Этот код создаёт символьные переменные x, y, z и содержащее их символьное выражение expr. Теперь expr можно упрощать, дифференцировать, интегрировать и далее по списку.
Внимание! Здесь и далее символы ** означают операцию возведения в степень.
Арифметические операции. Библиотека SymPy поддерживает основные арифметические операции с символьными выражениями:
from sympy import symbols
x, y, z = symbols('x y z')
# Сложение
expr_sum = x + y + z
# Вычитание
expr_diff = x − y
# Умножение
expr_mul = x * y
# Деление
expr_div = x / y
# Возведение в степень
expr_power = x**2
# Комбинированные операции
expr_combined = (x + y)**2 / (z - 1)
Математические константы используются в символьных выражениях для упрощения записи. Разберём несколько из них.
Пи (π) — отношение длины окружности к её диаметру:
from sympy import pi, symbols
# Создание символьной переменной
x = symbols('x')
# Использование константы π
expr_pi = pi * x
Бесконечность (∞) обозначается двумя символами — oo:
from sympy import oo, symbols
# Создание символьной переменной
x = symbols('x')
# Использование бесконечности
expr_infinity = x / oo
Подстановка. С помощью subs() можно подставлять числа в символьные переменные, чтобы получить значение выражений в конкретных точках:
from sympy import symbols
# Создание символьных переменных
x, y, z = symbols('x y z')
# Создание символьного выражения
expr = x + y**2 - z
# Подстановка значений
result = expr.subs({x: 2, y: 3, z: 1})
print(result) # 10
В этом примере команда expr.subs({x: 2, y: 3, z: 1}) заменяет x на 2, y на 3 и z на 1 в выражении expr.
Функцию subs() также можно использовать для подстановки символьных выражений:
from sympy import symbols, sin, pi
x, y = symbols('x y')
expr = x + sin(y)
# Подстановка символьного выражения pi/2
result = expr.subs({x: 2, y: pi/2})
print(result) # 3
Здесь expr.subs({x: 2, y: pi/2}) заменит x на 2, y — на символьное выражение π/2.
Манипуляции с символьными выражениями
SymPy предоставляет множество функций для работы с математическими выражениями: упрощение, раскрытие скобок, факторизация, сокращение дробей и так далее. Рассмотрим некоторые из них подробнее.
Упрощение. Пригодится, когда нужно представить выражение в более удобоваримой форме. Для этого есть функции: simplify, expand, collect и factor.
simplify() анализирует выражение на предмет вызова функций, квадратных корней, радикалов и степеней и инициализирует подходящие процедуры упрощения:
from sympy import symbols, simplify, sin, cos
x = symbols('x')
expr = sin(x)**2 + cos(x)**2 # Тождество Пифагора, равное 1 при любом x
simplified_expr = simplify(expr)
print(simplified_expr) # 1В этом примере simplify() упрощает выражение sin(x)**2 + cos(x)**2 с помощью тождества Пифагора. Обратите внимание, что не мы задаём вариант упрощения — он определяется автоматически.
Функция expand() раскрывает скобки:
from sympy import symbols, expand, factor
x, y = symbols('x y')
expr = (x + y)**3
expanded_expr = expand(expr)
print(expr, '=', expanded_expr)
В этом примере мы раскрыли куб выражения (x + y).
Вот какой результат вернул компьютер:
(x + y)**3 = x**3 + 3*x**2*y + 3*x*y**2 + y**3
Функция collect() группирует переменные в выражениях:
from sympy import symbols, collect
x, y = symbols('x y')
expr = x*y + x**2 + y + x*y**2
collected_expr = collect(expr, x)
print(expr, '=', collected_expr)
Здесь collect() группирует слагаемые в выражении x*y + x**2 + y + x*y**2 по степеням переменной x.
Результат выполнения кода:
x**2 + x*y**2 + x*y + y = x**2 + x*(y**2 + y) + y
factor() представляет выражение в виде произведения множителей (факторизует его):
from sympy import symbols, factor
x, y = symbols('x y')
expr = x**3 + 3 * x**2 * y + 3 * x * y**2 + y**3
factored_expr = factor(expr)
print(expr, '=', factored_expr)Результат:
x**3 + 3*x**2*y + 3*x*y**2 + y**3 = (x + y)**3
Все эти методы можно и нужно комбинировать, чтобы получить необходимый результат.
Решаем уравнения и системы уравнений
В SymPy можно решать уравнения с символьными переменными и их системы — с помощью функций Eq() и solve().
Уравнения
Допустим, мы хотим решить уравнение x**2 + y**2 = 1. Чтобы составить его, нам понадобится функция Eq():
from sympy import symbols, Eq, solve
# Создание символьных переменных
x, y = symbols('x y')
# Создание уравнения
equation = Eq(x**2 + y**2, 1)
Решить полученное уравнение можно с помощью функции solve():
# Решение уравнения
solution = solve(equation, y)
print(solution)
Код вернёт два решения квадратного уравнения в виде списка:
[-sqrt(1 - x**2), sqrt(1 - x**2)]
Системы уравнений
Добавим в нашу программу ещё одну символьную переменную (z) и построим систему уравнений:
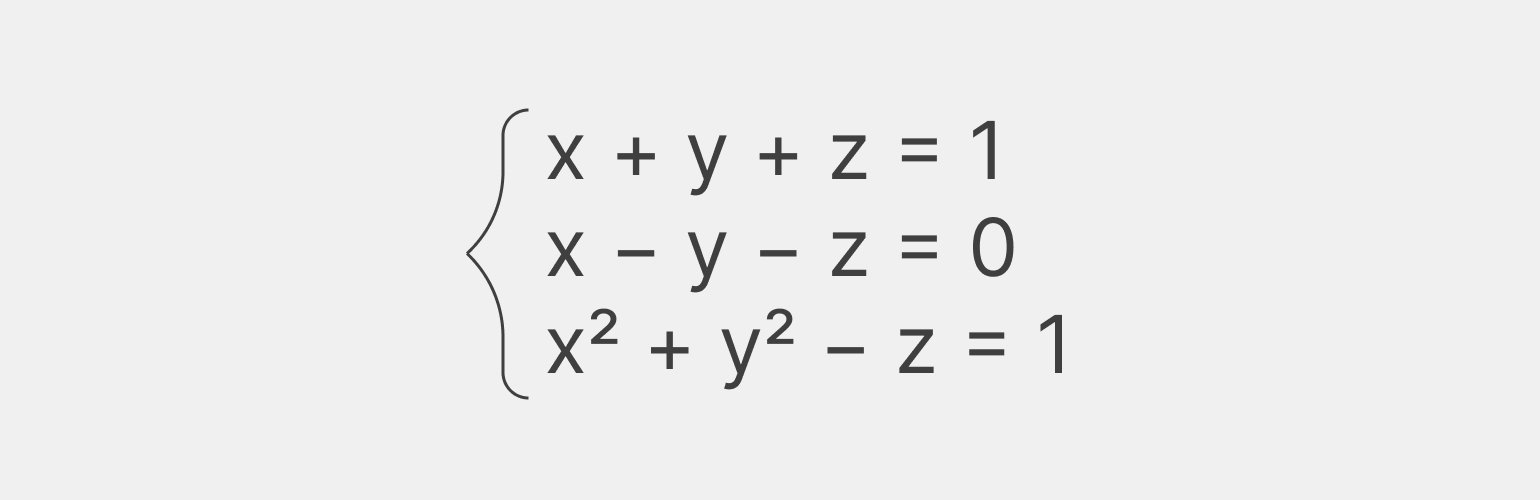
Делается это с помощью той же функции Eq():
from sympy import symbols, Eq, solve
# Создание символьных переменных
x, y = symbols('x y')
# Создание уравнения
equation = Eq(x**2 + y**2, 1)
# Создание ещё одной символьной переменной
z = symbols('z')
# Создание системы уравнений
system_of_equations = [Eq(x + y + z, 1), Eq(x - y - z, 0), Eq(x**2 + y**2 - z, 1)]
Теперь решим её с помощью уже знакомой функции solve():
# Решение системы уравнений
solutions = solve(system_of_equations, (x, y, z))
print(solutions)Программа вернёт значения переменных x, y, z, при которых выполняется система уравнений:
[(1/2, -1/2 + sqrt(6)/2, 1 - sqrt(6)/2), (1/2, -sqrt(6)/2 - 1/2, 1 + sqrt(6)/2)]Дифференциальные уравнения
С SymPy можно решать даже диффуры. Для этого в ней есть функция dsolve().
Давайте познакомимся с её работой на примере уравнения y’ = x**2 − y с начальным условием y(0) = 1:
from sympy import symbols, Function, dsolve, Eq
# Создание символов и функции
x = symbols('x')
y = Function('y')
# Определение дифференциального уравнения
diff_eq = Eq(y(x).diff(x), x**2 − y(x))
# Решение уравнения
solution = dsolve(diff_eq, y(x), ics={y(0): 1})
print(solution)
На экране увидим результат — символьное выражение:
Eq(y(x), x**2 − 2*x + 2 − exp(-x))
Операции с матрицами
Есть в SymPy и инструменты линейной алгебры. Например, для создания матриц, сложения, вычитания и прочих действий с ними используют класс Matrix.
Как создать матрицу
Для этого создайте объект Matrix, передав в него символы для заполнения матрицы:
from sympy import Matrix, symbols
# Создание символов
a, b, c, d = symbols('a b c d')
# Создание матрицы 2x2
matrix_2x2 = Matrix([[a, b], [c, d]])
print("Матрица 2x2:")
print(matrix_2x2)
Результат работы кода — матрица 2×2:
Матрица 2x2:
Matrix([[a, b], [c, d]])
Сложение, вычитание и умножение матриц
Арифметические операции над матрицами в SymPy можно производить так же, как и над обычными числами, — используя арифметические операторы +, - и *:
from sympy import Matrix, symbols
# Создание символов
a, b, c, d = symbols('a b c d')
# Создание первой матрицы
matrix_2x2 = Matrix([[a, b], [c, d]])
# Создание второй матрицы
matrix_2x2_2 = Matrix([[1, 2], [3, 4]])
# Сложение матриц
sum_matrix = matrix_2x2 + matrix_2x2_2
# Вычитание матриц
diff_matrix = matrix_2x2 − matrix_2x2_2
print("Сумма матриц:")
print(sum_matrix)
print("\nРазность матриц:")
print(diff_matrix)
Вот что выведет программа:
Сумма матриц:
Matrix([[a + 1, b + 2], [c + 3, d + 4]])
Разность матриц:
Matrix([[a - 1, b - 2], [c - 3, d - 4]])
Продолжим наш код:
# Умножение матриц
product_matrix = matrix_2x2 * matrix_2x2_2
print("Произведение матриц:")
print(product_matrix)
Результат выполнения:
Произведение матриц:
Matrix([[a + 3*b, 2*a + 4*b], [c + 3*d, 2*c + 4*d]])Визуализация
Результаты вычислений, полученных с помощью SymPy, можно визуализировать в виде графиков. Однако сама библиотека подходит для этого плохо, так как ориентирована именно на проведение символьных вычислений. Для визуализации результатов обычно используют другие библиотеки, например Matplotlib.

Читайте также:
Построим график функции sin(x)/x.
import sympy as sp
import matplotlib.pyplot as plt
import numpy as np
# Создание символьной переменной
x = sp.symbols('x')
# Определение функции с использованием SymPy
y_expr = sp.sin(x) / x
# Преобразование в функцию, пригодную для использования с библиотекой Matplotlib
y_func = sp.lambdify(x, y_expr, 'numpy')
# Генерация значений x от -10 до 10
x_values = np.linspace(-10, 10, 400)
# Вычисление соответствующих значений y
y_values = y_func(x_values)
# Построение графика с использованием Matplotlib
plt.plot(x_values, y_values, label=r'$\frac{\sin(x)}{x}$')
plt.xlabel('x')
plt.ylabel('y')
plt.title('График функции $y = \\frac{\\sin(x)}{x}$')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.legend()
plt.show()
В этом примере с использованием SymPy создаётся символьная переменная x и определяется функция y = sin(x)/x. Перед тем как построить график с помощью Matplotlib, функцию нужно привести к виду, понятному для библиотеки. Мы сделали это с помощью метода lambdify.
Получили такой график:
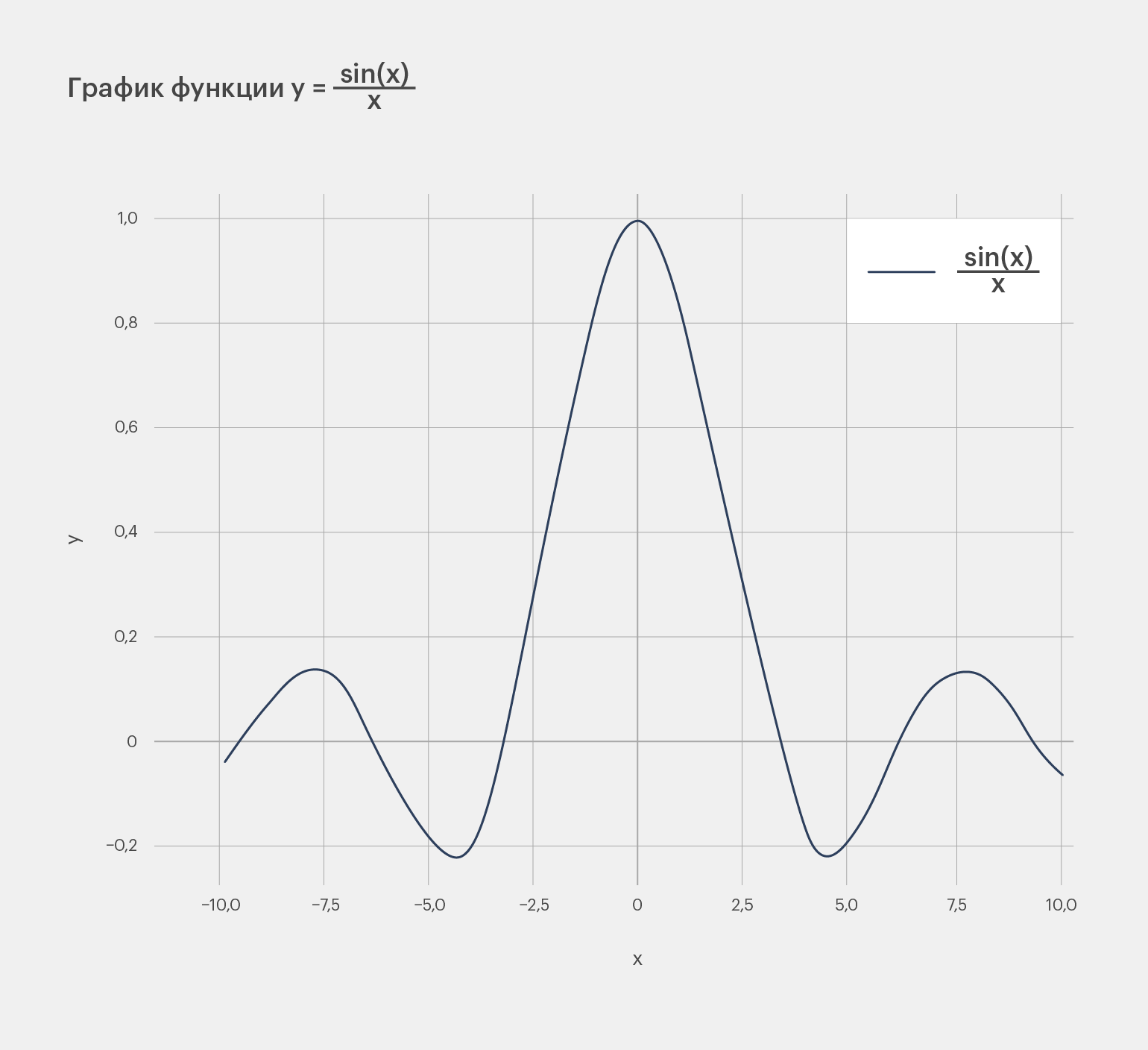
Всё получилось. График функции соответствует математическим ожиданиям.
Что запомнить
Подведём итоги и вспомним, что сегодня узнали:
- Библиотека SymPy используется для символьных вычислений, где формулы — это не только инструменты решения конкретных задач, но также объекты анализа математических структур.
- В SymPy можно работать с символами и переменными, строить выражения, не привязанные к конкретным числам. Это полезно при работе с матрицами, решении уравнений и выполнении математических преобразований.
- Библиотека предоставляет средства для символьного дифференцирования и интегрирования: можно находить производные и интегралы сложных функций, решать дифференциальные уравнения. Это важно при решении физических, инженерных, финансовых и других задач.
- Чтобы визуализировать результаты численных и символьных вычислений, используйте SymPy совместно с библиотеками для построения графиков — Matplotlib, Seaborn и другими.
Python для всех
Вы освоите Python на практике и создадите проекты для портфолио — телеграм-бот, веб-парсер и сайт с нуля. А ещё получите готовый план выхода на удалёнку и фриланс. Спикер — руководитель отдела разработки в «Сбере».
Пройти бесплатно



