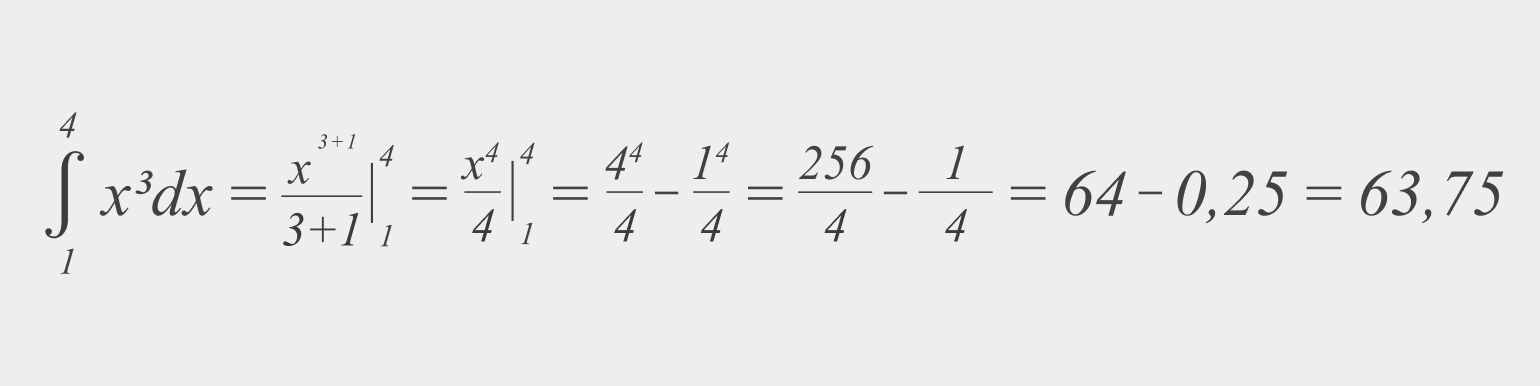Интегралы: всё, что вы хотели знать, без интриг и сложных терминов
Объясняем, почему любой интеграл — это много-много маленьких умножений, и показываем, как его посчитать.


Интегральное исчисление — мудрёный на первый взгляд раздел математического анализа, который оперирует такими понятиями, как «первообразная», «производная», «дифференцирование» и «предел». Оно описывается кучей формул, в которых легко заблудиться, особенно если зайти в тему без должной математической подготовки.
Что такое интеграл в математике
На самом деле в сути интегрирования нет ничего сложного: нужно лишь провести множество операций умножения нескольких слагаемых, а затем сложить результаты этих умножений друг с другом. Идеальный (то есть без погрешностей) интеграл работает с бесконечными величинами.
Если сказать простыми словами, интеграл — это сумма бесконечного количества умножений, проведённых с бесконечно малыми слагаемыми.
Как работает интеграл
В природе практически не существует ничего прямого и постоянного: процессы изменяют свою скорость, а материальные объекты сплошь и рядом неправильной формы. Это сильно затрудняет вычисление и описание реальности, но математики научились с этим справляться.
Представьте, что у вас есть велосипед со спидометром, который не только показывает вашу скорость, но и записывает её в каждый момент времени, а затем выдаёт график вашего движения.
Вы выехали из точки А в точку Б и два часа двигались со средней скоростью 12 км/ч. Так вам казалось, во всяком случае. То есть график вашего движения, по вашему мнению, выглядел как-то так:
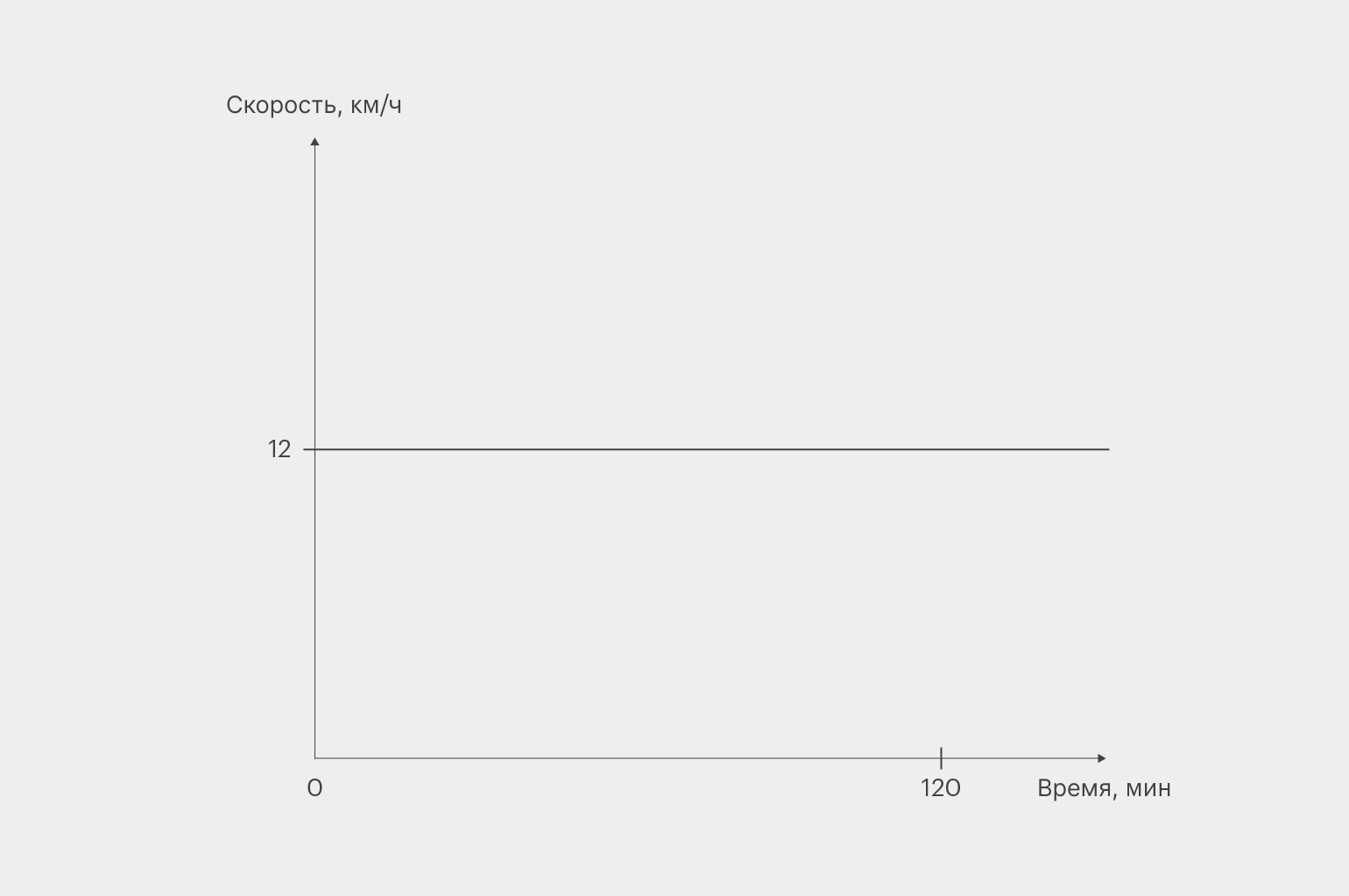
Изображение: Skillbox Media
Но в реальности всё было иначе. Сначала вы колесили не спеша, потом разогнались, потом замедлились на подъёме в горку, затем вообще встали на светофоре, после чего снова пришлось разогнаться. То есть реальный график вашего движения был таким:
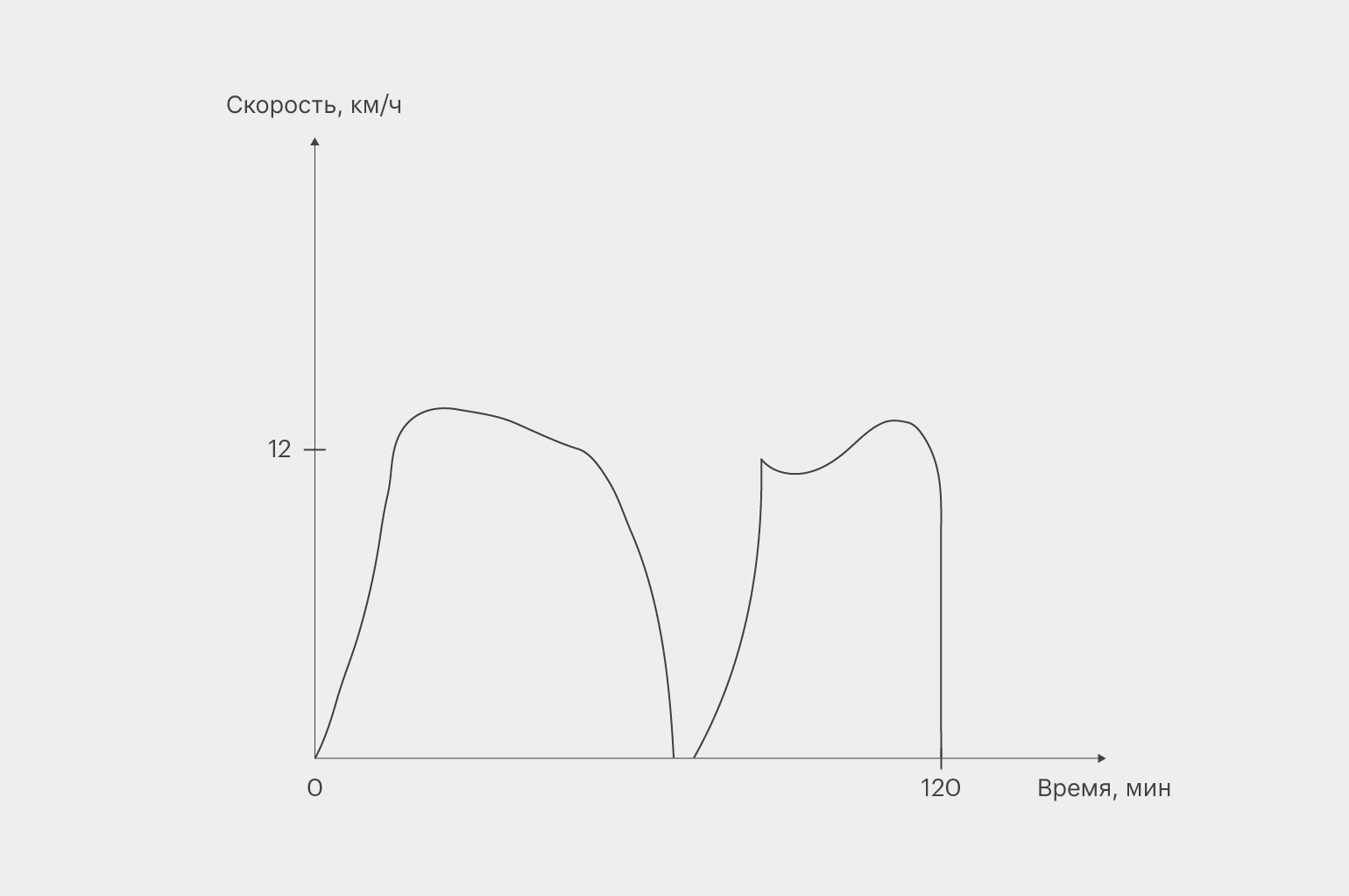
Изображение: Skillbox Media
Скорость менялась, и в разные периоды времени вы проделывали разный путь. Как же посчитать, сколько вы накрутили в итоге?
Очень просто: нужно поделить всё время на равные промежутки — и посчитать, с какой примерно скоростью вы ехали в каждый из них. Возьмём промежутки по 15 минут, умножим их на примерную среднюю скорость, получим расстояние — и представим всё это в таблице.
| Время, мин | Скорость, км/ч | Расстояние, км |
|---|---|---|
| 0–15 | ~7 | ~1,75 |
| 15–30 | ~13 | ~3,25 |
| 30–45 | ~12 | ~3 |
| 45–60 | ~8 | ~2 |
| 60–75 | ~4 | ~1 |
| 75–90 | ~7 | ~1,75 |
| 90–105 | ~12 | ~3 |
| 105–120 | ~11 | ~2,75 |
Теперь сложим все расстояния и получим приблизительно 18,5 км. Но это всё ещё не точный результат: скорость-то мы оценивали примерно.
Чтобы посчитать точнее, нужно взять как можно большее количество промежутков — по минуте, секунде, наносекунде и так далее. Чем короче будет каждый промежуток, тем ближе к реальности окажется результат.
В идеале наш график можно поделить на число промежутков, стремящееся к бесконечности, а размер каждого из них будет стремиться, соответственно, к нулю. Затем произвести умножение во всех промежутках и сложить результаты — в общем, сделать то же, что и раньше. Только табличка получится безразмерная. Это и есть интеграл нашей функции, который математически, если кто не помнит, записывается так:
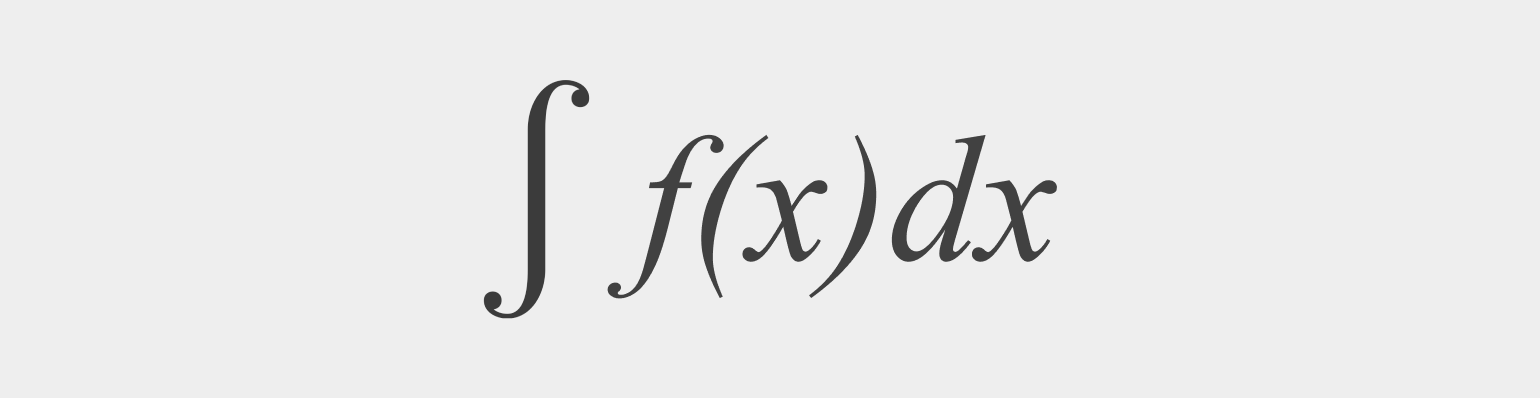
∫ — значок интеграла. Выбран неслучайно: так как интеграл представляет собой сумму, то и обозначается вытянутой буквой S.
f(x) — это функция, которую мы интегрируем. В нашем примере мы задали функцию вручную, а не формулой, но математики работают именно с формулами.
dx — это обозначение того, что каждый промежуток является бесконечно малой величиной. Читается как «дельта икс».
При чём здесь дифференциал
У интегрирования есть ещё один математический смысл. Это операция, обратная дифференцированию. Давайте разберёмся, что это значит.
Представьте, что вы выпускаете в космосе аппарат, который удаляется от вас по формуле y = x2, где y — расстояние от вас в километрах, а x — время в часах. Причём x может принимать только положительные значения.
Вот график движения этого аппарата:
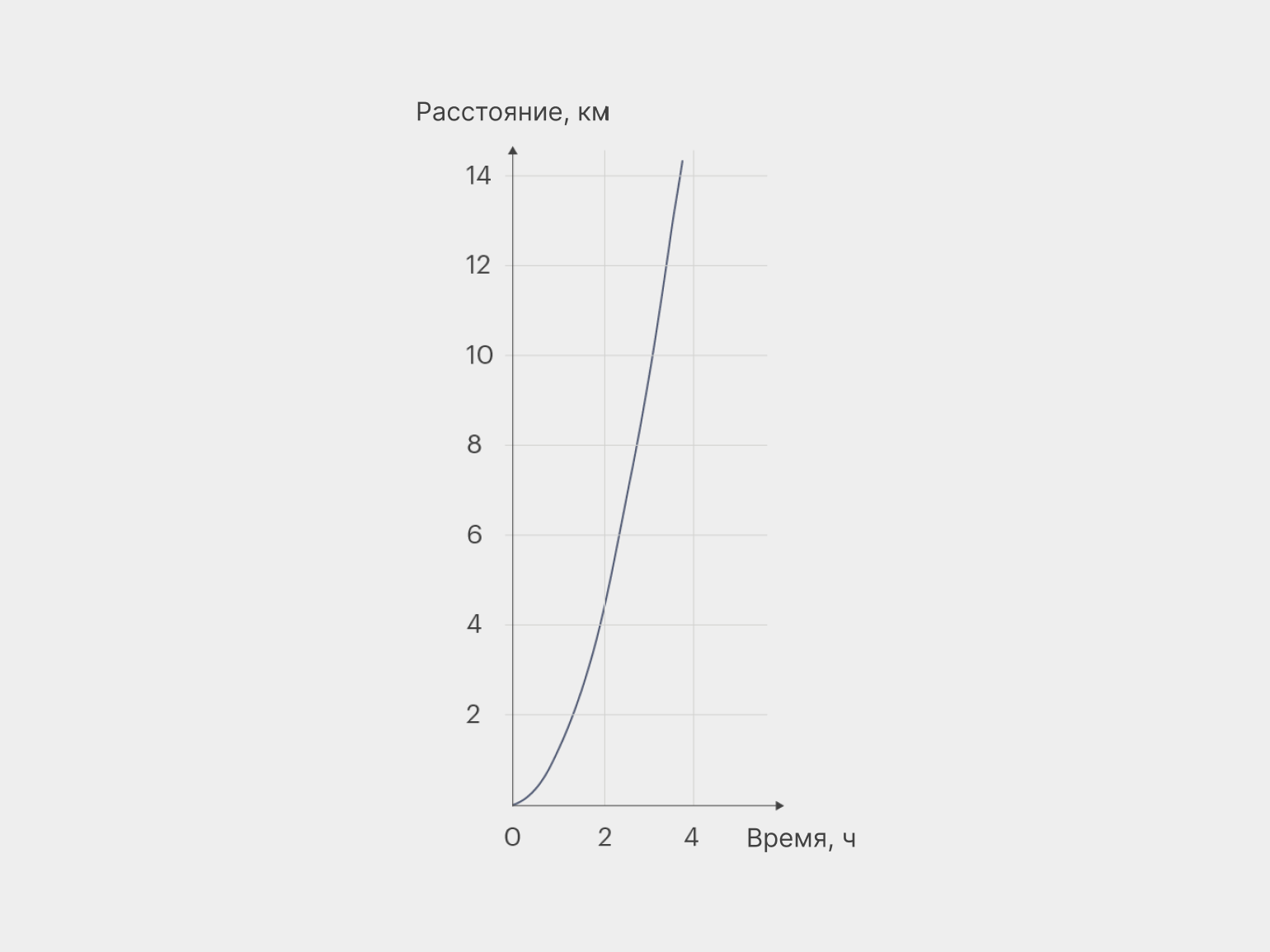
Наша функция растёт неравномерно: скорость её роста увеличивается, причём по определённому принципу.
Чтобы найти эту скорость, или, математически выражаясь, производную нашей функции, придумали дифференцирование. Производной от функции f(x2) будет F(2x). Физически она будет показывать не положение аппарата в пространстве, а скорость, с которой движется аппарат:
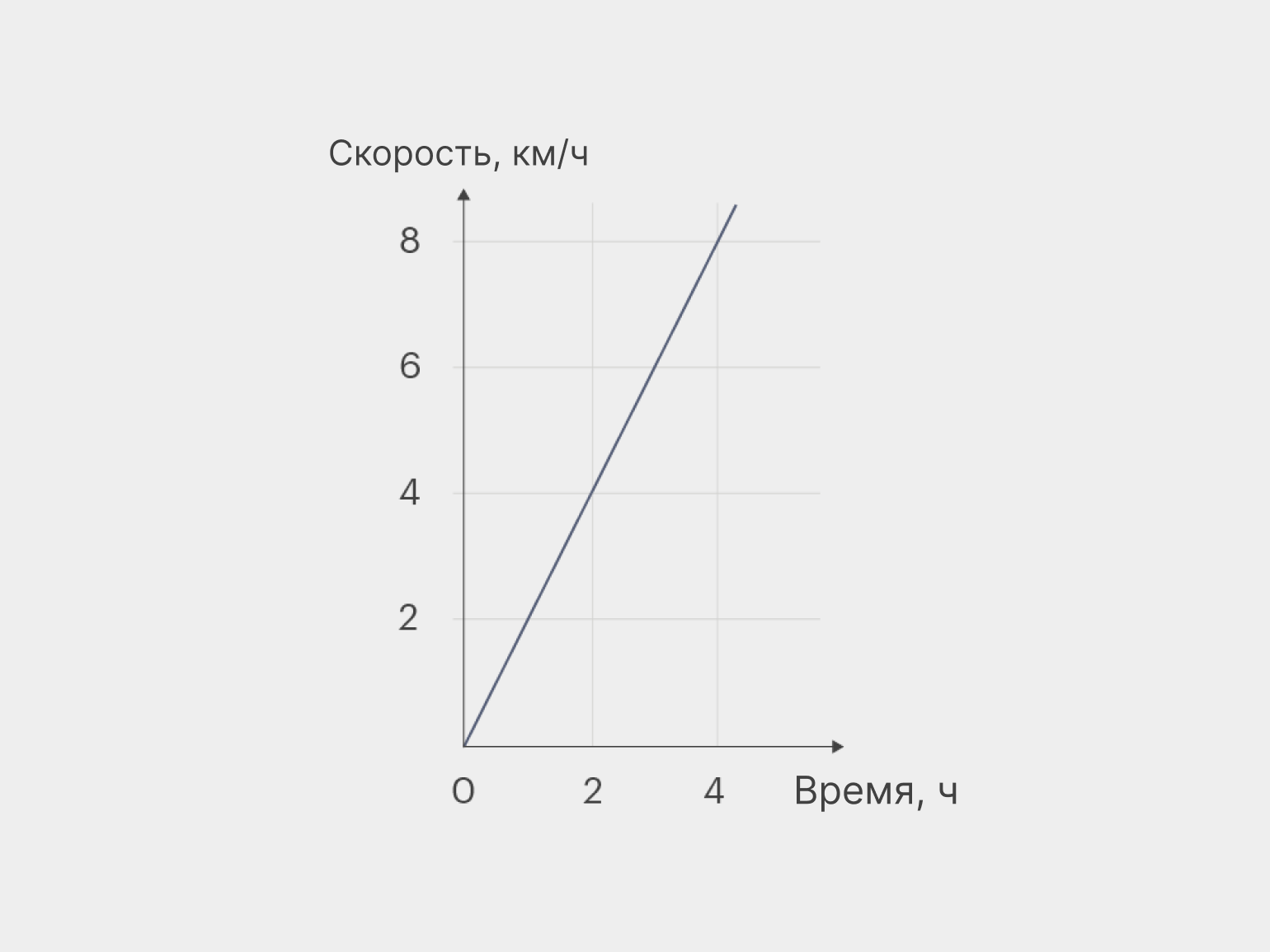
Изображение: Skillbox Media
Сравните саму функцию и её производную (то есть скорость изменения этой функции). Она растёт — её производная принимает положительные значения. Она начинает расти быстрее — её производная принимает более высокие значения.
Чтобы лучше понять смысл производной, посмотрите на графики функций и их производных и попробуйте понять связь между ними:
Изображение: Skillbox Media
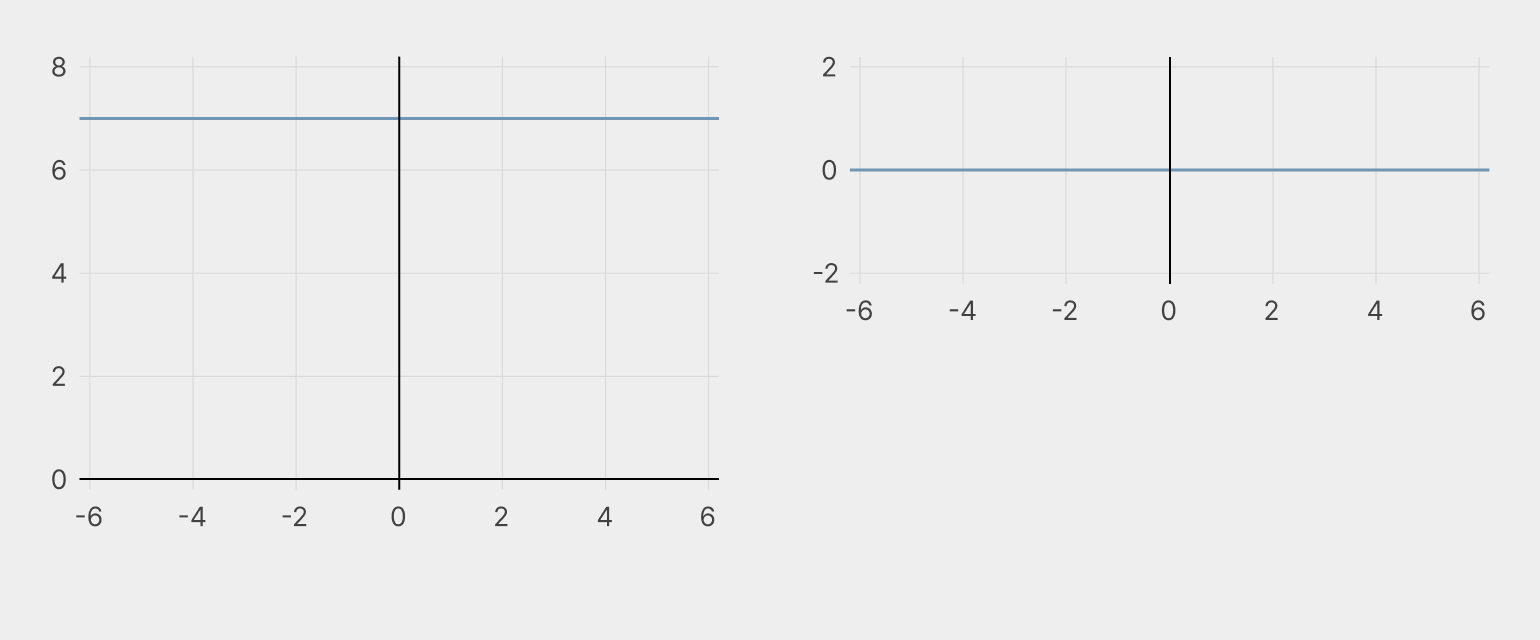
Слева — y = 8, справа — производная y = 0. Так как функция не растёт и не убывает, то и её производная отражает отсутствие изменений в левом графике.
Изображение: Skillbox Media
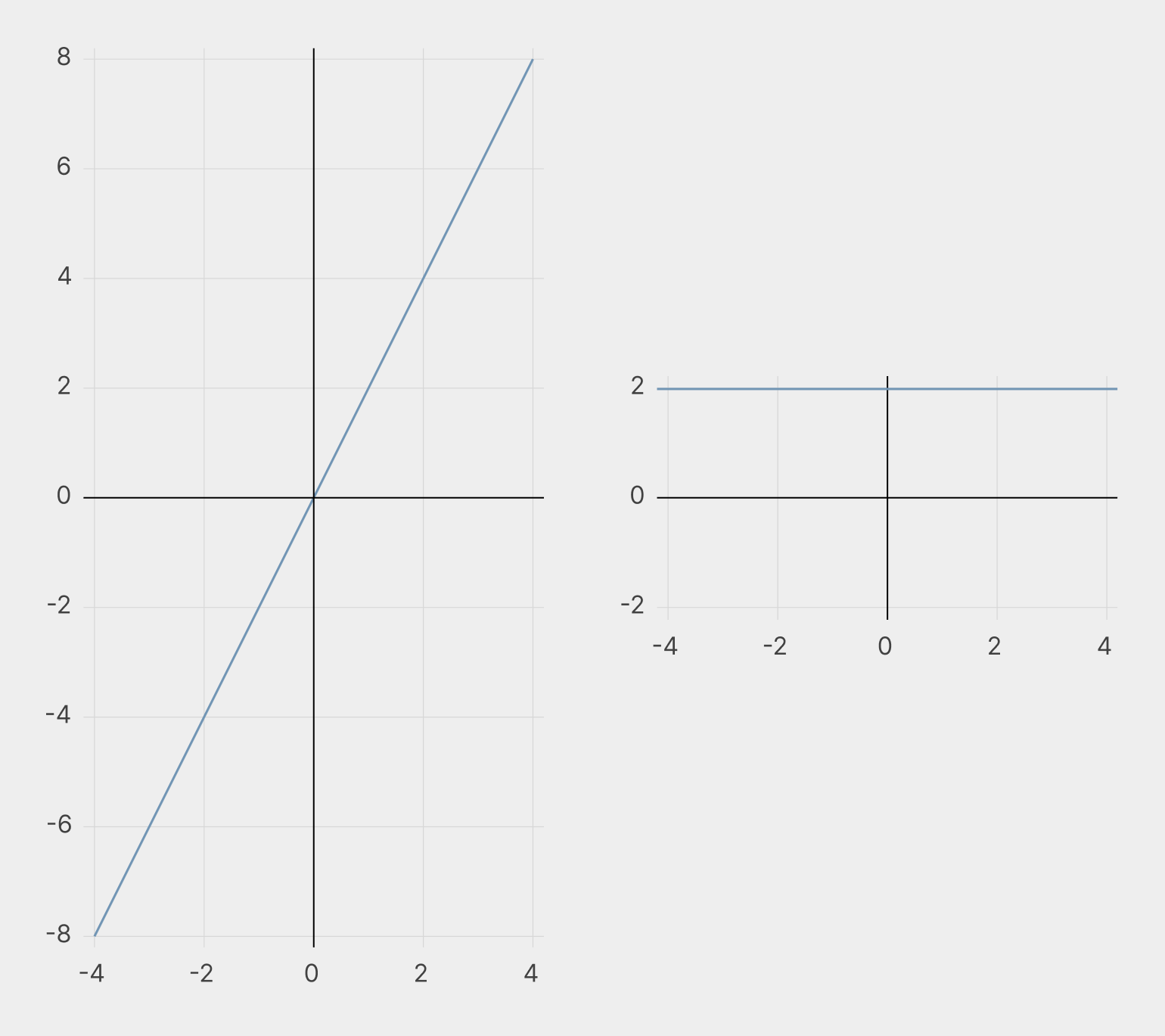
Слева — y = 2x, справа — производная y = 2. Функция равномерно растёт в течение всего своего существования. Её производная отражает наличие роста и то, что этот рост неизменен: за каждый шаг x к функции всегда прибавляются два шага y.
Изображение: Skillbox Media
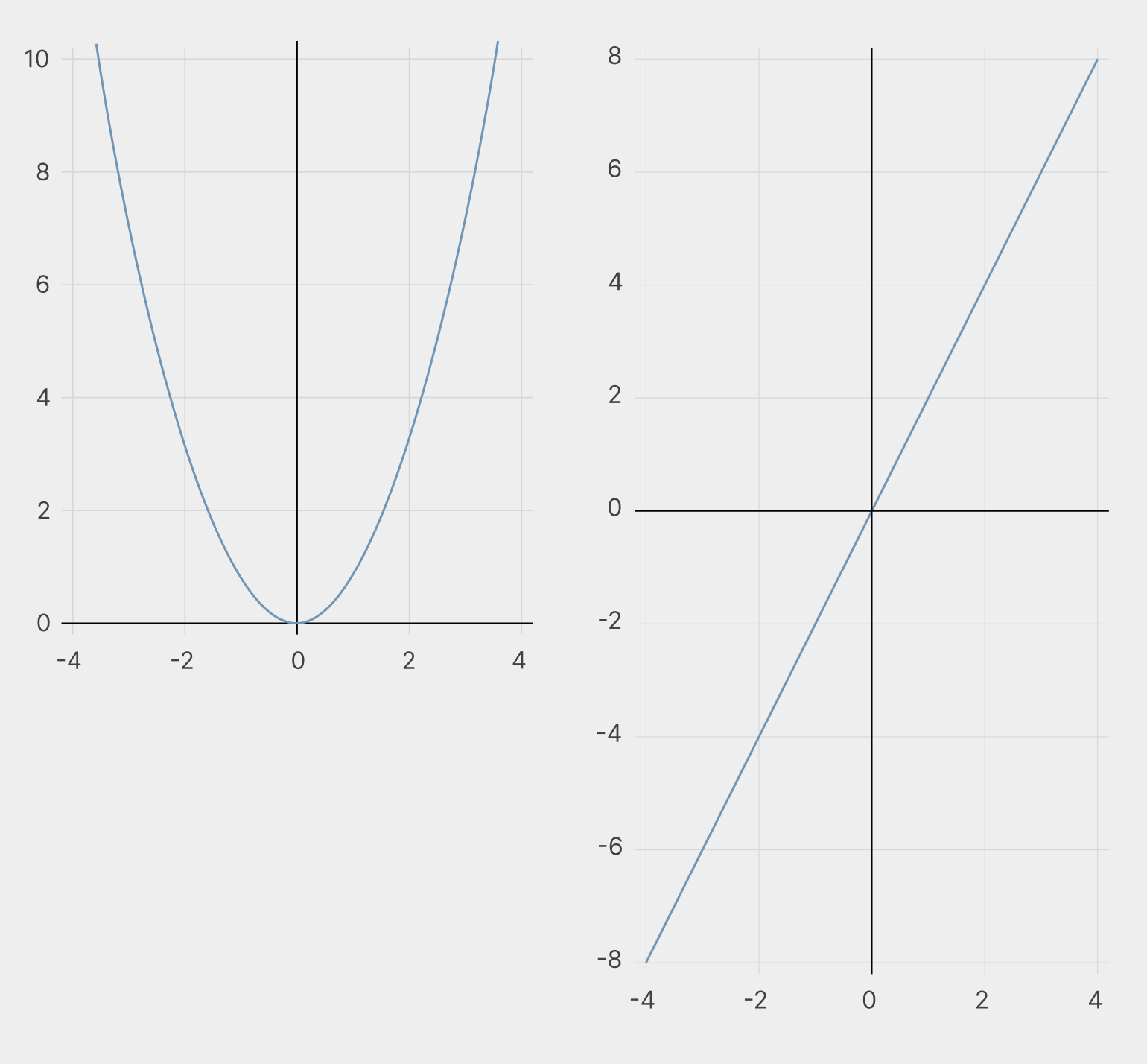
Слева — y = x2, справа — производная y = 2x. Чтобы лучше понять связь, рассмотрим графики по частям.
На промежутке от минус бесконечности до нуля функция убывает. Следовательно, её производная принимает отрицательные значения.
Чем дальше, тем медленнее убывает левый график. На промежутке x от −3 до −2 он уменьшается с 9 до 4 — сразу на пять делений. А на промежутке от −2 до −1 уменьшается с 4 до 2 — всего на два деления. Так и производная, приближаясь к нулю, показывает, что функция убывает всё медленнее и медленнее.
В точке x = 0 функция не растёт и не убывает. Следовательно, в этой точке её производная равна нулю.
На промежутке от нуля до плюс бесконечности левый график растёт. Следовательно, производная принимает положительные значения.
Чем дальше, тем рост быстрее — по аналогии с предыдущим промежутком. Вместе с тем и производная увеличивает свои значения и этим показывает всё ускоряющийся рост функции. Всё это нужно понять, потому что интегрирование — это операция, обратная дифференцированию.
А теперь вернёмся к нашим интегралам. Если при дифференцировании мы ищем производную и превращаем левый график в правый, то при интегрировании поступаем наоборот: ищем первообразную и превращаем правый график в левый.
Вернёмся к аппарату, который мы запустили в космос. Мы знали расстояние, на котором он был от нас в каждый момент времени, и с помощью дифференцирования построили график его скорости.
Если же мы знаем скорость аппарата в каждый момент времени, то можем сделать наоборот и с помощью интегрирования построить график его перемещения.
Что такое неопределённый интеграл
Итак, мы выяснили, что с помощью интегралов можем воспроизвести функцию, зная только её производную. Такая восстановленная функция называется первообразной, а интеграл, который её ищет, — неопределённым. Для него выбрали такое имя, потому что он представляет собой не конкретное число, а целую функцию.
У неопределённого интегрирования есть интересная особенность — оно возвращает не одну первообразную, а целое их семейство.
Возьмём три первообразные: f(2x), f(2x + 5) и f(2x − 5). Вот их графики.
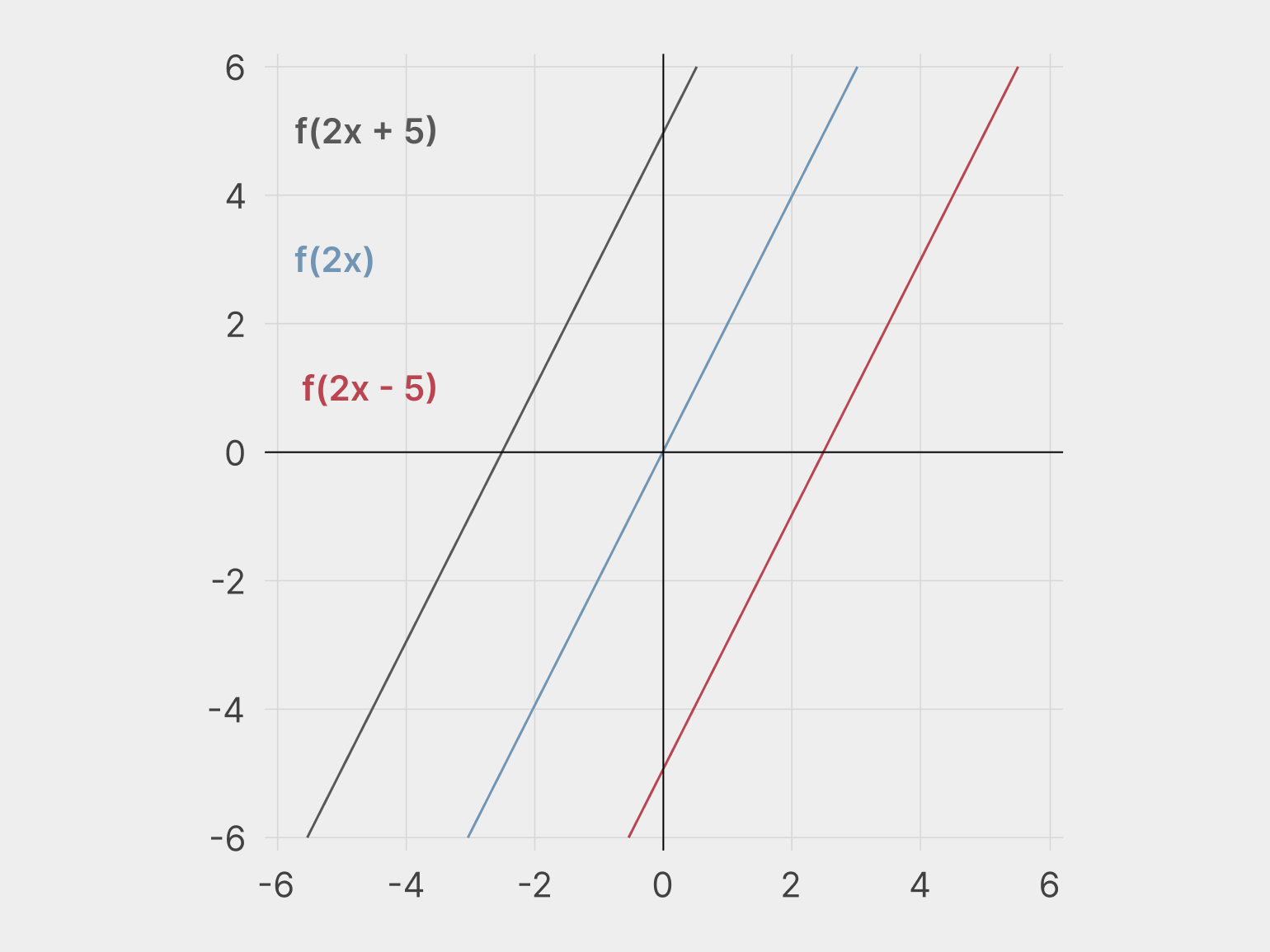
Теперь продифференцируем функции и найдём производную для каждой из них. Во всех трёх случаях получается F(2), то есть y = 2.
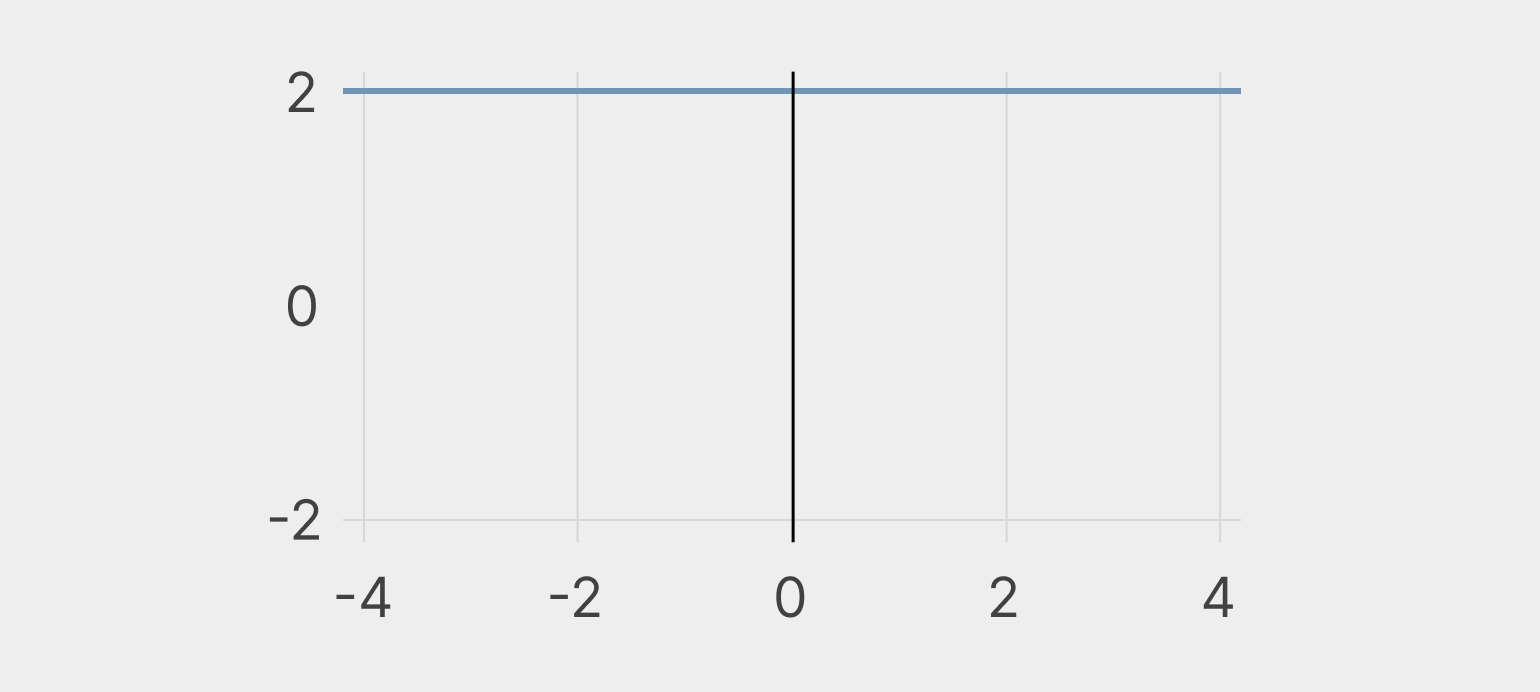
Так получается, потому что каждая из этих функция растёт с одинаковой скоростью: за один шаг в «иксе» они прибавляют два шага в «игреке». Следовательно, и производная у них одна и та же.
Интегрирование — обратная операция. Когда мы берём интеграл от F(2), то можем получить и f(2x), и f(2x + 5), и f(2x − 5), бесконечное количество других функций того же типа. Это дополнительное число называется произвольной постоянной.
Поэтому, когда мы берём неопределённый интеграл, то указываем в результате эту произвольную постоянную: f(2x + C).
В общем виде неопределённый интеграл выглядит так:
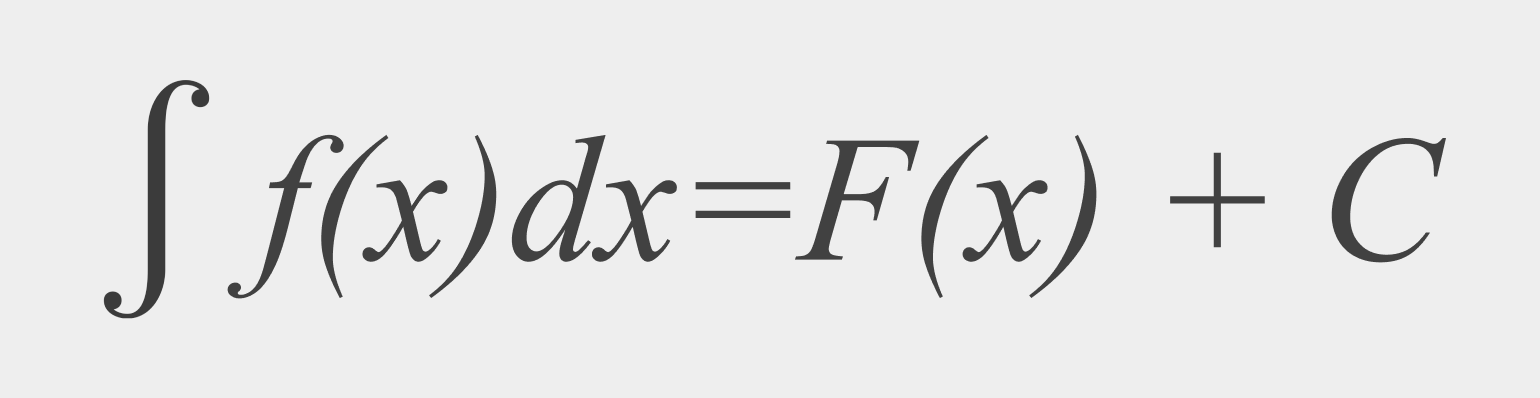
Что такое определённый интеграл
Определённый интеграл отличается от неопределённого тем, что его результатом является не формула (семейство первообразных), а конкретное число.
Когда мы считали, сколько проехали на велосипеде за два часа, то брали именно определённый интеграл. Его запись отличается от записи неопределённого интеграла и выглядит так:
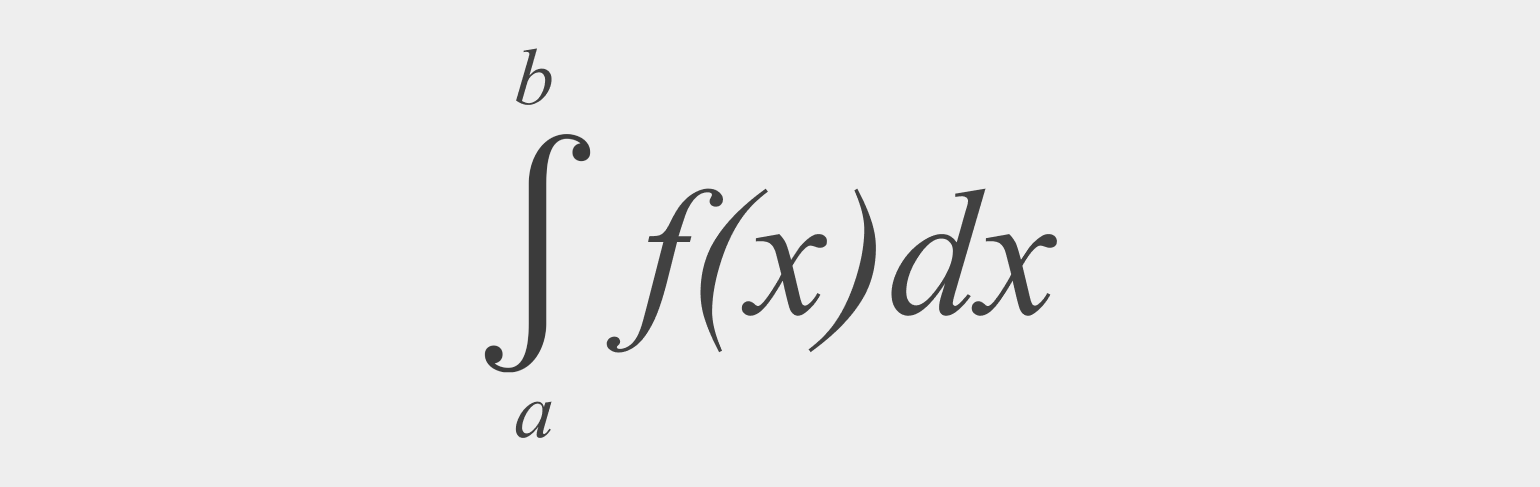
a здесь обозначает начало интегрируемого промежутка, b — его окончание. Таким образом, если мы берём интеграл:
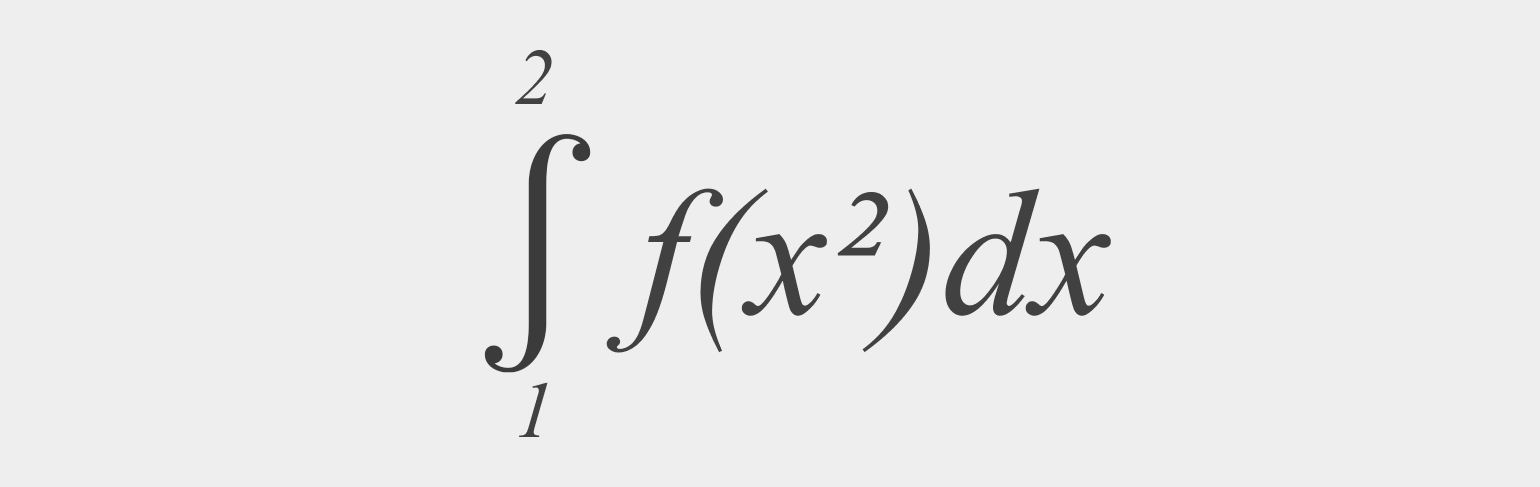
То нас интересует только вот этот кусок параболы:
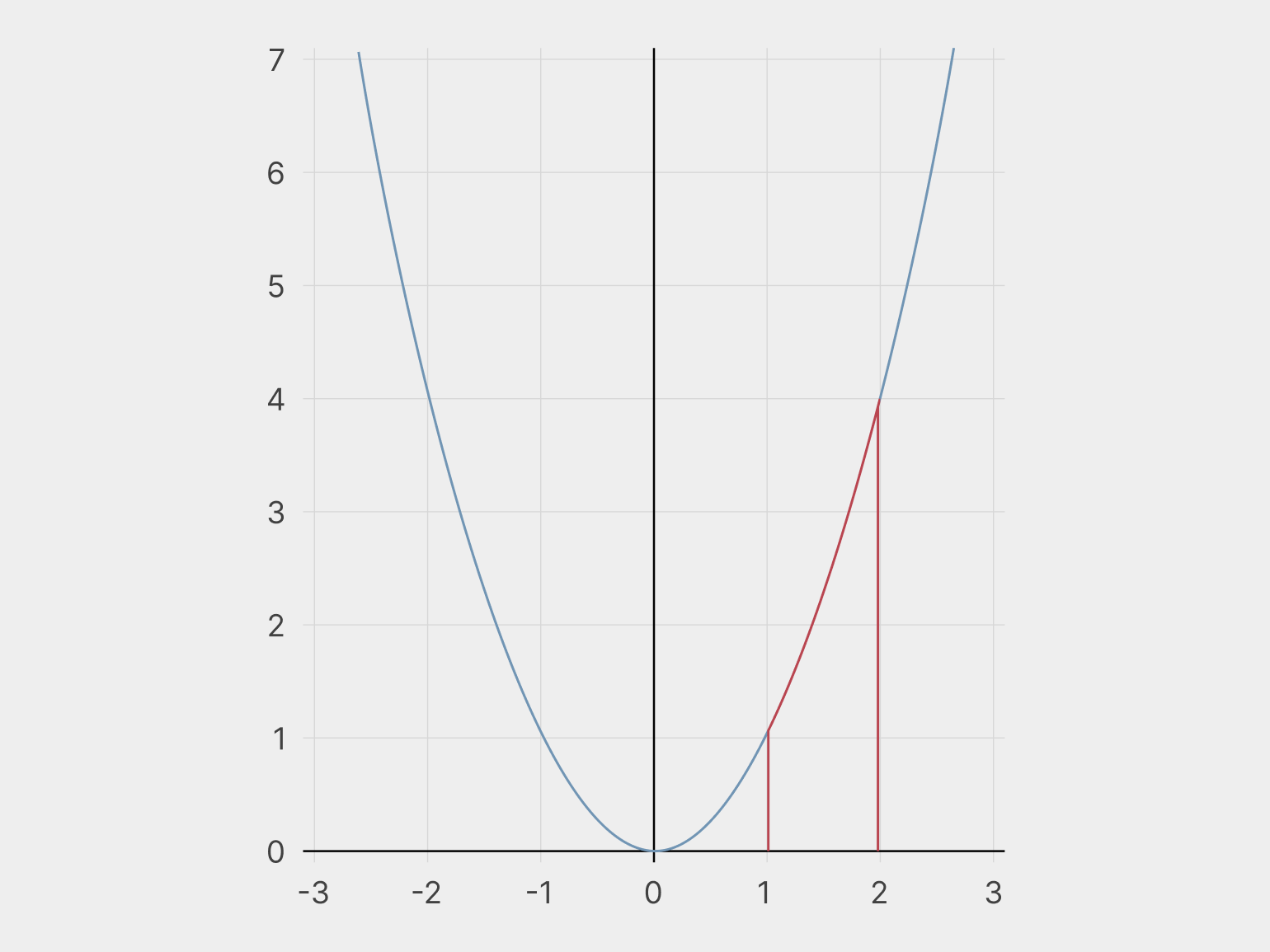
Наши красные линии вам ничего не напоминают? Это же криволинейная трапеция! А так как интеграл представляет собой сумму маленьких умножений x на y в каждой возможной точке, то в результате интегрирования у нас получается площадь красной фигуры.
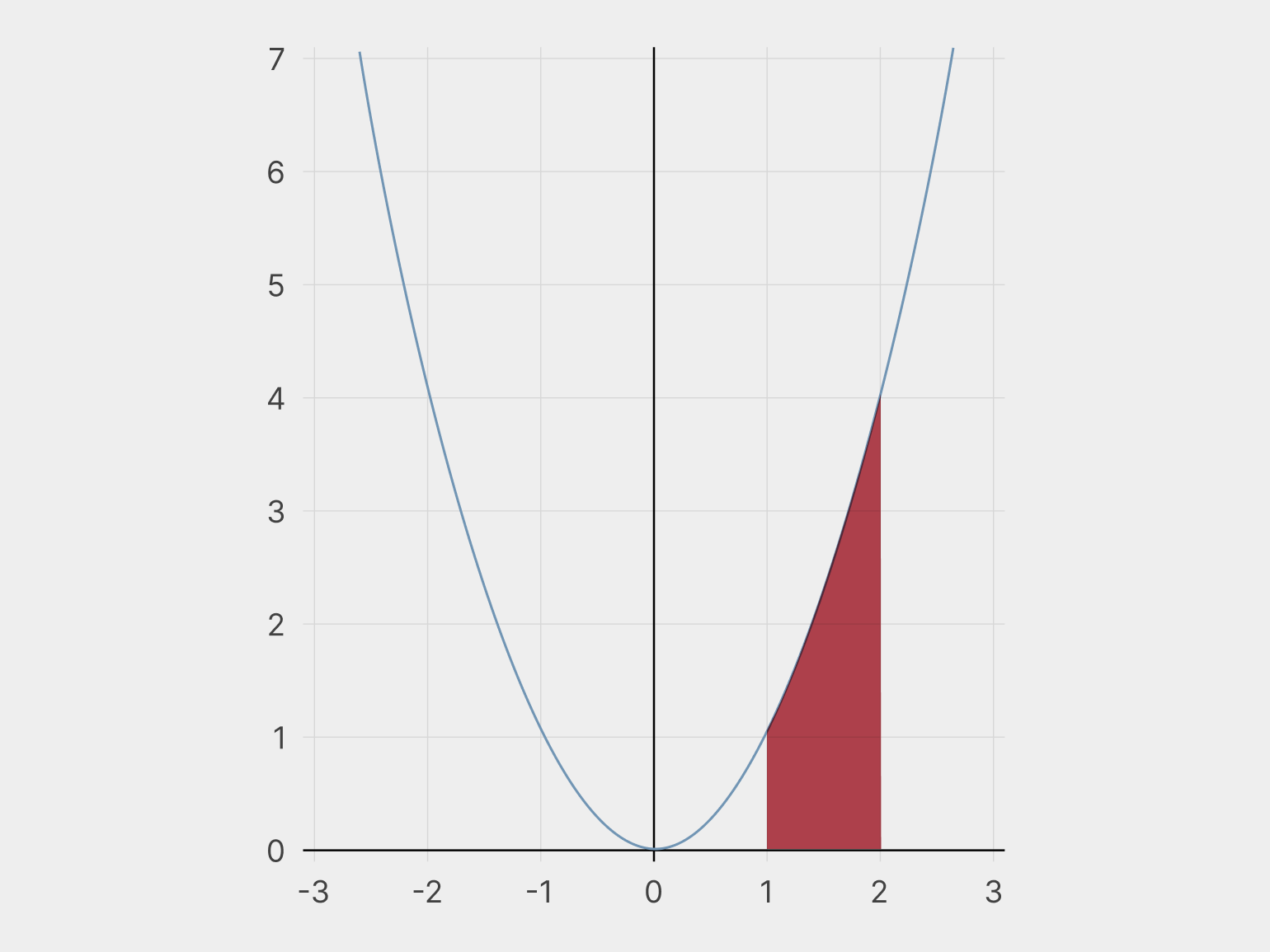
Именно поэтому интеграл часто описывают как «площадь фигуры под кривой» — это одно из его геометрических проявлений.
Как считать интегралы
Теперь давайте посмотрим, как посчитать интеграл
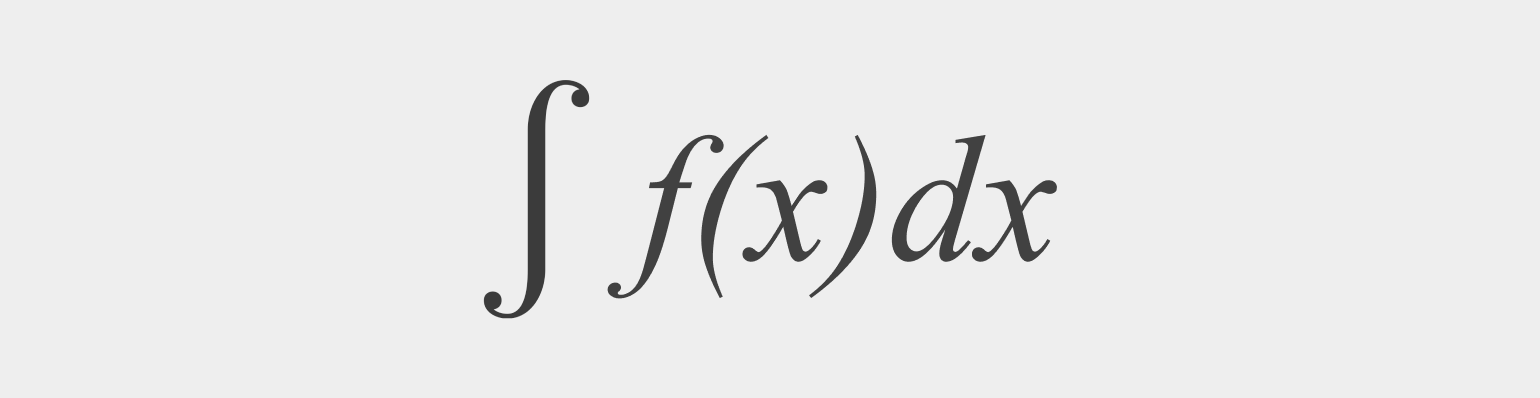
Если интеграл сложный, то сначала его нужно преобразовать, пользуясь методами интегрирования. Этих методов не очень много, но они сложные и комплексные, поэтому мы не рассматриваем их в этой статье.
Примечание. Интегрировать можно не каждую функцию. Это возможно только в тех случаях, когда она определена и непрерывна в области интегрирования.
После того как подынтегральная функция приведена в элементарный вид, нужно найти её первообразную. Чтобы сделать это, следует воспользоваться таблицей неопределённых интегралов.
Вот список основных и самых простых (но далеко не всех) интегралов:
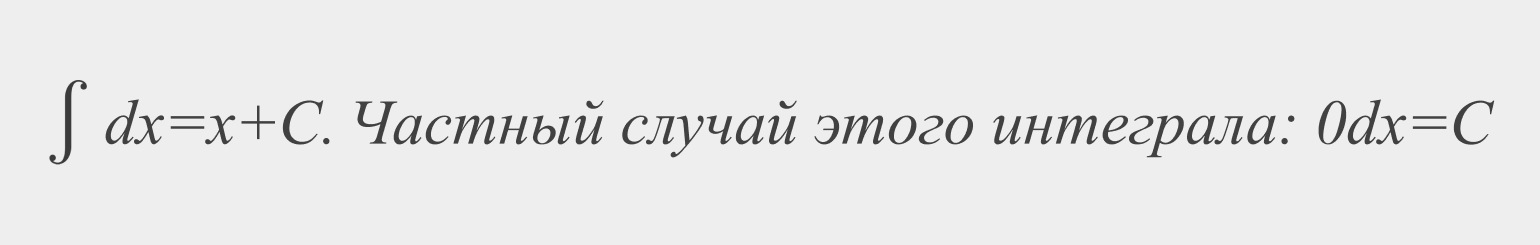







Если вы считали неопределённый интеграл, то вуаля: подставляете значения в формулу, и ответ готов — очень просто. Если же вы ищете определённый интеграл, нужно воспользоваться формулой Ньютона — Лейбница.
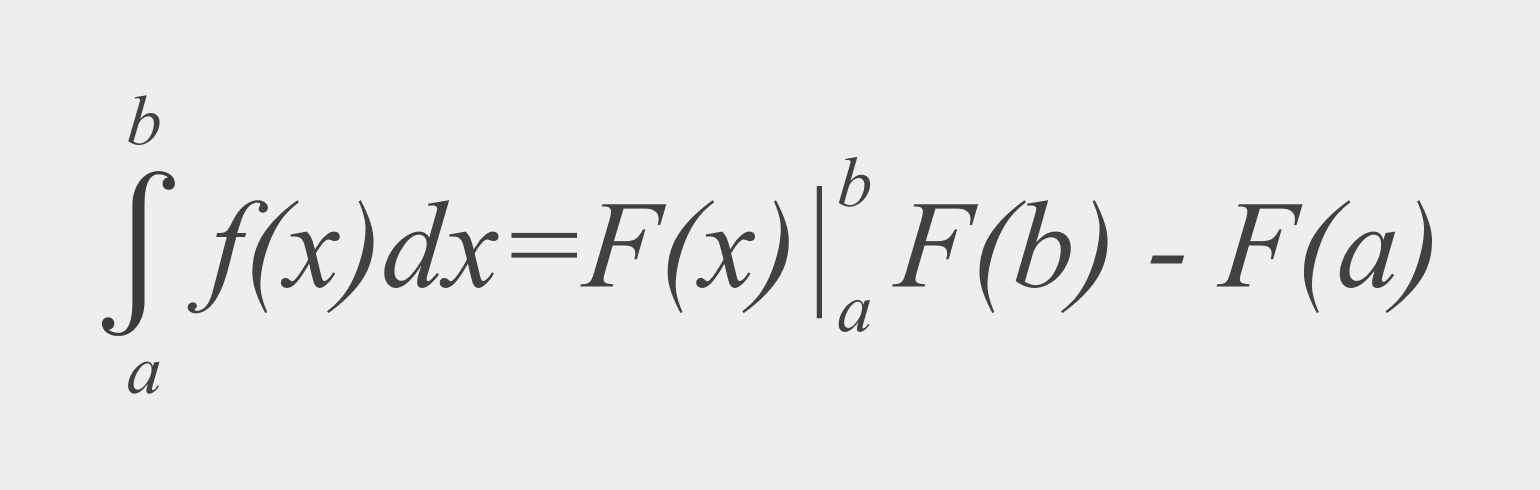
Как видим, для нахождения определённого интеграла необходимо провести два преобразования.
Сначала, как и в случае с неопределённым интегралом, мы находим первообразную F (x). Константа C в этом случае не добавляется.

Этот символ значит, что мы работаем со значениями этой первообразной от a до b.
Затем мы должны подставить значения a и b в найденную первообразную, посчитать результат и найти разность этих результатов. Это и будет определённый интеграл.
Примеры решения интегралов
Чтобы было нагляднее и понятнее, закрепим алгоритм интегрирования несколькими простыми примерами.
Пример 1
Найдите неопределённый интеграл:
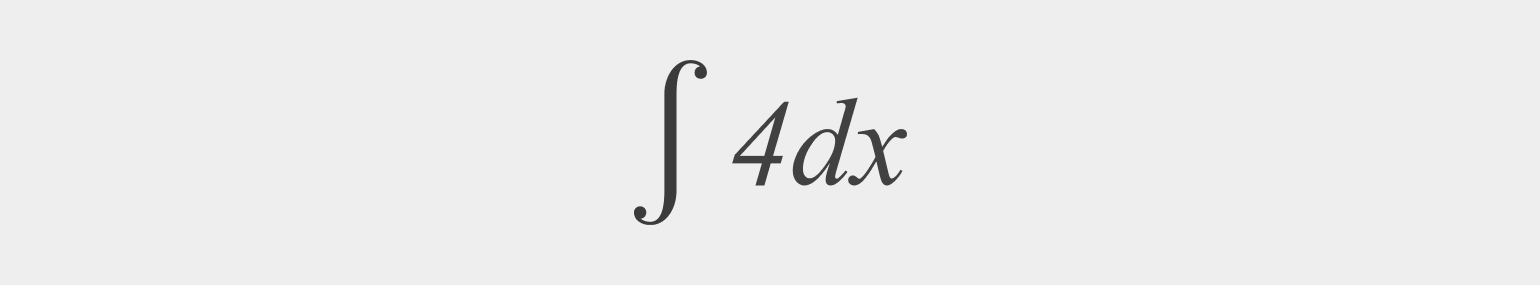
Решение
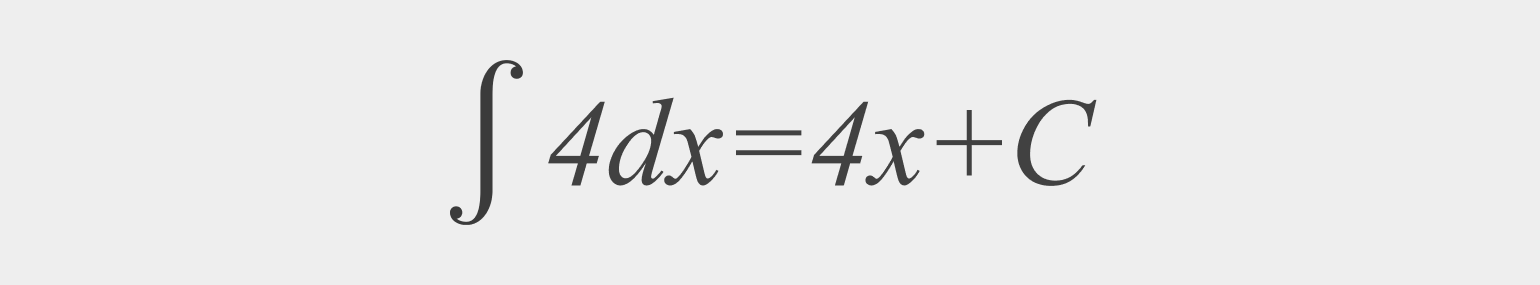
Пример 2
Найдите определённый интеграл:
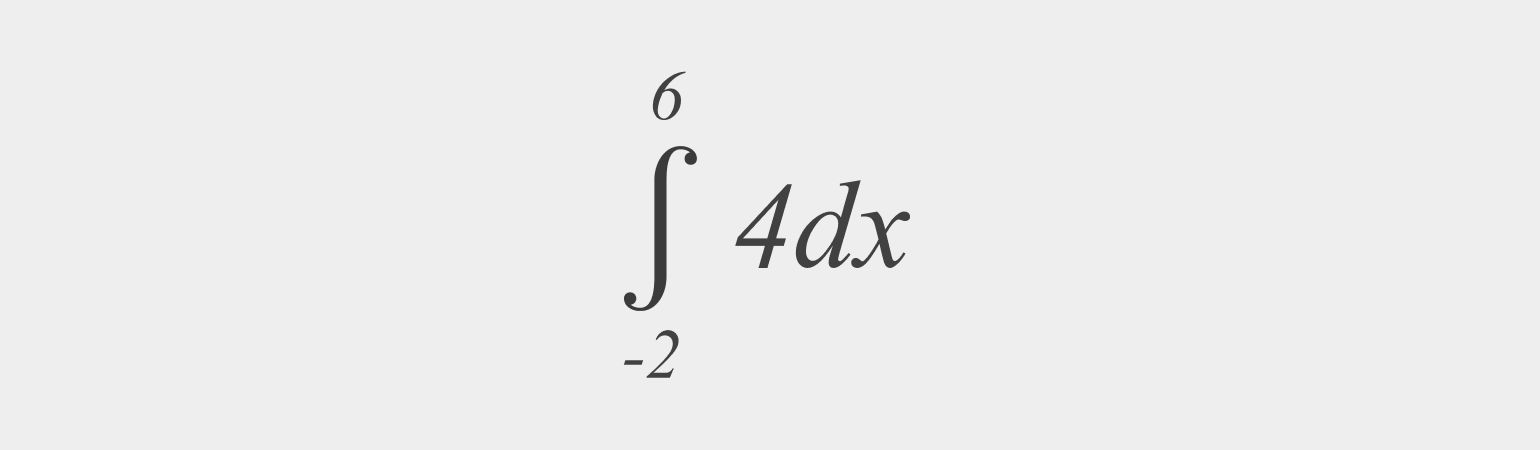
Решение

Пример 3
Найдите неопределённый интеграл:
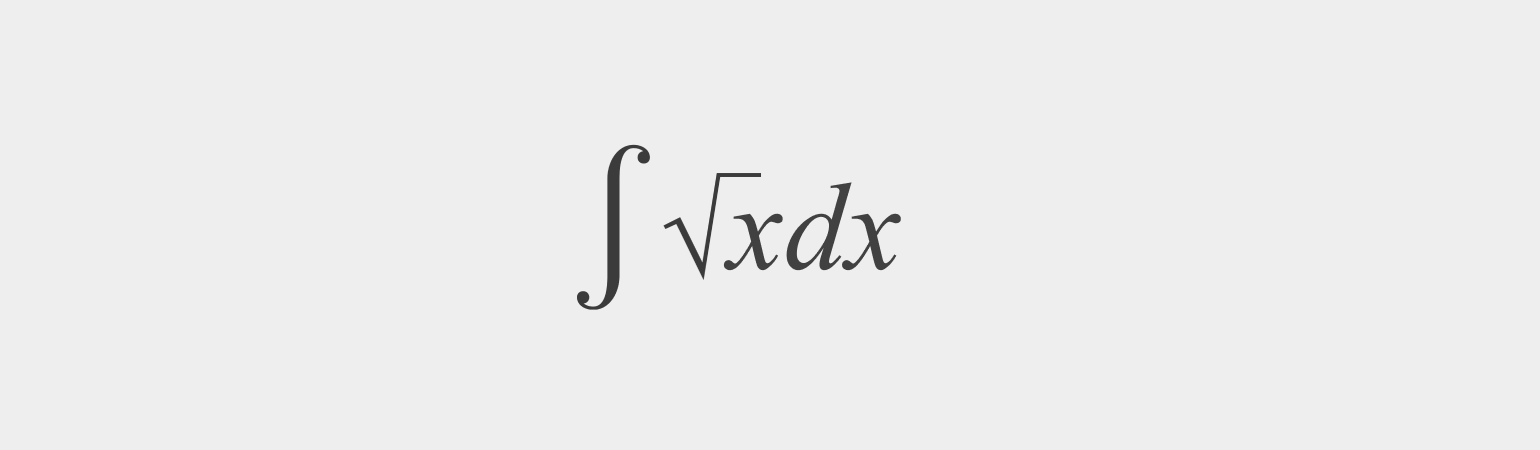
Решение
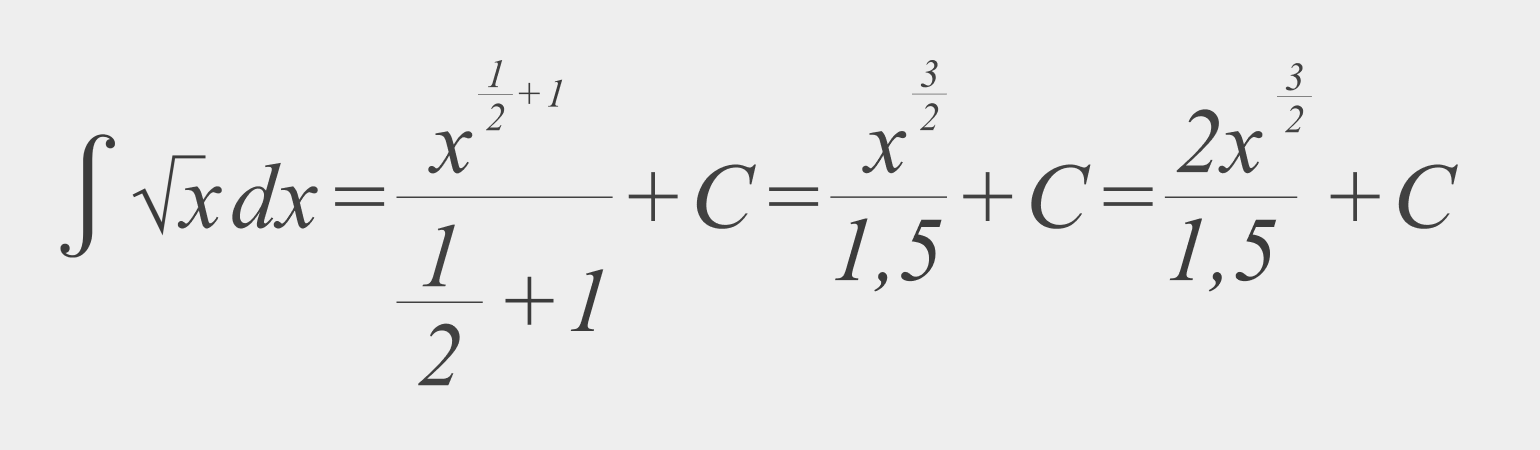
Обратите внимание, что если построить график функции и её первообразной, то в обоих случаях x будет принимать значения от нуля до плюс бесконечности.
Пример 4
Найдите определённый интеграл:
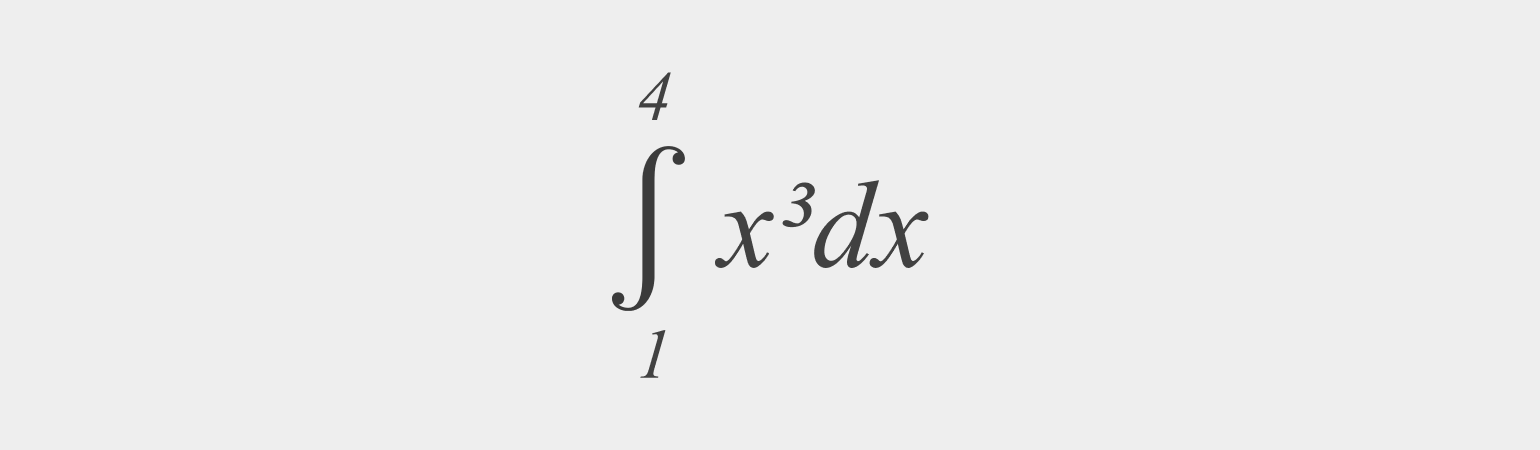
Решение