Запутанная задача про поп-ит
Считаем остаток от деления с репетитором Анной Никитиной.



Анна Никитина
Преподаватель математики, автор YouTube-канала «Математика с Аней» и соавтор учебников и методических рекомендаций к учебникам по математике.
Анна готовит учеников к ЕГЭ в школе «Топскул» и консультирует онлайн-школы по вопросам эффективного обучения.
Условие
Сыграем в поп-ит с 24 пузыриками. Вот такой:

Правила игры:
- Участвуют два игрока, которые ходят по очереди. Вы начинаете.
- За один ход можно лопнуть 1, 2 или 3 пузырика.
- В начале игры все 24 пузырика целые.
- Проигрывает тот, кто лопнет последний пузырик.
- Никто из игроков не поддаётся, каждый считает ходы и старается выиграть.
Придумайте стратегию, которая приведёт вас к победе при любых ходах соперника.
Задание со звёздочкой ★: вы ходите вторым. Придумайте победную стратегию, если такая существует.
Задание с двумя звёздочками ★★: пузыриков в поп-ите не 24, а любое количество. Попробуйте составить выигрышную стратегию.
Подсказка
Начните рассуждать с конца и продумайте ходы, если на поп-ите останется 1, 2, 3, 4 или более свободных пузыриков. Так вы рассчитаете, сколько пузыриков нужно лопать, чтобы при любых ходах соперника удержать его в проигрышной позиции.
Решение
Шаг №1
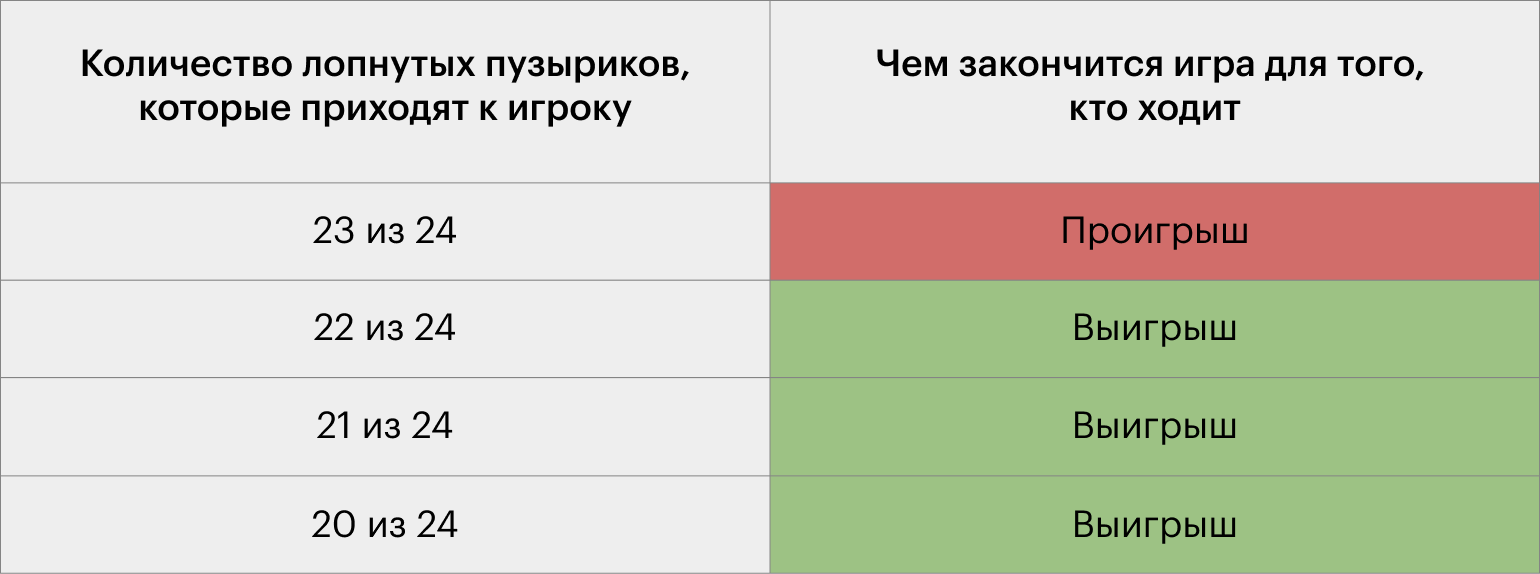
Представим, что мы лопнули 23 из 24 пузыриков и оставили сопернику один ход. В этом случае соперник проиграет, поскольку ему нужно лопнуть последний пузырик.
Теперь лопаем 22 из 24 пузыриков. Здесь выиграет соперник: он лопнет 1 пузырик и оставит нам последний ход. Ситуация повторится, если мы лопнем 21 из 24 или 20 из 24 пузыриков, — соперник лопнет 2 или 3 пузырика и мы будем заканчивать игру.
Шаг №2
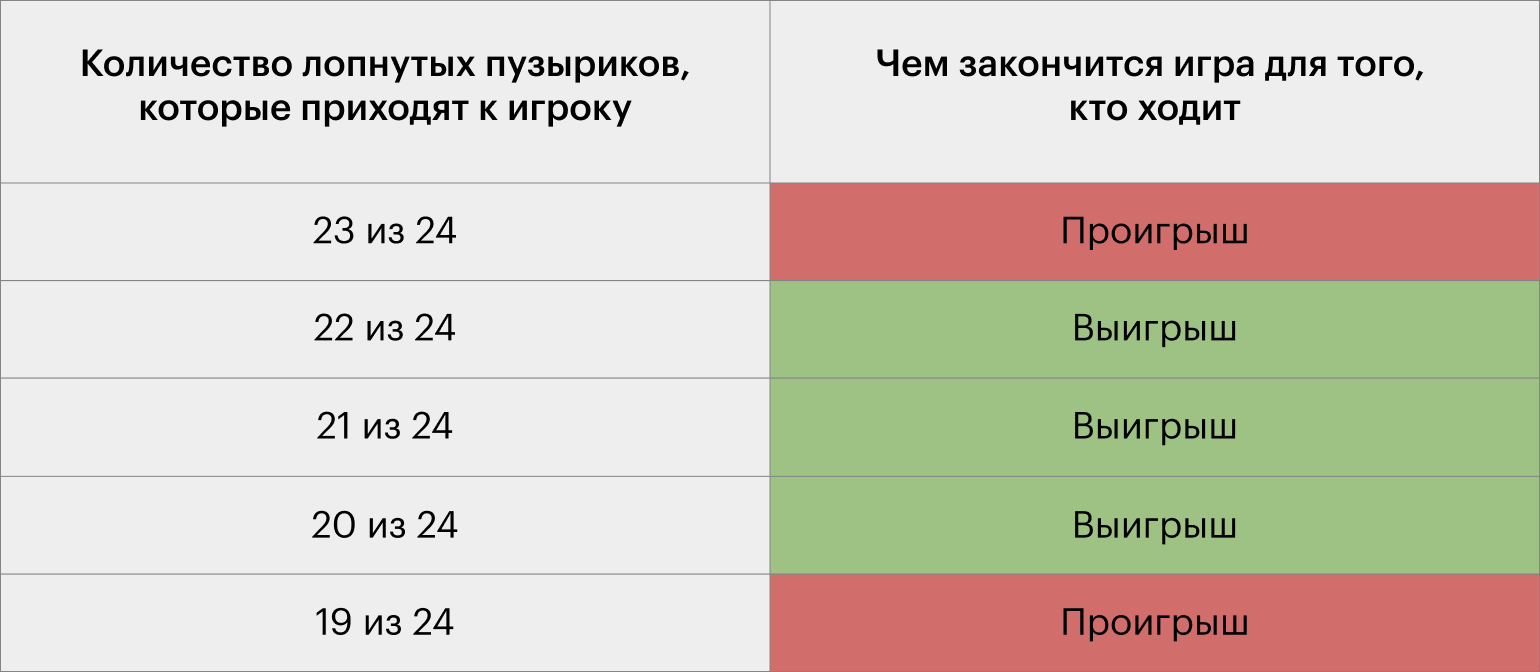
Продолжаем и лопаем 19 из 24 пузыриков. У соперника остаётся 5 свободных пузыриков и 3 варианта хода на выбор: можно лопнуть 1, 2 или 3 пузырика. Для него это проигрышная позиция, поскольку следующим ходом мы завершим игру и победим:
- Если соперник лопнет 1 пузырик, то мы получим поп-ит с 20 лопнутыми и 4 свободными пузыриками. Наш ход: лопаем 3 пузырика.
- Если соперник лопнет 2 пузырика, то в поп-ите будет 21 лопнутый и 3 свободных пузырика. Наш ход: лопаем 2 пузырика.
- Если соперник лопнет 3 пузырика, то в поп-ите останется 22 лопнутых и 2 свободных пузырика. Наш ход: лопаем 1 пузырик.
Во всех перечисленных случаях мы передаём сопернику последний ход и оставляем его с одним свободным пузыриком — создаём условие, при котором он проиграет.
Шаг №3
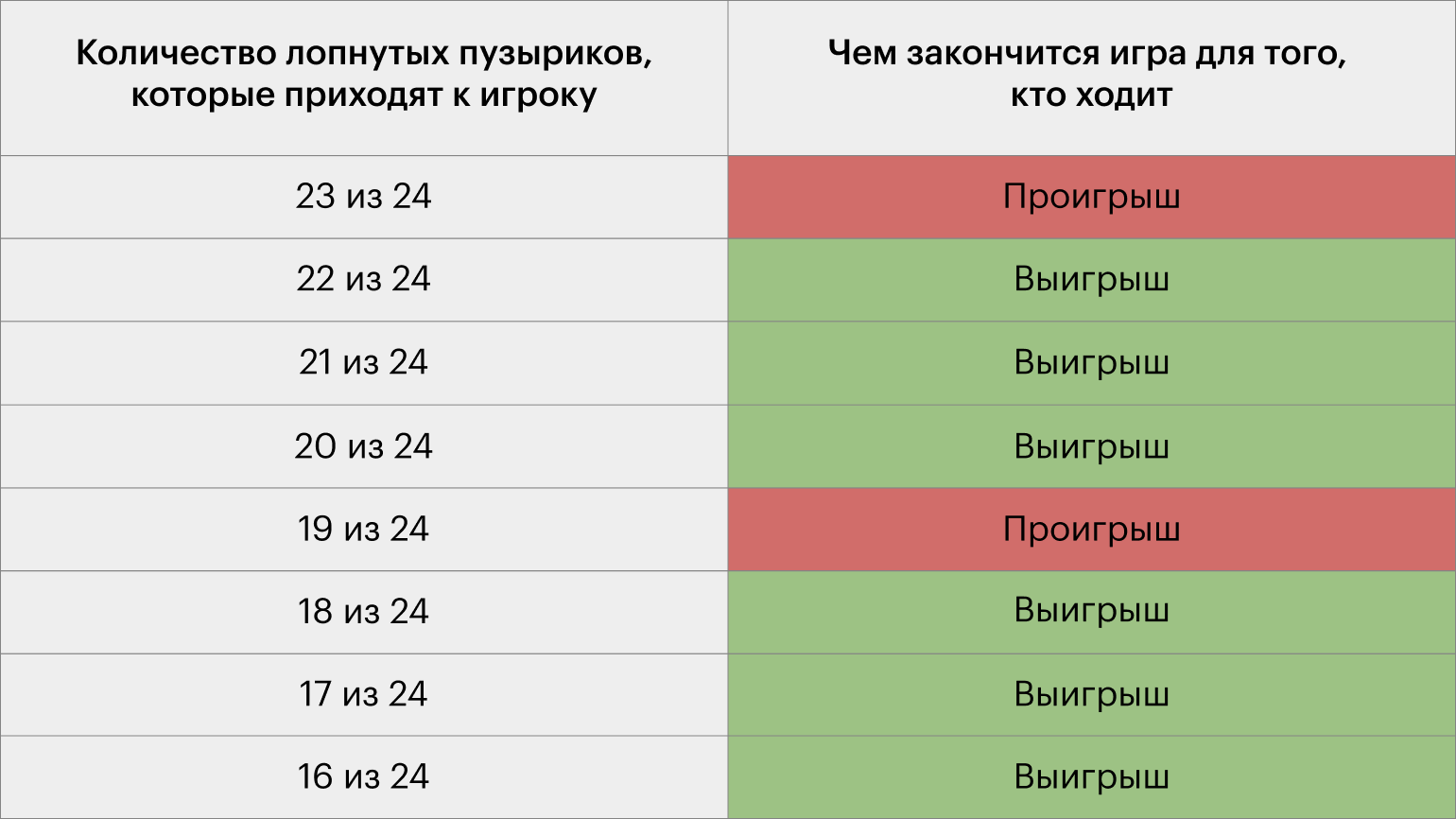
Лопаем 18 из 24 пузыриков. Соперник получает 6 свободных пузыриков и выиграет, если лопнет 1 пузырик — оставит в поп-ите 5 свободных пузыриков (лопнуты будут 19 из 24). То же произойдёт, если мы лопнем 17 из 24 или 16 из 24 пузыриков, — соперник лопнет 2 или 3 пузырика и мы опять получим поп-ит с 5 свободными пузыриками (лопнуты будут 19 из 24).
Шаг №4
Если мы проанализируем сделанные ходы, то обнаружим закономерность — каждая четвёртая позиция ведёт к проигрышу. Чтобы этим воспользоваться, нам нужно правильно сделать первый ход и удержать соперника в проигрышной позиции — добиться того, чтобы на последнем ходе он лопнул 1 пузырик и закончил игру.
В поп-ите 24 пузырика. Если мы разделим общее число пузыриков на 4, то в остатке получим 0 — не сможем загнать соперника в позицию, где он должен лопнуть последний пузырик. Поэтому для первого хода нам нужно подобрать число, ближайшее к 24 с остатком 1 при делении на 4. Этим числом будет 21. Получается, на первом ходе нам обязательно нужно лопнуть 3 пузырика (24 − 21 = 3).
После первого хода мы лопнули 3 пузырика и направили соперника в проигрышную позицию. Теперь, чтобы её удержать, необходимо после каждого хода соперника добивать сумму лопнутых пузыриков до 4. Вот все возможные варианты:
- он лопнул 2 пузырика — мы лопаем 2 пузырика;
- он лопает 1 пузырик — мы лопаем 3 пузырика;
- он лопает 3 пузырика — мы лопаем 1 пузырик.
Если мы будем постепенно уменьшать число пузыриков на 4, то до последнего хода в позициях соперника сохранится остаток 1 при делении на 4 — он не сможет победить и на последнем ходе будет вынужден лопнуть последний пузырик.
Ниже будет пример стратегии в действии. Поэкспериментируйте с ходами соперника — замените их на любые другие цифры и убедитесь, что это не влияет на результат.
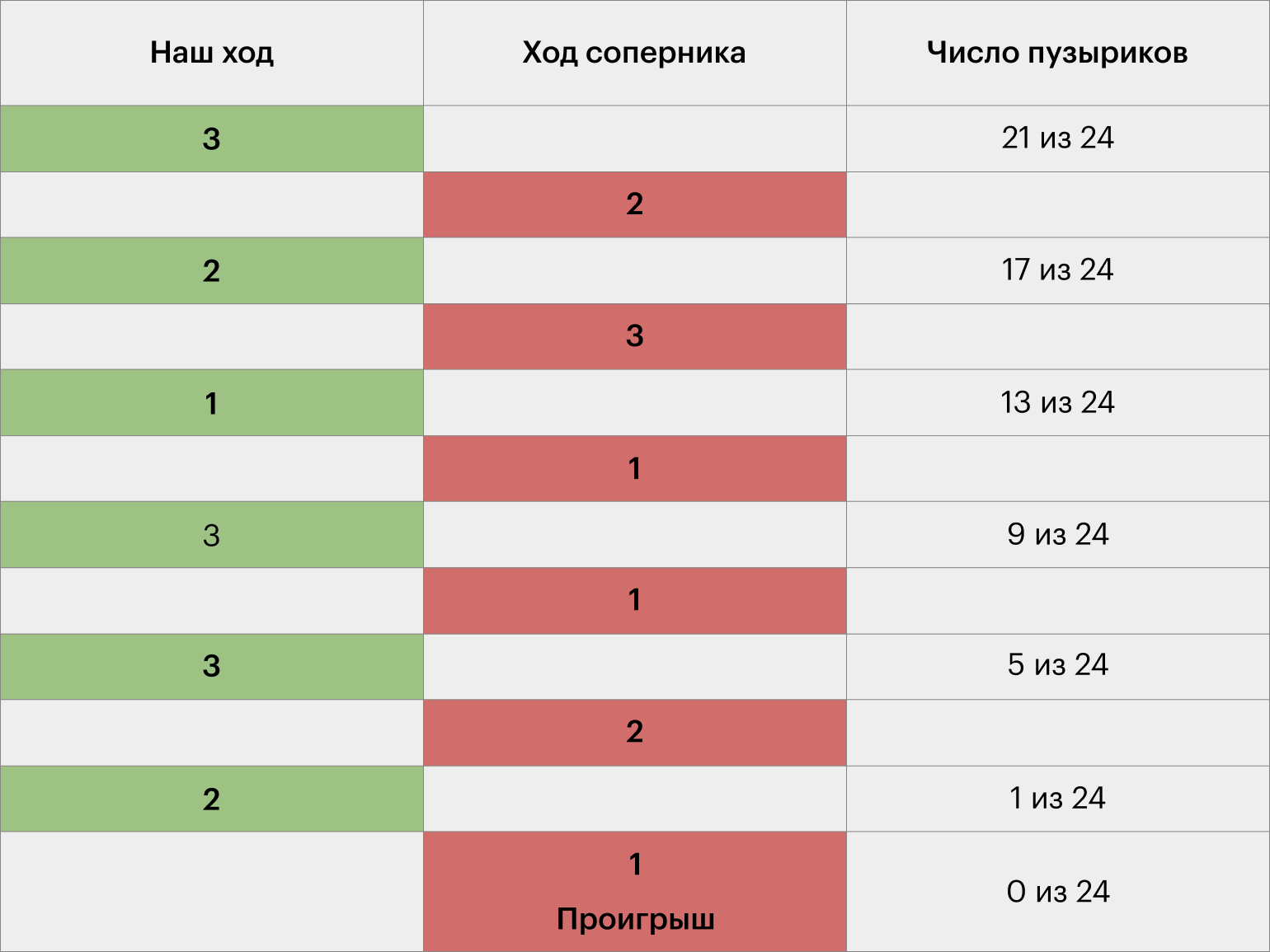
Ответы на задания со звёздочками
★ Если вы начинаете вторым номером, в поп-ите 24 пузырика и соперник знаком с выигрышной стратегией, то его не победить. Всё решает первый ход — кто его контролирует, тот и загоняет второго игрока в безвыходную проигрышную позицию.
★★ Если в поп-ите 21, 25, 29, 33 или больше пузыриков, то для первого игрока нет выигрышной стратегии. Мы не можем лопнуть 4 пузырика и отдать сопернику проигрышную позицию. Нам придётся лопать 1, 2 или 3 пузырика, и следующим ходом соперник на выбор лопнет 3, 2 или 1 пузырик и передаст нам ход — проигрышную позицию, которая даёт остаток 1 при делении на 4.