Библиотека NumPy: всё, что нужно знать новичку
Подробный гайд по самому популярному Python-инструменту для анализа данных и обучения нейронных сетей.
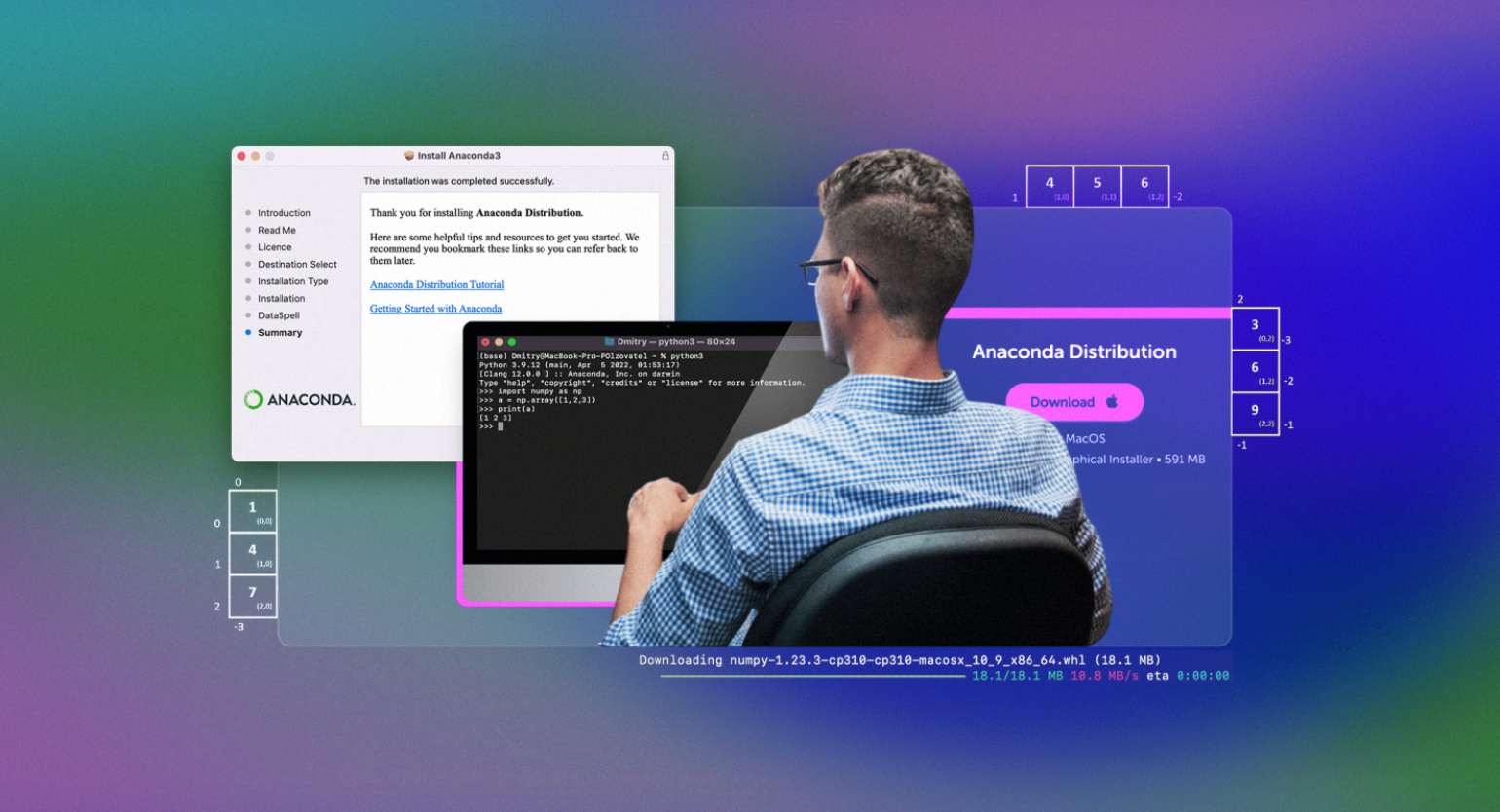

NumPy — это открытая бесплатная Python-библиотека для работы с многомерными массивами, этакий питонячий аналог Matlab. NumPy чаще всего используют в анализе данных и обучении нейронных сетей — в каждой из этих областей нужно проводить много вычислений с такими матрицами.
В этой статье мы собрали всё необходимое для старта работы с этой библиотекой — вам хватит получаса, чтобы разобраться в основных возможностях.
Содержание
Что такое NumPy и зачем она нужна
NumPy не просто работает с многомерными массивами, но и делает это быстро. Вообще, интерпретируемые языки производят вычисления медленнее компилируемых, а Python как раз язык интерпретируемый. NumPy же сделана так, чтобы эффективно работать с наборами чисел любого размера в Python.
Библиотека частично написана на Python, а частично на C и C++ — в тех местах, которые требуют скорости. Кроме того, код NumPy оптимизирован под большинство современных процессоров. Кстати, как и у Matlab, для NumPy существуют пакеты, расширяющие её функциональность, — например, библиотека SciPy или Matplotlib.
Инфографика: Оля Ежак для Skillbox Media
Массивы в NumPy отличаются от обычных списков и кортежей в Python тем, что они должны состоять только из элементов одного типа. Такое ограничение позволяет увеличить скорость вычислений в 50 раз, а также избежать ненужных ошибок с приведением и обработкой типов.
Как установить NumPy
Мы установим NumPy через платформу Anaconda, которая содержит много разных библиотек для Python. А ещё покажем, как это сделать через PIP.
NumPy можно также использовать через Jupyter Notebook, Google Colab или другими средствами — как вам удобнее. Поэтому выбирайте любой способ и пойдёмте изучать его.
Самый простой способ — Anaconda
Сначала надо зайти на официальный сайт Anaconda, чтобы скачать последнюю версию Python и NumPy: есть готовые пакеты под macOS, Windows и Linux.
Скриншот: Anaconda / Skillbox Media
Затем открываем установщик, соглашаемся со всеми пунктами и выбираем место для установки.
Скриншот: Anaconda / Skillbox Media
Чтобы убедиться, что Python точно установлен, открываем консоль и вводим туда команду python3 — должен запуститься интерпретатор Python, в котором можно писать код. Выглядит всё это примерно так:
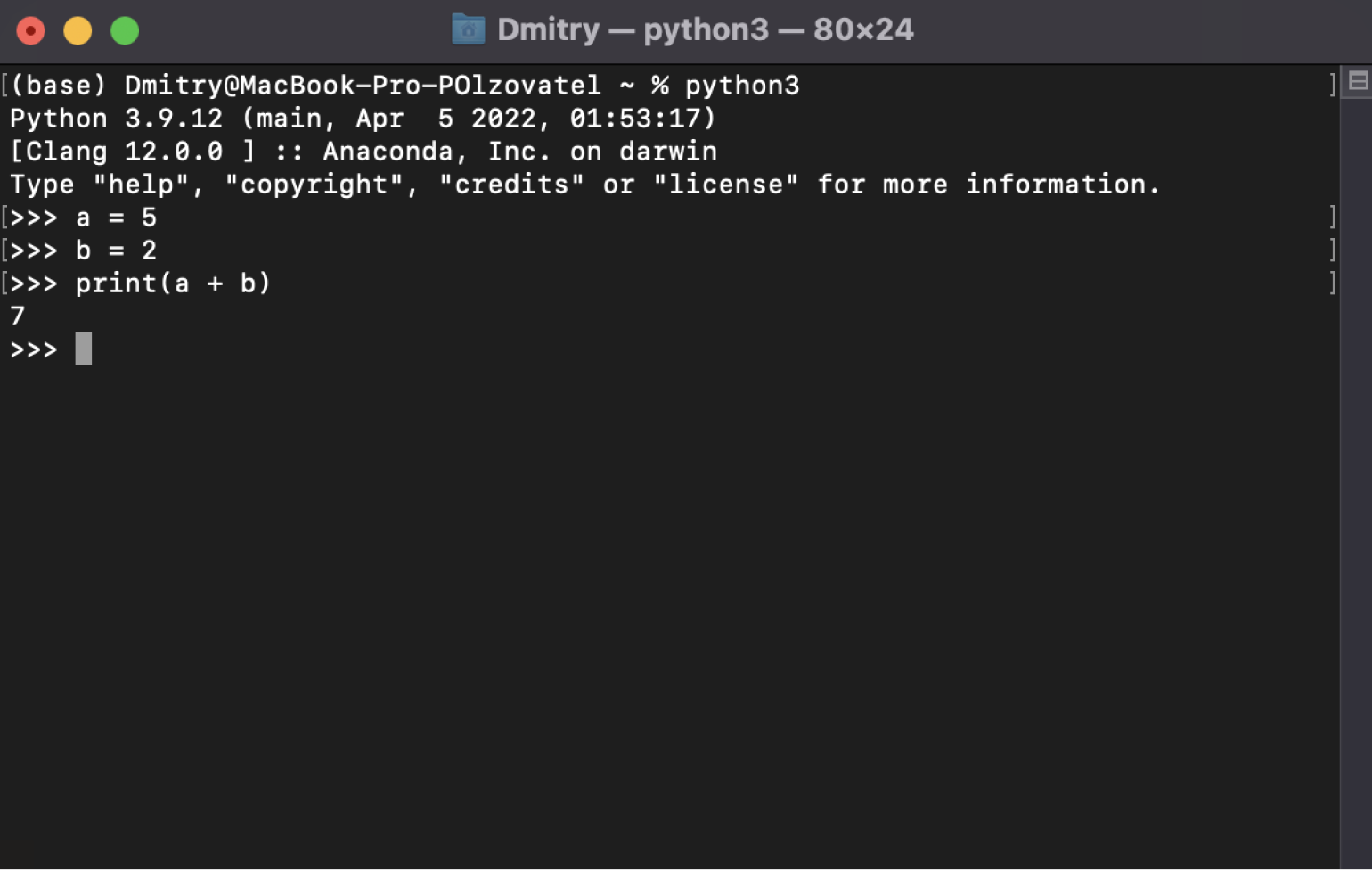
Скриншот: Skillbox Media
Anaconda уже содержит в себе много полезностей — например, NumPy, SciPy, Pandas. Поэтому больше ничего устанавливать не нужно. Достаточно проверить, что библиотека NumPy действительно работает. Введите в интерпретаторе Python в консоли такие команды — пока не важно, что это и как работает, об этом поговорим ниже.
import numpy as npСледом вот это:
a = np.array([1,2,3])А потом выводим значение переменной a — чтобы убедиться, что всё работает:
print(a)
Должно получиться что-то вроде вывода на скриншоте:
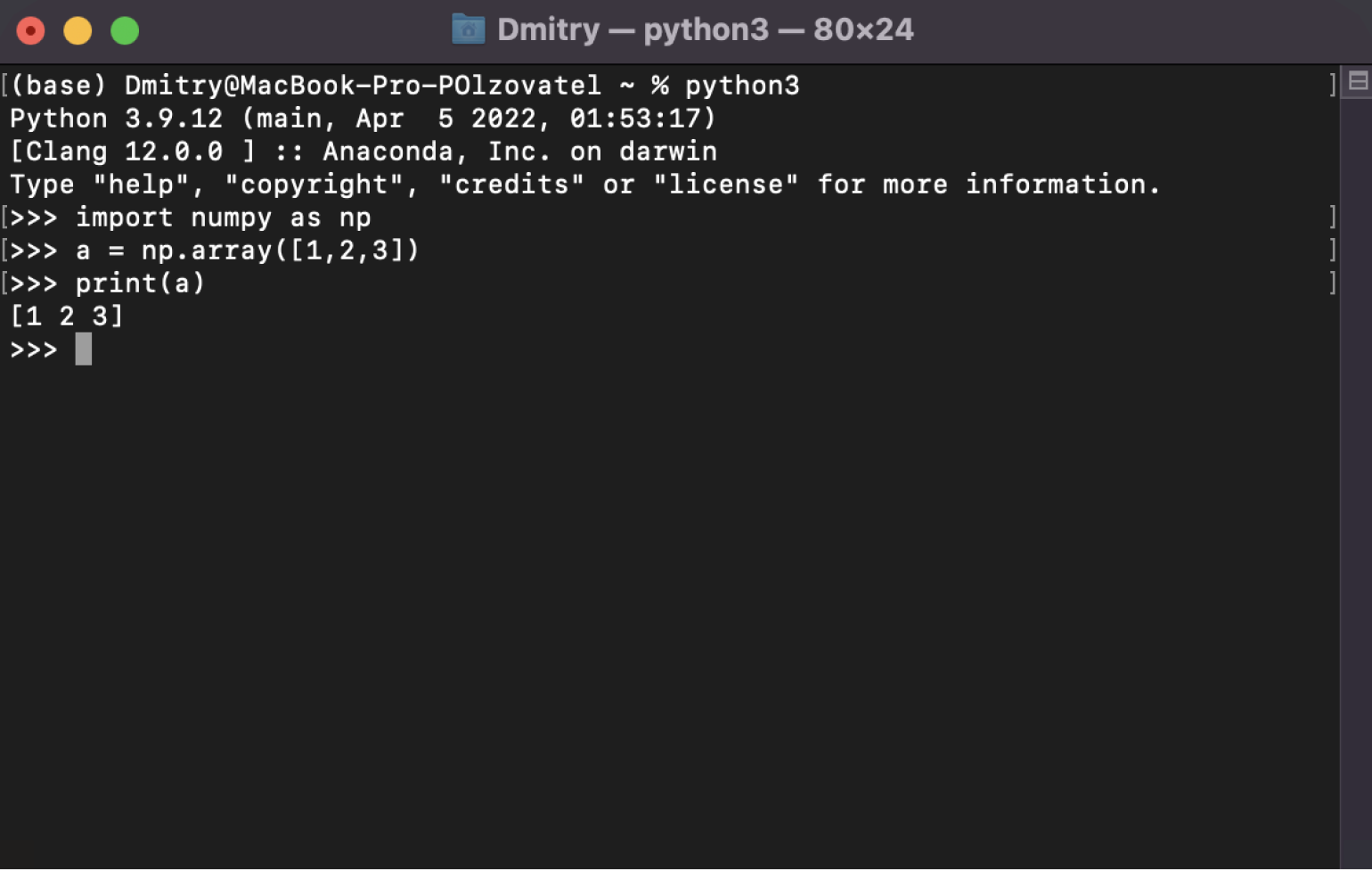
Скриншот: Skillbox Media
Без лишних файлов — через PIP
Если вам не хочется скачивать огромный пакет Anaconda, вы можете установить только NumPy с помощью встроенного питоновского менеджера пакетов PIP.
Для этого сначала нужно установить Python с официального сайта. Заходим на него, переходим во вкладку Downloads и видим справа последнюю актуальную версию Python:
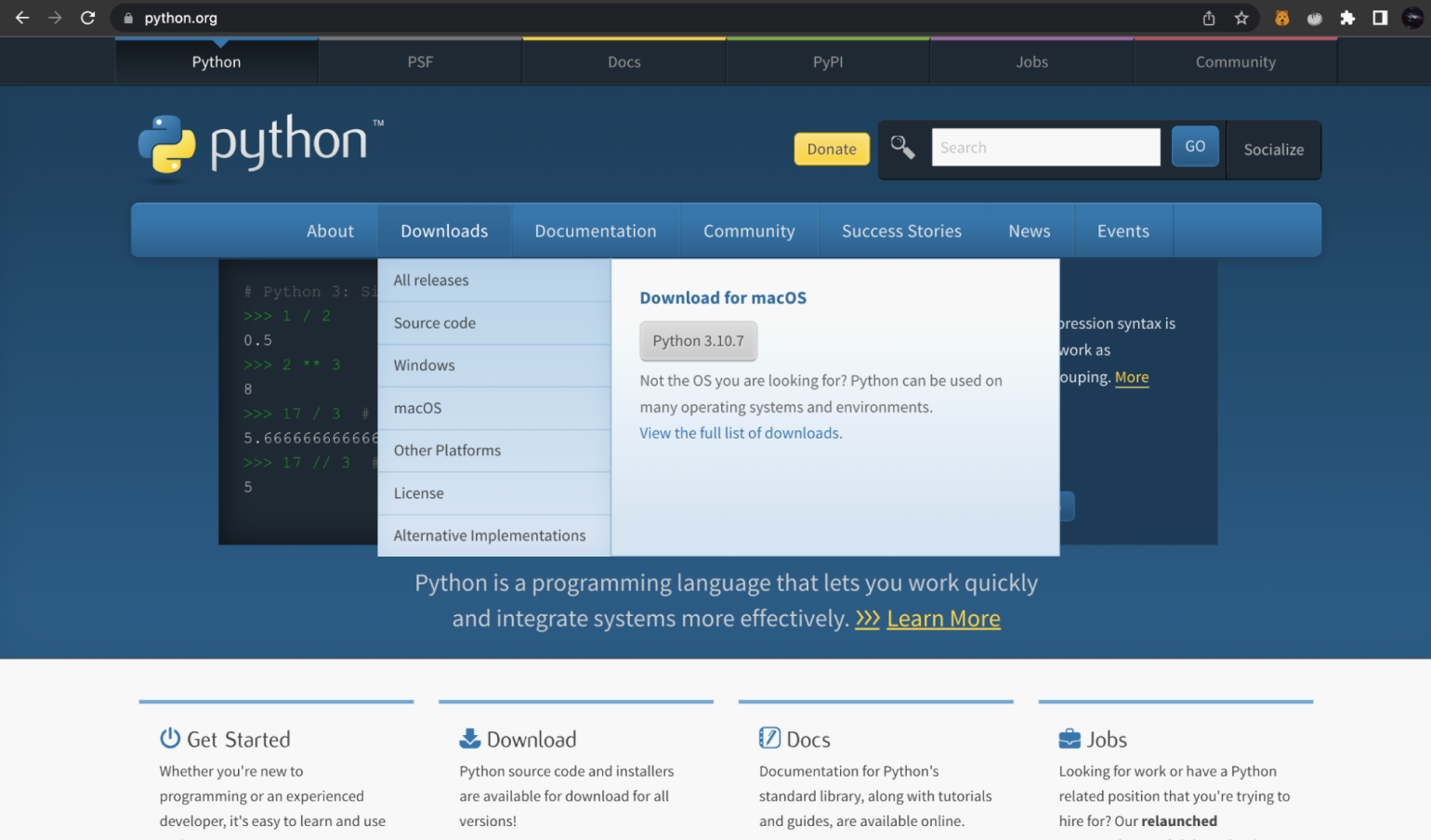
Скриншот: Skillbox Media
После этого начинается стандартная процедура: выбираем место установки и соглашаемся со всеми пунктами.
В конце нас должны поздравить.
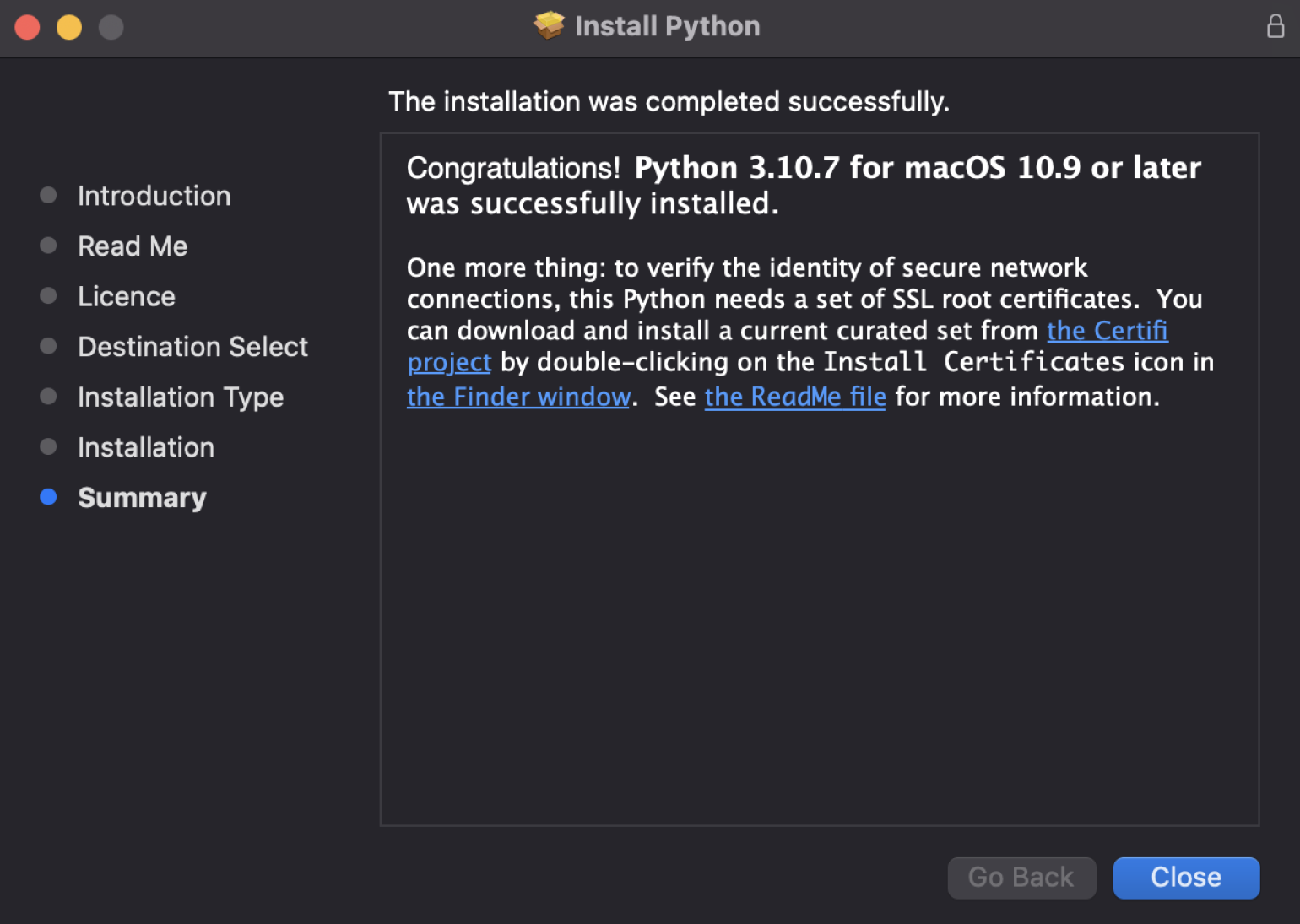
Скриншот: Skillbox Media
Теперь нужно скачать библиотеку NumPy. Открываем консоль и вводим туда команду:
pip install numpy
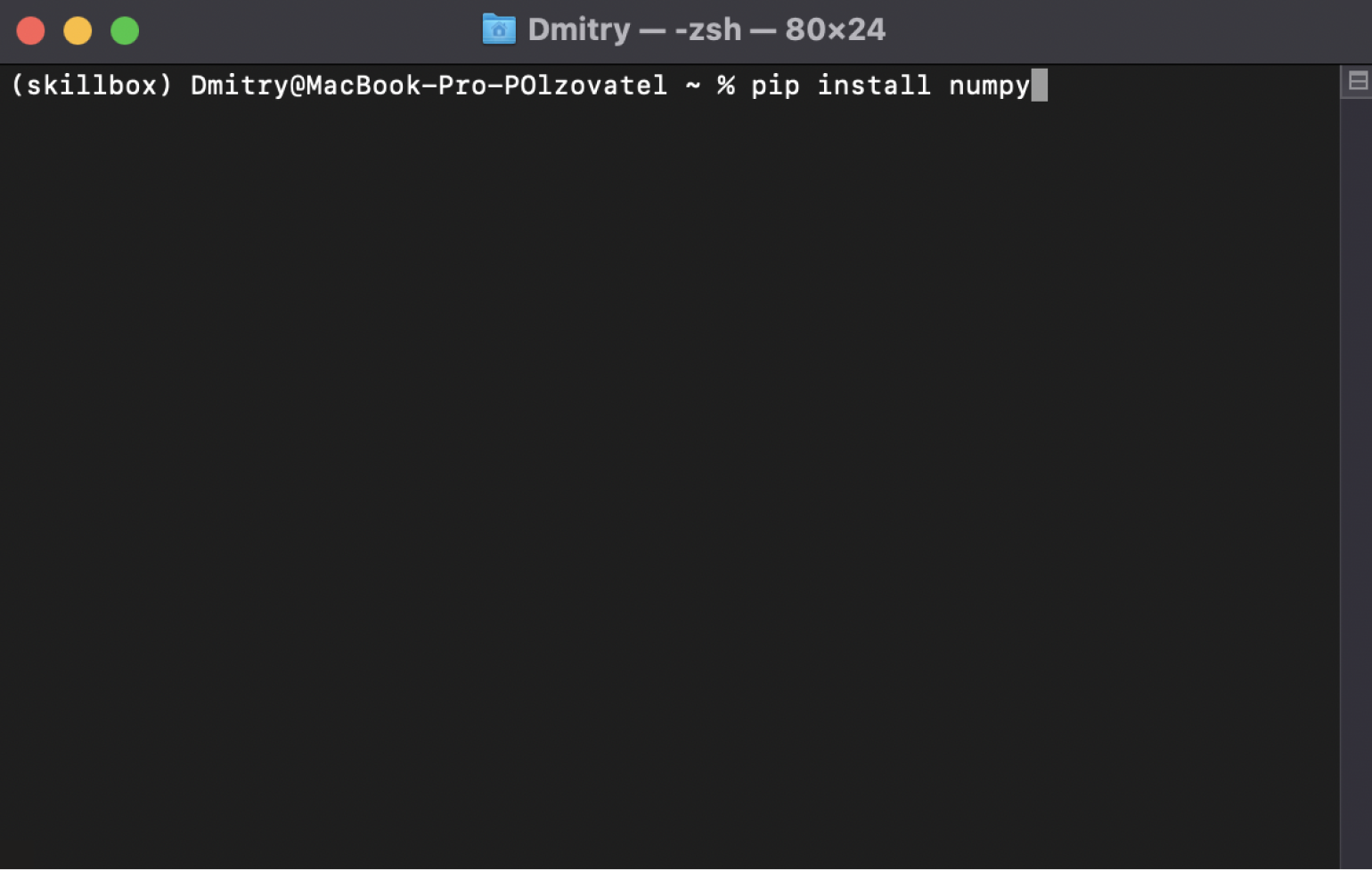
Скриншот: Skillbox Media
Если вдруг у вас выпала ошибка, значит, нужно написать другую похожую команду:
pip3 install numpy
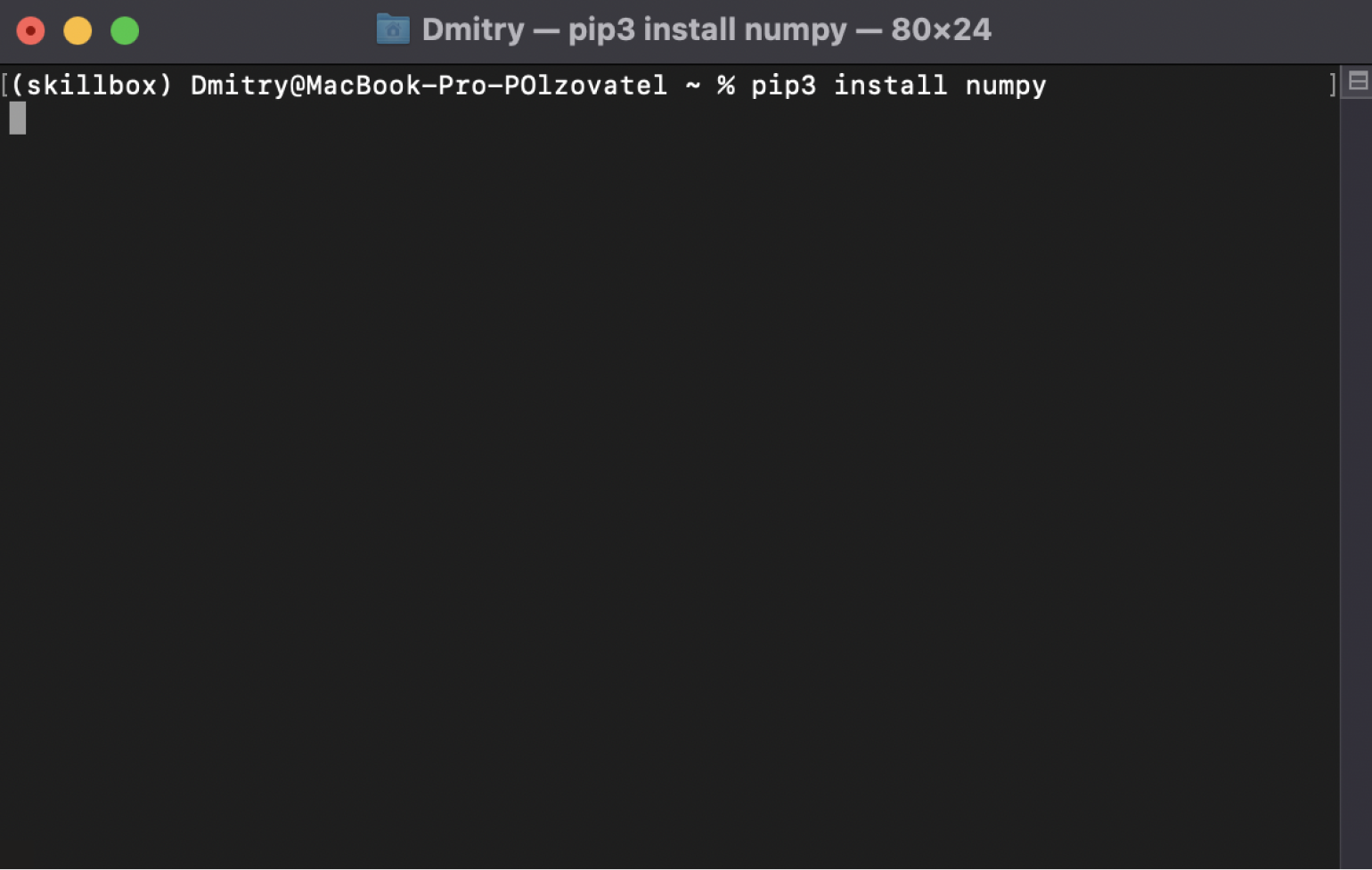
Скриншот: Skillbox Media
Теперь у нас точно должна установиться NumPy. Правда, тут нас уже никто не поздравляет — лишь сухо отмечают, что установка завершилась успешно.
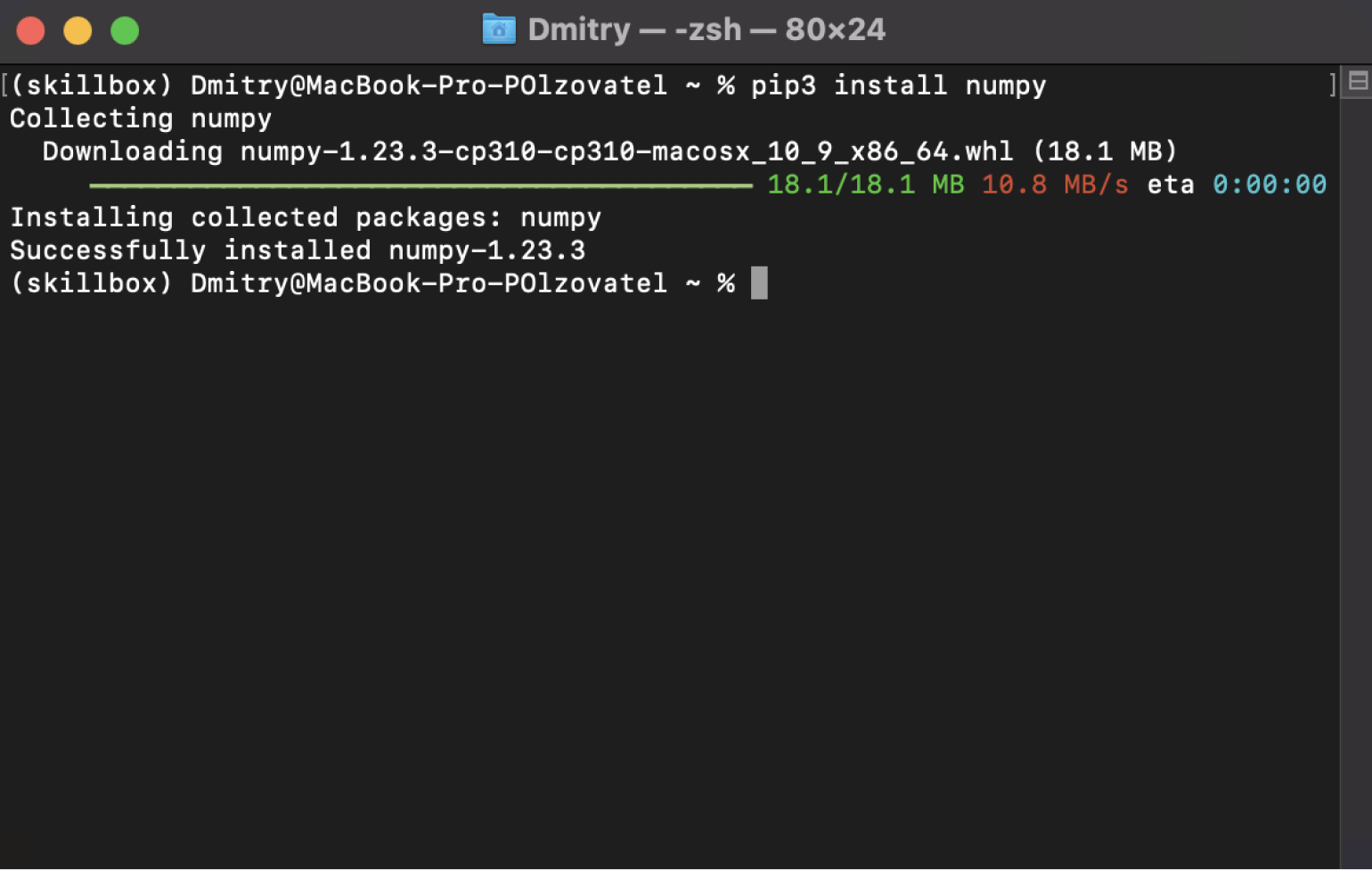
Скриншот: Skillbox Media
Подключаем NumPy
Перед тем как использовать NumPy, нужно подключить библиотеку в Python-коде — а вы думали, достаточно установить его? Нет, Python ещё должен узнать, что конкретно в этом проекте NumPy нам нужен.
import numpy as npnp — это уже привычное сокращение для NumPy в Python-сообществе. Оно позволяет быстро обращаться к методам библиотеки (две буквы проще, чем пять). Мы тоже будем придерживаться этого сокращения — мы же профессионалы! Хотя можно использовать NumPy и без присваивания отдельного сокращения или назвать её любыми приятными для вас буквами и символами. Но всё же рекомендуем следовать традициям сообщества, чтобы избежать недопонимания со стороны других программистов.
Основы NumPy
Теперь приступим к изучению базовых понятий и функций NumPy. А чтобы лучше усвоить изученный материал, рекомендуем внимательно изучать код, самостоятельно переписывать его и поиграться с параметрами и числами.
Как создавать массивы
Главный объект библиотеки NumPy — массив. Создаётся он очень просто:
a = np.array([1, 2, 3])Мы объявили переменную a и использовали встроенную функцию array. В неё нужно положить сам Python-список, который мы хотим создать. Он может быть любой формы: одномерный, двумерный, трёхмерный и так далее. Выше мы создали одномерный массив. Давайте создадим и другие:
a2 = np.array([[1, 2, 3], [4, 5, 6]])
a3 = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])Получилось огромное количество скобок. Чтобы понять, как всё это выглядит, воспользуемся функцией print:
print(a)
# [1 2 3]
print(a2)
# [[1 2 3]
# [4 5 6]]
print(a3)
# [[[1 2 3]
# [4 5 6]]
# [[7 8 9]
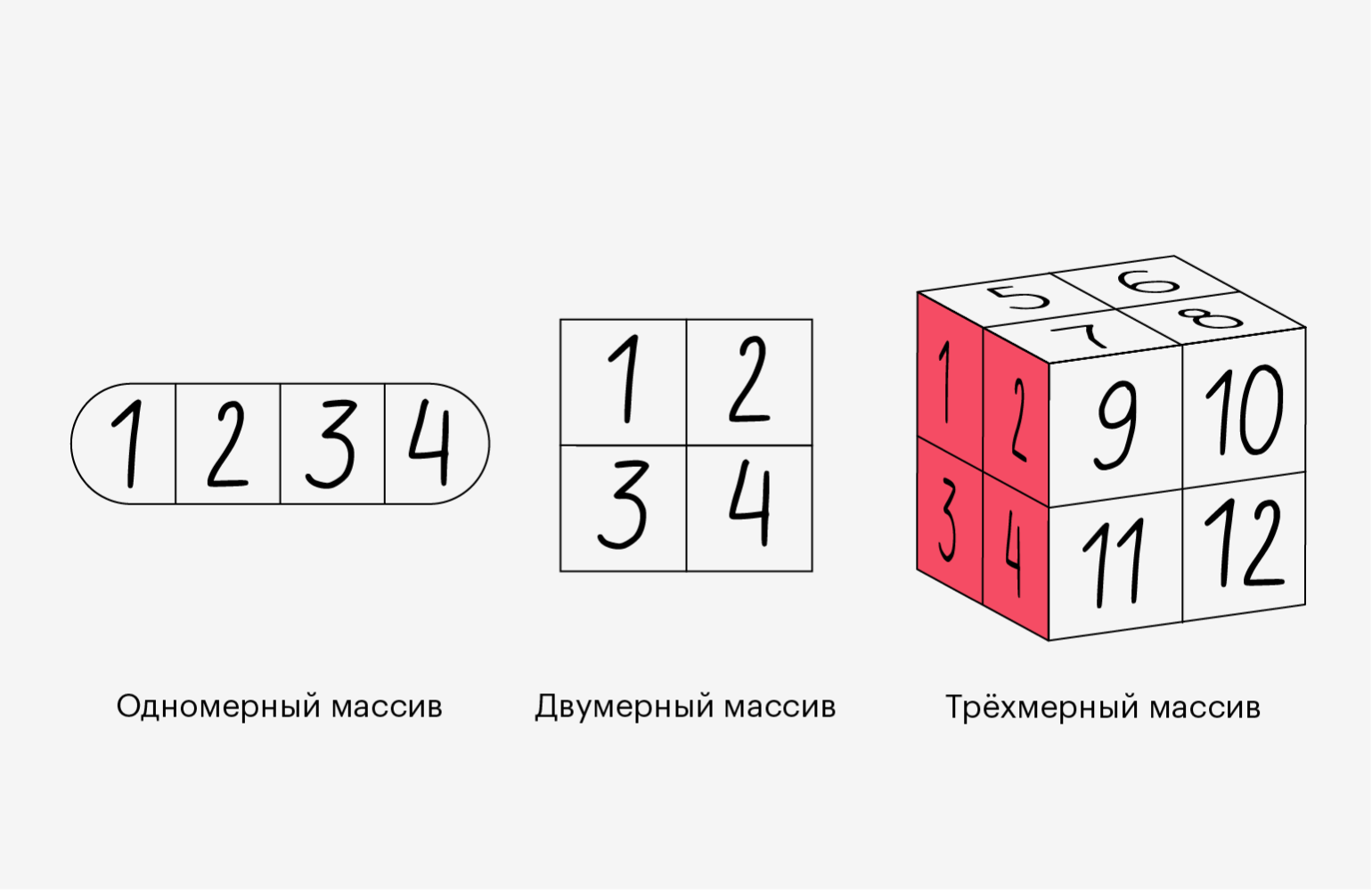
# [10 11 12]]]Как мы видим, в первом случае получился двумерный массив, который состоит из двух одномерных. А во втором — трёхмерный, состоящий из двумерных. Если двигаться вверх по измерениям, то они будут следовать похожей логике:
- четырёхмерный состоит из трёхмерных;
- пятимерный — это несколько четырёхмерных;
- n-мерный — это несколько (n-1)-мерных.
Проще показать это на иллюстрации (главное, не потеряйтесь в измерениях):
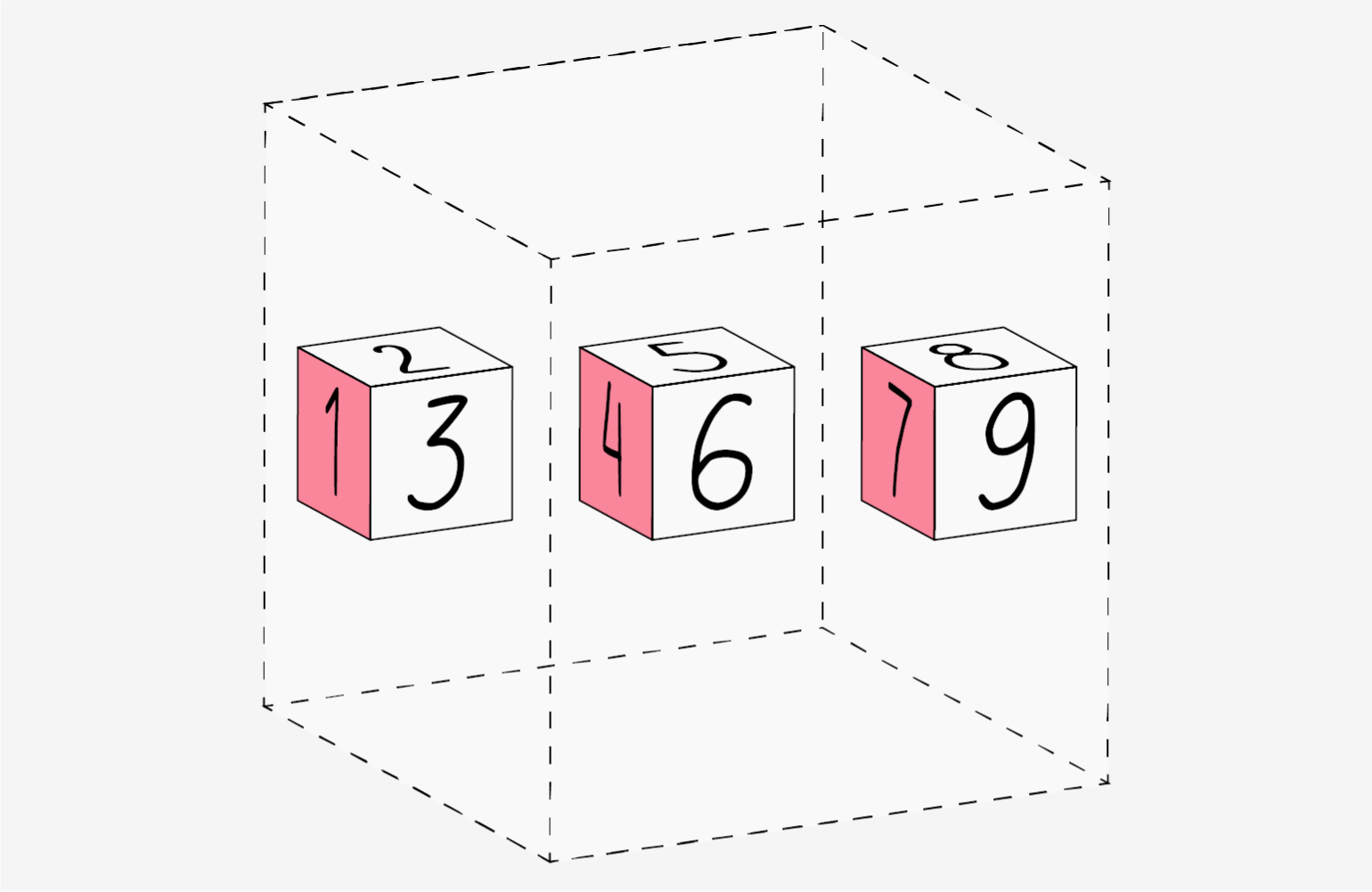
Инфографика: Оля Ежак для Skillbox Media
В NumPy-массивы можно передавать не только целые числа, но и дробные:
b = np.array([1.4, 2.5, 3.7])
print(b)
# [1.4 2.5 3.7]А если вы хотите указать конкретный тип, то это можно сделать с помощью дополнительного параметра dtype:
c = np.array([1, 2, 3], dtype='float32')
print(c)
# [1. 2. 3.]Целые числа сразу были приведены к числам с плавающей точкой. Таких преобразований существует много — они нужны, чтобы не занимать лишнюю память. Например, числа int32 занимают 32 бита, или 4 байта, а int16 — 16 бит, или 2 байта. Программисты используют параметр dtype, когда точно знают, что их переменные будут находиться в диапазоне от −32 768 до 32 767.
Если реальные значения элементов массива выйдут за рамки явно указанного типа, то их значения в какой-то момент просто обнулятся и начнут отсчёт заново:
# Для примера определим переменную типа int16
a = np.int16(32000)
b = np.int16(768)
# Выполним сложение с переполнением
result = np.int16(a + b)
# Проверим результат, который сбросится до своего минимального значения -32768
print(result)
# Out: -32768Базовые функции
Теперь, когда мы умеем создавать массивы и задавать им разные значения, давайте узнаем, какие у них есть встроенные функции.
Допустим, у нас есть такой объект:
a = np.array([1,2,3], dtype='int32')
print(a)
# [1 2 3]Чтобы узнать, сколько у него измерений, воспользуемся функцией ndim:
print(a.ndim)
# 1Всё верно, ведь у нас одномерный массив, или вектор. Если бы он был двумерным, то и результат оказался бы другим:
b = np.array([[1, 2, 3], [4, 5, 6]])
print(b.ndim)
# 2Хорошо, с размерностью понятно. А как посчитать количество строк и столбцов? Для этого есть функция shape:
print(a.shape)
# (3,)Получилось слегка странно, но всему есть объяснение. Дело в том, что вектор — это всего лишь одномерный массив. У векторов в библиотеке NumPy есть только строки — или элементы. Поэтому функция shape выдала число 3.
С двумерными наборами данных ситуация понятнее:
print(b.shape)
# (2, 3)В b две строки и три столбца.
Для трёхмерных и n-мерных массивов функция shape будет добавлять дополнительные числа в кортеже через запятую:
с = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print(с.shape)
# (2, 2, 3)Читается это так: в объекте c два трёхмерных массива с двумя строками и тремя столбцами.
Кроме размерностей, можно также узнать тип элементов — в этом поможет функция dtype (не путайте её с одноимённым параметром):
a = np.array([1,2,3], dtype='int32')
print(a.dtype)
# Out: int32Если не присваивать тип элементам вручную, по умолчанию будет задан int32.
Ещё можно узнать количество элементов с помощью функции size:
print(a.size)
# 3А через функции itemsize и nbytes можно узнать, какое количество байт в памяти занимает один элемент и какое количество байт занимает весь массив:
b = np.array([[1, 2, 3], [4, 5, 6]], dtype='int16')
print(b.itemsize)
# 2
print(b.nbytes)
# 12Один элемент занимает 2 байта, а весь объект b из 6 элементов — 2 × 6 = 12 байтов.
Доступ к элементам
В NumPy можно обращаться к отдельным элементам, строкам или столбцам, а также точечно выбирать последовательность нужных элементов. Рассмотрим всё подробнее.
Допустим, у нас есть двумерный массив:
a = np.array([[1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14]])
print(a)
# Out:
# [[ 1 2 3 4 5 6 7]
# [ 8 9 10 11 12 13 14]]И мы хотим достать из него элемент, который находится в первой строке на пятом месте. Сделать это можно с помощью специального оператора []:
print(a[0, 4])
# 5Почему 0 и 4? Потому что нумерация элементов в Python начинается с нуля, а значит, первая строка будет нулевой, а пятый столбец — четвёртым.
Если бы у нас был трёхмерный массив, обращение к его элементам было бы похожим:
c = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print(c)
# Out:
# [[[ 1 2 3]
# [ 4 5 6]]
# [[ 7 8 9]
# [10 11 12]]]
print(c[1, 1, 1])
# 11Здесь мы сначала обратились ко второму двумерному массиву, а затем выбрали в нём вторую строку и второй столбец. Там и находилось число 11.
Кроме отдельных элементов, в библиотеке NumPy можно обратиться к целой строке или столбцу с помощью оператора :. Он позволяет выбрать все элементы указанной строки или столбца:
a = np.array([[1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14]])
print(a[0, :])
# [1 2 3 4 5 6 7]
print(a[:, 0])
# [1 8]В первом случае мы выбрали всю первую строку, а во втором — первый столбец.
Ещё можно использовать продвинутые способы выделения нужных нам элементов.
Кстати, оператор : на самом деле представляет собой сокращённую форму конструкции начальный_индекс:конечный_индекс:шаг.
Давайте остановимся на ней подробнее:
b = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(b[0, 1:4:2])
# [2 4]Мы указали, что хотим выбрать первую строку, а затем уточнили, какие именно столбцы нам нужны: 1:4:2.
- Первое число означает, что мы начинаем брать элементы с первого индекса — второго столбца. В примере это число 2.
- Второе число — что мы заканчиваем итерацию на четвёртом индексе, то есть проходим всю строку.
- Третье число указывает, с каким шагом мы идём по строке. В нашем примере — с шагом в два элемента. То есть мы пройдём по элементам 1 и 3, которые соответствуют числам 2 и 4.
Давайте посмотрим на другой пример:
a = np.array([[1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14]])
print(a)
# Out:
# [[ 1 2 3 4 5 6 7]
# [ 8 9 10 11 12 13 14]]
print(a[1, 0:-1:3])
# [ 8 11]Здесь мы использовали отрицательные индексы — они позволяют считать индексы элементов справа налево. –1 означает, что последний индекс — это последний столбец второй строки. Заметьте, что 6-й столбец не вывелся. Это значит, что NumPy не доходит до этого индекса, а заканчивает обход на один индекс раньше.

Инфографика: Оля Ежак для Skillbox Media
Ещё мы можем менять значения в NumPy-массиве с помощью той же операции доступа к элементам. Например:
c = np.array([[0, 2], [4, 6]])
c[0, 0] = 1
print(c)
# [[1 2]
# [4 6]]Мы заменили элемент из первой строки и первого столбца (элемент 0) на единицу. И наш список данных успешно изменился.
Кроме отдельных элементов, можно заменять любые последовательности элементов с помощью конструкции начальный_индекс:конечный_индекс:шаг и её упрощённой версии — :.
c = np.array([[0, 2], [4, 6]])
c[0, :] = [3, 3]
print(c)
# [[3 3]
# [4 6]]Теперь в переменной с вся первая строка заменилась на тройки. Главное при такой замене — учитывать размер строки, чтобы не возникло ошибок. Например, если присвоить первой строке вектор из трёх элементов, интерпретатор будет ругаться:
c = np.array([[0, 2], [4, 6]])
c[0, :] = [3, 3, 3]
print(c)
# Out:
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# c[0, :] = [3, 3, 3]
# ~^^^^^^
# ValueError: could not broadcast input array from shape (3,) into shape (2,)Текст ошибки сообщает, что нельзя присвоить одномерному массиву с размером 2 массив размером 3.
Создание специальных массивов
Мы научились создавать массивы любой размерности. Но иногда хочется создать их с уже заполненными значениями — например, забить все ячейки нулями или единицами. NumPy может и это.
Массив из нулей. Чтобы создать его, используем функцию zeros.
a = np.zeros((2, 2))
print(a)
# [[0. 0.]
# [0. 0.]]Первое, что нужно помнить, — как задавать размер. Он задаётся кортежем (2, 2). Если указать размер без скобок, то снова получим ошибку:
a = np.zeros(2, 2)
print(a)
# Out:
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# a = np.zeros(2, 2)
# ^^^^^^^^^^^^^^
# TypeError: Cannot interpret '2' as a data typeА всё потому, что без скобок NumPy расценивает второй элемент (число 2) как тип данных, который должен быть указан для параметра dtype.
Если указать только одно число, создастся вектор размером два элемента. В этом случае уже не нужно ставить дополнительные скобки:
a = np.zeros(2)
print(a)
# [0. 0.]Ещё стоит отметить, что элементам по умолчанию присваивается тип float64. Это дробные числа, которые занимают в памяти 64 бита, или 8 байт. Если нужны именно целые числа, то мы по старой схеме указываем это в параметре dtype — через запятую:
a = np.zeros(2, dtype='int32')
print(a)
# [0 0]Массив из единиц. Он создаётся точно так же, как и из нулей, но используется функция ones:
b = np.ones((4, 2, 2), dtype='int32')
print(b)
# Out:
# [[[1 1]
# [1 1]]
# [[1 1]
# [1 1]]
# [[1 1]
# [1 1]]
# [[1 1]
# [1 1]]]Здесь мы создали трёхмерный массив из четырёх двумерных, каждый из которых имеет две строки и два столбца. А также указали, что элементы должны иметь тип int32.
Массив из произвольных чисел. Иногда бывает нужно заполнить массив какими-то отличными от нуля и единицы числами. В этом поможет функция full:
c = np.full((2, 2), 5)
print(c)
# [[5 5]
# [5 5]]Здесь мы сначала указали, какой размер должен быть у массива через кортеж, — (2,2), а затем число, которым мы хотим заполнить все его элементы, — 5.
Равно как и у функций zeros и ones, элементы по умолчанию будут иметь тип float64. А размер должен передаваться в виде кортежа — (2, 2).
Массив случайных чисел. Он создаётся с помощью функции random.rand:
d = np.random.rand(3, 2)
print(d)
# Out:
# [[0.22815968 0.61195664]
# [0.85115576 0.36586858]
# [0.32893068 0.6239481]]Получилось что-то странное. Но так и должно быть — ведь NumPy генерирует случайные числа в диапазоне от 0 до 1 с восемью знаками после запятой.
Ещё одна странность — то, как задаётся размер. Здесь это нужно делать не через кортеж (3, 2), а просто указывая размерности через запятую. Всё потому, что в функции random.rand нет параметра dtype.
Чтобы создать массив случайных чисел, нужно воспользоваться функцией random.randint:
e = np.random.randint(-5, 10, size=(4, 4))
print(e)
# Out:
# [[ 4 2 2 1]
# [ 0 4 -1 -4]
# [-3 -4 3 9]
# [-3 5 5 -5]]У нас получился массив размером четыре на четыре — size=(4, 4) — с целыми числами из диапазона от –5 до 10. Как и в предыдущем случае, создаётся такой массив слегка странно — но такова жизнь NumPy-программистов.
Единичная матрица. Она нужна тем, кто занимается линейной алгеброй. По диагонали такой матрицы элементы равны единице, а все остальные элементы — нулю. Создаётся она с помощью функции identity или eye:
i = np.identity(4)
print(i)
# Out:
# [[1. 0. 0. 0.]
# [0. 1. 0. 0.]
# [0. 0. 1. 0.]
# [0. 0. 0. 1.]]Здесь задаётся только количество строк матрицы, потому что единичная матрица должна быть симметричной — иметь одинаковое количество строк и столбцов.
И всё также можно указать тип элементов с помощью параметра dtype:
i = np.identity(4, dtype='int32')
print(i)
# Out:
# [[1 0 0 0]
# [0 1 0 0]
# [0 0 1 0]
# [0 0 0 1]]Математические операции
Массивы из NumPy поддерживают все стандартные арифметические операции — например, сложение, деление, вычитание. Работает это поэлементно:
a = np.array([1, 2, 3, 4])
print(a)
# [1 2 3 4]
print(a + 3)
# [4 5 6 7]К каждому элементу a прибавилось число 3, а размерность не изменилась. Все остальные операции работают точно так же:
a = np.array([1, 2, 3, 4])
print(a - 2)
# [-1 0 1 2]
print(a * 2)
# [2 4 6 8]
print(a / 2)
# [0.5 1. 1.5 2. ] # Здесь тип элементов приведён к 'float64'
print(a ** 2)
# [ 1 4 9 16]Ещё можно проводить любые математические операции с массивами одинакового размера:
a = np.array([[1, 2], [3, 4]])
b = np.array([[2, 2], [2, 2]])
print(a + b)
# [[3 4]
# [5 6]]
print(a * b)
# [[2 4]
# [6 8]]
print(a ** b)
# [[ 1 4]
# [ 9 16]]Здесь каждый элемент a складывается, умножается и возводится в степень на элемент из такой же позиции массива b.
Кроме примитивных операций, в NumPy можно проводить и более сложные — например, вычислить косинус:
a = np.array([[1, 2], [3, 4]])
print(np.cos(a))
# [[ 0.54030231 -0.41614684]
# [-0.9899925 -0.65364362]]Все математические функции вызываются по похожему шаблону: сначала пишем np.название_математической_функции, а потом передаём внутрь массив — как мы и сделали выше.
Ещё можно применять различные операции из линейной алгебры, математической статистики и так далее. Давайте для примера перемножим матрицы по правилам линейной алгебры:
a = np.ones((2, 3))
print(a)
# [[1. 1. 1.]
# [1. 1. 1.]]
b = np.full((3, 2), 2)
print(b)
# [[2 2]
# [2 2]
# [2 2]]
print(np.matmul(a, b))
# [[6. 6.]
# [6. 6.]]Не будем разбирать математическую составляющую — предполагается, что вы уже знакомы с математикой и используете NumPy для выражения операций языком программирования. Полный список всех поддерживаемых в библиотеке операций можно найти в официальной документации.
Статистические операции
Если нужно вычислить среднее значение массива, его медиану, дисперсию или другие статистические показатели, то нам помогут агрегатные функции. В NumPy агрегатные функции — это методы, которые применяются к массиву и возвращают одно итоговое значение. Общая формула: агрегатор.массив().
У агрегатных функций есть необязательный параметр axis. Он указывает на ось, вдоль которой будет производиться вычисление. Напоминаем, что у массива может быть одна или несколько осей в зависимости от размерности:
- Ось (axis) 0. Это первая ось, которая соответствует направлению вниз по строкам. Если у нас двумерный набор данных и мы просуммируем элементы вдоль оси 0, то получим сумму элементов каждого столбца.
- Ось (axis) 1. Это вторая ось, которая проходит вдоль второго измерения массива. В двумерной структуре она соответствует направлению по столбцам. Если мы просуммируем элементы вдоль оси 1, то в результате получим сумму элементов каждой строки.
- Ось (axis) 2 и далее. Это дополнительные оси для массивов с тремя и более измерениями. Ось 2 — третья ось, ось 3 — четвёртая и так далее. Каждая последующая ось будет добавлять новое измерение и направление для массивов большей размерности.
Если мы используем агрегатную функцию sum без параметров, то она вернёт сумму всех элементов. А если указать sum (axis=0), то будет возвращена сумма элементов вдоль первой оси. Параметр axis не должен превышать количество осей массива. То есть для одномерного массива он не может превышать 0, для двумерного — 1 и так далее. Вот как это работает:
# Создаём двумерный массив
a = np.array([[1, 2, 3], [4, 5, 6]])
# Вычисляем сумму всех элементов массива
total_sum = a.sum()
print(total_sum)
# 21
# Вычисляем сумму элементов вдоль оси 0 (суммируем столбцы)
sum_along_axis0 = a.sum(axis=0)
print(sum_along_axis0)
# [5 7 9]
# Вычисляем сумму элементов вдоль оси 1 (суммируем строки)
sum_along_axis1 = a.sum(axis=1)
print(sum_along_axis1)
# [ 6 15]Мы рассмотрели пример с агрегатной функцией sum, которая рассчитывает сумму всех элементов массива или оси. Теперь разберём другие агрегаторы.
С помощью функции mean можно вычислить среднее арифметическое значение — сумму выбранных элементов, делённую на их количество:
a = np.array([[1, 2, 3], [4, 5, 6]])
# Среднее арифметическое всех элементов массива
mean_all = a.mean()
print(mean_all)
# 3.5
# Среднее арифметическое элементов вдоль оси 0
mean_axis0 = a.mean(axis=0)
print(mean_axis0)
# [2.5 3.5 4.5]
# Среднее арифметическое элементов вдоль оси 1
mean_axis1 = a.mean(axis=1)
print(mean_axis1)
# [2. 5.]Агрегаторы min и max находят минимальное и максимальное значение:
a = np.array([[1, 2, 3], [4, 5, 6]])
# Минимальное значение среди всех элементов массива
min_all = a.min()
print(min_all)
# 1
# Минимальное значение среди элементов вдоль оси 0
min_axis0 = a.min(axis=0)
print(min_axis0)
# [1 2 3]
# Минимум значение среди элементов вдоль оси 1
min_axis1 = a.min(axis=1)
print(min_axis1)
# [1 4]Если воспользуемся функцией prod, то вычислим произведение элементов:
a = np.array([[1, 2, 3], [4, 5, 6]])
# Произведение всех элементов массива
prod_all = a.prod()
print(prod_all)
# 720
# Произведение элементов вдоль оси 0
prod_axis0 = a.prod(axis=0)
print(prod_axis0)
# [ 4 10 18]
# Произведение элементов вдоль оси 1
prod_axis1 = a.prod(axis=1)
print(prod_axis1)
# [ 6 120]Ещё посмотрим работу функции var, которая определяет дисперсию, — узнаем, насколько данные отличаются друг от друга и от среднего значения:
a = np.array([[1, 2, 3], [4, 5, 6]])
# Дисперсия всех элементов массива
var_all = a.var()
print(var_all)
# 2.9166666666666665
# Дисперсия элементов вдоль оси 0
var_axis0 = a.var(axis=0)
print(var_axis0)
# [2.25 2.25 2.25]
# Дисперсия элементов вдоль оси 1
var_axis1 = a.var(axis=1)
print(var_axis1)
# [0.66666667 0.66666667]О других агрегаторах читайте в документации в разделе «Статистика».
Копирование и организация
Если в NumPy вы присвоите массив другой переменной, то просто создадите ссылку на него. Разберём на примере:
a = np.array([1, 2, 3])
b = a
b[0] = 5
print(b)
# [5 2 3]
print(a)
# [5 2 3]Как мы видим, при изменении b меняется также и a. Дело в том, что массивы в NumPy — это только ссылки на области в памяти. Поэтому, когда мы присвоили a переменной b, на самом деле мы просто присвоили ей ссылку на первый элемент a в памяти.
Чтобы создать независимую копию a, используйте функцию copy:
a = np.array([1, 2, 3])
b = a.copy()
b[0] = 5
print(b)
# [5 2 3]
print(a)
# [1 2 3]Для организации массива мы можем менять его форму (shape) и размер (size). Форма — это структура, которая представлена в виде кортежей и определяет количество элементов вдоль каждой оси. Размер — это общее количество элементов. Например, форма (2, 3) означает, что массив имеет две строки и три столбца. А вот размер 6 указывает на то, что внутри массива находится шесть элементов.
Ещё мы можем менять размер массива с помощью функции reshape:
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(a)
# Out:
# [[1 2 3 4]
# [5 6 7 8]]
b = a.reshape((4, 2))
print(b)
# Out:
# [[1 2]
# [3 4]
# [5 6]
# [7 8]]Изначально размер a был 2 на 4. Мы переделали его под 4 на 2. Заметьте: новые размеры должны соответствовать количеству элементов. В противном случае Python вернет ошибку:
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
b = a.reshape((4, 3))
print(b)
# Out:
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# b = a.reshape((4, 3))
# ^^^^^^^^^^^^^^^^^
# ValueError: cannot reshape array of size 8 into shape (4,3)Ещё мы можем воспользоваться функцией resize, которая изменяет форму и размер. Если новый размер больше исходного, то элементы повторяться или заполняться нулями. Если, наоборот, новый размер будет меньше исходного, то лишние элементы функция отбросит:
a = np.array([1, 2, 3])
b = np.resize(a, (2, 4))
# Исходный массив
print(a)
# [1 2 3]
# Изменённый массив с повторяющимися данными
print(b)
# [[1 2 3 1]
# [2 3 1 2]]Объединение массивов
NumPy позволяет нам «наслаивать» массивы друг на друга и соединять их с помощью функций vstack и hstack:
v1 = np.array([1, 2, 3])
v2 = np.array([9, 8, 7])
v3 = np.vstack([v1, v2])
print(v3)
# Out:
# [[1 2 3]
# [9 8 7]]Здесь мы создали двумерный массив из двух векторов одинакового размера, которые «поставили» друг на друга. То же самое можно сделать и горизонтально:
h1 = np.ones((2, 4))
h2 = np.zeros((2, 2))
h3 = np.hstack((h1, h2))
print(h3)
# Out:
# [[1. 1. 1. 1. 0. 0.]
# [1. 1. 1. 1. 0. 0.]]К массиву из единиц справа присоединился массив из нулей. Главное — чтобы количество строк было у обоих одинаковым, иначе вылезет ошибка:
h1 = np.ones((2, 4))
h2 = np.zeros((3, 2))
h3 = np.hstack((h1, h2))
# Out:
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# File "<__array_function__ internals>", line 5, in hstack
# File "/Users/Dmitry/opt/anaconda3/lib/python3.9/site-packages/numpy/core/shape_base.py", line 345, in hstack
# return _nx.concatenate(arrs, 1)
# File "<__array_function__ internals>", line 5, in concatenate
# ValueError: all the input array dimensions for the concatenation axis must match exactly, but along dimension 0, the array at index 0 has size 2 and the array at index 1 has size 3Эта ошибка говорит, что количество строк не совпадает.
Для объединения трёхмерных массивов удобно использовать функцию dstack. Она принимает два одинаковых по размеру массива и объединяет их вдоль третьей оси:
a = np.array([[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]])
b = np.array([[[25, 26, 27, 28],
[29, 30, 31, 32],
[33, 34, 35, 36]],
[[37, 38, 39, 40],
[41, 42, 43, 44],
[45, 46, 47, 48]]])
result = np.dstack((a, b))
print("Shape of result:", result.shape)
# Shape of result: (2, 3, 8)
print("Resulting array:\n", result)
# Resulting array:
# [[[ 1 2 3 4 25 26 27 28]
# [ 5 6 7 8 29 30 31 32]
# [ 9 10 11 12 33 34 35 36]]
# [[13 14 15 16 37 38 39 40]
# [17 18 19 20 41 42 43 44]
# [21 22 23 24 45 46 47 48]]]Мы объединили переменные a и b по третьей оси — взяли элементы из обоих массивов и расположили их вдоль новой оси. В результате образовался новый массив с увеличенной третьей размерностью.
Для объединения массивов по новой оси подойдёт функция stack:
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
result = np.stack((a, b), axis=0)
print(result)
# Out:
# [[[1 2]
# [3 4]]
# [[5 6]
# [7 8]]]
result = np.stack((a, b), axis=1)
print(result)
# Out:
# [[[1 2]
# [5 6]]
# [[3 4]
# [7 8]]]Здесь мы создали новую первую ось и по ней объединили массивы. После мы выполнили объединение по второй оси. То есть функция stack позволяет нам добавлять измерение в любом месте, где потребуется.
В первом случае мы добавили новую ось перед существующими осями, создав новую ось 0. Предыдущая ось 0 стала осью 1. Таким образом, мы создали трёхмерный массив, где новая ось 0 имеет размер 2, поскольку мы объединили два массива. Оставшиеся оси сохранили свои размеры.
Во втором случае мы добавили новую ось в середину. Ось 0 осталась неизменной, а новая ось 1 была создана для объединения элементов вдоль предыдущей оси 1, которая теперь стала осью 2. Таким образом, мы создали трёхмерный массив, где новая ось 1 имеет размер 2.
Когда мы используем функцию stack, предыдущие оси сохраняют свои позиции и размеры, но их индексы увеличиваются на единицу, чтобы освободить место для новой оси.
Перестановка осей и транспонирование
Оси массива можно менять местами. Это может быть полезно, если нужно повернуть изображение. Один из частных случаев перестановки осей называется транспонированием — это когда строки и столбцы матрицы меняются местами. Для выполнения транспонирования есть метод transpose:
a = np.array([[1, 2, 3], [4, 5, 6]])
a_transposed = a.transpose()
print(a_transposed)
# Выводим транспонированную матрицу a:
# [[1 4]
# [2 5]
# [3 6]]
print(a.shape)
# Выводим форму исходной матрицы a:
# (2, 3)
print(a_transposed.shape)
# Выводим форму транспонированной матрицы a_transposed:
# (3, 2)Вместо метода transpose для транспонирования матрицы можно использовать атрибут T. Это сделает код более компактным и читаемым:
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a.T)
# Выводим транспонированную матрицу a:
# [[1 4]
# [2 5]
# [3 6]]
print(a.shape)
# Выводим форму исходной матрицы a:
# (2, 3)
print(a.T.shape)
# Выводим форму транспонированной матрицы a.T:
# (3, 2)Методу transpose можно указать порядок индексов осей для перестановки их значений. Это удобно, если размерность массива включает более двух осей.
# Создаём исходный трёхмерный массив
original_array = np.array([[[1, 2, 3], [4, 5, 6]]])
# Транспонируем исходный массив с помощью перестановок осей
transposed_array = original_array.transpose(1, 2, 0)
# Первая ось (axis 0 в исходном массиве) становится третьей осью (axis 2 в транспонированном массиве)
# Вторая ось (axis 1 в исходном массиве) становится первой осью (axis 0 в транспонированном массиве)
# Третья ось (axis 2 в исходном массиве) становится второй осью (axis 1 в транспонированном массиве)
# Выводим транспонированный массив
print(transposed_array)
# [[[1]
# [2]
# [3]]
# [[4]
# [5]
# [6]]]
# Выводим форму (shape) исходного массива
print(original_array.shape)
# (1, 2, 3)
# Выводим форму (shape) транспонированного массива
print(transposed_array.shape)
# (2, 3, 1)Дополнительные возможности
NumPy поддерживает и другие функции, которые применяются реже, но знать о них полезно. Например, одна из таких функций — чтение файлов с жёсткого диска.
Чтение данных из файла. Допустим, у нас есть файл data.txt с таким содержимым:
1,2,3,5,6,7
8,1,4,2,6,4
9,0,1,7,3,4Мы можем записать числа в NumPy-массив с помощью функции genfromtxt:
filedata = np.genfromtxt('data.txt', delimiter=',')
filedata = filedata.astype('int32')
print(filedata)
# Out:
# [[1 2 3 5 6 7]
# [8 1 4 2 6 4]
# [9 0 1 7 3 4]]Сначала мы достали данные из файла data.txt через функцию genfromtxt. В ней нужно указать считываемый файл, а затем разделитель — чтобы NumPy понимал, где начинаются и заканчиваются числа. У нас разделителем будет ,.
Затем нам нужно привести числа к формату int32 с помощью функции astype, передав в неё нужный нам тип.
Булевы выражения. Ещё одна из возможностей NumPy — булевы выражения для элементов массива. Они позволяют узнать, какие элементы отвечают определённым условиям — например, больше ли каждое число массива 50.
Допустим, у нас есть массив a и мы хотим проверить, действительно ли все его элементы больше 5:
a = np.array([[1, 5, 8], [3, 4, 2]])
print(a > 5)
# Out:
# [[False False True]
# [False False False]]На выходе — массив с «ответом» для каждого элемента: больше ли он числа 5. Если меньше или равно, то стоит False, иначе — True.
С помощью булевых выражений можно составлять и более сложные конструкции — например, создавать новые массивы из элементов, которые отвечают определённым условиям:
a = np.array([[1, 5, 8], [3, 4, 2], [2, 6, 7]])
print(a[a > 3])
# [5 8 4 6 7]Мы получили вектор, состоящий из элементов массива a, которые больше трёх.
Что важно запомнить
- NumPy — это библиотека для эффективной работы с массивами любого размера. Она достигает высокой производительности, потому что написана частично на C и C++ и в ней соблюдается принцип локальности — она хранит все элементы последовательно в одном месте.
- Перед тем как использовать NumPy в коде, его нужно подключить с помощью команды import numpy as np.
- Основа NumPy — массив. Чтобы его создать, нужно использовать функцию array и передать туда список в качестве первого аргумента. Вторым аргументом через dtype можно указать тип для всех элементов — например, int16 или float32. По умолчанию для целых чисел указывается int32, а для десятичных — float64.
- Функция ndim позволяет узнать количество измерений; shape — его структуру (сколько столбцов и строк); dtype — какой тип у элементов; size — количество элементов; itemsize — сколько байтов занимает один элемент; nbytes — сколько всего памяти занимает массив.
- К элементам можно обращаться с помощью оператора [], где указываются индексы нужного элемента. Важно помнить, что индексация начинается с нуля. А ещё в NumPy можно выбирать сразу целые строки или столбцы с помощью оператора : и его продвинутой версии — начальный_индекс:конечный_индекс:шаг.
- Функции zeros, ones, full, random.rand, random.randint, identity и eye помогают быстро создать массивы любого размера с заполненными элементами.
- Все арифметические операции, которые доступны в Python, применимы и к массивам NumPy. Главное — помнить, что операции проводятся поэлементно. А для сложных операций, таких как вычисление производной, также есть свои функции.
- Для статистических операций есть агрегатные функции. Они позволяют работать как с целым массивом, так и с его осями.
- NumPy-массивы нельзя просто присвоить другой переменной, чтобы скопировать. Для этого существует функция copy. А чтобы поменять структуру данных, можно применить функции reshape, vstack и hstack.
- Ещё в NumPy есть дополнительные функции — например, чтение из файла с помощью genfromtxt и булевы выражения, которые позволяют выбирать элементы из набора данных по заданным условиям.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!
Data Science с нуля: пробуем профессии на практике за 5 дней
Вы разберётесь в трёх главных направлениях data science: машинном обучении, разработке на Python и визуализации данных. Решите, какая сфера вам ближе, и выполните 4 реальные задачи с данными.
Пройти бесплатно









