Дисперсия в статистике: теория, формулы, примеры

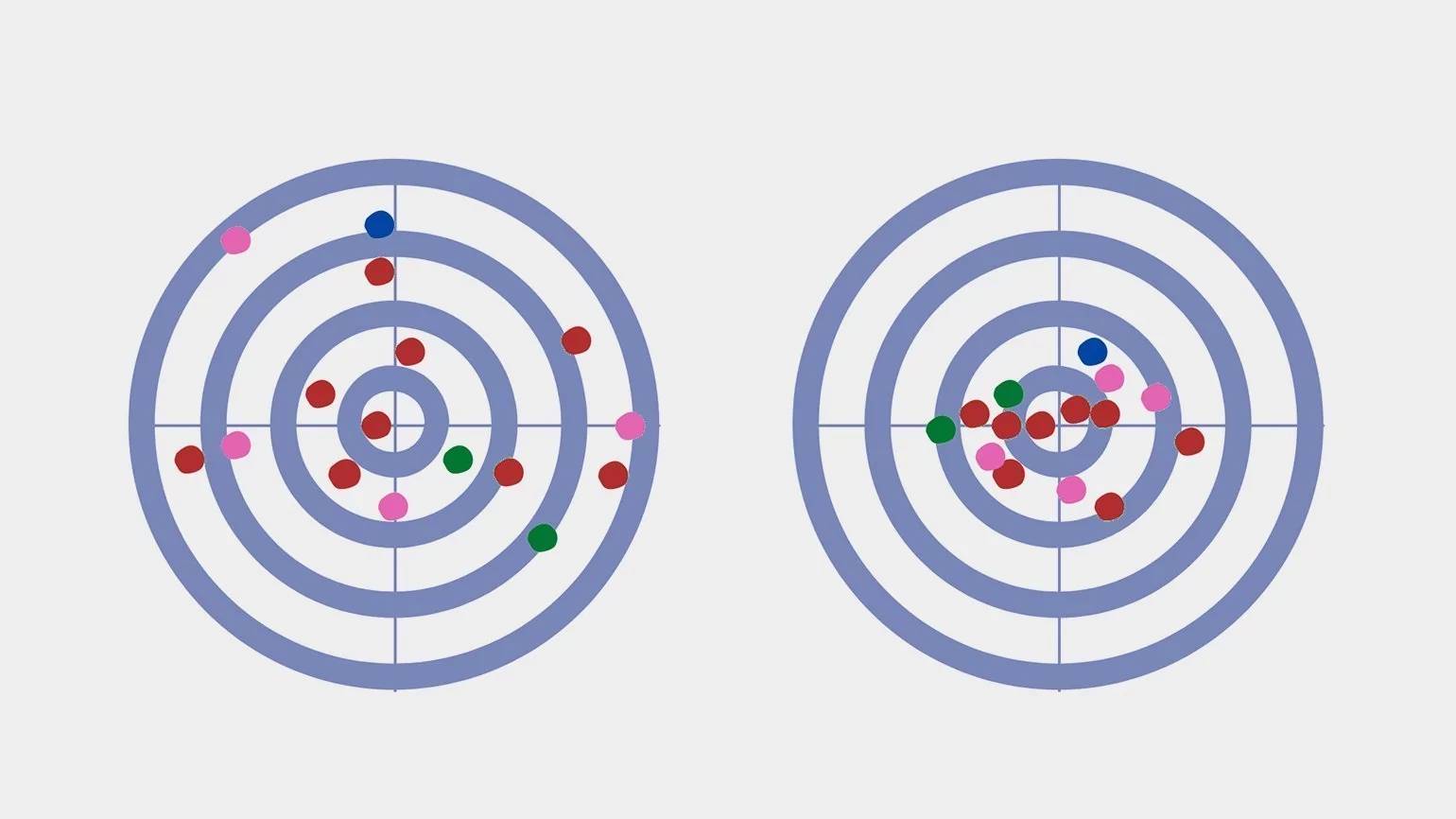
Чемпион по дартсу и математик зашли в паб, выпили по кружке пенного и начали бросать дротики. Математик заметил, что у бросков чемпиона низкая дисперсия. Давайте разберёмся и выясним:

• что такое дисперсия;
• где её применяют;
• как вычисляют;
• как она связана с другими статистическими показателями.

Понятие и виды дисперсии

Дисперсия в статистике — это показатель разброса данных вокруг их среднего значения. Высокая дисперсия указывает на большой разброс данных, а низкая — на их близость друг к другу. Рассмотрим примеры:

• 1, 2, 3, 4, 5 — числа находятся в пределах ±2 от среднего значения 3, поэтому дисперсия низкая;
• 13, 25, 976, 90, 120 713 — здесь дисперсия высокая, так как разница между наименьшим и наибольшим числом превышает 120 000.

Дисперсия случайной величины позволяет оценить уровень отклонения данных от их среднего значения. Допустим, средний балл на экзамене 75 из 100. Зная дисперсию, можно определить вероятность того, что конкретный студент получит результат, значительно отличающийся от 75 баллов:

• при высокой дисперсии баллы студентов будут сильно различаться, что увеличивает вероятность отклонений;
• при низкой дисперсии баллы близки к среднему значению, поэтому вероятность значительных отклонений небольшая.

Дисперсия бывает выборочной и генеральной. Выборочная вычисляется на основе части совокупности. Например, для оценки уровня холестерина в городе достаточно провести исследование на нескольких тысячах жителей. Всё население обследовать не нужно.

Генеральная рассчитывается для всей совокупности данных, когда известны значения всех элементов. То есть мы можем определить генеральную дисперсию для результатов ЕГЭ по математике в регионе, если известны баллы всех выпускников.

Читайте также:

Основы анализа данных для начинающих

Примеры использования

Дисперсия применяется в экономике, социологии, инвестициях и других областях, где важно анализировать и оценивать данные.

В экономике она используется для анализа доходов, расходов, цен на товары и других финансовых показателей. Например, если компания анализирует свои доходы по сезонам, малая дисперсия укажет на стабильность доходов, а высокая — на значительные колебания. Аналитики могут использовать эту информацию для планирования бюджета и разработки стратегии ценообразования.

Читайте также:

Финансовый анализ предприятия: стартовый гайд для тех, кто хочет быстро разобраться в теме

В социологических исследованиях с помощью дисперсии можно проанализировать распределение ответов при проведении опросов и выявлять степень вариации в мнениях участников. Например, если исследуется удовлетворённость сотрудников в отношении рабочего времени, то высокая дисперсия в ответах указывает на значительное разнообразие мнений. Это может помочь выявить группы с низким уровнем удовлетворённости и разработать меры по улучшению условий труда.

Читайте также:

Боюсь, что сотрудники крадут рабочее время. Пора ставить систему удалённого контроля?

В финансах дисперсия помогает оценивать риски инвестиций. Так, высокая дисперсия доходности активов указывает на повышенные риски и волатильность. Например, акции технологических компаний могут иметь большую дисперсию по сравнению с облигациями, что делает их покупку более рискованной. Инвесторы могут использовать эту информацию для создания сбалансированного портфеля, в котором риски будут минимизированы за счёт диверсификации активов.

Читайте также:

Инвестиции для начинающих: с чего начать и что изучить, чтобы получать стабильный доход

С дисперсией обычно работают учёные, статистики, аналитики, ML-инженеры и другие специалисты:

• Учёные используют её для анализа результатов экспериментов. Например, в медицинских исследованиях она помогает оценить, насколько различаются реакции пациентов на лечение и насколько эффективно оно работает в целом.
• Статистикам дисперсия нужна для анализа данных и построения надёжных моделей. Она помогает оценить точность модели прогнозирования спроса на товары, определяя, насколько предсказанные значения соответствуют фактическим.
• Аналитикам она помогает оценивать стабильность и эффективность бизнес-процессов. Например, можно проанализировать продажи по регионам, чтобы выявить успешные и проблемные зоны для расширения бизнеса.
• ML-инженеры используют дисперсию в машинном обучении для оценки разброса предсказаний моделей. Например, в модели классификации высокий разброс указывает на возможные ошибки в обучении модели и неправильное отображение данных.

Формулы и порядок расчёта дисперсии

Если известны все элементы совокупности данных, мы можем вычислить генеральную дисперсию (случайную величину):

Элементы формулы расчёта дисперсии случайной величины:

• σ² — генеральная дисперсия;
• N — количество элементов в совокупности;
• x_i​ — значение элементов;
• μ — среднее значение элементов.

Возьмём небольшой набор данных и поэтапно вычислим для него генеральную дисперсию: 2, 4, 4, 4, 5, 5, 7, 9.

Шаг №1. Сложим все значения нашего набора данных и разделим их на количество элементов, чтобы вычислить среднее значение:

Шаг №2. Для каждого значения вычтем среднее и возведём результат в квадрат, чтобы получить отклонение:

Результаты вычислений:

• (2 − 5)² = (−3)² = 9;
• (4 − 5)² = (−1)² = 1;
• (4 − 5)² = (−1)² = 1;
• (4 − 5)² = (−1)² = 1;
• (5 − 5)² = (0)² = 0;
• (5 − 5)² = (0)² = 0;
• (7 − 5)² = (2)² = 4;
• (9 − 5)² = (4)² = 16.

Шаг №3. Сложим полученные квадраты отклонений и разделим их на количество элементов:

Мы получили значение генеральной дисперсии, равное 4.

Если у нас есть только часть совокупности данных, мы можем использовать формулу выборочной дисперсии:

Элементы формулы расчёта дисперсии ряда чисел:

• s² — выборочная дисперсия;
• n — количество элементов в выборке;
• x_i​ — значение каждого элемента;
• x̅ — среднее значение выборки.

Порядок расчёта выборочной дисперсии почти не отличается от генеральной. Разница лишь в том, что в формуле выборочной дисперсии используется корректировка на размер выборки n − 1, а в генеральной дисперсии — общее количество элементов N.

Читайте также:

Математика в жизни: где нужна и как избежать

Связь дисперсии с другими статистическими показателями

Среднее арифметическое, стандартное отклонение и коэффициент вариации — это показатели, которые вместе с дисперсией помогают оценить разброс данных относительно их центрального значения.

Среднее арифметическое — это сумма всех значений в наборе данных, делённая на их количество. Оно служит основой для расчёта дисперсии, поскольку показывает, насколько значения отклоняются от среднего.

Стандартное отклонение показывает, насколько значения в наборе данных отклоняются от среднего арифметического. Оно является квадратным корнем из дисперсии и выражается в тех же единицах, что и исходные данные. Благодаря этому стандартное отклонение удобнее для интерпретации в практических задачах, где важно легко оценить разброс данных. Например, в научной сфере оно помогает определять точность измерений или величину погрешностей в экспериментах.

В отличие от стандартного отклонения, дисперсия измеряется в квадратных единицах и поэтому чаще используется в теоретических и математических расчётах, где нужны точные статистические оценки.

Коэффициент вариации — это мера относительного разброса данных, выраженная в процентах. Он показывает, насколько данные варьируются по отношению к их среднему значению. Поскольку коэффициент вариации основан на дисперсии, он напрямую связан с ней: высокий коэффициент указывает на большую дисперсию, а низкий — на меньшую. Его часто используют для сравнения разброса данных между различными наборами или для оценки надёжности результатов в финансах, экономике, производственной сфере и других областях.

Читайте также:

7 базовых статистических понятий, необходимых дата-сайентисту

Дисперсия также связана с другими статистическими показателями, например асимметрией и эксцессом. Они помогают лучше понять форму распределения данных, но их сложнее интерпретировать.