Интерполяция, экстраполяция и аппроксимация: что это такое и где применяется
Рассказываем, как аналитики «причёсывают» данные.


Аналитикам и дата-сайентистам часто приходится работать с неоднородными данными. Например, история погодных измерений меняется неравномерно, и такую информацию тяжело обрабатывать. Для выравнивания данных исследователи используют математические методы аппроксимации, интерполяции и экстраполяции.
В этой статье рассказываем, как ими пользоваться, и на примерах показываем, как строить точные прогнозы.
Содержание
- Почему данные неоднородны и зачем их выравнивать
- Аппроксимация: выравниваем данные
- Интерполяция: ищем недостающие значения
- Экстраполяция: предсказываем будущее
Почему данные неоднородны и зачем их выравнивать
В учебниках и теоретических моделях поведение природных процессов часто описывается плавными графиками: температура меняется по синусоиде, скорость ветра — линейно, рост растений — по экспоненте. Однако в реальной жизни ни одно природное явление не соответствует строгому графику.
Посмотрим на реальные данные метеостанций Санкт-Петербурга. Температура воздуха изменяется следующим образом:
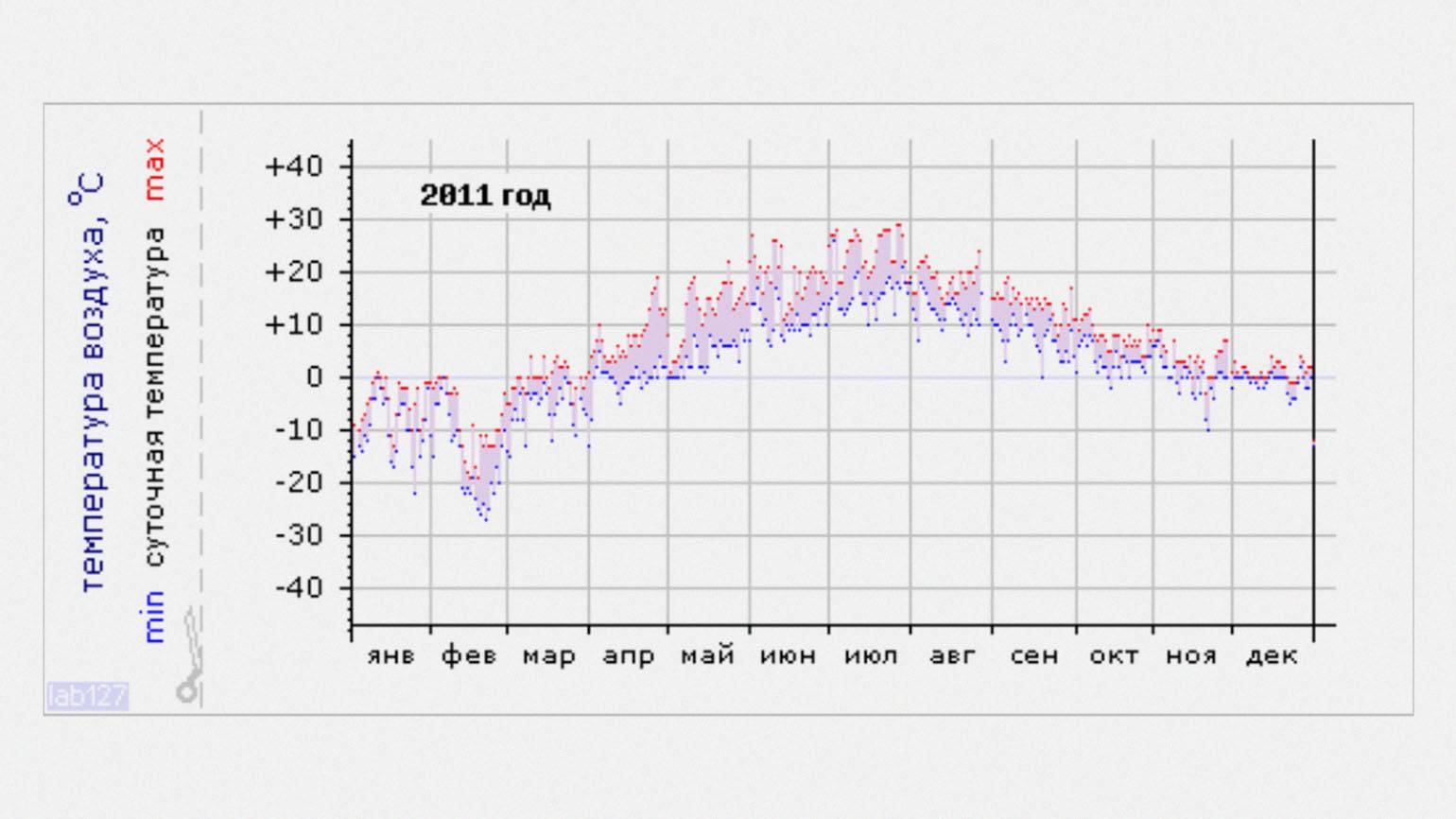
Скриншот: Thermo.Karelia / Skillbox Media
Кривая похожа на пилу: температура резко падает перед дождём, подпрыгивает, когда выглядывает солнце, и неспешно ползёт вниз ночью. На неё влияют одновременно облачность, ветер, прогретый днём асфальт, плотность городской застройки и десятки других факторов.
Чтобы находить закономерности в этом хаосе и делать прогнозы, синоптики и аналитики используют три математических инструмента: аппроксимацию, интерполяцию и экстраполяцию.
Давайте разберём на практике, как работает каждый из инструментов.
Аппроксимация: выравниваем данные
Аппроксимация — это приём, с помощью которого неравномерные или неполные данные описываются гладкой математической функцией, приближённо повторяющей их поведение. Проще говоря, исследователи берут неровный график и строят на его основе плавную копию. Так становится легче анализировать поведение системы и строить прогнозы, даже если исходные измерения содержат помехи.
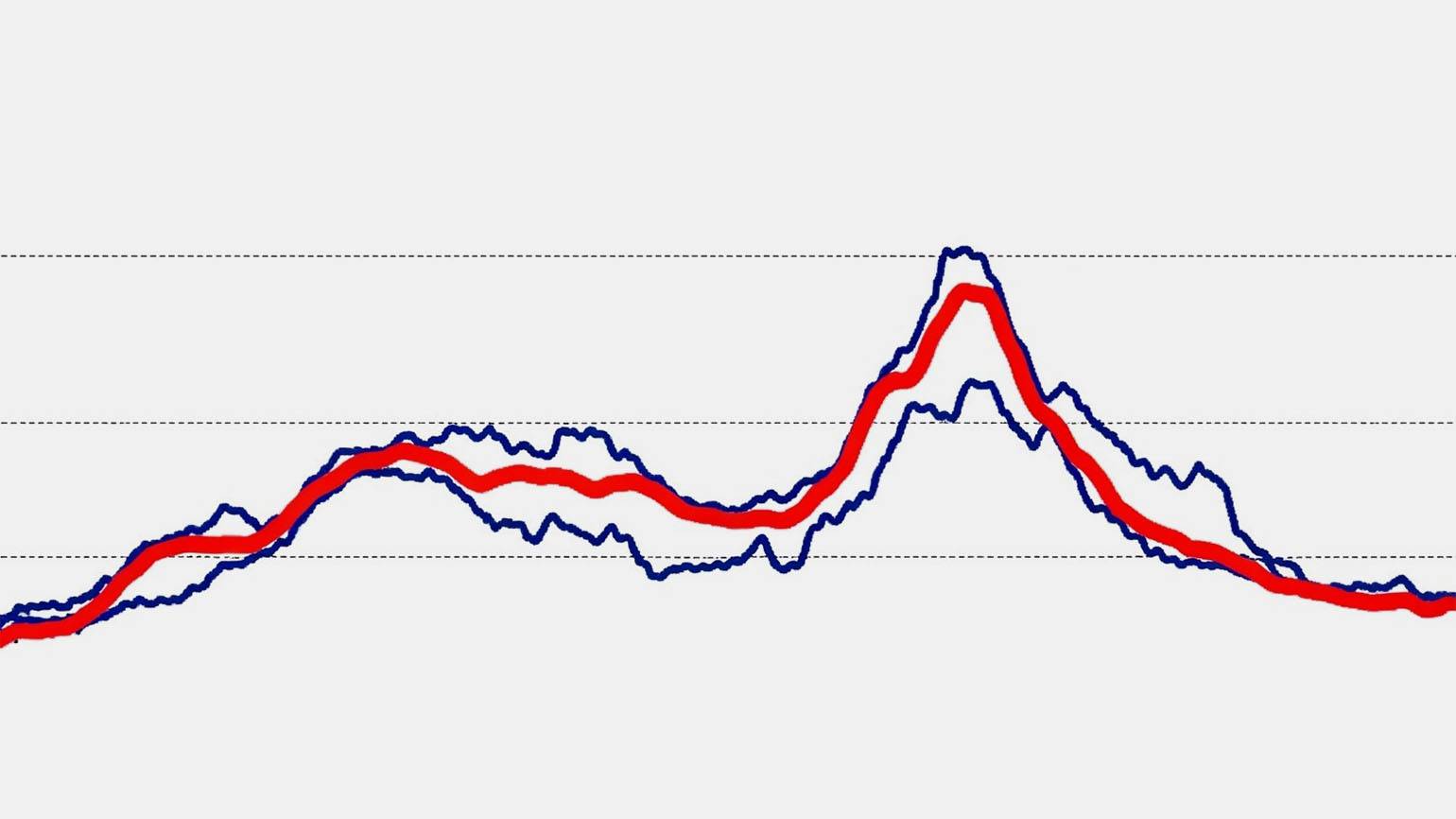
Скриншот: MS Excel / Skillbox Media
Аппроксимация особенно полезна, когда нужно выявить тренды, продлить данные дальше диапазона наблюдений или представить их в более наглядной форме.
Методы аппроксимации
Разберём основные методы аппроксимации данных.
Линейная аппроксимация. Самый простой способ сглаживания данных — провести прямую линию, которая проходит ближе всего ко всем точкам на графике.
Представьте, что вы замеряете температуру каждый час с 00:00 до 12:00. В итоге получится 13 точек, между которыми можно провести прямую. После этого сразу будет виден общий тренд — скажем, приближается полуденный максимум или всё идёт к вечернему похолоданию.
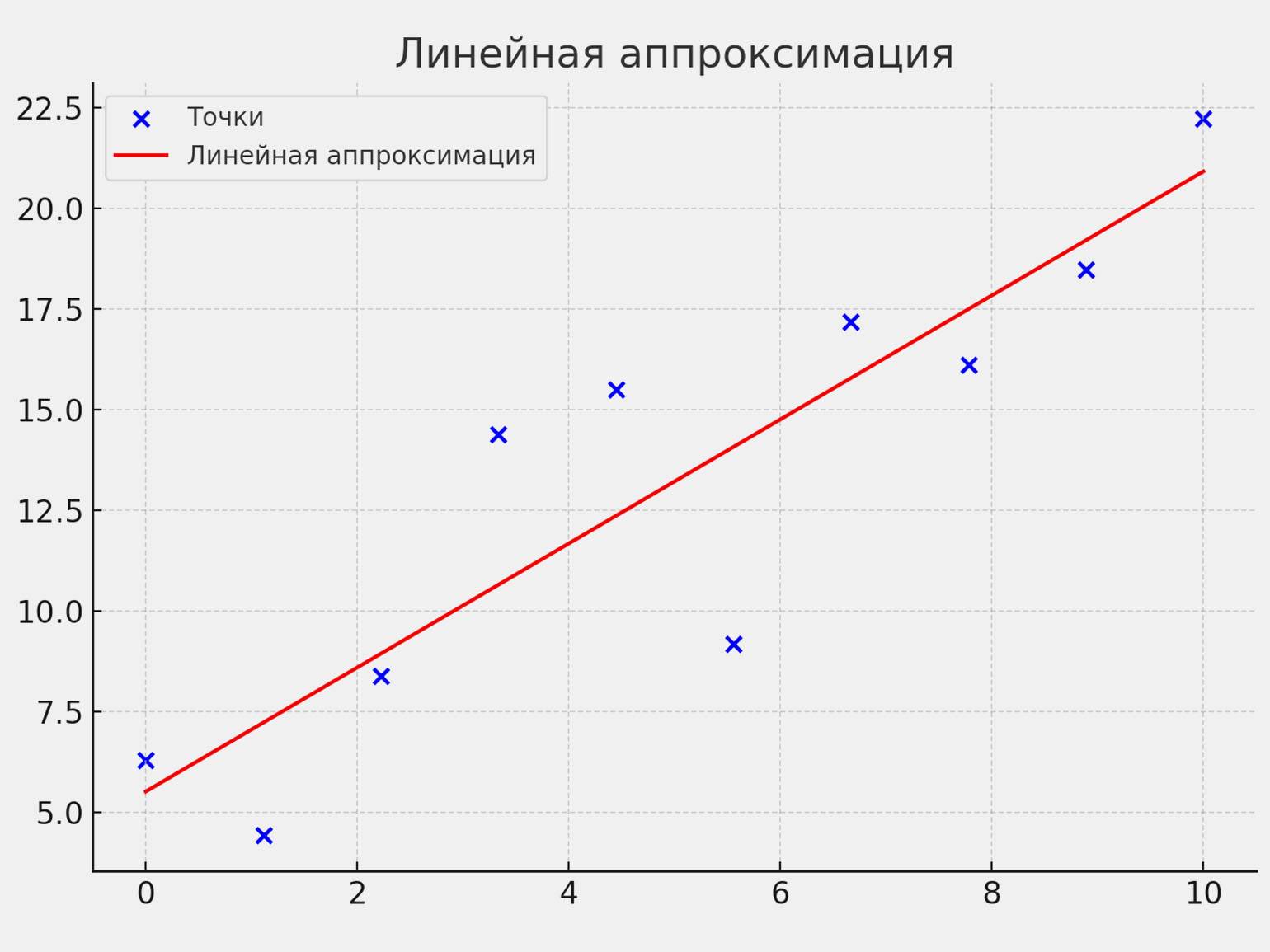
Скриншот: MS Excel / Skillbox Media
Полиномиальная аппроксимация. Если данных слишком много и линейная модель не справляется с выравниванием графика, можно использовать полином второй степени: y = ax2+ bx + c. Он позволяет построить параболу, которая будет точно огибать точки на графике.
К утру температура обычно снижается, а днём — растёт. Это поведение можно визуализировать, построив по точкам плавную кривую, отражающую суточный цикл. Это и есть пример полиномиальной аппроксимации.
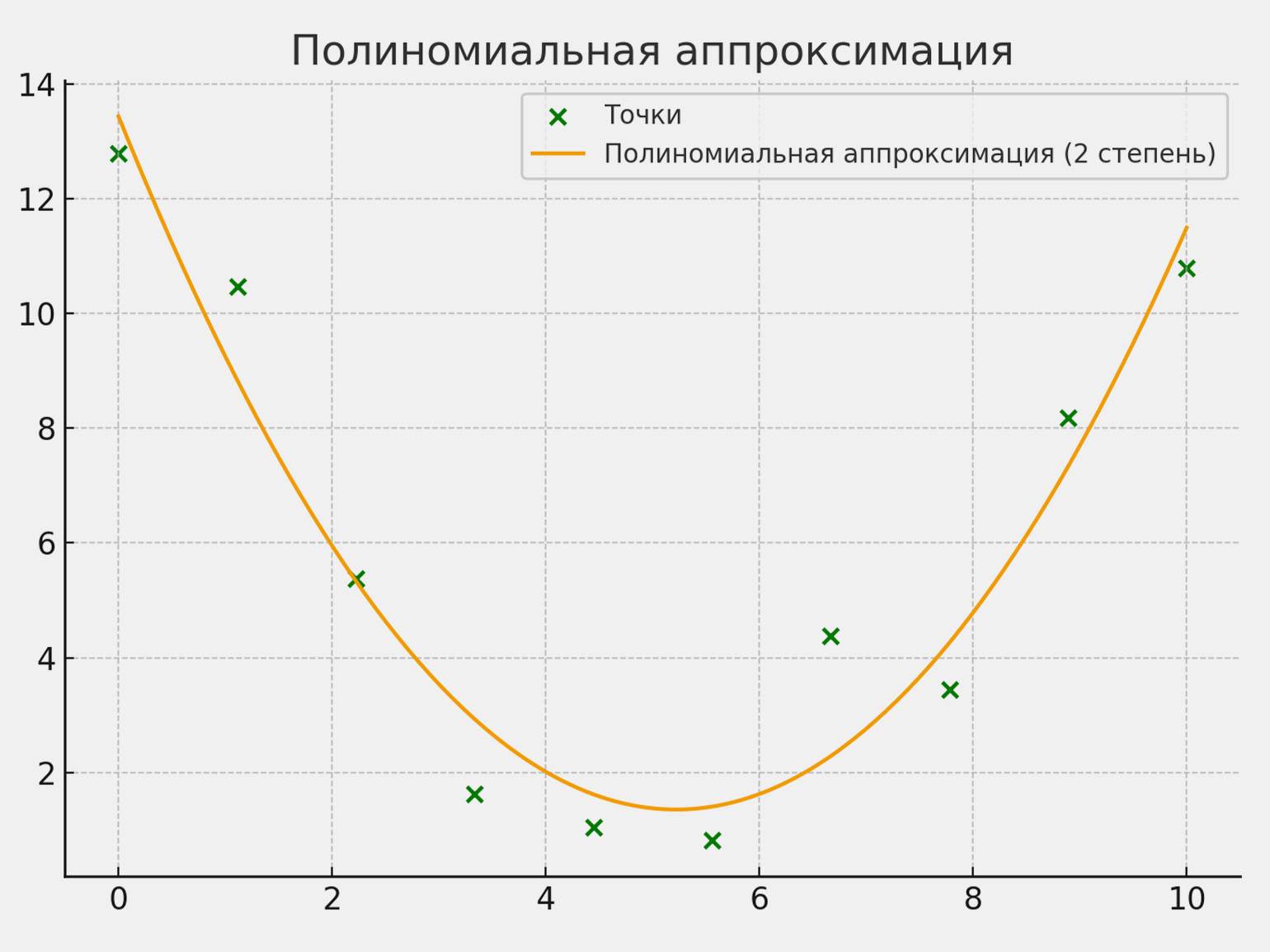
Скриншот: MS Excel / Skillbox Media
Сплайны. Суть метода в том, чтобы разбить данные на кусочки и провести аппроксимацию с каждым по отдельности. Благодаря этому можно получить гладкую кривую без резких изгибов и скачков, особенно на границах между кусками.
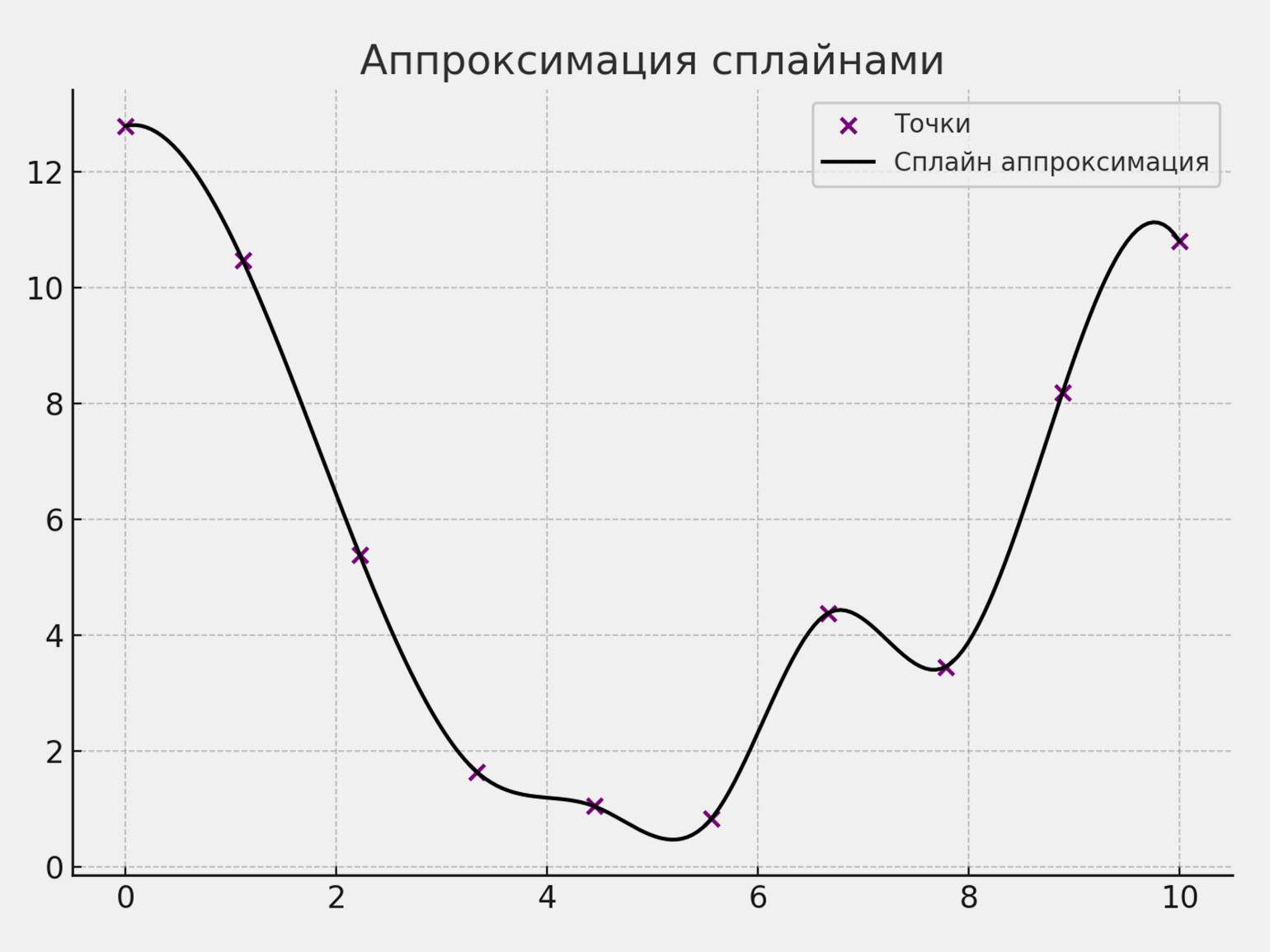
Скриншот: MS Excel / Skillbox Media
Интерполяция: ищем недостающие значения
Интерполяция — это способ оценить промежуточные значения функции на основе уже известных. Метод позволяет «заполнить пробелы», предположив, что между известными точками значения меняются по определённой закономерности.
Представьте, что у вас есть несколько точно измеренных точек температуры в течение дня:
- В 8:00 было 10 °C.
- В 12:00 было 15 °C.
- В 16:00 было 12 °C.
Вам нужно узнать, какая примерно температура была в 10 утра, хотя вы её не измеряли. Тут на помощь приходит интерполяция.
Методы интерполяции
Чаще всего для интерполяции данных используют следующие методы.
Линейная интерполяция. Если точек на графике мало, то мы можем предположить, что значение между ними меняется равномерно по этой прямой.
Например, мы измерили температуру воздуха в 8:00 и в 12:00 — это 10 °C и 15 °C соответственно. Чтобы узнать температуру в 10:00, мы предположим, что за эти 4 часа температура росла равномерно с 10 °C до 15 °C:
- Разница температур между 8 и 12 часами: 15 − 10 = 5 °C.
- С 8 до 10 утра прошло 2 часа.
- Предполагаемое увеличение температуры за 2 часа: 5 / 2 = 2,5 °C.
- Интерполированная температура в 10 утра: 10 + 2,5 = 12,5 °C.
Ближайший сосед. Вместо вычислений вы просто берёте значение ближайшей известной точки и используете его как приближённое для нужного момента. Этот способ интерполяции неточный и хорошо работает с небольшим набором данных.
Представьте, что вам нужно оценить температуру в 10:30. Ближайшая по времени точка — 12:00, где было 15 °C. Значит, предполагаем, что и в 10:30 температура составляла те же 15 °C.
Полиномиальная интерполяция. Если данных много, то через все известные точки можно провести параболу, плавно описывающую все точки. Этот метод даёт более гладкие и естественные кривые, чем, например, линейная интерполяция.
Допустим, у нас есть измерения температуры:
- 8:00 — 10 °C.
- 12:00 — 15 °C.
- 16:00 — 12 °C.
Можно построить параболу, которая проходит через эти три точки. Полученное уравнение позволит вычислить температуру в любой момент между 8:00 и 16:00.
Экстраполяция: предсказываем будущее
Если интерполяция помогает находить значения внутри диапазона известных точек, то экстраполяция — это метод оценки значений функции за пределами известных данных. Метод основан на предположении, что выявленные закономерности сохраняются и дальше.
Представьте: в 8:00 температура была 0 °C, а в 12:00 — уже 20 °C. Мы замечаем, что каждые два часа температура растёт на 5 °C. Тогда по этой логике можно предположить, что в 16:00 будет уже 30 °C, — это и есть экстраполяция.
Методы экстраполяции
Существуют различные методы экстраполяции, подходящие для определённых ситуаций. Расскажем про основные из них:
Линейная экстраполяция. Самый простой и наглядный метод. Мы продолжаем прямую линию, построенную по последним известным точкам, за пределы доступных данных. Подходит, если данные изменяются равномерно.
Это самый простой метод, который подходит, когда данные изменяются равномерно. Если график хаотичный, то линейная экстраполяция не подойдёт.
Полиномиальная экстраполяция. Этот способ предполагает, что данные можно аппроксимировать с помощью квадратичной или кубической функции. Построив полиномиальную модель, можно вычислить приближенные значения за пределами исходного диапазона.
Экстраполяция на основе кривых роста. Обычно реальные процессы не растут ровно по прямой линии, а могут ускоряться, замедляться, приближаться к какому-то пределу. В этих случаях применяют:
- Экспоненциальный рост — когда изменения вначале почти незаметны, а после резко увеличиваются. Например, когда при размножении бактерий каждые 20 минут их становится вдвое больше.
- Экспоненциальное затухание — когда значение убывает быстро в начале, а потом почти незаметно. Например, так остывает горячая кружка чая.
В экстраполяции по такой модели сначала подбирают функцию, наиболее точно описывающую известные данные, а затем эту функцию используют для прогнозов вне диапазона наблюдений.
Экстраполяция на основе машинного обучения. Если зависимость слишком сложная, а данных много, можно обучить модель (например, нейросеть), чтобы она сама находила закономерности и делала прогнозы. Такой подход используют для предсказания, например, погоды, цен на рынке или спроса в логистике.
Это самый мощный, но и самый ресурсоёмкий способ экстраполяции.
Что запомнить
- Аппроксимация — способ сгладить шумные или неполные данные, заменив их более простой математической моделью, чтобы выявить тренды и закономерности.
- Интерполяция — метод оценки промежуточных значений функции на основе уже известных точек. Используется, чтобы «заполнить пробелы» внутри диапазона наблюдений.
- Экстраполяция — метод прогнозирования значений за пределами известных данных. Работает, если предполагается, что тренд сохраняется.
- Линейные методы (прямая линия) подходят, когда данные меняются равномерно.
- Нелинейные модели (полиномы, экспоненты, логистические кривые) нужны, если процессы ускоряются, замедляются или выходят на предел.
- При выборе метода важно учитывать поведение данных: равномерность, периодичность, наличие трендов и шумов.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!