Задача: инвертируем бинарное дерево

Решаем задачи, которые дают программистам на собеседованиях в IT-компаниях. Сегодня инвертируем бинарное дерево.

Иллюстрация: Polina Vari для Skillbox Media

Дмитрий Зверев

Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.

Сергей Голицын

Senior Java Developer в Covalent Inc. и преподаватель. Больше семи лет в Java-разработке. В свободное время судит хакатоны и делится опытом с начинающими программистами. Пишет статьи для «Хабра» и Medium. Ведёт телеграм-каналы «Полезные ссылки около Java» и Cracking code interview.

Условие. Дан массив узлов бинарного дерева — root. Нужно инвертировать дерево и вернуть полученный массив. Инвертировать бинарное дерево — значит сделать так, чтобы слева от главного узла были значения больше него, а справа — меньше. Когда значения равны, их можно помещать с любой стороны.

Ввод и вывод. Пример 1

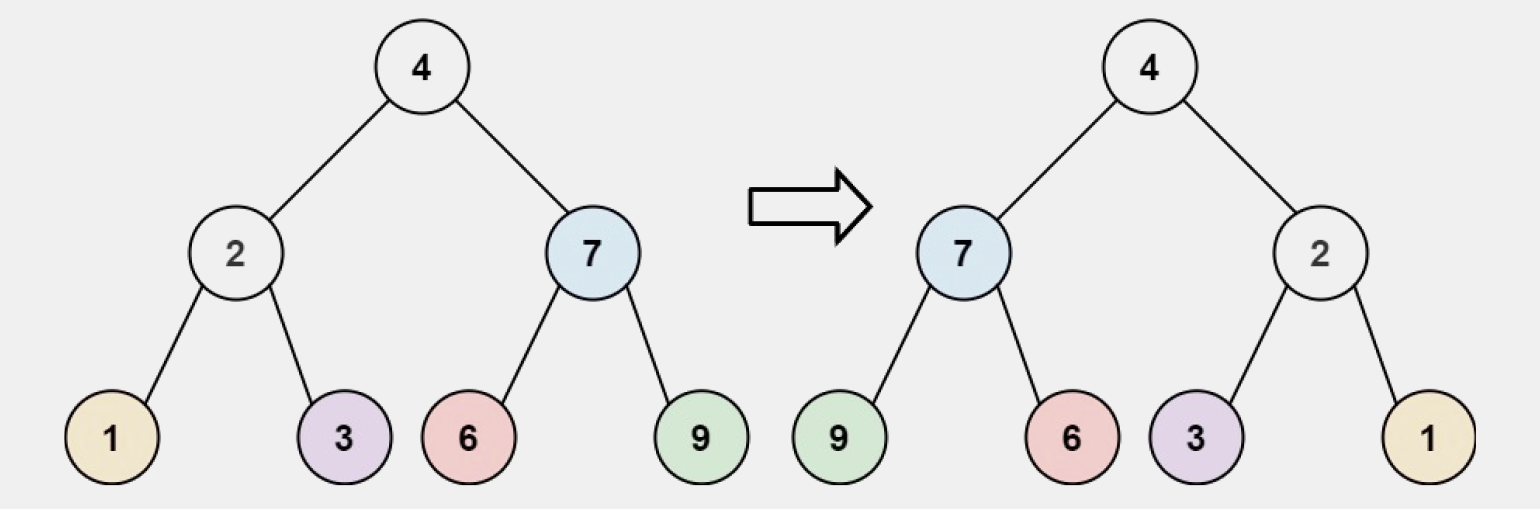
Ввод: root = [4,2,7,1,3,6,9]
Вывод: [4,7,2,9,6,3,1]

Ввод и вывод. Пример 2

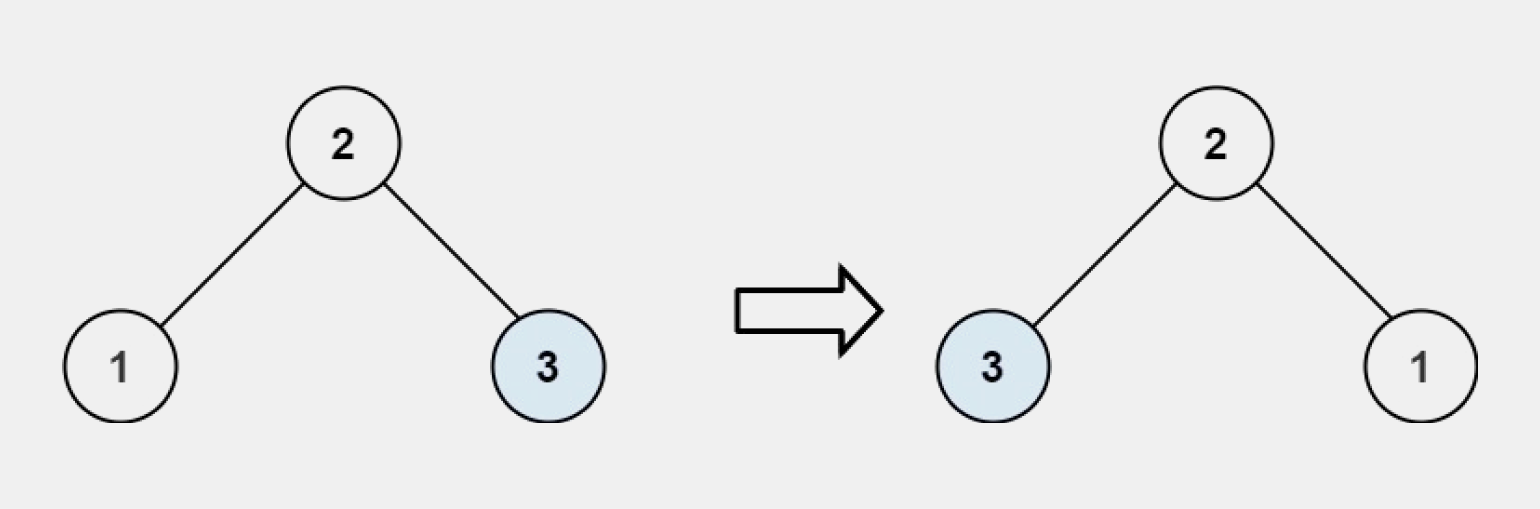
Ввод: root = [2,1,3]
Вывод: [2,3,1]

Ввод и вывод. Пример 3

Ввод: root = []
Вывод: []

Решить эту задачу самостоятельно и на разных языках программирования можно на LeetCode. Наше решение взято из Telegram-канала Сергея Cracking code interview.

Решение

Чтобы решить эту задачу, мы должны поменять все левые и правые элементы местами и сделать это в обратном порядке — с помощью рекурсии.

Начнём с самого верхнего узла и будем двигаться вниз — до самого нижнего. Каждый раз, когда мы заходим на очередной узел, меняем левый и правый элементы местами. А когда узлы закончатся, возвращаем полученный массив.

Полный алгоритм такой:

На входе мы получаем узел бинарного дерева — root.
Проверяем: если root — это пустой массив или null, то возвращаем null.
Если нет: вызываем рекурсию на левый узел, а затем на правый.
После того как обе рекурсии вернули результаты, меняем левый и правый узлы местами.
Возвращаем корень дерева.

Вот как этот алгоритм будет реализован на Java:

public TreeNode invertTree(TreeNode root) {
     
    if(root == null){
      return null;
    }
     
    TreeNode left = invertTree(root.left);
    TreeNode right = invertTree(root.right);
     
    root.left = right;
    root.right = left;
    return root;
  }
}

Результаты

Временная сложность: O(n) — так как мы перебирали все элементы массива.

Ёмкостная сложность: O(1) — нам нужно заранее определённое количество места в памяти (максимальный размер памяти — размер массива бинарного дерева).

Читайте также: