Великая тройка: алгоритмы сортировки, которые точно пригодятся на собеседовании
Да кто такой этот ваш Bubble Sort?! Валерий Жила доступно рассказал о базовых алгоритмах сортировки и сравнил их характеристики.



Валерий Жила
Software engineer, разрабатывает системы управления городской инфраструктурой для мегаполисов по всему миру. Основная деятельность: backend, database engineering. Ведёт твиттер @ValeriiZhyla.
Сегодня я расскажу простым языком о Bubble Sort, Insertion Sort и Selection Sort. Я покажу, какие идеи лежат в основе этих сортировок и продемонстрирую их сильные и слабые стороны. Мы разберём алгоритмы по шагам, рассмотрим их простые версии и даже немного улучшим.
Дальнейший рассказ подразумевает, что вас не смущают такие фразы, как «сложность worst-case-алгоритма по времени равна O(n^2)». Иногда Time Complexity я буду называть «сложностью по времени», а Space Complexity — «сложностью по памяти».
Если вы новичок в теории алгоритмов, сначала прочитайте статью Валерия о Big O Notation. В ней он человеческим языком рассказал, что такое алгоритмическая сложность и как её считать.
На какие вопросы нужно ответить перед сортировкой массива
Давайте подумаем, на какие вопросы нужно ответить программисту, который собирается отсортировать элементы массива.
Вопрос первый. Отсортировать оригинальный массив или его копию?
Сортировка оригинала. Недостаток этого решения в том, что мы потеряем изначальный массив. Представляет ли он ценность — зависит от ситуации. Тем не менее это лишний побочный эффект (side effect) работы алгоритма.
Зато нам не придётся выделять память под копию массива. Иначе Space Complexity выросла бы до O(n). А так имеем O(1) памяти. Красота! Кроме того, массив не придётся копировать, а значит, мы сэкономим O(n) у Time Complexity.
Сортировка копии (out-of-place). Здесь всё наоборот: никаких сторонних эффектов, зато сложность алгоритма по памяти и времени вырастает до O(n). Забегая вперёд, скажу, что лишнее O(n) времени на копирование не так уж и страшно по сравнению со временем на саму сортировку, которая сожрёт намного больше. А вот дополнительные O(n) памяти — это серьёзный аргумент против out-of-place-алгоритмов.

Вопрос второй. Как поменять элементы массива местами?
Напишем функцию, которая эффективно переставляет два элемента местами по их индексам:
def swap(int[] arr, fst_idx, snd_idx):
int temp = arr[frst_idx]
arr[frst_idx] = arr[snd_idx]
arr[snd_idx] = tempФункция swap() получает массив и два индекса. Сначала она сохраняет копию элемента с индексом frst_idx в переменную temp. Затем записывает в элемент с индексом frst_idx содержимое элемента с индексом snd_idx. В этот момент содержимое обоих элементов одинаковое, а оригинальное значение frst_idx хранится в temp. Поэтому мы записываем его в ячейку snd_idx.
Приведённые выше идентификаторы довольно часто используются в реальных программах. Временные значения хранят в переменной temp (сокращение от temporary, то есть «временный»). fst — это сокращение от first, snd — от second. А слово «индекс» часто обозначают idx, потому что мы, программисты, не любим тратить буквы впустую :)
Вопрос третий, ключевой. Как правильно упорядочить массив?
Было бы неплохо начать со сравнения элементов между собой. «Сравнивать-то можно, а что делать дальше?» — спросите вы. Как что? Менять их местами! Кажется, это действительно поможет навести порядок в нашем массиве… ну, или снизить уровень хаоса :)
Статья написана на основе треда Валерия в Twitter.
Будем сравнивать элементы с соседними индексами. Если значение левого элемента больше правого — поменяем их местами. Произвольный индекс массива назовём i. Тогда у правого соседа будет индекс i + 1. Теперь реализуем эту мысль в виде небольшого блока кода:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)Этот код — замечательная отправная точка для сортировки массива от меньшего элемента к большему. Но его нужно довести до ума.
Сперва применим описанные команды к каждому элементу массива. Разумеется, кроме последнего — иначе наша программа вышла бы за пределы массива и выдала ошибку. Отсюда и n - 1:
int n = arr.length
for i in 0..n-1:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)Этот код не отсортирует наш массив, но сделает его более упорядоченным. Вот небольшой пример его работы:

Обратите внимание: почти все элементы массива сместились в нужную сторону, а самый большой (9) оказался в крайней правой ячейке! На каждой итерации он менялся местами с соседом справа и «всплыл на поверхность».
Исполним наш код ещё несколько раз:
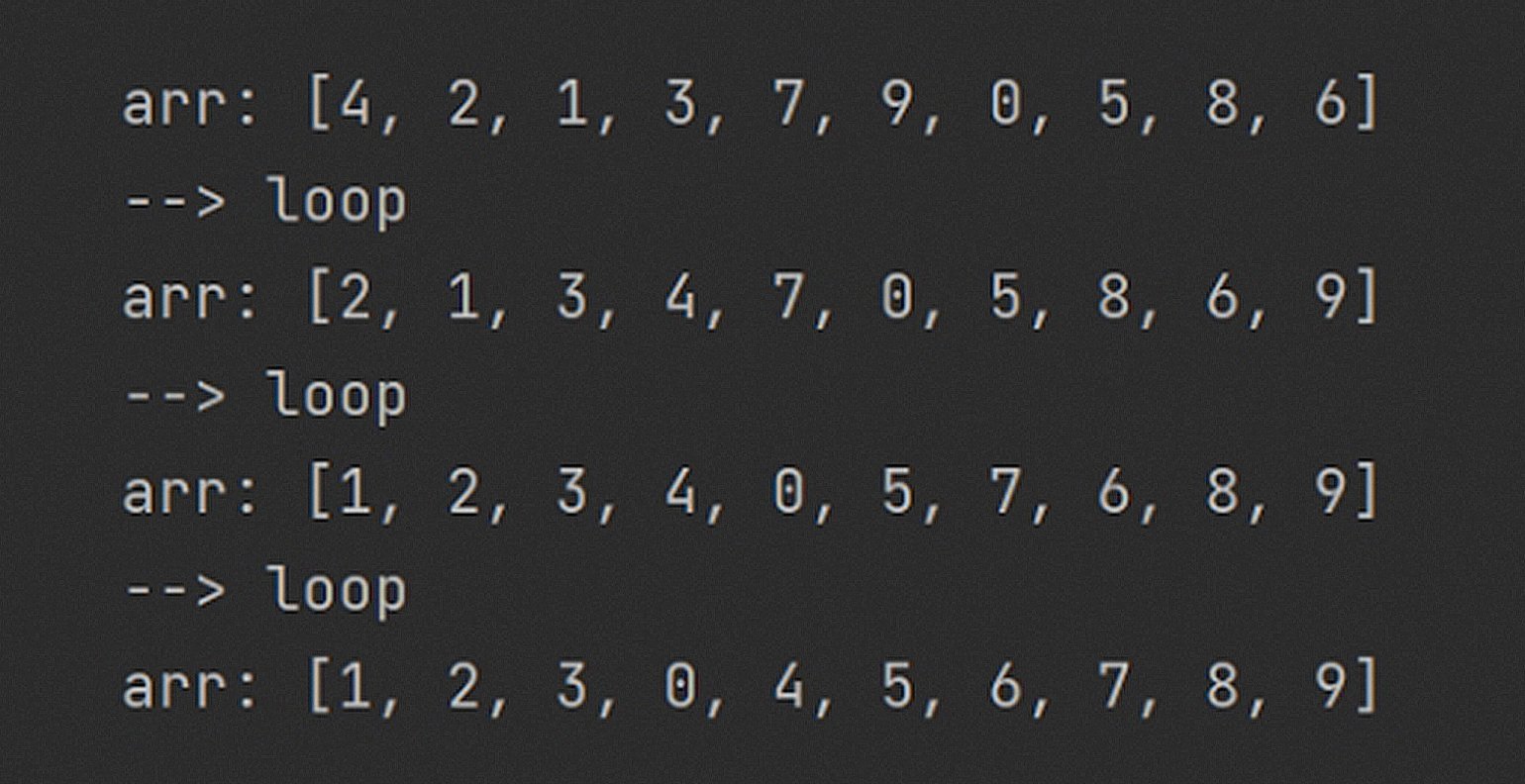
Всего за три прохода данные заметно упорядочились. Каждый виток гарантирует всплывание одного из элементов: на первом шаге число 9 встало на своё место, на втором — 8, а затем, по счастливой случайности, — сразу четыре элемента.
Сколько нужно сделать таких перестановок, чтобы гарантированно отсортировать массив? Если каждый проход выталкивает минимум один элемент, то через n проходов мы точно получим отсортированный массив! Даже через n - 1, потому что у крайнего правого элемента останется только один вариант размещения.
int n = arr.length
for j in 0..n-1:
for i in 0..n-1:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)Великолепно! Мы только что получили первый алгоритм сортировки. Итерация за итерацией — большие числа «всплывают», а меньшие «тонут». Очень давно кто-то увидел в этом аналогию с пузырьками воздуха в воде, поэтому такая сортировка называется пузырьковой, или Bubble Sort.
Как работает Bubble Sort
Наша версия «пузырька» вышла максимально наивной: и в лучшем, и в худшем случае его сложность по времени равна O(n^2). Конечно, план надёжный как швейцарские часы, но его можно улучшить!
Мы знаем, что каждое выполнение внутреннего цикла гарантированно ставит на место один правый элемент. Значит, с каждым новым j можно сокращать диапазон прохода внутреннего цикла на единицу. Зачем трогать элементы, которые уже стоят на своих местах?
Поэтому в строке 3 добавляем смещение j:
int n = arr.length
for j in 0..n-1:
for i in 0..n-1-j:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)Уже лучше, но программа всё ещё делает много лишней работы. Ведь за одну итерацию может «всплыть» сразу несколько элементов. Как добиться, чтобы программа останавливалась, когда массив будет полностью отсортирован? А вот как:
int n = arr.length
int was_swapped = false
for j in 0..n-1:
was_swapped = false
for i in 0..n-1-j:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)
was_swapped = true
if was_swapped == false
break;Мы ввели новую переменную, которая в начале внешнего цикла устанавливается в false и после каждого свопа меняет значение на true.
Если внутренний цикл не сделает ни одного свопа, переменная сохранит значение false и прервёт внешний цикл. Теперь сложность Best Case стала равна O(n)!
Если программа работает с изначально отсортированным массивом, то потребуется лишь один проход внутреннего цикла — чтобы обнаружить отсутствие перестановок и прервать внешний цикл. Вот это уже смахивает на Bubble Sort, который и на собесе не стыдно нарисовать!
Облачим код в функцию и продолжим полёт нашей фантазии:
def bubble_sort(int[] arr)
int n = arr.length
int was_swapped = false
for j in 0..n-1:
was_swapped = false
for i in 0..n-1-j:
if arr[i] > arr[i + 1]:
swap(arr, i, i + 1)
was_swapped = true
if was_swapped == false
break
return arrВ таблице представлены значения Time Complexity для лучшего, среднего и худшего случаев входных данных, а также значение Space Complexity:
| Name | Bubble |
|---|---|
| Name | Bubble |
| Worst | O(n^2) |
| Average | O(n^2) |
| Best | O(n) |
| Space | O(1) |
Как работает Selection Sort
В основе пузырьковой сортировки — сравнение соседних элементов массива. А как ещё можно отсортировать массив? Начнём с небольшой воображаемой сцены.
Перед мальчиком (можете заменить на девочку) на столе хаотично лежат карточки с числами. Мальчик хочет разложить эти числа по возрастанию. Он находит карточку с самым маленьким числом и откладывает её на соседний стол. Затем он возвращается к перемешанным карточкам, находит очередное наименьшее число, забирает карточку и кладёт её на второй стол, справа от предыдущей.
Так, шаг за шагом, мальчик выстроит шеренгу из чисел. Несложно догадаться, что получившийся аналог массива будет отсортирован по возрастанию — слева лежит наименьшее число, справа — наибольшее. Примерно так работает наивная сортировка выбором, или Selection Sort. Давайте попробуем изобразить её в виде кода.
Нам понадобится функция для поиска индекса наименьшего элемента:
def find_min(int[] arr):
int current_min_idx = 0
int current_min_value = arr[0]
for i in 0..arr.length:
if (arr[i] < current_min_value):
current_min_value = arr[i]
current_min_idx = i
return current_min_idxМожно было бы обойтись без current_min_value, но я оставлю эту переменную для наглядности.
Суть find_min() предельно проста. Будем считать, что первый элемент массива — это текущий минимум, и поочерёдно сравним его с другими элементами. Если какой-нибудь элемент меньше текущего минимума, то обновим значение current_min_value.
При этом мы обусловимся, что в массиве arr есть хотя бы один элемент и все ячейки заполнены числами. В противном случае find_min() станет ещё более страшным :)
Ещё нам нужна функция, которая удаляет элемент из массива. Максимально простая функция, исключительно красоты ради:
def delete_element(int[] arr, int idx):
arr[idx] = nullИтак, приготовления завершены, и мы можем приступить к сортировке. Будем урезать оригинальный массив шаг за шагом, а результат выстраивать во втором массиве. Для этого сначала создадим пустой массив того же размера, что и оригинал.
А дальше реализуем шаги из нашего мысленного эксперимента в виде кода:
def native_selection_sort(int[] arr):
int n = arr.length
int[] sorted_arr = int[n] # пустой массив с n ячейками
for i in 0..n:
int idx_of_min_element = find_min(arr)
sorted_arr[i] = arr[idx_of_min_element]
delete_element(arr)
return sorted_arrКакие замечания могут возникнуть к этому алгоритму:
- Он ест слишком много памяти. Мы создаём отдельный массив под результат и получаем O(n) по памяти.
- В оригинальном массиве появляются дыры. Функция delete_element() создаёт пустые ячейки в arr, о которые споткнётся find_min().
- Высокая Time Complexity. Алгоритм явно не блещет скоростью исполнения — O(n^2) как в худшем, так и в лучшем случае.
Возникает резонный вопрос: что же делать? Сейчас может быть немного непонятно, но обещаю, что дальше всё встанет на свои места.
Вот код оптимальной Selection Sort. Он упорядочивает элементы сразу в arr, а не создаёт дополнительный массив:
def selection_sort(int[] arr):
int n = arr.length
for i in 0..n:
min_idx = find_min_between(arr, i + 1, n)
swap(arr, i, min_idx)
return arrКомпактно, правда? Я добавил функцию find_min_between(array, start_idx, end_idx). Она работает как уже знакомая find_min(array), только проходит не по всему массиву, а по отрезку между start_idx и end_idx. Функция swap(array, i, j) тоже в представлении не нуждается.
Теперь разберёмся, как работает улучшенная версия Selection Sort. Возьмём массив arr с десятью числами:

Пройдёмся по массиву несколько раз циклом из selection_sort() и посмотрим на состояние arr. Вот что мы получим:

Чтобы сохранять упорядоченные элементы в левой части массива arr, алгоритм использует барьер между отсортированной и неотсортированной частью. Этот барьер находится между элементами с индексами i и (i + 1).
В каждой итерации алгоритм ищет наименьшее значение в правой части (от i + 1 и до конца массива) и меняет его местами с элементом по индексу i. При i = 1 в отсортированной части массива будет только один элемент. При i = 2 — два.
Сделаем процесс чуть более наглядным. Добавим разделитель между элементами, по которым проходит граница между отсортированной и неотсортированной частями массива:
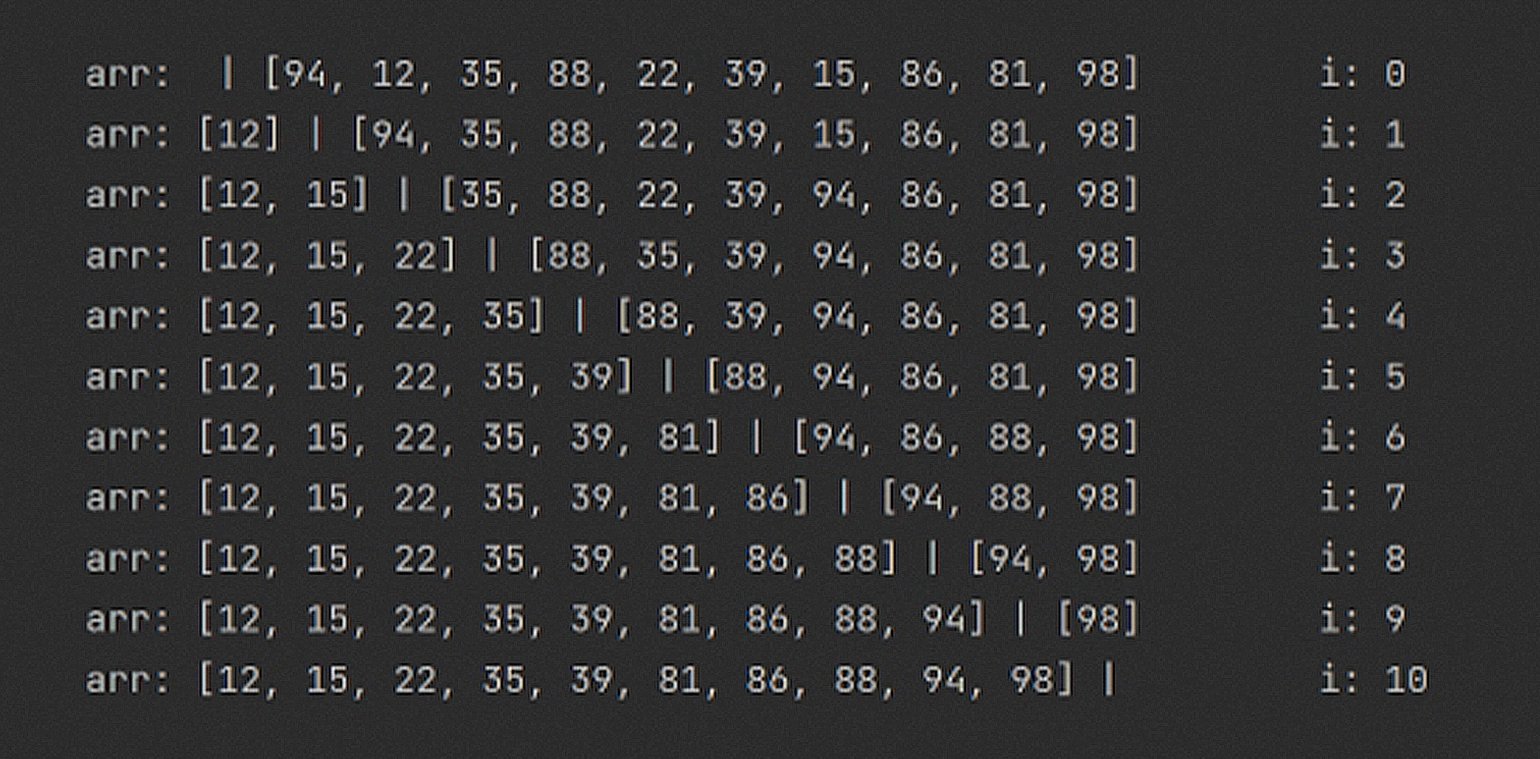
Обратите внимание: состояние arr показывается в конце каждой итерации. Первая строчка при i = 0, вторая при i = 1 и так далее.
Надеюсь, теперь идея Selection Sort кажется простой и естественной. Давайте взглянем на характеристики алгоритма.
С одной стороны, у такой реализации хорошая сложность по памяти O(1) за счёт использования левой части массива. С другой — поиск минимального элемента съедает O(n) времени и повторяется в каждом цикле (n раз). Поэтому мы получаем и Worst Case, и Best Case равные O(n^2), а это нехорошо.
Выходит, Bubble Sort быстрее, чем Selection Sort из-за Best Case O(n)? Тут как в известном анекдоте: есть один нюанс. В конце статьи мы ещё обсудим аспекты, которые не учитывает О-нотация.
Дополним нашу таблицу с характеристиками:
| Name | Bubble | Selection |
|---|---|---|
| Name | Bubble | Selection |
| Worst | O(n^2) | O(n^2) |
| Average | O(n^2) | O(n^2) |
| Best | O(n) | O(n^2) |
| Space | O(1) | O(1) |
Как работает Insertion Sort
Insertion Sort, она же сортировка вставками, очень похожа на Selection Sort. Я даже называю её «Selection Sort наоборот», потому что она действует по обратному принципу.
Напомню, что в Selection Sort мы искали наименьший элемент в правой части, переставляли его в конец левой и шли дальше. Самая дорогая операция в этом алгоритме — поиск наименьшего элемента.
В Insertion Sort мы тоже сохраняем упорядоченные элементы в исходном массиве. Только на этот раз из правой части берём первый попавшийся элемент и выбираем, куда его вставить в левой.
При этом левая часть массива всегда будет отсортирована. А это значит, что нам нужно лишь найти подходящее место, сдвинуть всех соседей справа на одну позицию правее и вставить новый элемент на освободившееся место.
Работа Insertion Sort немного напоминает толкучку в общественном транспорте. Боксёр-тяжеловес, который зайдёт в набитый трамвай, вероятно, спровоцирует движение всех пассажиров на полшага от выхода.
Рассмотрим пример такой вставки. У нас есть отсортированный массив из восьми чисел со свободной ячейкой в конце. Нужно добавить в этот массив число 5 на правильную позицию. Вот как будет выглядеть алгоритм:
int[] arr = [1, 2, 3, 4, 6, 7, 8, 9, _]
int key = 5
int element_to_move_idx = arr.length - 2
# arr[arr.length - 2] = 9
while (element_to_move_idx >= 0) and (key < arr[element_to_move_idx]):
arr[element_to_move_idx + 1] = arr[element_to_move_idx]
element_to_move_idx--
#вставляем новое значение в пустую ячейку
arr[element_to_move_idx + 1] = keyНачнём передвигать числа больше 5 вправо:

Обратите внимание: справа от передвигаемого числа возникает его копия, а оригинал перезаписывается соседом слева на следующей итерации.
А вот как выглядит массив после всех сдвиганий:

Когда цикл дойдёт до 4, он остановится и запишет число 5 вместо «мусорной» шестёрки.

Теперь взглянем на заветный код Insertion Sort:
def insertion_sort(int[] arr):
int n = arr.length
for i in 1..n:
key = arr[i]
# передвигаем в отсортированную часть элементы, которые больше, чем key
int element_to_move_idx = i – 1
while (element_to_move_idx >= 0) and (key < arr[element_to_move_idx]):
arr[element_to_move_idx + 1] = arr[element_to_move_idx]
element_to_move_idx–-
#вставляем новое значение в пустую ячейку
arr[element_to_move_idx + 1] = key
return arrПомните барьер из Selection Sort? Так как алгоритм похож, предлагаю повторить такой же трюк с Insertion Sort:
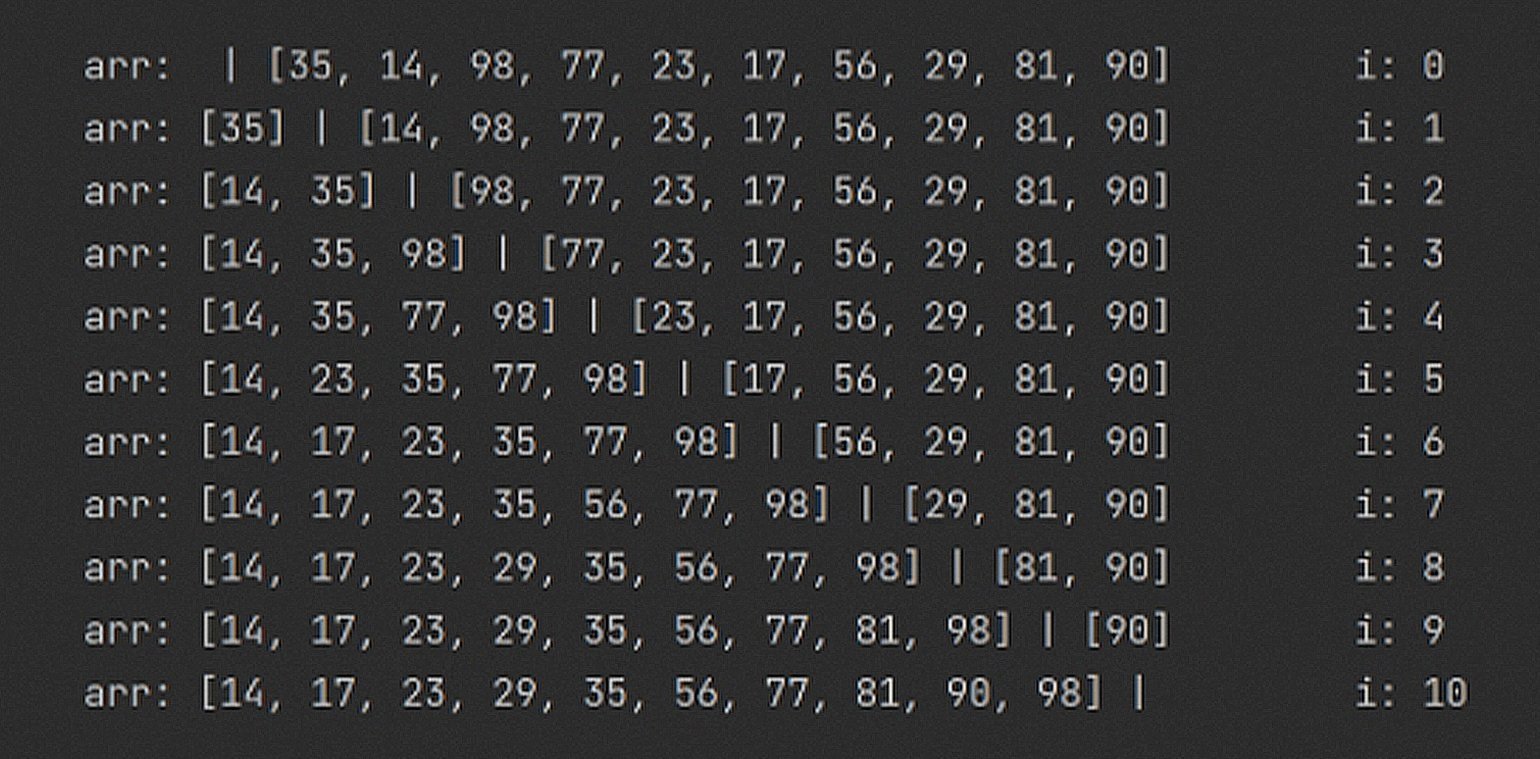
Нижняя граница производительности довольно привлекательна. Если массив изначально отсортирован, то ничего сдвигать не нужно! Сложность Best Case у такой сортировки составляет O(n).
Мы разобрали «Великую Тройку Сортировок», с которой неизбежно сталкивается любой, кто изучает алгоритмы. С чем я всех и поздравляю!
Что такое стабильность сортировки
Стабильным (устойчивым, stable) называется алгоритм сортировки, который не меняет порядок элементов с одинаковыми ключами относительно друг друга. Если мы сортируем числа, то стабильность особой роли не играет, а вот если сортируем объекты, то очень даже.
Допустим, нужно отсортировать по возрасту массив с записями о клиентах. Для наглядности возьмём максимально простой вид записей в формате [возраст : имя].

После стабильной сортировки Кузя гарантированно будет расположен выше Олега, потому что именно так расположены элементы с одинаковыми ключами в оригинальных данных.

В нестабильном варианте допускается второй сценарий:

Стабильность крайне важна, если мы планируем сортировать массив объектов по нескольким ключам. Например, сначала по возрасту, потом по размеру банковского счёта и затем по площади жилья. В таком случае нестабильный алгоритм испортит нам всю малину.
В нашей тройке стабильными являются Bubble Sort и Insertion Sort, а вот Selection Sort так и норовит перемешать элементы.
Дополним нашу таблицу характеристиками Selection Sort и строкой с показателями стабильности:
| Name | Bubble | Selection | Insertion |
|---|---|---|---|
| Name | Bubble | Selection | Insertion |
| Worst | O(n^2) | O(n^2) | O(n^2) |
| Average | O(n^2) | O(n^2) | O(n^2) |
| Best | O(n) | O(n^2) | O(n) |
| Space | O(1) | O(1) | O(1) |
| Stable | yes | no | yes |
Что не учитывает O(n)
Я обещал обсудить нюансы, которые не учитывает O-нотация. Пришло время перемывать косточки уже полюбившимся алгоритмам!
Посмотрим на почти идеально отсортированный массив. Почти — потому что самый большой элемент в нём стоит на первом месте:

Как поведут себя алгоритмы:
- Bubble Sort сработает великолепно. За n перестановок наибольший элемент «всплывёт» наверх.
- Insertion Sort тоже хорош в этом вопросе.
- Selection Sort со страшной расточительностью перелопатит весь массив и выдаст O(n^2) по времени.
Вывод: если данные почти отсортированы, то Bubble Sort и Insertion Sort — наши лучшие друзья.
Теперь подумаем о стоимости операций. В О-нотации об этом ничего не говорится, но на самом деле разные операции требуют разного количества ресурсов компьютера.
Например, прочитать значение в ячейке массива — элементарно. Перезаписать ячейку — вроде бы тоже просто, да вот только многопоточность, обновление значений в кэше процессора и другие факторы реального мира с этим не согласны. Поэтому операция swap() не так уж и проста, как кажется на первый взгляд.
А вот что у нас по количеству свопов:
- Bubble Sort просто монстр, который свопает без остановки. Количество операций записи здесь зашкаливает.
- Insertion Sort тоже не подарок — постоянное сдвигание элементов вправо до добра не доведёт.
- Selection Sort — конфетка! Всего n свопов в худшем случае. Очень экономичный алгоритм.
Вывод: если стоит задача сэкономить на операциях записи, то Selection Sort — лучший выбор.
Что касается памяти, то все три алгоритма в этом одинаково хороши. Они работают in-place и поэтому съедают O(1) памяти.
Отмечу, что алгоритмы сортировки можно улучшать. В основном с помощью особых структур данных. Например, Insertion Sort можно ускорить примерно в два раза, а также свести количество свопов к показателям Bubble Sort, если использовать не массив, а связный список. А Selection Sort можно сделать стабильным.
Что почитать и посмотреть
Код сортировок на разных языках программирования и видео с визуализацией можно найти на сайте geeksforgeeks.org:
На YouTube полно визуализаций алгоритмов сортировки, но я выделю это видео:
Отдельный мем в этой теме — венгерские танцы. Выглядит не только познавательно, но и очень забавно:)
Кажется, на этом тема простых сортировок исчерпана. Надеюсь, удалось всё разложить по полочкам и никого не запутать. В следующих статьях об алгоритмах разберу Merge Sort и Quick Sort и постараюсь залезть в материал поглубже.









