Векторное произведение векторов: что это и как посчитать
Ищем векторное произведение двух векторов и применяем правило правой руки.
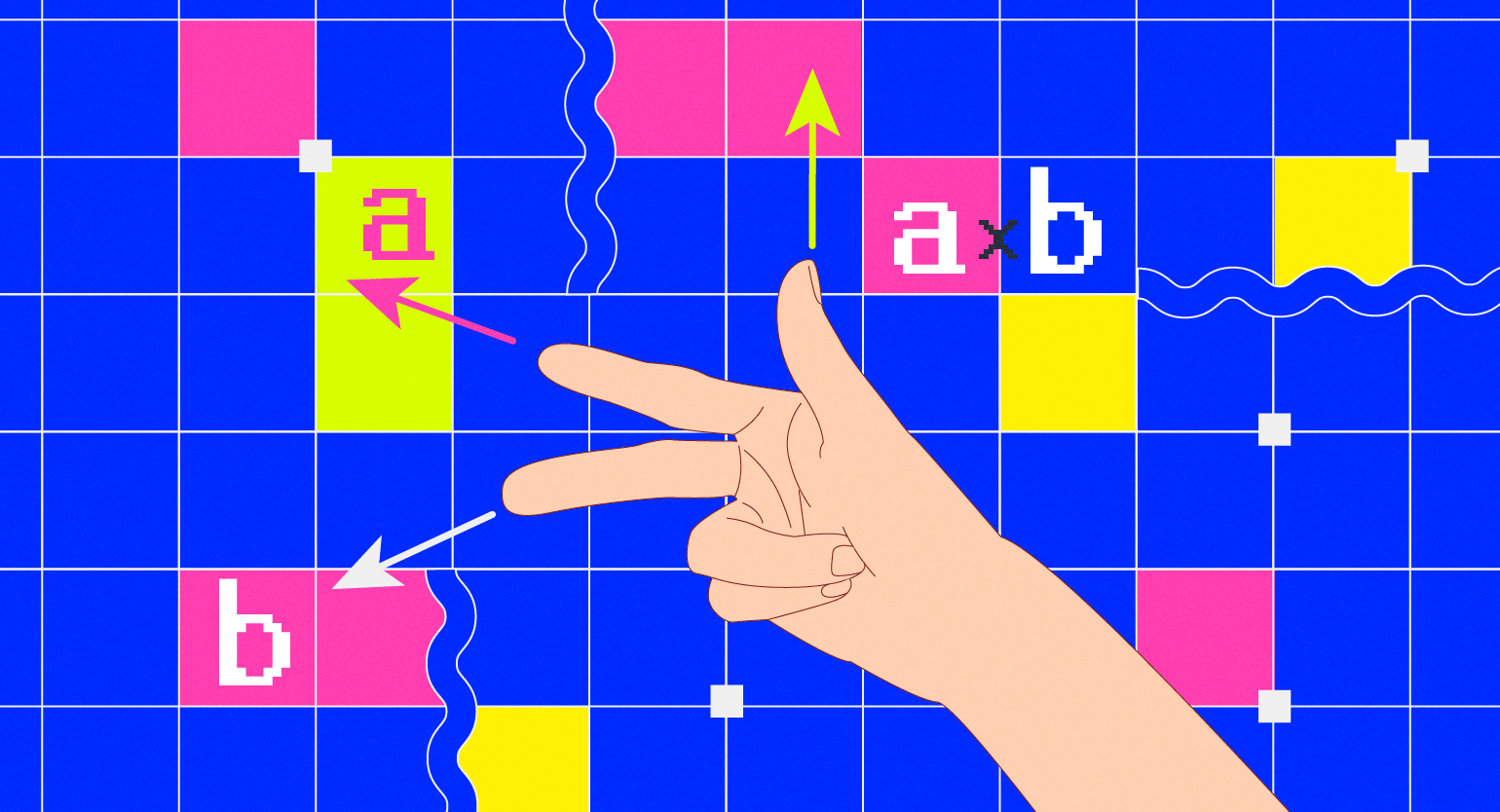

Векторное произведение векторов — это операция над двумя векторами в трёхмерном пространстве, в результате которой получается новый вектор. В мире IT эта операция нужна для выравнивания 3D-объектов, разработки физических симуляций и систем управления роботами.
В этой статье выясняем, как найти векторное произведение и какими свойствами оно обладает.
Содержание
Немного терминов
Вектор — это направленный отрезок, который соединяет две точки. У вектора есть длина и направление:
- Длина вектора — это расстояние между его началом и концом. Вектор может быть и с нулевой длиной, если его начало и конец совпадают.
- Направление показывает, куда «смотрит» вектор. Например, стрелка, нарисованная на плоскости, может указывать вверх, вниз, вправо, влево или в любую другую сторону.
Векторное произведение векторов — это операция над двумя векторами в трёхмерном пространстве, в результате которой получается новый вектор. Чаще всего операция обозначается знаком ×, например:
Если векторы коллинеарны (то есть находятся на одной прямой или параллельны), то их произведением будет нулевой вектор. Слово «нулевой» означает, что длина вектора равна нулю, а его направление невозможно определить. Такой вектор обозначают символом 

Читайте также:
Угол между векторами. Если начала векторов поместить в одну точку, как стрелки часов, то можно будет измерить угол между ними. Угол может быть от 0° до 180°. Если угол меньше 90°, то векторы считаются направленными в одну сторону. Если угол равен 90°, то векторы перпендикулярны друг другу. Если угол больше 90°, то векторы направлены в противоположные стороны. Когда угол равен 0° или 180°, векторы называются коллинеарными.
Свойства результирующего вектора
Как мы отметили ранее, векторное произведение образует новый вектор — в математике он называется результирующим. У него есть следующие свойства:
1. Новый вектор перпендикулярен паре исходных векторов. Например, векторное произведение может выглядеть так:
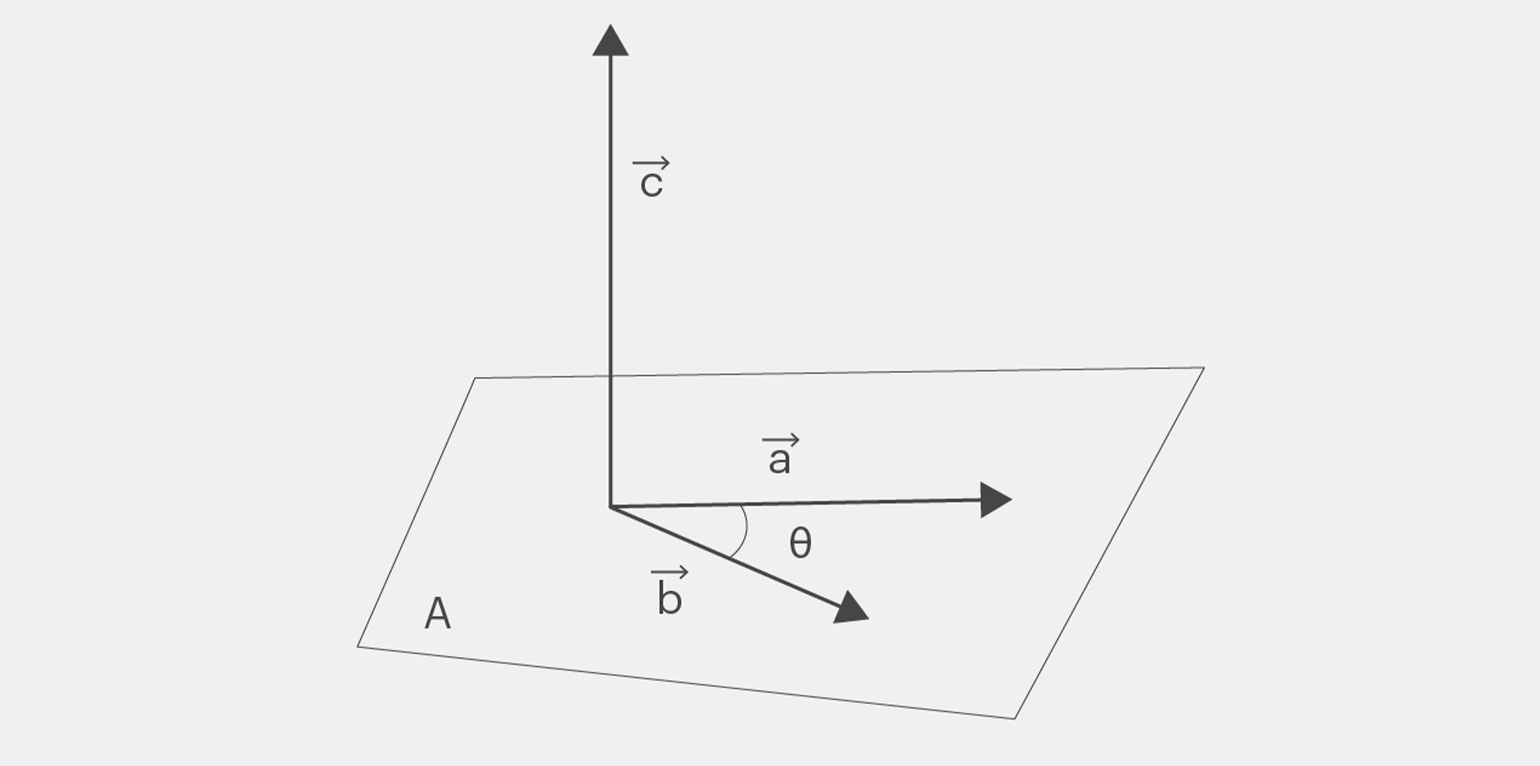
Инфографика: Майя Мальгина для Skillbox Media
На рисунке выше 



2. Длина нового вектора равна произведению длин исходных векторов и синуса угла между ними. Формула для модуля векторного произведения векторов 

В этой формуле 




3. Вектор 






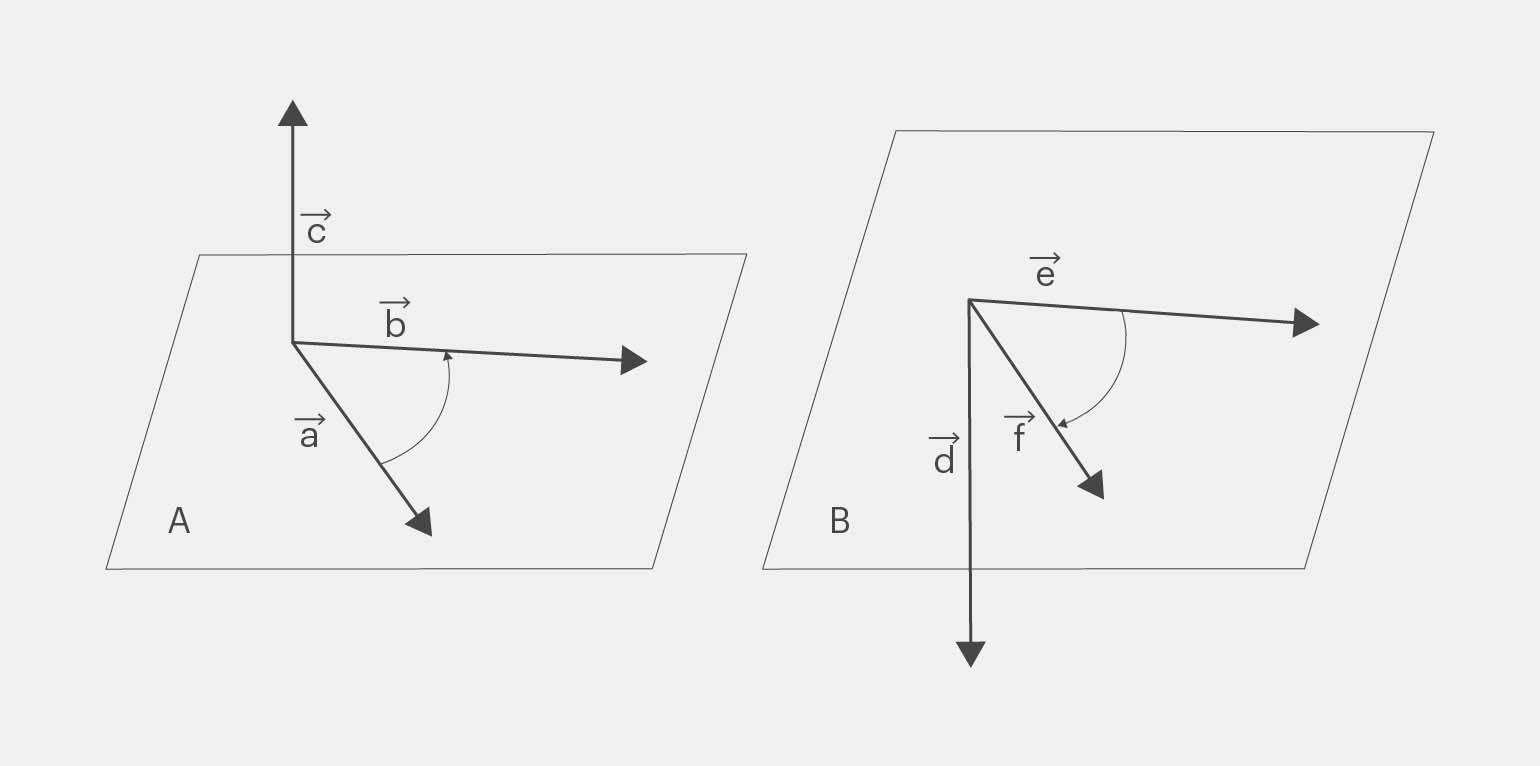
На рисунке слева видно, что если смотреть с конца вектора 




На рисунке справа вращение вектора 








Правило правой руки
Направление вектора, полученного в результате векторного произведения, можно определить по правилу правой руки. Самый простой его вариант звучит так: если разместить указательный палец правой руки на первом векторе, а средний на втором, то отогнутый перпендикулярно к ладони большой палец покажет примерное направление произведения векторов.
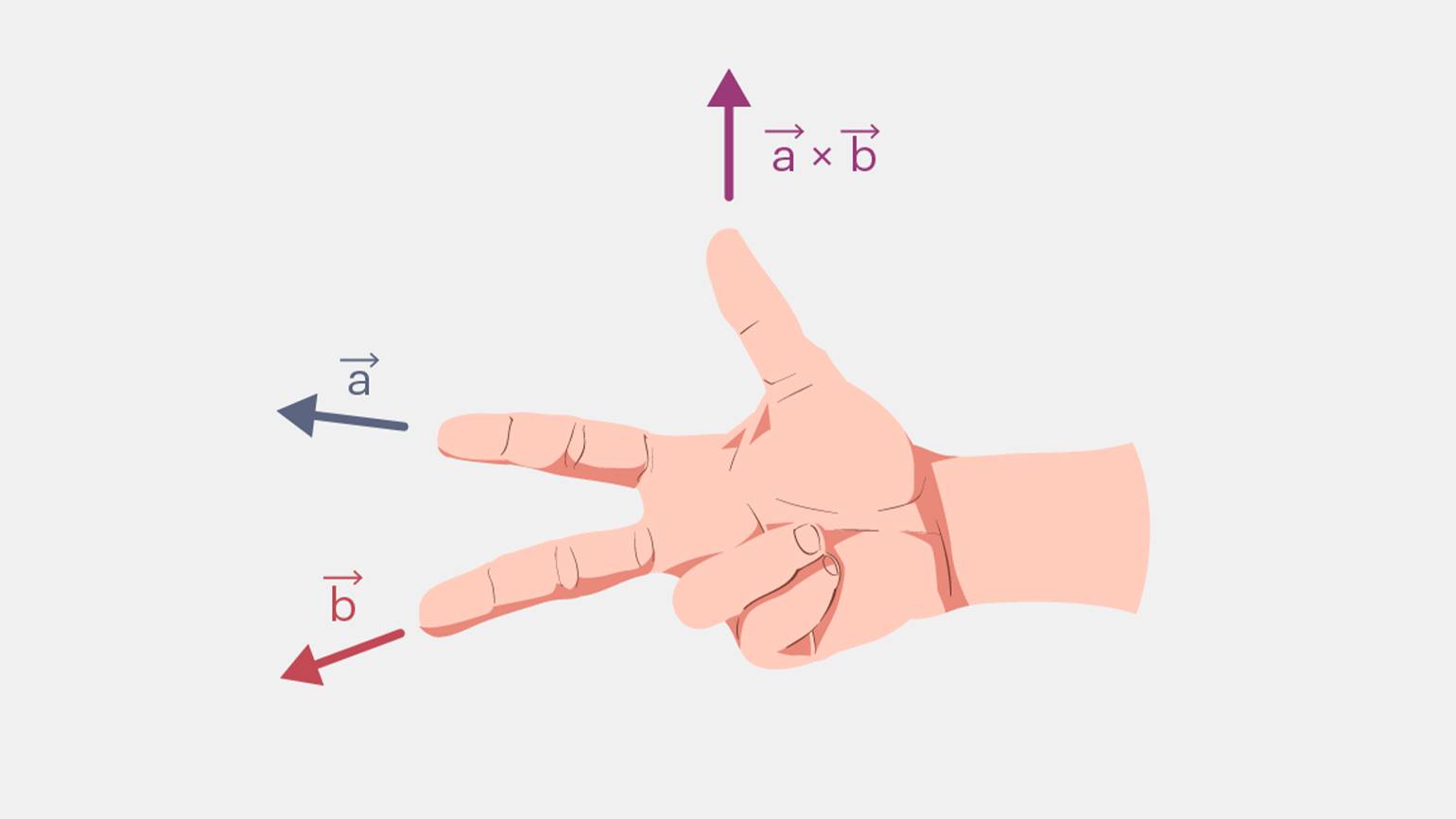
 и
и 
Инфографика: Майя Мальгина для Skillbox Media
Свойства векторного произведения
Векторное произведение векторов обладает несколькими важными свойствами.
Антикоммутативность
Антикоммутативность — свойство математических операций, при котором, если изменить порядок операндов, результат изменится на противоположный. Обратное для этого свойство — коммутативность, когда порядок операндов не влияет на результат. Например, при сложении и умножении: 10 + 5 = 5 + 10 = 15.
Векторное произведение векторов — антикоммутативная операция, которая зависит от порядка векторов. Если поменять векторы местами, то результат изменит знак:
Дистрибутивность относительно сложения
Дистрибутивность относительно сложения — математическое свойство, которое означает, что выражение, умноженное на сумму, можно сначала умножить на каждое слагаемое, а после сложить. Результат при этом не изменится. Например:
2 × (3 + 4) = 2 × 7 = 14
2 × 3 + 2 × 4 = 6 + 8 = 14
Векторное произведение векторов также дистрибутивно относительно сложения:
Читайте также:
Ассоциативность умножения на скаляр
Ассоциативность умножения на скаляр — математическое свойство, которое означает, что при умножении нескольких чисел или векторов на скаляр (обычное число) не важен порядок выполнения операции. Например:
Координаты векторного произведения
Векторное произведение двух векторов в трёхмерном пространстве можно выразить через их координаты на осях X, Y, Z.
Пусть даны два вектора 

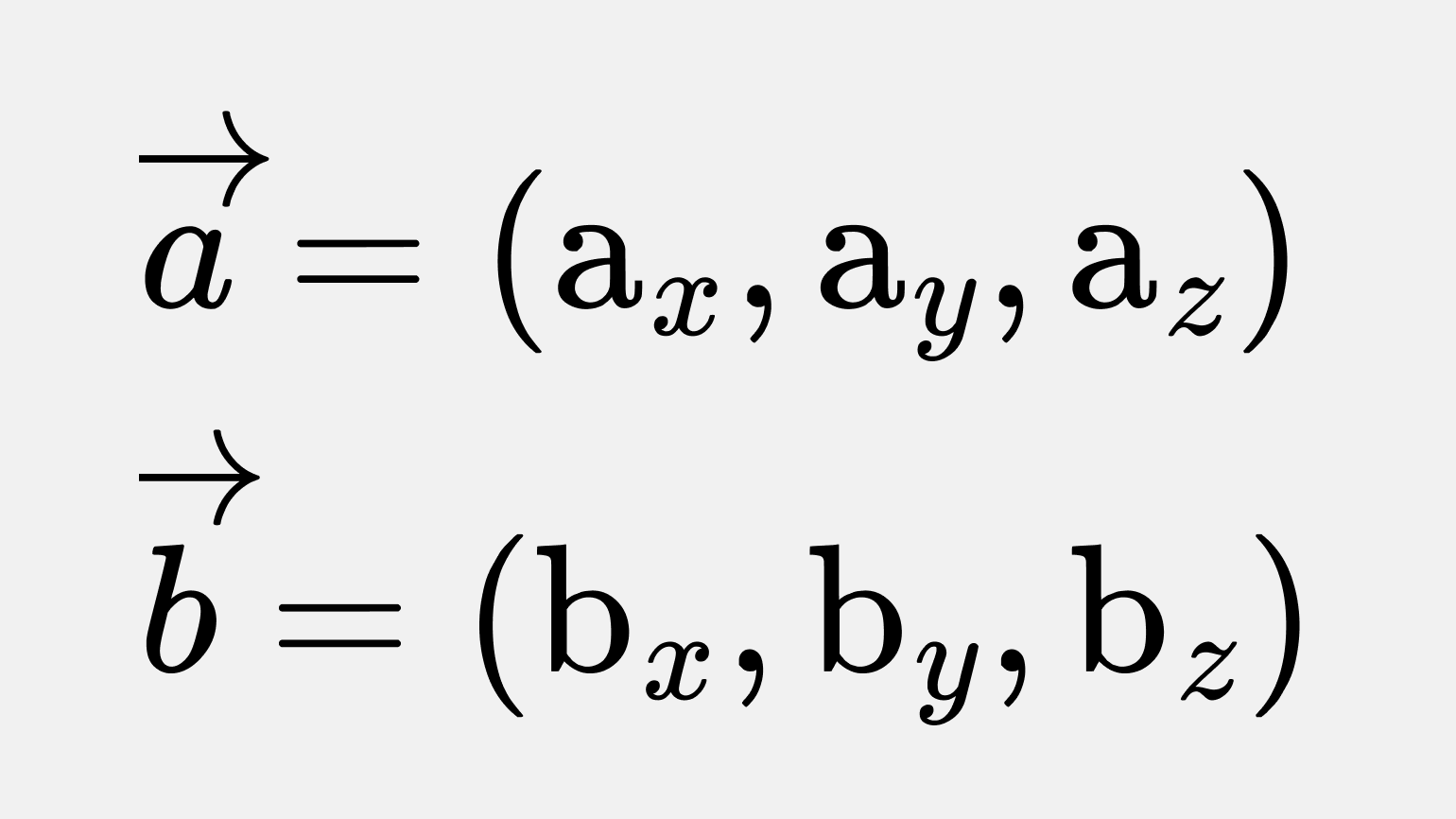
Тогда их векторное произведение 






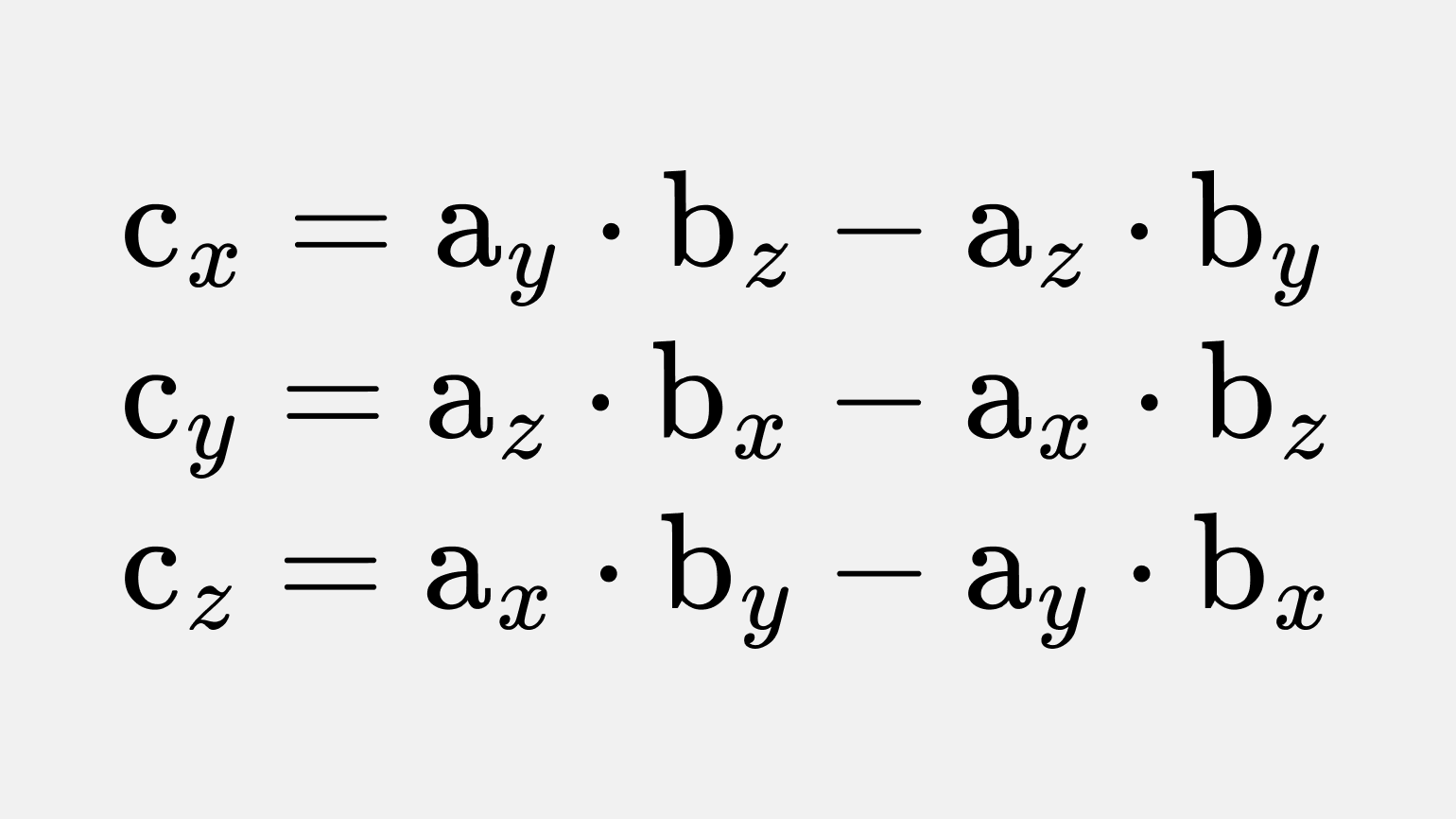
Эти формулы можно получить из определения векторного произведения через определитель матрицы. Если записать векторное произведение в виде матрицы, это будет выглядеть так:
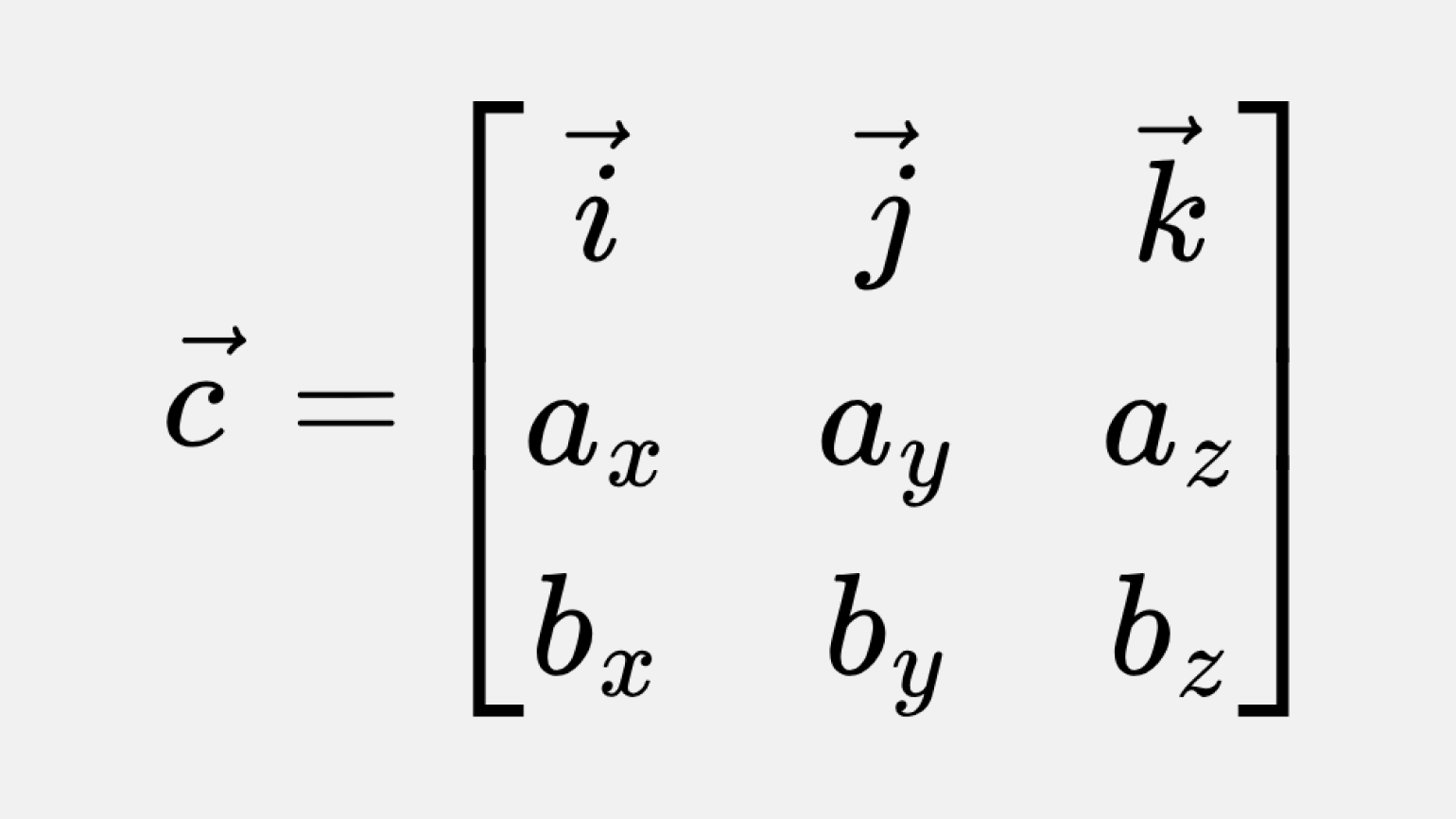
В формуле выше 


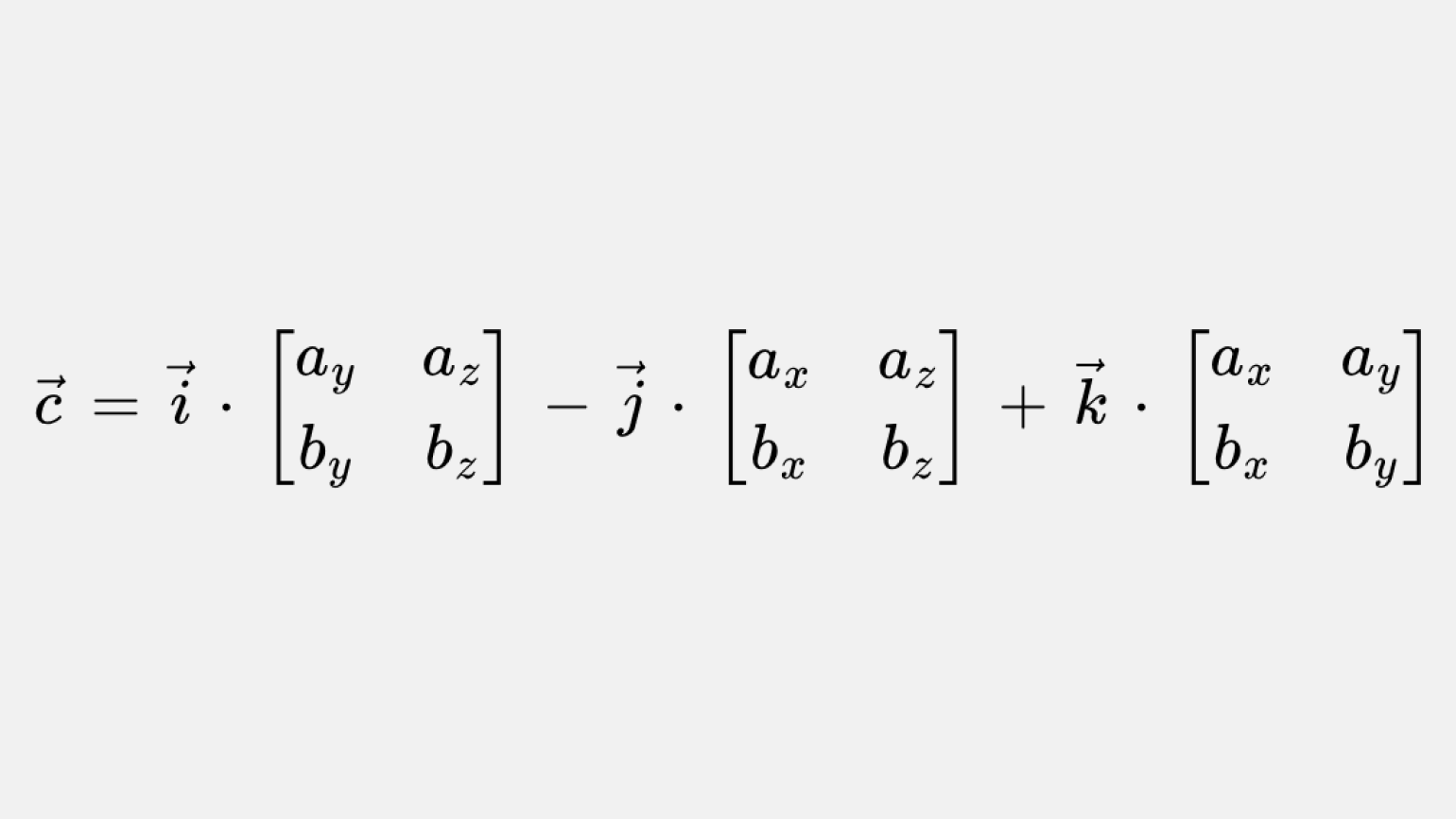
Продолжим вычисление определителя:
Таким образом, координаты векторного произведения двух векторов 


Геометрический смысл векторного произведения
Векторное произведение векторов встречается не только в алгебре, но и в геометрии. Например, с помощью этой операции можно найти площадь параллелограмма.
Если у вас есть векторы 

При этом длина векторного произведения определяется по той же формуле. Это значит, что модуль длины векторного произведения численно равен площади параллелограмма, построенного на исходных векторах.
Физический смысл векторного произведения
С помощью векторного произведения можно описать физические явления, в которых важно учитывать направления и величину результирующих векторов. Например, произведение позволяет выразить момент силы, линейную скорость точки вращающегося тела и силу Лоренца.
Момент силы
В физике момент силы относительно точки или оси определяется как векторное произведение радиус-вектора, проведённого от этой точки до точки приложения силы, и самой силы.
Формула момента силы 
В ней 

Момент силы показывает, насколько эффективно сила вызывает вращение вокруг данной точки или оси. Его направление указывает на ось вращения, а величина — на интенсивность этого вращения.
Линейная скорость точки на вращающемся теле
Вращение тела вокруг оси описывается вектором угловой скорости 

Где 
В этом случае направление линейной скорости перпендикулярно как к вектору угловой скорости, так и к радиус-вектору.
Сила Лоренца
В электромагнитных явлениях сила Лоренца, действующая на заряд, движущийся в магнитном поле, также определяется через векторное произведение:
В этом случае q — заряд, 

Сила Лоренца перпендикулярна как направлению движения заряда, так и направлению магнитного поля, что приводит к закручиванию траектории заряженной частицы.
Что запомнить
- Векторное произведение векторов — это операция над двумя векторами в трёхмерном пространстве, в результате которой получается третий вектор.
- Произведение обычно записывают так:
- Направление результирующего вектора можно найти с помощью правила правой руки: если разместить указательный палец правой руки на первом векторе, а средний на втором, то большой палец покажет направление результирующего вектора.
- Векторное произведение обладает следующими свойствами:
- Антикоммутативность:
- Дистрибутивность относительно сложения:
- Ассоциативность умножения на скаляр:
- Длина векторного произведения равна площади параллелограмма, построенного на этих векторах:
, где
и
— векторы,
и
— их модули, а
— угол между ними.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!