Теория графов: деревья, планарность, разновидности графов
Разбираемся с графом, но не Монте-Кристо.


Если вы начинали изучать алгоритмы (например, алгоритм Дейкстры), то наверняка сталкивались с понятием «граф». И нет, речь вовсе не про изнеженных дворян, которые предавались неге в своих поместьях и продавали крестьян за бесценок :) В математике графы — это важнейшая структура для моделирования связей между объектами. С их помощью строят оптимальные маршруты, составляют карты социальных связей и проектируют сложные системы. Рассказываем, что такое графы и какие они бывают, а также показываем на примерах, чем они полезны.
Содержание

Эксперт
Пётр Емельянов
Эксперт Skillbox, CEO в Bloomtech, специалист по информационной безопасности и анализу данных. Опыт в IT — 20 лет.
Что такое граф
Граф — это математическая структура, которая используется для моделирования связей между различными объектами. Граф состоит из вершин и рёбер, которые их соединяют.
Проще всего понять природу графов на примере. Представьте, что у нас есть три города с незамысловатыми названиями A, B, C, которые соединены дорогами AB, AC и BC. На рисунке это можно изобразить так:
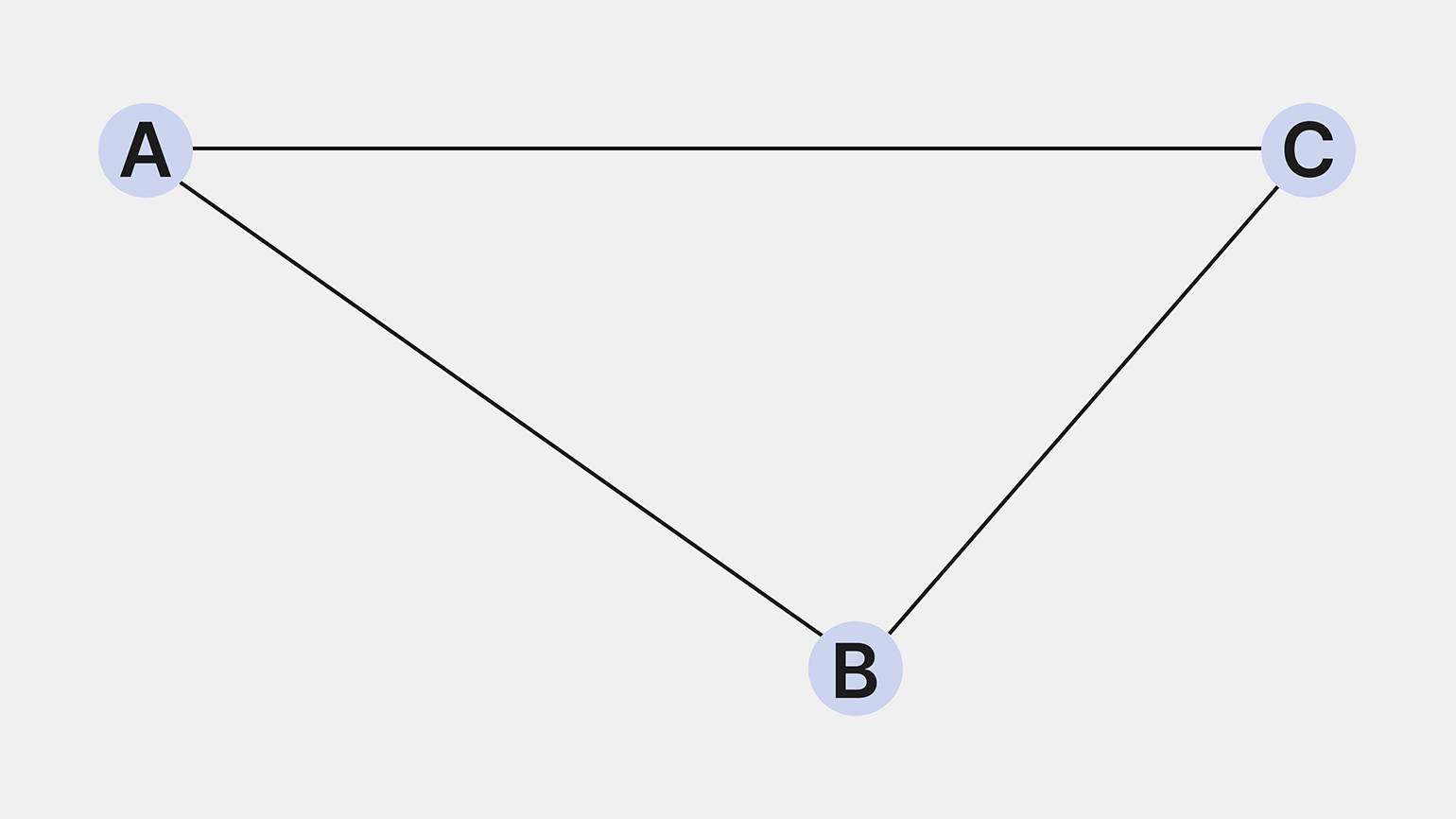
Изображение: Skillbox Media
Рисунок, который у нас получился, и есть граф. Он состоит из следующих элементов:
- Вершины. Ключевые точки или объекты в графе. Это могут быть, например, города на карте, веб-страницы в интернете или отделы в компании.
- Рёбра. Линии, которые соединяют вершины. Например, дорога между двумя городами, гиперссылка между веб-страницами или взаимодействие между отделами в компании.
С помощью графов хорошо получается изображать сложные связи, для которых не подходят другие способы визуализации. Например, с помощью графа можно показать карту социальных связей человека, в которой вершинами будут люди, а рёбрами — взаимоотношения.
Основные понятия теории графов
В графах рёбра и вершины могут иметь разные виды связей друг с другом. Это позволяет строить гибкие связи между объектами и отражать больше полезной информации на рисунке.
Ребро, соединяющее одну вершину с другой, называется инцидентным этим вершинам. Например, ребро AB соединяет вершины A и B. Оно будет инцидентно как вершине A, так и вершине B. Отношение инцидентности существует только между вершиной и ребром, два ребра или две вершины не могут быть инцидентными.
Рёбра могут быть направленными и ненаправленными. Если вершины A и B соединяет ребро и из A можно попасть в B и обратно, то ребро будет ненаправленным. Например, дорога, соединяющая города A и B, по которой можно попасть как из A и B, так и из B в A, — это ненаправленное ребро между вершинами графа A и B.
Если же из A можно попасть в B, но из B в A нельзя, то ребро будет направленным из A в B. Ненаправленные рёбра могут показывать не только дороги между городами, но и подписки в социальных сетях. Например, если пользователь подписался на друга, но тот не ответил взаимностью, то такую связь называют ненаправленной.
Если все рёбра в графе имеют направление, такой граф называется направленным (или ориентированным), если все рёбра без направления, то граф называется ненаправленным (неориентированным), и, наконец, если в графе некоторые рёбра направленные, а некоторые нет, граф именуется смешанным.
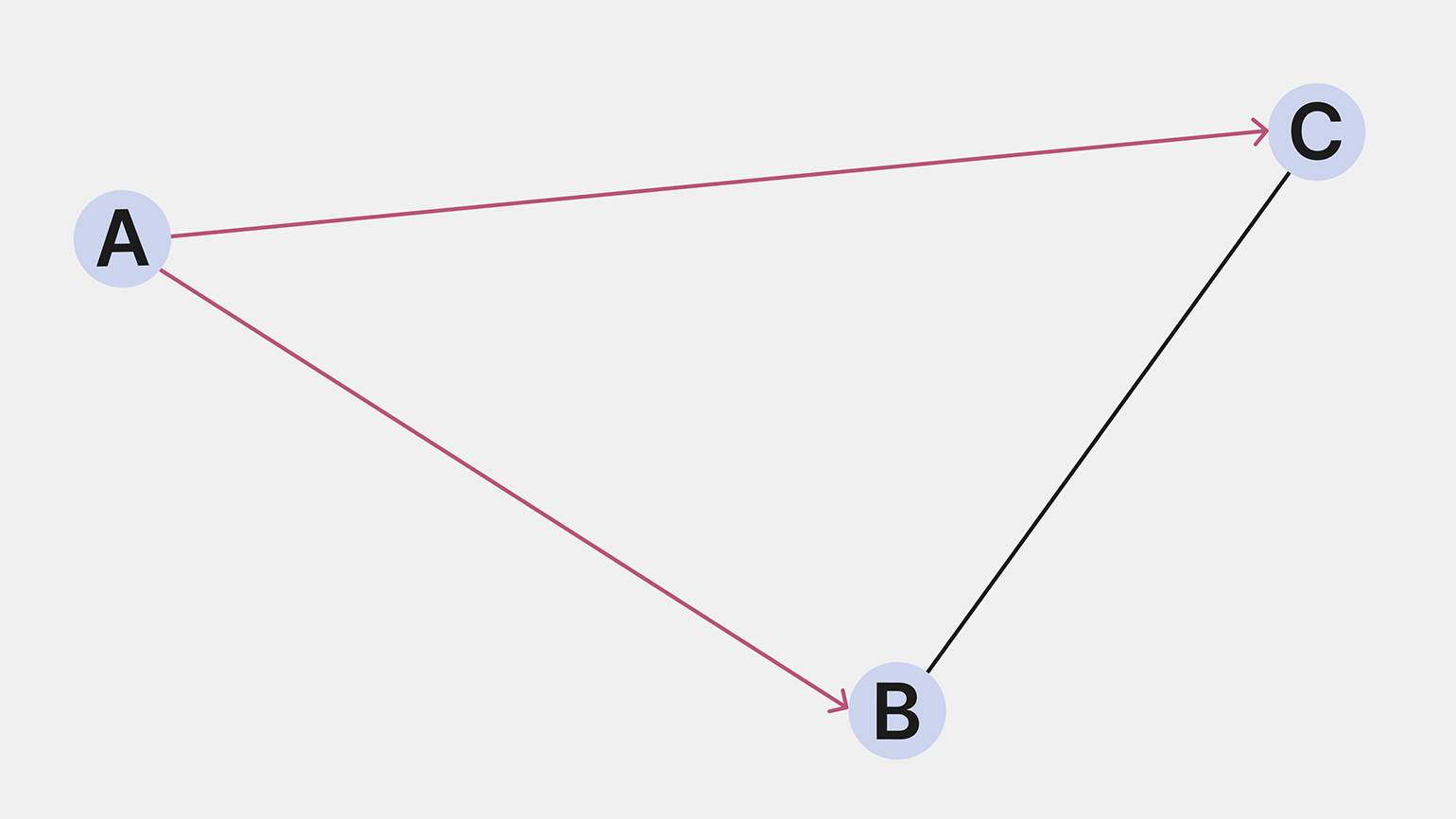
Изображение: Skillbox Media
Петля (или цикл) — особый вид ребра, которое начинается и заканчивается в одной и той же вершине. В социальной сети петля может означать, например, что человек отправил сообщение сам себе. Если в графе нет ни одной петли (цикла), такой граф называется ациклическим.

Изображение: Skillbox Media
Свойства есть и у вершин графа:
- Если две вершины соединены ребром, то их называют смежными.
- Вершина без инцидентных рёбер — изолированная вершина.
- Если у вершины есть только одна связь с другими объектами в графе, то её называют висячей.
- Степень вершины — количество рёбер, которые выходят из неё.
Изображение: Skillbox Media
Путь, цепь и цикл в графе
В теории графов путь, цепь и цикл — способы перемещения от одной вершины к другой. Эти понятия помогают решать задачи, которые возникают при поиске оптимальных маршрутов или при моделировании сложных систем связей.
Разновидности маршрутов в графах:
- Путь — конечная или бесконечная последовательность вершин и рёбер, в которой конец одного ребра является началом следующего.
- Цепь — это последовательность рёбер, в которой каждое ребро связано со следующим с помощью общей вершины. В цепи могут повторяться вершины, но не рёбра.
- Цикл — особый случай пути, который начинается и заканчивается в одной и той же вершине. При этом все рёбра и вершины (кроме начальной и конечной) уникальны. Важное условие цикла: вы не должны проходить по одному и тому же ребру дважды.
Виды графов
Существует множество видов графов, каждый из которых полезен для отображения определённых типов связи между объектами.
Ориентированные, неориентированные и смешанные графы
- Ориентированный. Граф, в котором каждое ребро указывает своё направление с помощью стрелок, по которым можно передвигаться. Например, когда есть путь A → B → C, но нет обратных рёбер; вернуться из C в A нельзя.
- Неориентированный. Граф, в котором рёбра не указывают направление. Это значит, что из любой вершины можно попасть в любую точку графа.
- Смешанный. Граф, который содержит как ориентированные, так и неориентированные рёбра.
Графы с петлями и мультиграфы
- Граф с петлями. Рёбра графа, которые начинаются и заканчиваются в одной и той же вершине, называются петлями. Например, если мы строим схему связей в социальной сети, то с помощью петли можно показать, что пользователь ставит лайки своим же публикациям.
- Мультиграф. Если между двумя графами существует несколько рёбер, то такой граф будет называться мультиграфом. Такие графы часто используются в схемах транспортных систем, когда между городами есть несколько разных маршрутов (железная дорога, автомобильная дорога и авиарейсы).
Пустые и полные графы
Пустой граф. Тип графа, который не содержит рёбер. У него могут быть вершины, но между этими вершинами нет никаких связей. Так можно показать системы, в которых есть объекты, не взаимодействующие с другими объектами. Например, в схеме социальных связей так можно изобразить человека, который ни с кем не общается.
Полный граф. Граф, в котором каждая вершина соединена ребром с каждой другой вершиной. Так можно показать коллектив, в котором все знают друг друга.
Связный граф
Связный граф — граф, в котором существует путь между любой парой вершин. Из каждой вершины по рёбрам можно добраться до любой другой вершины. В связном графе нет изолированных вершин или групп, которые не связаны с остальными частями графа.
Взвешенный граф
Взвешенный граф — граф, в котором каждому ребру присвоено числовое значение — вес. Это может быть расстояние, время, стоимость, мощность или другая характеристика, связанная с соединением вершин.
Допустим, между двумя городами проложены две дороги: гладкое асфальтированное шоссе и грунтовка. Понятно, что на машине гораздо приятнее (и дешевле) ехать по асфальту, поэтому вес ребра, моделирующего шоссе, будет ниже.
Двудольный граф
Двудольный граф — граф, в котором вершины можно разделить на две группы так, что рёбра будут соединять только вершины из разных групп. То есть внутри одной группы вершины не соединены рёбрами.
Представим, что у нас есть группа студентов и группа курсов. Студенты записываются на курсы. Отобразим эту ситуацию с помощью графа:
- Вершины из первой группы (A, B, C) — это студенты.
- Вершины из второй группы (K, M) — это курсы.
- Рёбра — запись студентов на курсы.
В графе ниже студент A записан на курс K, B на M, а С на оба курса. Выходит, что вершины из множества студентов соединены с вершинами из множества курсов, но не соединены между собой:
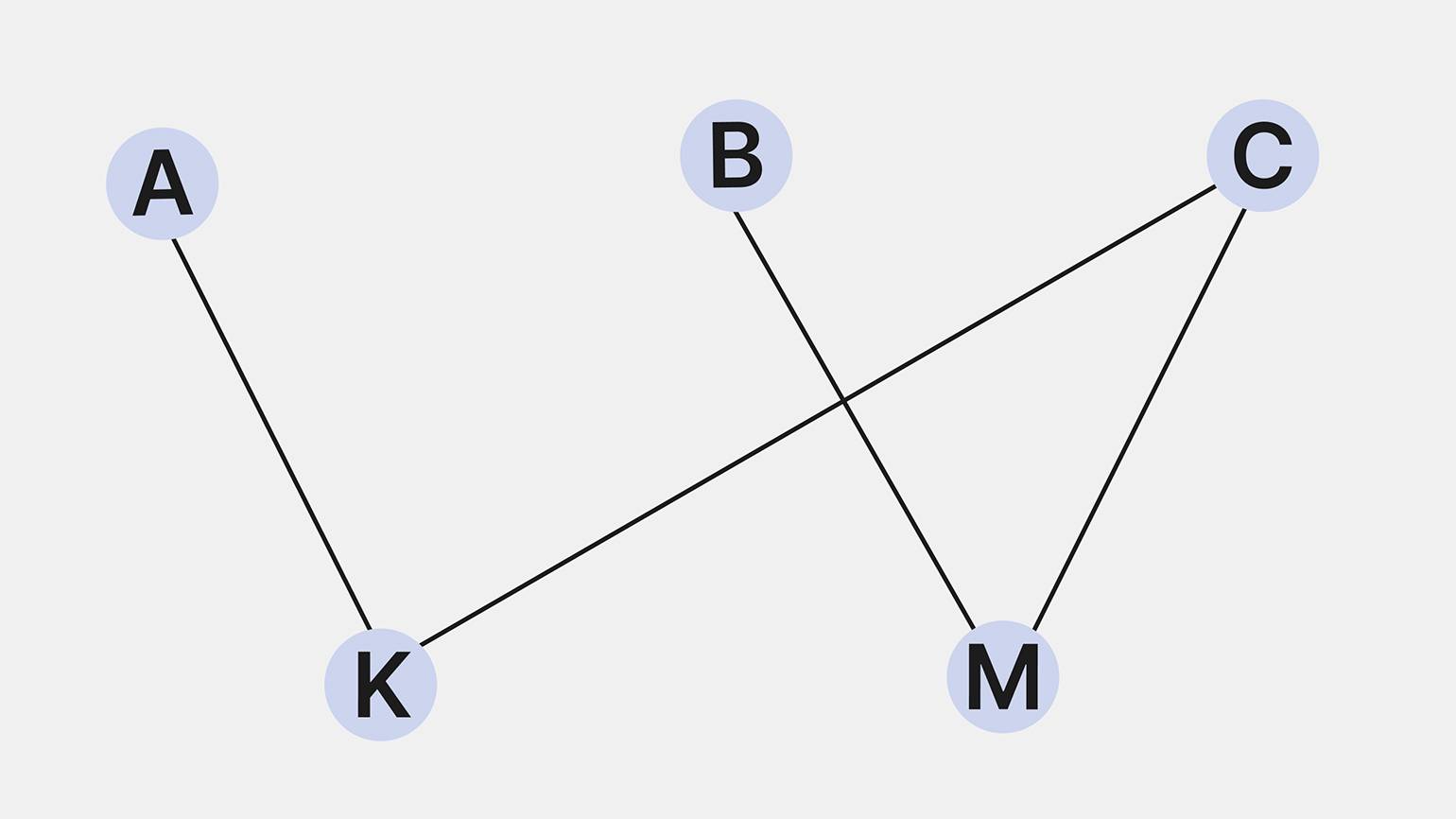
Планарный граф
Планарный граф — граф, который можно нарисовать на плоскости так, чтобы его рёбра пересекались только в вершинах, но не между собой.
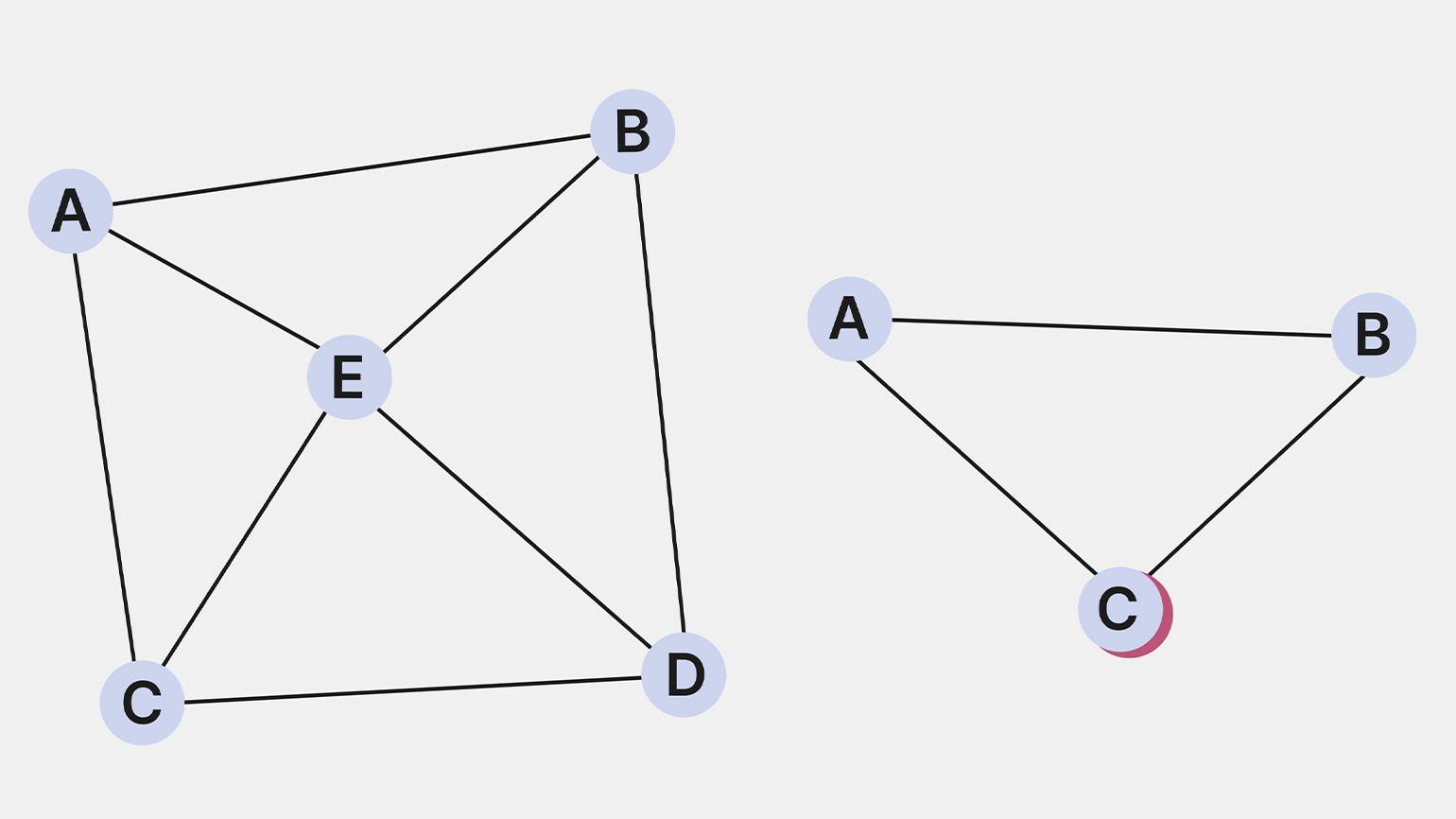
Изображение: Skillbox Media
Эйлеров граф
Эйлеров граф — граф, в котором существует цикл, который проходит по каждому ребру ровно один раз и возвращается в исходную вершину. Также существует полуэйлеров граф — когда цикл проходит по всем рёбрам ровно один раз, но не возвращается в исходную вершину.
Эйлеровы графы используются для решения задач, связанных с поиском оптимального пути. Например, при прокладке туристических маршрутов или при планировании логистических цепочек.
Вы могли слышать про старинную математическую задачу о кёнигсбергских мостах: в городе Кёнигсберге (сегодня Калининград) через реку Прегель (сегодня Преголя) построено семь мостов. Можно ли прогуляться по всем мостам, не заходя на один мост дважды? Эту задачу в 1736 году решил математик Леонард Эйлер, впервые в истории применив теорию графов. А циклические графы, которые он изобрёл в процессе решения, впоследствии назвали эйлеровыми в его честь.
Ответ, кстати, в том, что прогуляться по мостам таким образом невозможно. Если не верите, приезжайте в Калининград и попробуйте сами :)
Деревья в графах
Существует особый вид графов, в которых нет замкнутых областей, но между каждой парой вершин проложен путь. Такие графы называются деревьями и широко используются в алгоритмах поиска и сортировки данных.
Основные свойства деревьев:
- Между любыми двумя вершинами существует связь.
- Между любыми двумя вершинами есть единственный путь. Это означает, что не может быть двух разных путей, соединяющих одну и ту же пару вершин.
- В дереве с n вершин ровно n − 1 рёбер. Это фундаментальное свойство деревьев.
Есть разные виды деревьев, предназначенные для решения различных задач:
- Корневое дерево. Это дерево, в котором одна вершина выделена как корень. В таком дереве определено направление вниз от корня к «листьям» (вершинам, не имеющим потомков). Вершины графа делятся на родительские и дочерние. Например, если вершина A родительская для B и C, то B и C — дочерние для A.
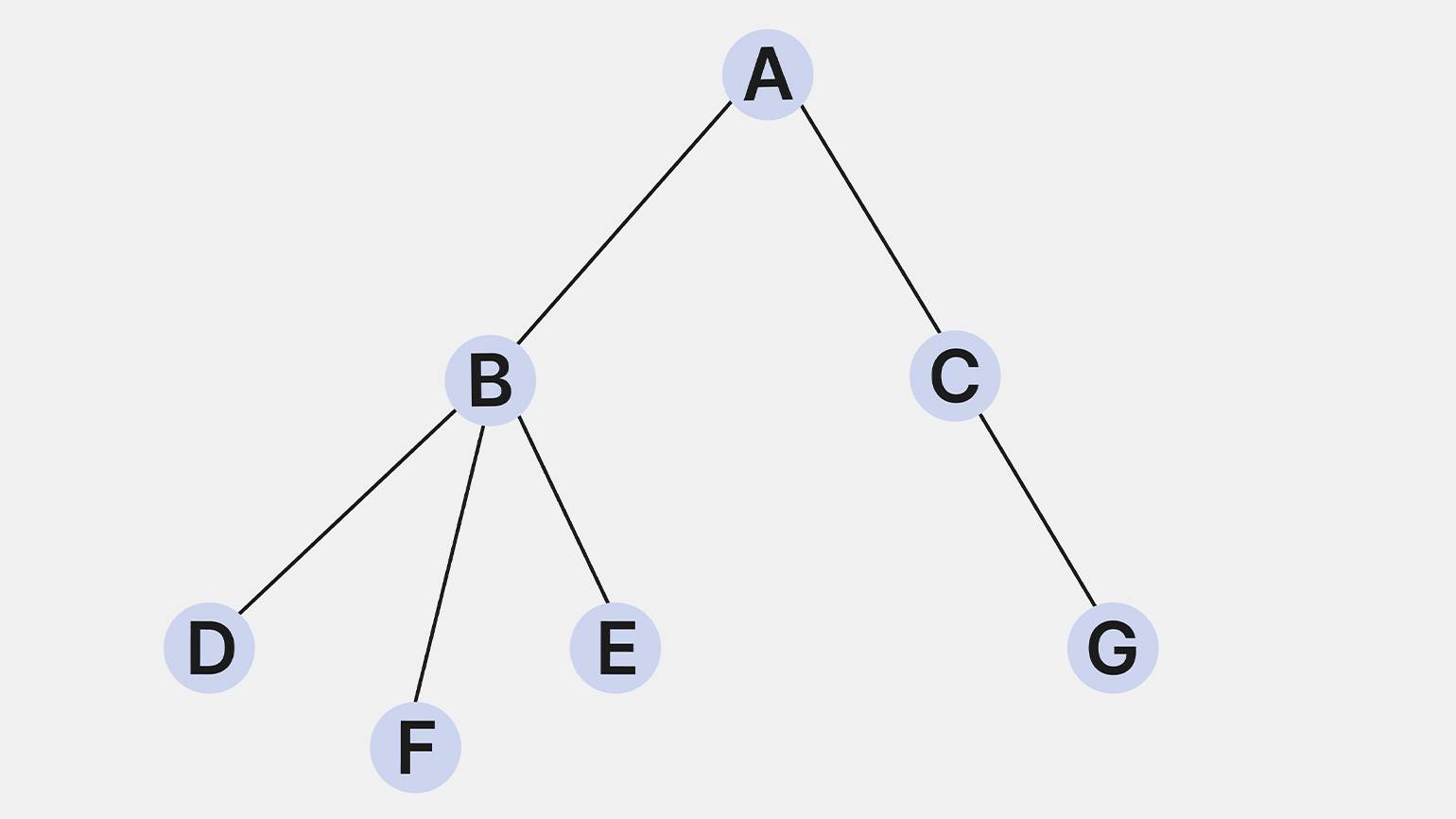
Изображение: Skillbox Media
Например, структура файлов в компьютере организована как корневое дерево, в котором есть родительская директория и дочерние файлы.
- Бинарное дерево. Это дерево, в котором каждая вершина имеет не более двух потомков. Бинарные деревья часто используются для организации поиска информации.
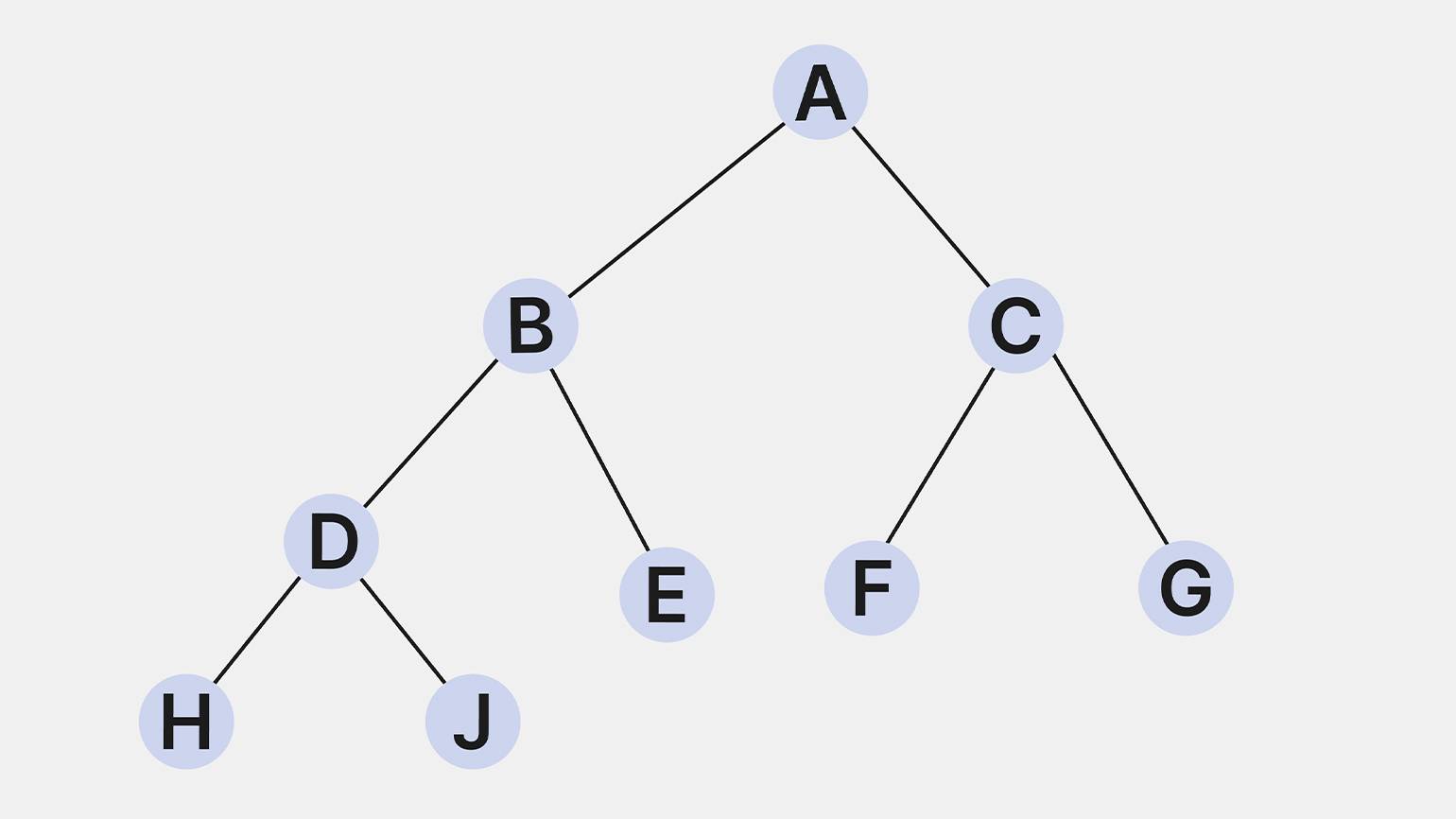
Изображение: Skillbox Media
- Бинарное дерево поиска (BST). Бинарное дерево, в котором для каждого узла выполняется условие: значения всех узлов в левом поддереве меньше значения родительского узла, а в правом поддереве — больше или равны ему. BST обеспечивает эффективный поиск, вставку и удаление элементов.
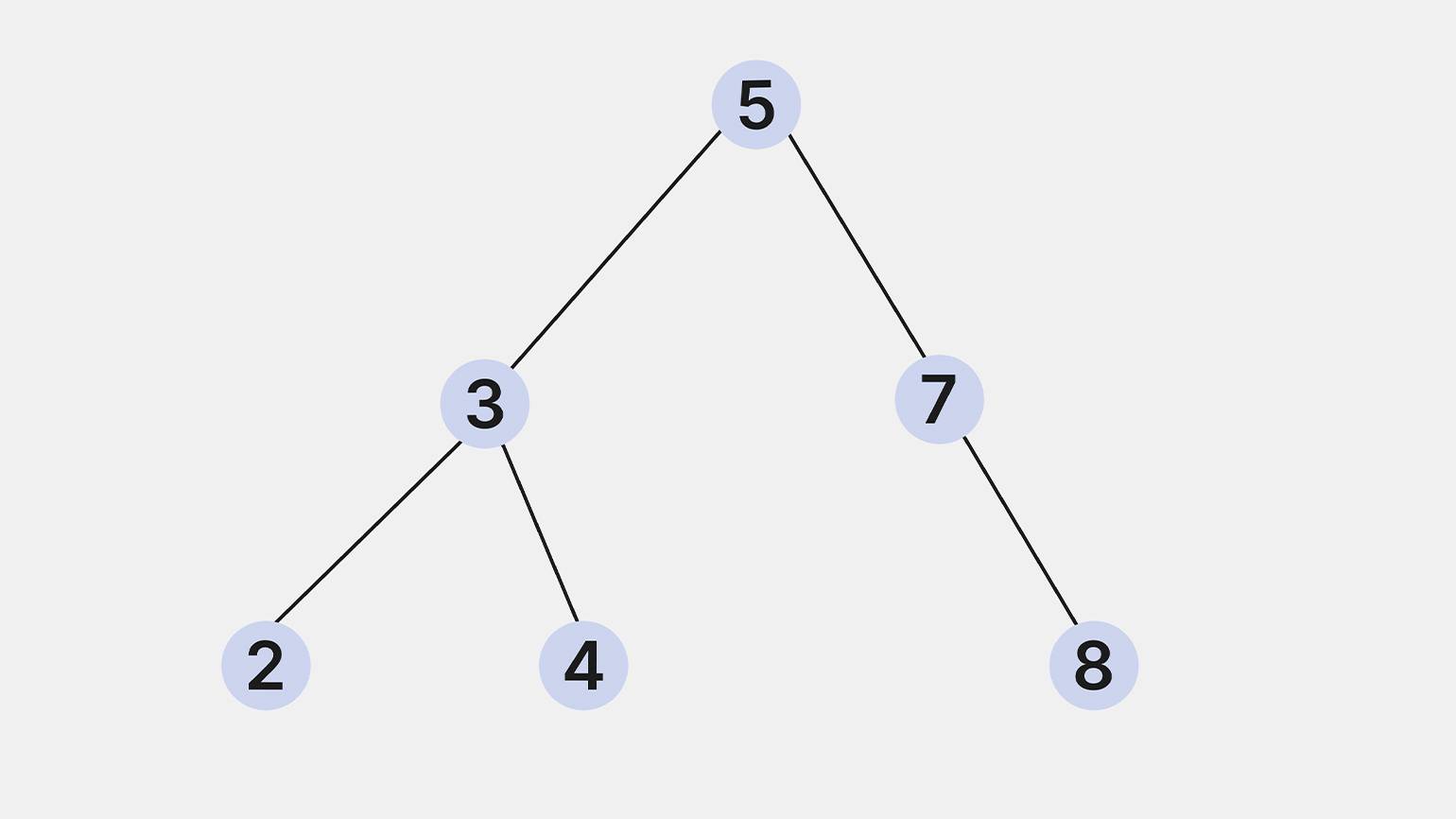
Изображение: Skillbox Media
Что запомнить
- Граф — это математическая структура, с помощью которой можно отображать различные объекты и взаимоотношения между ними. Графы состоят из вершин и связывающих их рёбер.
- У некоторых графов, например эйлеровых или деревьев, есть уникальные свойства, подходящие для решения специфичных задач.
- С помощью графов можно искать оптимальные маршруты, составлять карты социальных связей, строить схемы оборудования в локальной сети и организовывать поиск информации.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!





