Алгоритм Дейкстры: что это такое, как работает и где используется

Все мы пользуемся приложениями-навигаторами — вводим начальную и конечную точки, а программа строит самый оптимальный, на её взгляд, маршрут. Для этого она использует так называемые алгоритмы поиска кратчайшего пути. Сегодня поговорим о самых популярных из них — алгоритмах Дейкстры и А*. Выясним, как они работают, где применяются и чем отличаются друг от друга.

Самое начало: теория графов

Алгоритм Дейкстры — это метод нахождения кратчайших путей от одной вершины графа ко всем остальным.

Граф — это математическая структура, которая состоит из вершин (узлов) и рёбер (связей) между ними. Рёбра могут иметь направление, а также веса — числа, которые обозначают силу связей с вершинами.

Графы используются для представления объектов, их взаимосвязей и отношений между ними. Например, в виде графа можно представить социальную сеть, где вершины — это пользователи, дружеские связи между ними — рёбра, а веса — это, скажем, частота обмена сообщениями.

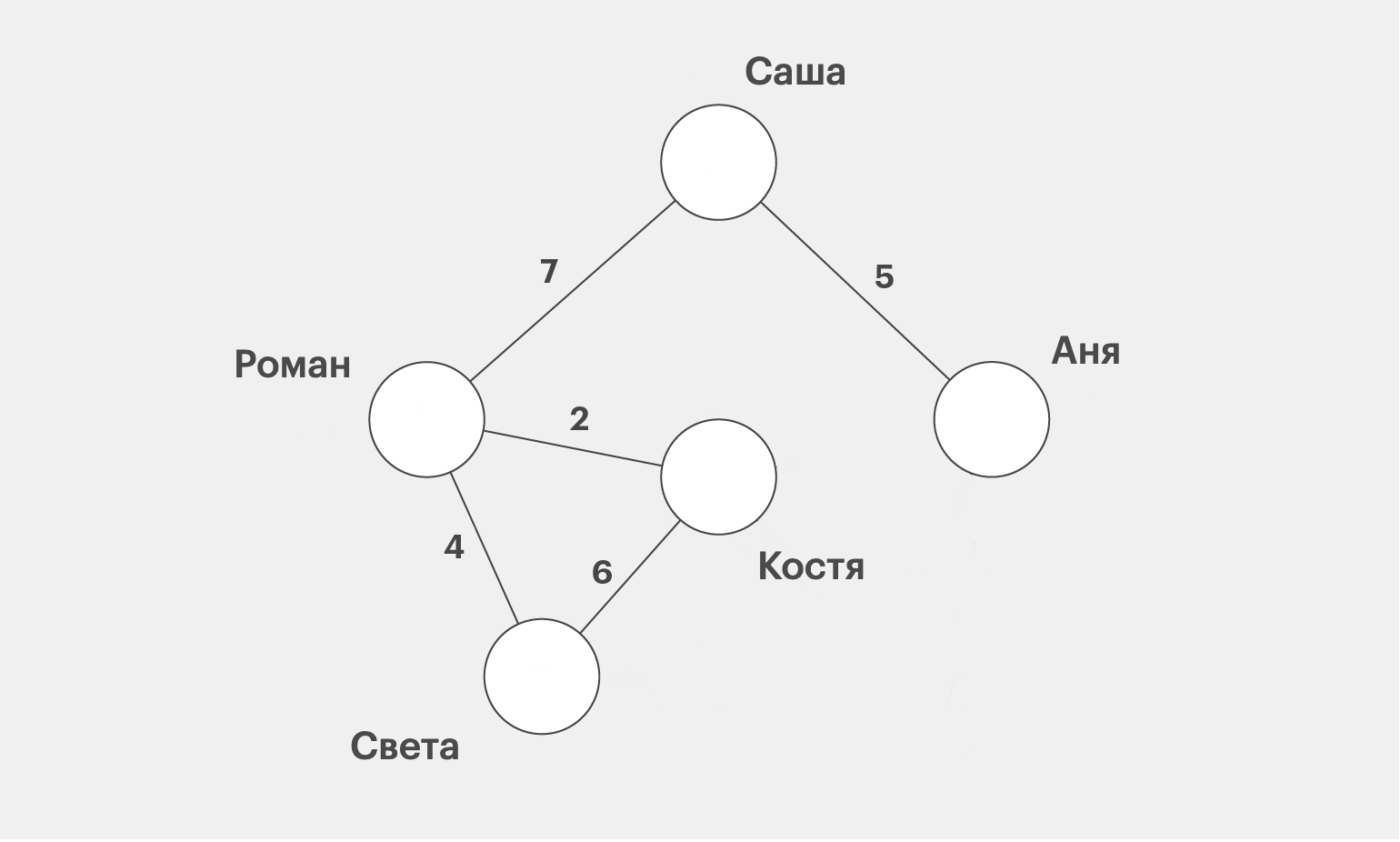
Но, конечно, одними социальными сетями прикладной смысл графов не ограничивается. Например, с их помощью можно моделировать связи между:

• веб-страницами;
• улицами и перекрёстками при проектировании дорожной сети;
• генами, белками и молекулами в биоинформатике;
• пунктами доставки грузов в логистике;
• точками передвижения роботов в робототехнике.

Как работает алгоритм Дейкстры

Идея алгоритма Дейкстры в том, что мы можем найти наименьшие расстояния от начальной вершины графа ко всем остальным. Зная эти расстояния, можно построить кратчайший маршрут между начальной и другими точками.

Допустим, у нас есть несколько городов, соединённых дорогами. Назовём их А, B, C, D, E, F. Числа возле рёбер — расстояния между городами в милях.

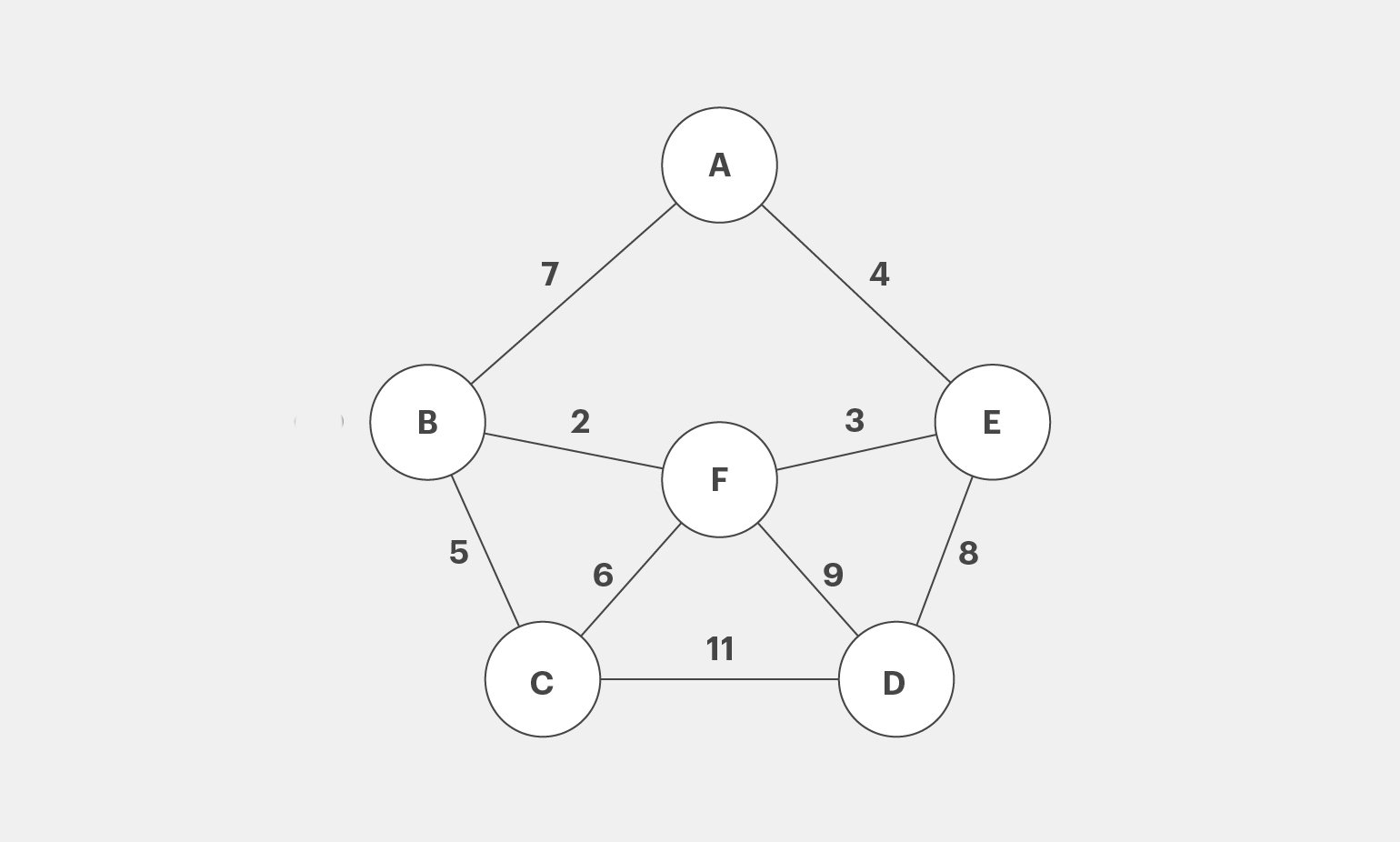
Теперь попробуем найти кратчайший маршрут, скажем, от A до C. Как это сделать? Вроде бы несложно: сравниваем все возможные пути и выбираем самый короткий: A → B → C. Банальный перебор, совсем не rocket science.

Сложности начинаются, когда данных становится слишком много. Если бы городов на нашей карте было больше 26, даже самому мощному компьютеру понадобилось бы несколько миллиардов лет, чтобы просчитать все варианты.

Алгоритм Дейкстры работает иначе: он не перебирает «в уме» все возможные варианты, а строит маршрут пошагово. На каждом шаге алгоритм выбирает наименее отдалённую вершину и двигается к ней, затем к следующей — и так, пока не доберётся до цели.

Вернёмся к нашему графу с городами. Найдём с помощью алгоритма Дейкстры кратчайшие расстояния от А до B, C, D, E и F.

Шаг 1. Установим для каждой вершины первоначальную оценку пути до А. Для самой А оценка равна 0, остальным присвоим бесконечность, так как мы пока не знаем их значения.

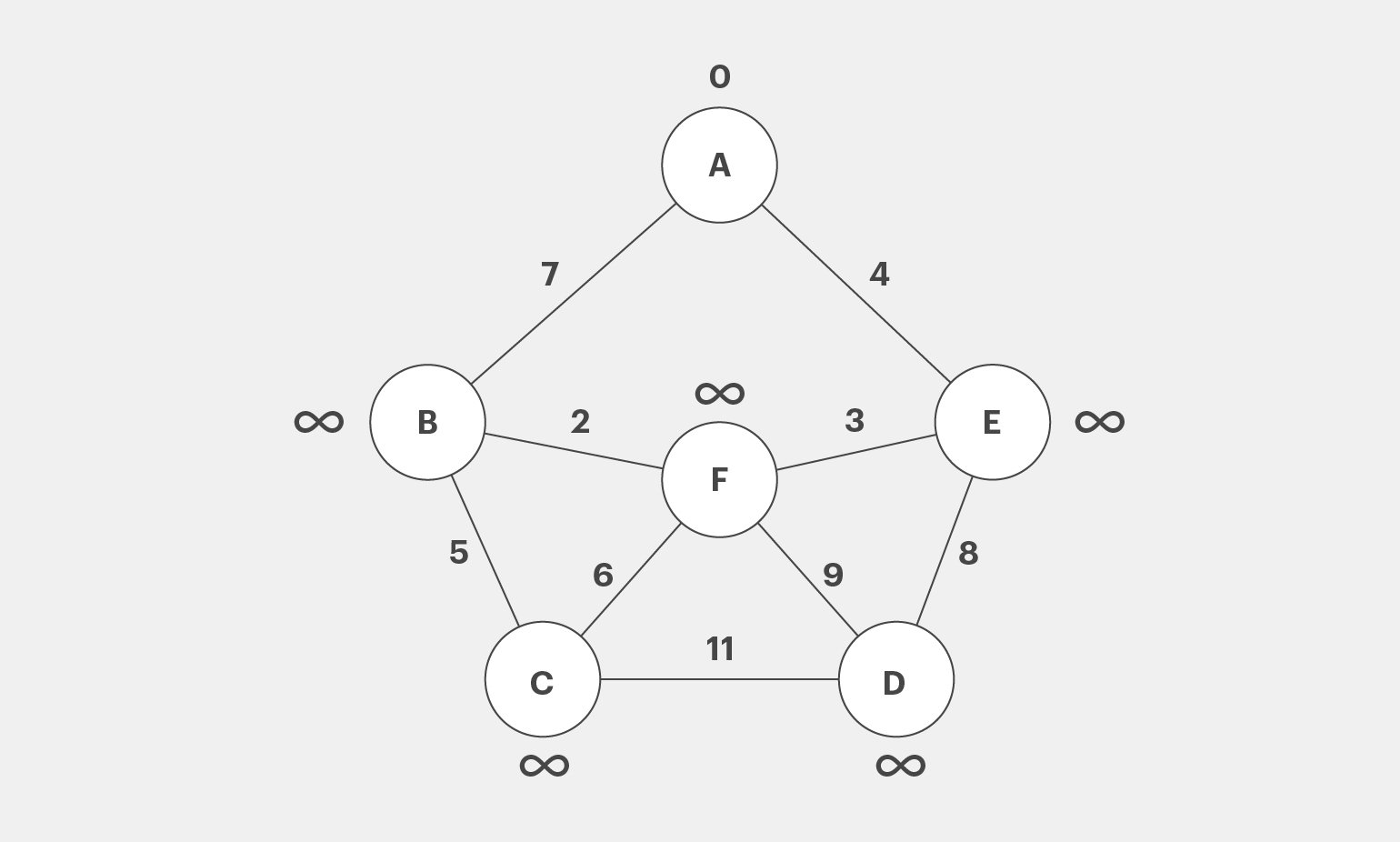
Рассмотрим соседние с A вершины — то есть те, которые связаны с А рёбрами напрямую. Это B и E — их расстояния до А равны 7 и 4 соответственно. Так как эти значения, очевидно, меньше бесконечности, обновим их на схеме. Вершину А будем считать посещённой — закрасим её и больше не рассматриваем.

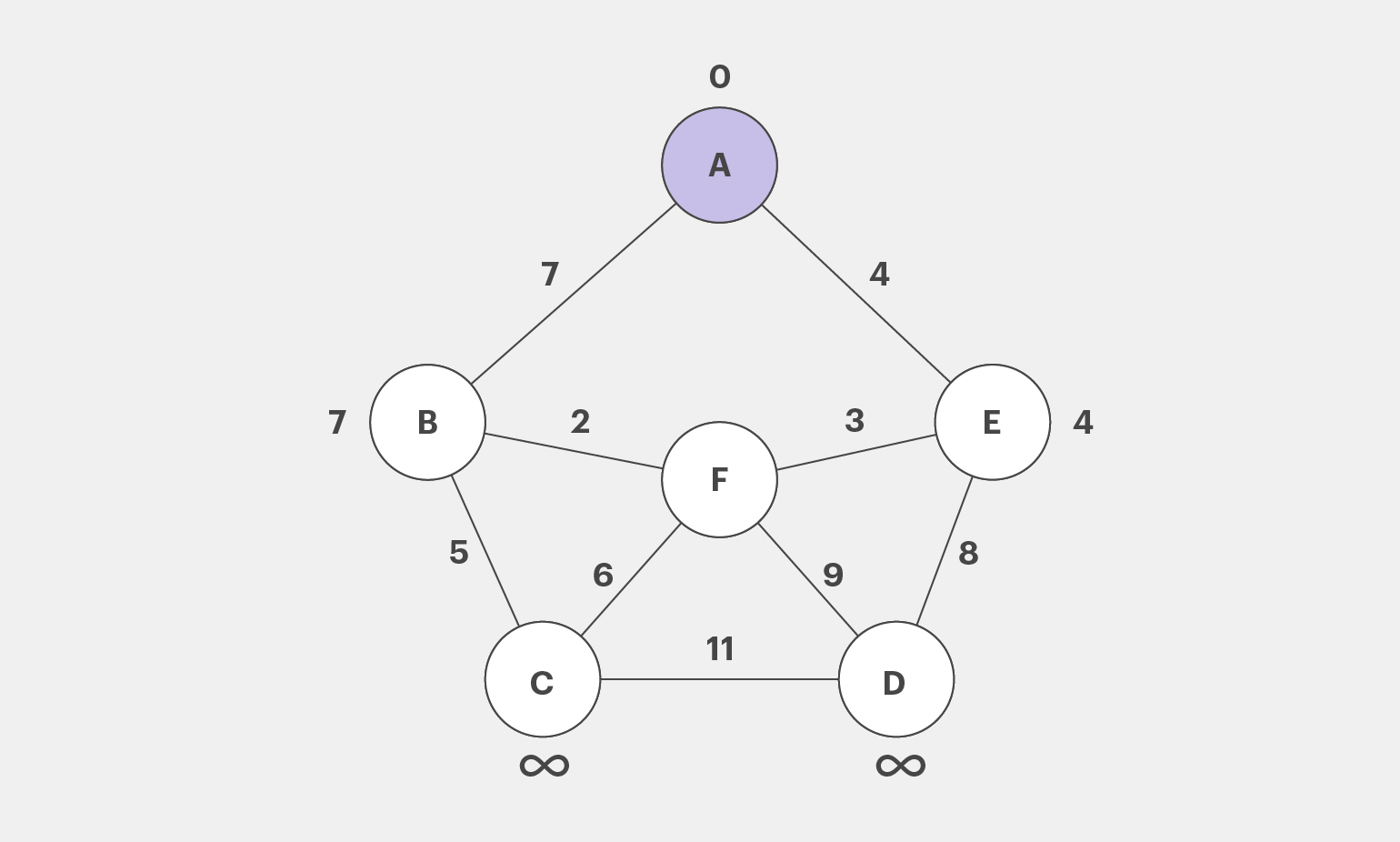
Теперь перейдём к непосещённой вершине с наименьшим расстоянием до А. Это вершина E. Соседние с ней непосещённые вершины — F и D. Их расстояния до А будут равны оценке E (то есть расстоянию от E до А) плюс веса рёбер от E до этих вершин. Получается так:

• Для F: 4 + 3 = 7
• Для D: 4 + 8 = 12

Полученные расстояния меньше предыдущих оценок, поэтому запишем их возле вершин F и D. Вершину E будем считать посещённой. Закрасим её.

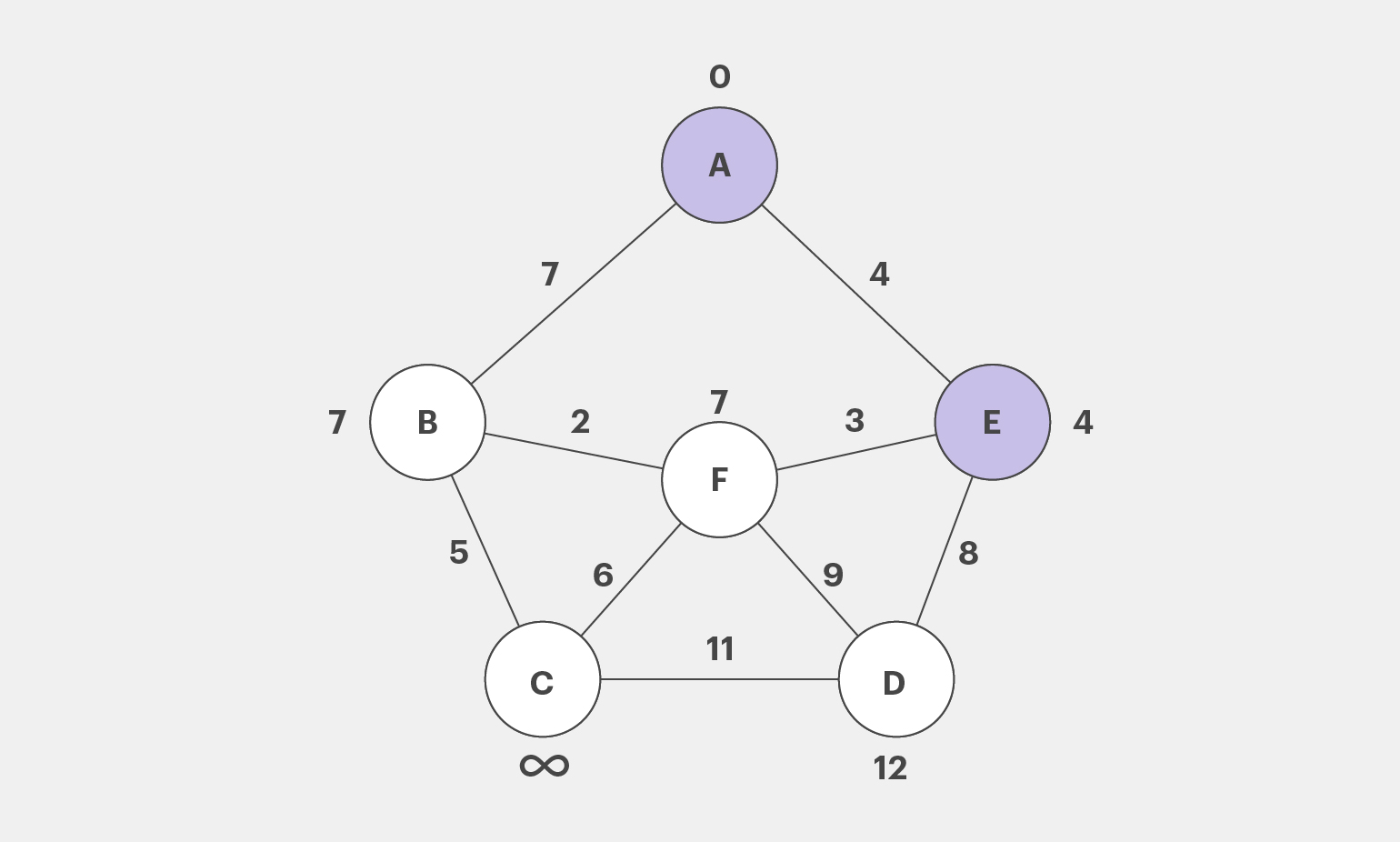
Дальше по аналогии: алгоритм выбирает непосещённые вершины с наименьшей оценкой и считает расстояния от соседних с ней вершин до А. И продолжается это до тех пор, пока алгоритм не вычислит кратчайшие расстояния до А для всех вершин.

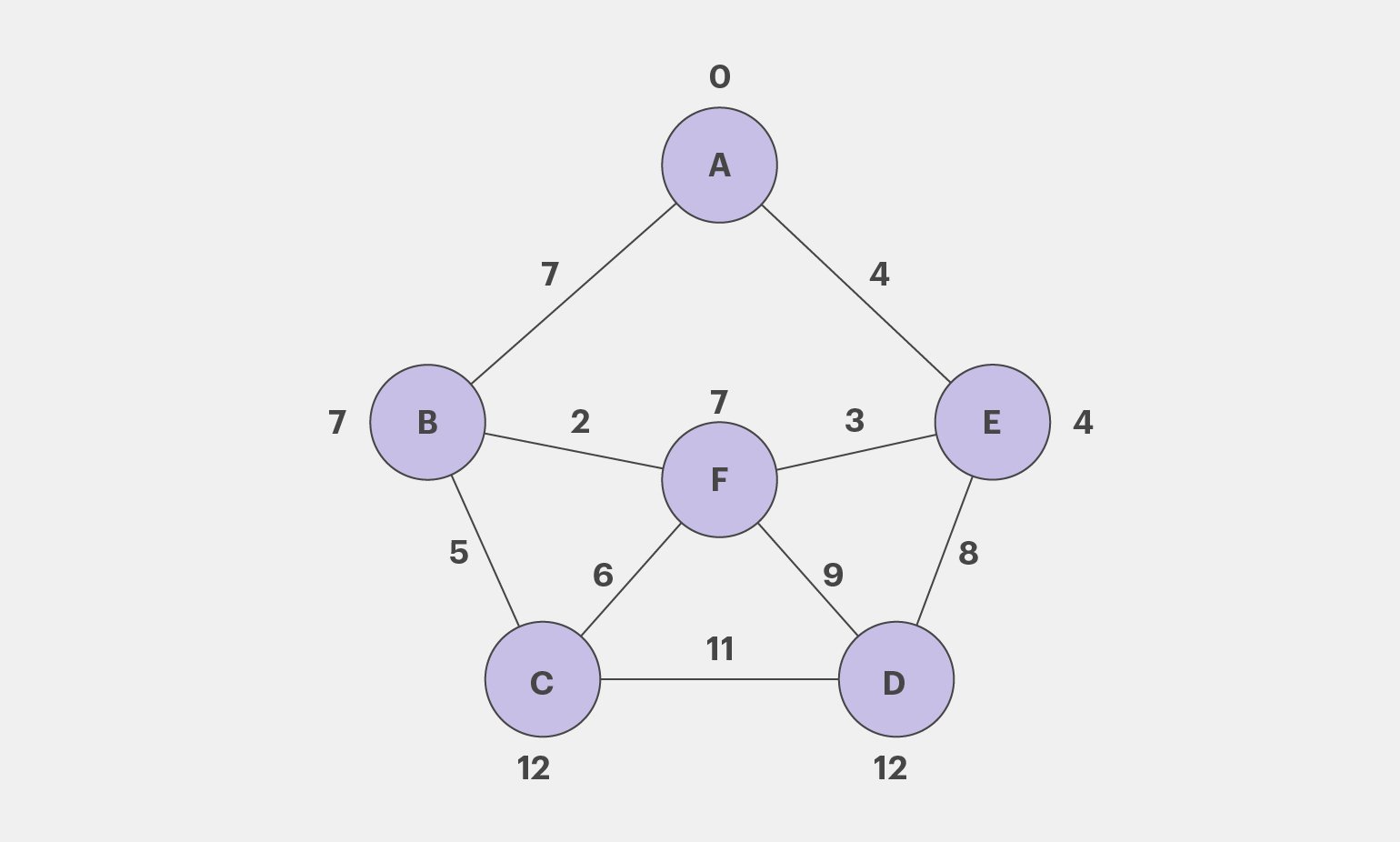
Готово! Теперь мы можем построить кратчайший маршрут от А до любой другой вершины. Например:

• От A до F: A — E — F
• От A до D: A — E — D
• От A до C: A — B — C

Но у алгоритма Дейкстры есть и ограничения: во-первых, он работает только со взвешенными графами — то есть такими, где веса между рёбрами известны заранее. А во-вторых, эти расстояния должны быть неотрицательными.

Как появился алгоритм Дейкстры

Алгоритм поиска кратчайшего пути разработал голландский учёный Эдсгер Дейкстра в 1956 году. В то время он искал способ продемонстрировать возможности нового компьютера ARMAC и искал задачу, которую мог бы решить ARMAC и при этом понятную незнакомым с компьютерами людям.

Дейкстра взял задачу поиска кратчайшего пути и разработал алгоритм её решения. На базе алгоритма он разработал программу построения маршрутов между городами по транспортной карте Нидерландов.

Позже Дейкстра рассказывал:

Пример реализации алгоритма Дейкстры на Python

С теорией разобрались — теперь давайте напишем код, реализующий алгоритм Дейкстры на языке Python. В качестве примера рассчитаем расстояние от вершины A до других вершин в нашем графе.

Для работы нам понадобится heapq — один из модулей стандартной библиотеки Python, предназначенный для работы с кучами. Куча — структура данных, где каждый родительский узел имеет значение, меньшее или равное любому из его дочерних элементов.

Создадим функцию dijkstra с аргументами:

graph — заданный граф;

start — начальная вершина.

Внутри функции создаём словарь distances, чтобы хранить расстояния от начальной вершины до всех остальных. Мы также создаём кучу priority_queue для выбора вершин с наименьшим текущим расстоянием.

import heapq


def dijkstra(graph, start):
    # Инициализация словаря для хранения расстояний
    # до каждой вершины. Сначала все расстояния бесконечны.
    distances = {vertex: float('infinity') for vertex in graph}
   
    # Расстояние до начальной вершины равно 0.
    distances[start] = 0
   
    # Создаём приоритетную очередь для хранения вершин и их расстояний.
    priority_queue = [(0, start)]

Далее алгоритм в цикле обновляет расстояния до соседних вершин до тех пор, пока не найдёт кратчайшие расстояния для всех вершин. Результат выводится в виде словаря, где ключи — вершины, а значения — расстояния до них от точки A.

while priority_queue:
        # Извлекаем вершину с наименьшим расстоянием из очереди.
        current_distance, current_vertex = heapq.heappop(priority_queue)
       
        # Если текущее расстояние до вершины уже больше, чем сохранённое расстояние, игнорируем её.
        if current_distance > distances[current_vertex]:
            continue
       
        # Рассмотрим все соседние вершины текущей вершины.
        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight
           
            # Если найден более короткий путь до соседа, обновим расстояние.
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
   
    return distances

Теперь рассчитаем для нашего графа кратчайшие расстояния от А до остальных вершин. Граф представим в виде словаря, где ключи — вершины, а значения — словари с соседними вершинами и весами рёбер.

# Пример использования:
graph = {
    'A': {'B': 4, 'C': 7},
    'B': {'A': 4, 'D': 2, 'E': 8},
    'C': {'A': 7, 'D': 2, 'E': 5},
    'D': {'B': 2, 'C': 2, 'E': 1,'F': 4},
    'E': {'C': 5, 'D': 1, 'F': 11},
    'F': {'B': 8, 'D': 4, 'E': 11}
}

Вызываем функцию dijkstra с начальной вершиной A и выводим в консоль результат.

result = dijkstra(graph, 'A')
# Выводим результат.
print("Кратчайшие расстояния до каждой вершины:")
for vertex, distance in result.items():
    print(f"До вершины {vertex}: {distance}")

Бинго!

Кратчайшие расстояния до каждой вершины:
До вершины A: 0
До вершины B: 4
До вершины C: 7
До вершины D: 6
До вершины E: 7
До вершины F: 10

Что такое алгоритм А*

Другой известный алгоритм для поиска кратчайшего пути — A* (читается как «А звезда» или «А стар»). По сути, это расширение алгоритма Дейкстры с дополнительными функциями для улучшения скорости. Разработали A* в 1968 году, используют — до сих пор в разных областях: от робототехники до навигации и геймдева.

Так же как и алгоритм Дейкстры, A* ищет расстояние от начальной точки до конечной. Но, в отличие от последнего, он учитывает не только расстояние от текущей точки до начальной, но и эвристическую оценку этого расстояния. В данном контексте «эвристическая» означает «примерная»: функция не определяет точное расстояние от точки до цели, но подсказывает алгоритму приблизительную величину.

Например, нам нужно найти кратчайший путь из города А в город В на карте. В качестве эвристики мы можем использовать расстояние «по прямой линии» (то есть «евклидово расстояние») от текущей точки до точки B. Это позволит оценить длину пути между текущей точкой и целью.

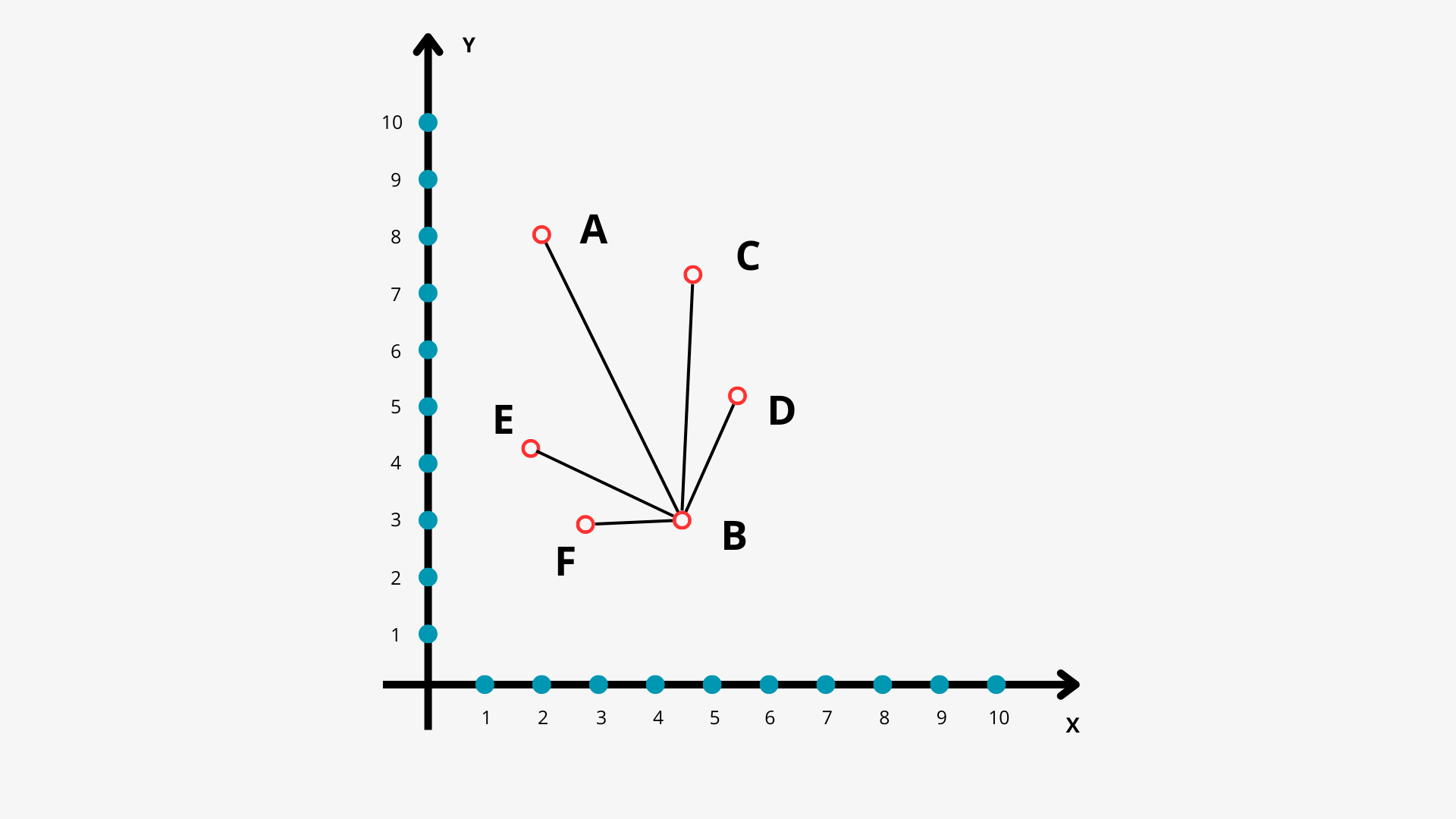
На графике выше изображены эвристические расстояния от промежуточных точек до конечной точки на карте, без учёта существующих дорог.

Ещё одна популярная эвристика — манхэттенское расстояние. Её название происходит от системы улиц на острове Манхэттен в Нью-Йорке. Это сеть улиц, которые пересекаются под прямым углом, что делает её похожей на таблицу. Чтобы добраться от одной точки до другой, приходится двигаться вдоль улиц. Если представить эти улицы в виде координатной сетки, мы можем двигаться только вдоль осей X и Y, но не по диагонали.

Если у нас есть две точки с координатами (x1, y1) и (x2, y2), то манхэттенское расстояние между ними (M) вычисляется по следующей формуле:

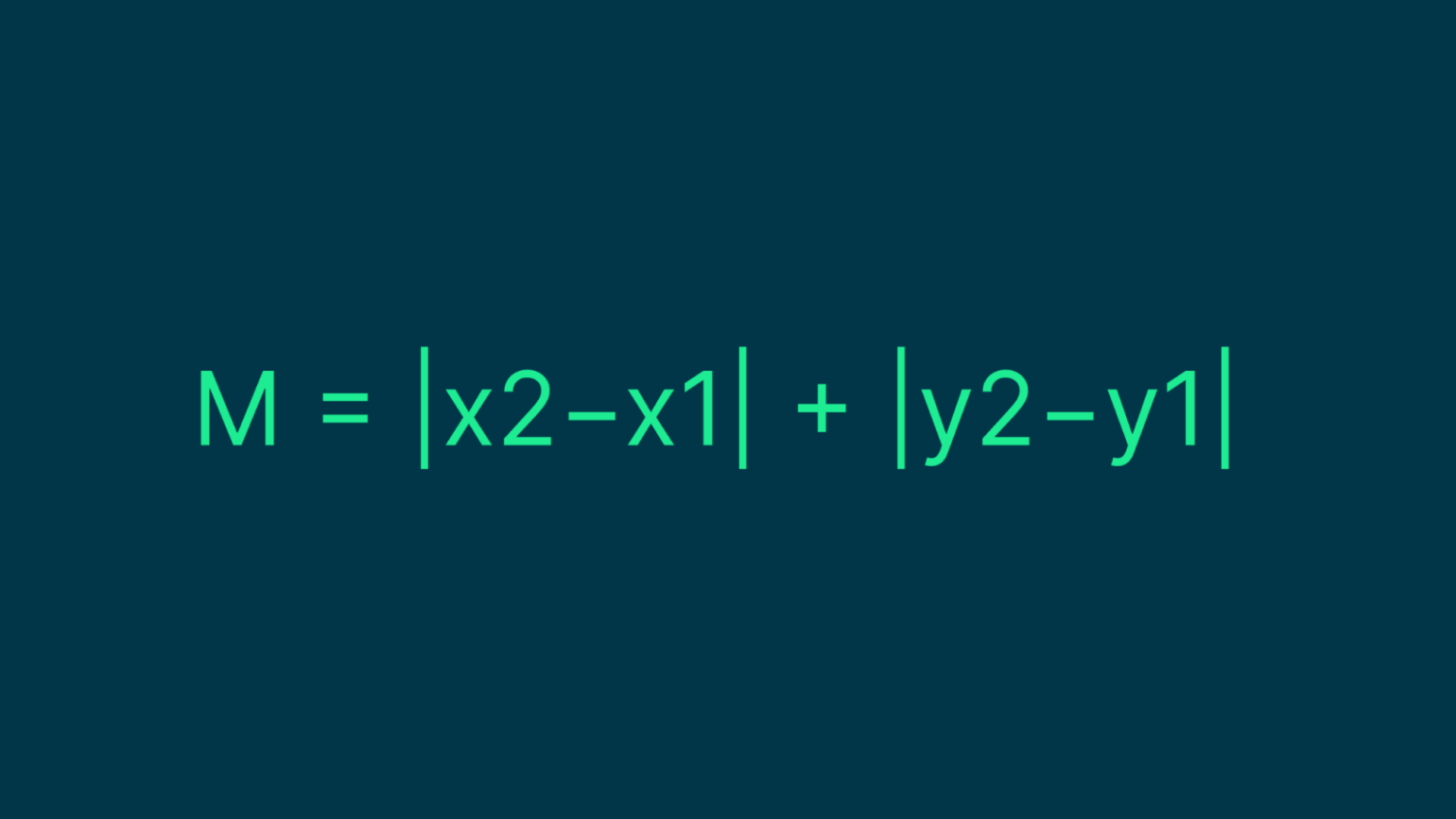
Попробуем разобраться на примере. Допустим, у нас есть точка A с координатами (2, 8) и точка B с координатами (4, 3).

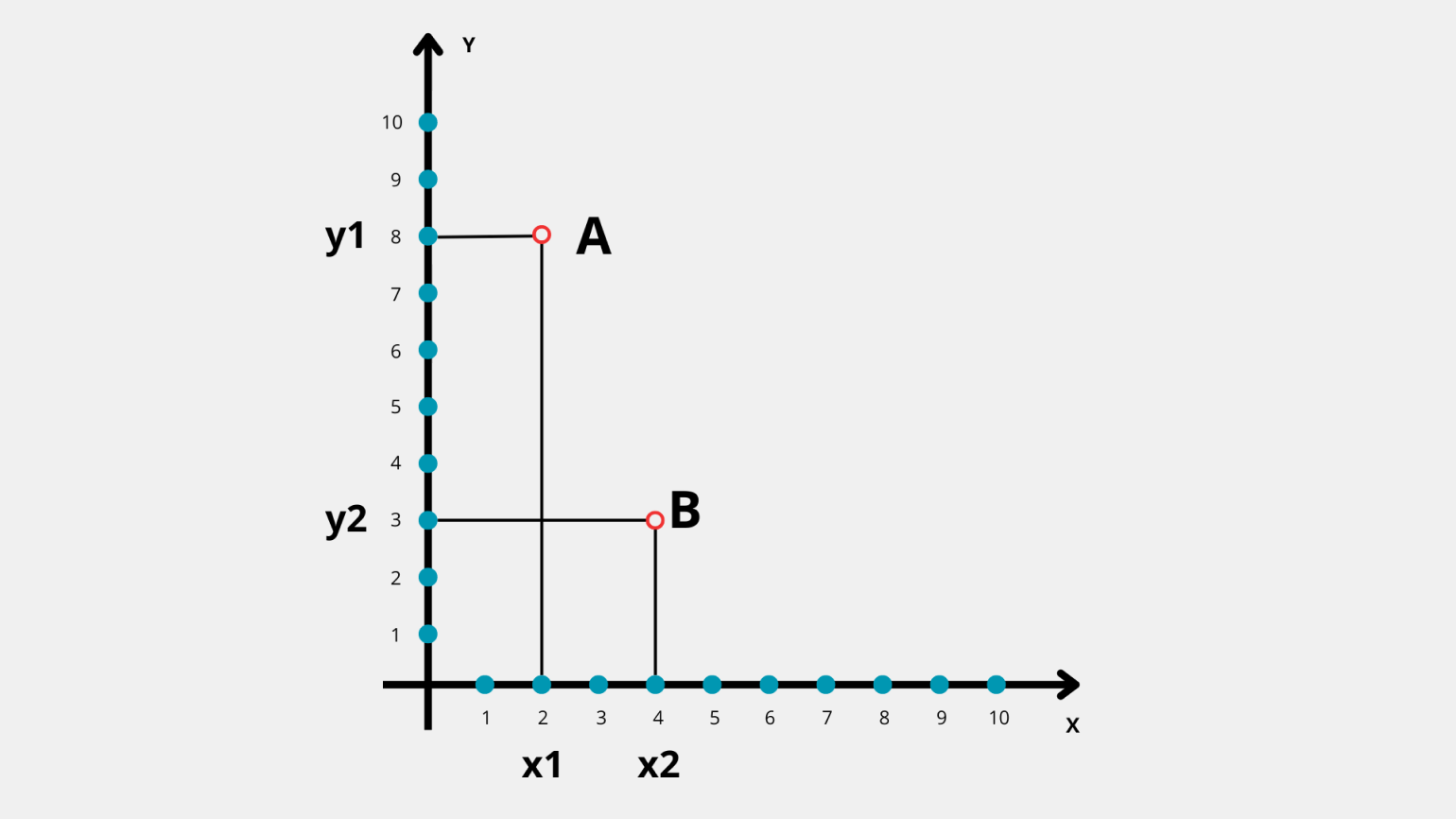
Подставляем координаты в формулу — получается, манхэттенское расстояние равно M = ∣4−2∣ + ∣3−8∣ = 2 + 5 = 7.

Основная идея алгоритма A* — это определение двух значений для каждой вершины в графе:

• g(n) — длина пути от начальной вершины до текущей вершины n.
• h(n) — эвристическая оценка длины от текущей вершины n до цели.

На каждом шаге алгоритм A* выбирает вершину с наименьшей суммой g(n) + h(n) и исследует её соседей. Это продолжается до тех пор, пока алгоритм не достигнет конечной цели.

Реализация алгоритма А* на Python

Попробуем написать A* на Python для графа с эвристикой в виде манхэттенского расстояния. Здесь функция manhattan_distance вычисляет манхэттенское расстояние между двумя точками, а astar реализует алгоритм A* с использованием этого расстояния.

import heapq


# Функция для вычисления манхэттенского расстояния между двумя точками
def manhattan_distance(point1, point2):
    return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1])

Реализация алгоритма A*:

def astar(grid, start, goal):
    # Инициализация словарей для хранения стоимостей и предыдущих точек
    cost = {start: 0}
    came_from = {start: None}


    # Приоритетная очередь для хранения точек и их оценок (приоритетов)
    priority_queue = [(0, start)]


    while priority_queue:
        # Извлечение точки с минимальной оценкой
        current_cost, current_point = heapq.heappop(priority_queue)
               
        # Если достигнута целевая точка, завершаем алгоритм
        if current_point == goal:
            break


        # Рассмотрение соседних точек
        for neighbor in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
            x, y = current_point[0] + neighbor[0], current_point[1] + neighbor[1]
           
            new_cost = cost[current_point] + 1 # Стоимость перемещения на одну ячейку
           


            # Проверка на наличие препятствия и обновление стоимости, если новый путь короче
            if 0 <= x < len(grid) and 0 <= y < len(grid[0]) and grid[x][y] == 0:
                if (x, y) not in cost or new_cost < cost[(x, y)]:
                    cost[(x, y)] = new_cost
                    priority = new_cost + manhattan_distance((x, y), goal)  
# Оценка для приоритета
                    heapq.heappush(priority_queue, (priority, (x, y)))
                    came_from[(x, y)] = current_point

Восстановление пути:

path = []
    current = goal
    while current:
        path.append(current)
        current = came_from[current]
    path.reverse()


    return path

Выполнение алгоритма A*. Определение сетки 5 × 5. Препятствия обозначаются единицами в сетке.

grid = [
    [0, 0, 0, 0, 0],
    [0, 1, 1, 0, 0],
    [0, 0, 0, 1, 0],
    [0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0]
]


# Начальная и конечная точки
start = (0, 0)
goal = (4, 4)


result_path = astar(grid, start, goal)


# Вывод результата
print("Путь от A до B:")
for point in result_path:
    print(point)

В результате выполнения получим:

Путь от A до B:
(0, 0)
(0, 1)
(0, 2)
(0, 3)
(0, 4)
(1, 4)
(2, 4)
(3, 4)
(4, 4)

Этот код реализует A* для поиска кратчайшего пути в заданной сетке с использованием манхэттенского расстояния в качестве эвристической функции. В результате он выводит кратчайший путь от точки А до B.

Сравнение алгоритмов Дейкстры и A*

Выбор между этими алгоритмами зависит от конкретной задачи и доступной информации.

Сравним их:

• Алгоритм Дейкстры используется для нахождения кратчайшего пути от начальной вершины графа ко всем остальным. Алгоритм A* используется для нахождения кратчайшего пути от начальной вершины к заданной, учитывая эвристическую оценку расстояния.
• Алгоритм Дейкстры рассматривает все вершины равнозначно и всегда выбирает вершину с наименьшим расстоянием до неё. Алгоритм A*, кроме этого, дополнительно использует эвристику. Это делает его более эффективным для больших графов или когда есть информация о приблизительной величине дистанции до цели.
• Алгоритм Дейкстры может быть медленным для больших графов, так как исследует все вершины. Алгоритм A* в больших графах работает быстрее благодаря эвристике, которая позволяет сократить количество рассматриваемых вершин.

Таким образом, алгоритм Дейкстры будет эффективнее там, где нужно найти кратчайшие пути от одной вершины ко всем остальным и нет информации о примерной дистанции до цели. Если есть эвристическая информация, которая может помочь ускорить поиск, то лучшим выбором будет A*.