Сократ должен умереть: от Аристотеля и силлогизмов до Python и AI
Попробуем научить компьютер делать умозаключения, потому что... а почему бы и нет? До восстания машин осталось 10... 9... 8...

Силлогизм — это рассуждение, которое состоит из трёх простых высказываний вида «А есть Б», два из которых называются посылками, а третье — заключением.
Теорию силлогизмов придумал древнегреческий философ Аристотель, а до совершенства их довели средневековые схоласты.
Классический пример силлогизма:
- Все люди смертны (первая посылка).
- Сократ — человек (вторая посылка).
- Следовательно, Сократ смертен (заключение).
Суперсила силлогизмов заключается в универсальности их конструкции. В ней можно менять содержимое: людей заменить на кошек, смертность на вредный характер, а Сократа — на вашего кота Стёпу; при этом из истинности посылок по-прежнему будет следовать истинность заключения.

Есть 256 видов силлогизмов, и все их тщательно изучали в средневековых университетах и монастырях. Школяры-схоласты мучились с ними ничуть не меньше, чем нынешние студенты-программисты с бинарными деревьями и хеш-таблицами.
Силлогизмы в кружочках
Силлогизмы удобнее всего представлять в виде диаграмм (или кругов) Эйлера. Каждая окружность обозначает один термин из силлогизма. В нашем силлогизме таких терминов три: «смертные», «люди», «Сократ».

Взаиморасположение окружностей (пересечение, непересечение и полное вхождение) выражает разные отношения между терминами.
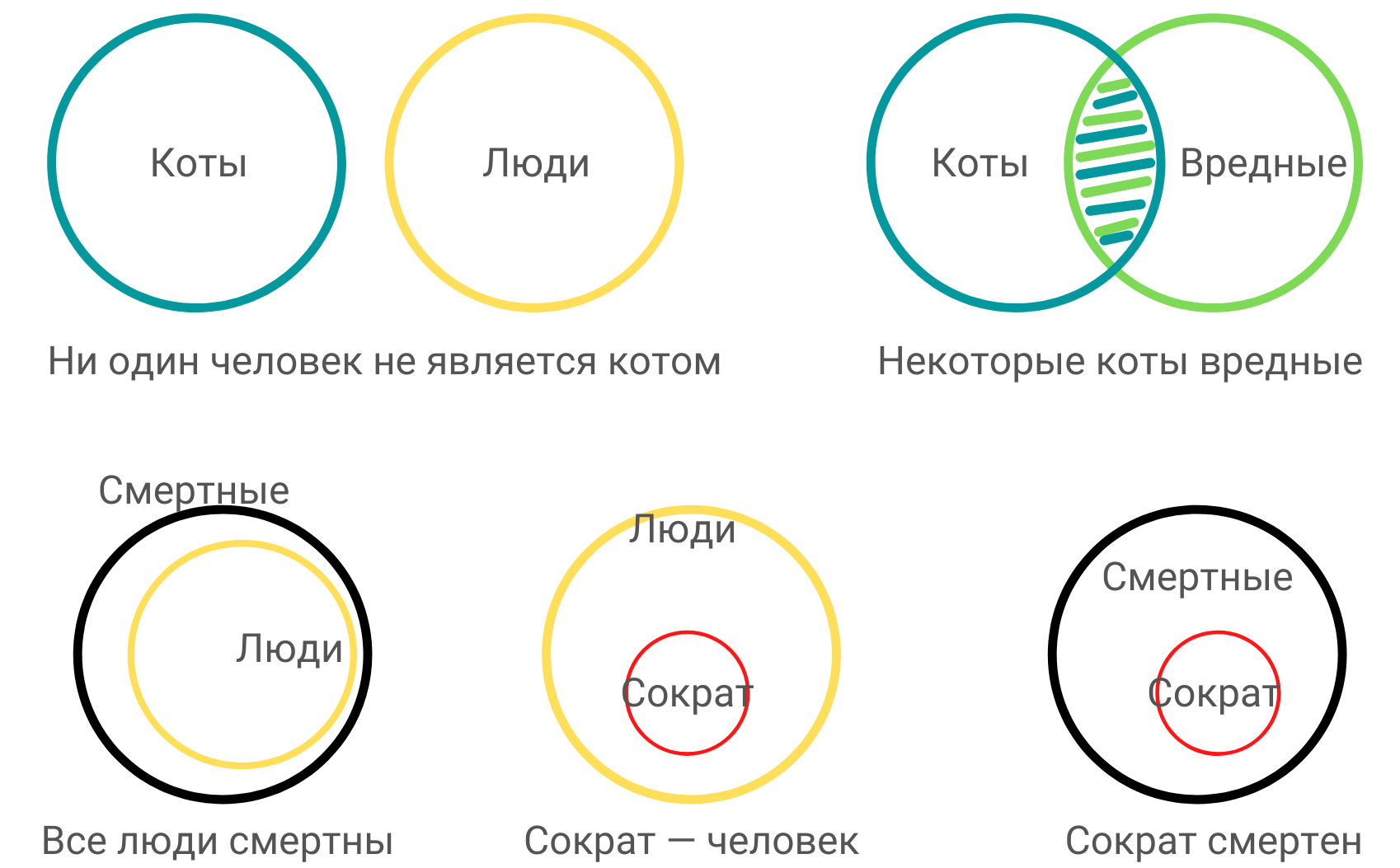
Силлогизмы до сих пор используются в тестах на IQ и логическое мышление. Вот пример.
Посылки:
- Все ракеты — это трубы.
- Некоторые трубы являются дудочками.
- Некоторые дудочки — это брюки.
- Все брюки — это штаны.
Заключения:
- Некоторые штаны — дудочки.
- Некоторые брюки — ракеты.
- Некоторые дудочки — это ракеты.
- Некоторые трубы — это ракеты.
Вопрос: какие из заключений истинны, если правдивы посылки?
Вооружённые кружочками Эйлера, мы легко расщёлкаем эту задачу.
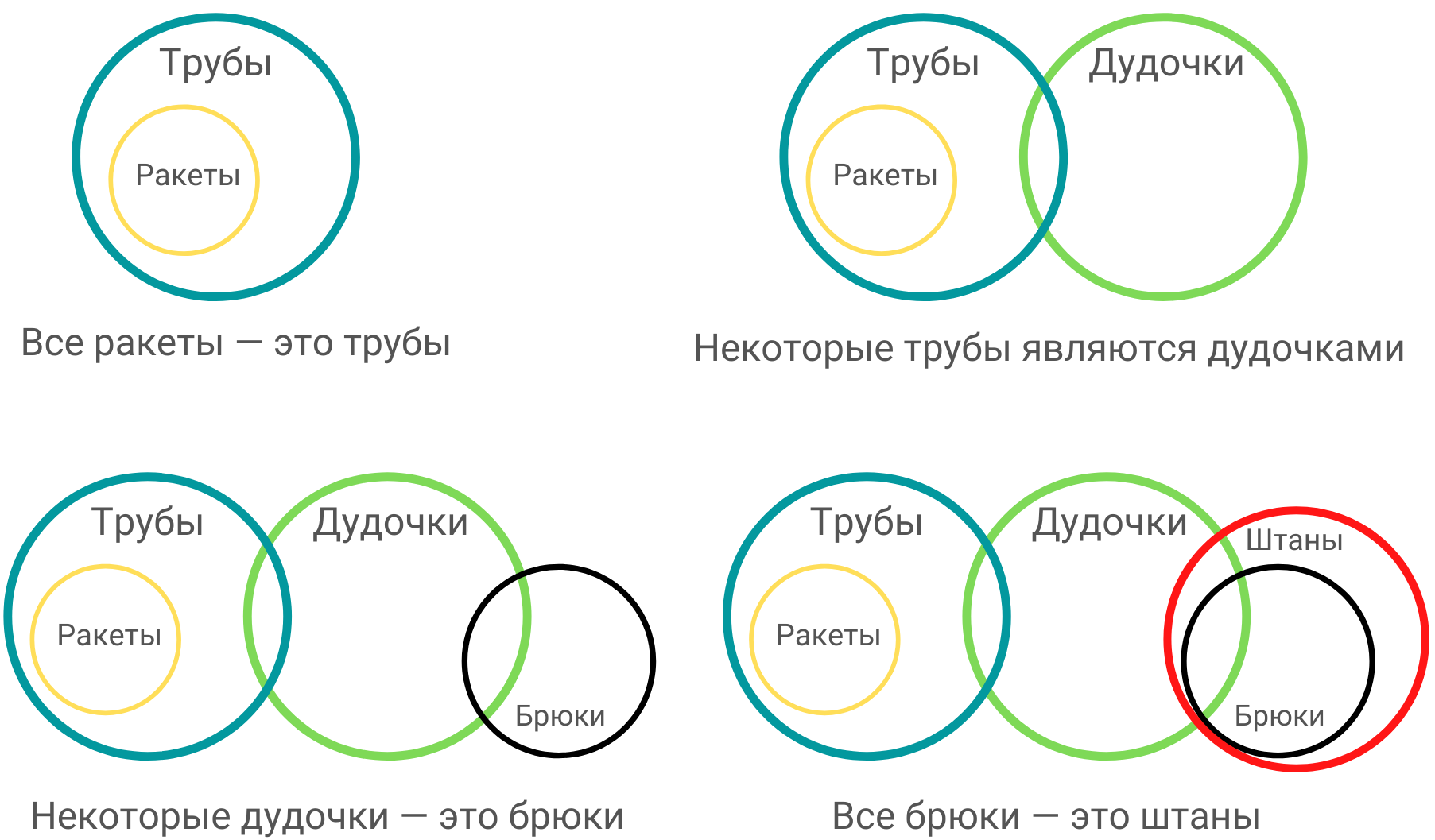
При составлении диаграмм главное — ничего не выдумывать, строго придерживаться того, что указано в посылках. Если в посылке ничего не сказано об отношениях ракет и дудочек, то соответствующие им кружочки не пересекаются.
Проверяем наши заключения:
- «Некоторые штаны — дудочки». Красная и зелёная окружности пересекаются — значит, исходное заключение истинно.
- «Некоторые брюки — ракеты». Не пересекаются. Ложь.
- «Некоторые дудочки — это ракеты». Ложь.
- «Некоторые трубы — это ракеты». Истина.
Но цветные окружности — это для людей, а компьютеру нужны биты, байты и код. Как быть?
Как подружить силлогизм и компьютер. Два подхода
Чтобы компьютер выдал нам ответ, похожий на результат логического размышления, нужна программа (спасибо, Кэп!). К написанию таковой возможны два подхода: содержательный и формальный.
Содержательный подход заключается в том, что мы создаём в памяти компьютера приближённую копию участка реальности.
У компьютера в памяти будут модели «смертных» и «людей», а также модель Сократа. Отношения между всеми моделями должны быть похожими на те, которыми связаны их прообразы.

И модели, и отношения надо будет задать соответствующими командами. Когда мы запустим программу, машина сначала исполнит команды, описывающие модели и их отношения, а затем команду по вычислению результата. Способ получения результата (но не сам результат) тоже надо будет указать.
Основная проблема содержательного подхода в том, что нет никакой гарантии, что модель всегда будет вести себя так же, как прототип. А улучшать модель, чтобы она была ближе к реальности, — чем дальше, тем накладнее.
Формальный подход: мы говорим компьютеру «вот эту последовательность символов считать истинной, а другую считать ложной» и загружаем в него правила работы только с ложью и истиной, то есть логику. Мы не моделируем реальность и не вникаем в суть посылок, а работаем только с последовательностями символов.
Этот подход компьютерам ближе: формальная логика, оперирующая понятиями истинности и ложности высказываний без обращения к их содержанию, имеет много общего с вычислениями в двоичной системе счисления. А эта система как раз и реализована в схемах, из которых компьютеры состоят.
Напишем на Python две программы, по-разному имитирующие рассуждение Аристотеля. Ведь ещё мудрец Лао-цзы говорил: «Дорога к тысячам ИИ начинается со строчки import this». (Или это был Эндрю Ын?) Код можно написать в любом онлайн-интерпретаторе Python или в Google Colab.
Формальная имитация силлогизма
C помощью метода def мы определим функцию, которую назовём, разумеется, aristotle. Она принимает три аргумента: две посылки (prem_1, prem_2) и заключение conc.
def aristotle(prem_1, prem_2, conc):
if prem_1['Истинность'] == True and prem_2['Истинность'] == True:
conc['Истинность'] = True
return f'Заключение «{conc["Текст"]}» истинно'
else:
return 'Не могу сказать точно'Если обе посылки истинны, то функция присваивает значение True истинности заключения conc и возвращает соответствующую фразу. Если же хотя бы одна посылка ложна, то функция сообщает, что ничего сказать точно не может.
Далее мы объявляем посылки и заключение:
premise_1 = {'Текст':'Все люди смертны', 'Истинность': True}
premise_2 = {'Текст':'Сократ -- человек', 'Истинность': True}
conclusion = {'Текст':'Сократ смертен'}Это словари, состоящие из пар вида «ключ-значение». Под ключом 'Текст' мы храним текст каждой посылки, а под ключом 'Истинность' — её правдивость.
И текст посылки, и её истинность мы задаём сами — у нас, напомним, формальный подход.
У двух первых посылок истинность равна True, а у заключения такого ключа нет, поскольку мы не знаем, истинно ли оно.
Запускаем функцию на исполнение и получаем результат:
aristotle(premise_1, premise_2, conclusion)
>>> Заключение «Сократ смертен» истинно
print(conclusion['Истинность'])
>>> TrueУ формального подхода — свои недостатки. Например, если поменять наши посылки на «Некоторые кошки чёрные» и «Солнце встаёт на востоке», Сократ всё равно останется смертен: нашей функции безразлично содержание, ей важны только значения True или False. По сути, она работает только с ними, а посылки и высказывания — это не более чем декорации для этих значений.
Почти содержательная имитация
Моделями смертных и людей у нас будут переменные-списки Python, а Сократ станет одноимённой строкой.
Напишем функцию, которую назовём, понятное дело, syllogism:
def syllogism(men, mortals, sokrat):
# Сократ человек
men.append(sokrat)
# Все люди смертны
mortals.extend(men)
# Сократ смертен: True или False
return f"Сократ смертен: {sokrat in mortals}"Функция принимает в качестве своих аргументов три переменные men, mortals, sokrat. Затем она присоединяет «Сократа» к людям с помощью метода .append () и добавляет список людей к списку смертных с помощью .extend (). После этого возвращает строку с результатом проверки: находится ли «Сократ» среди смертных (оператор in).
Зададим переменные и запустим с ними нашу функцию. Списки пустые, потому что мы не сможем реально занести туда всех смертных или хотя бы всех людей.
sokrat = 'Сократ'
mortals = []
men = []
syllogism(men, mortals, sokrat)
>>> Сократ смертен: TrueПреимущества такой функции в том, что здесь мы не задавали значения True и False вручную и результат был вычислен из соотношения между самими моделями, а не между какими-то их атрибутами.
Но пустые списки не очень похожи на смертных и человечество, а строка — на Сократа, даже если и названа так же. Кроме того, крайне важна последовательность реализации посылок: если поменять строки в функции местами, то она будет выдавать False.
Эти претензии глубже, чем кажется на первый взгляд, и вообще-то вопросов гораздо больше. Но так или иначе все они сводятся к главному: как мы вообще научим машину мыслить, если сами не знаем, что такое мышление, разум, интеллект?
Исследователи ИИ отвечают на этот вопрос примерно так: «Да, мы не знаем, но как раз с помощью ИИ и надеемся узнать». Хммм… Вам тоже кажется, что тут какой-то подвох?
Кстати, что там с ИИ?
Ещё в XVII веке Томас Гоббс заявил, что «рассуждение — это не более чем подсчитывание». Поэтому в середине 1950-х годов, на заре компьютерной эры, учёные были полны оптимизма: ведь компьютеры уже тогда считали гораздо лучше людей.
Так, организаторы Дартмутского семинара, который считается местом рождения ИИ, были уверены, что в течение одного лета группа из десяти учёных сможет «существенно продвинуться» в понимании того, «как обучить машины использовать естественные языки, формировать абстракции и концепции, решать задачи, сейчас подвластные только людям, и улучшать самих себя».

Достичь этих целей, как мы знаем, не удалось ни за одно лето, ни за десять. Более того, искусственный интеллект пережил две длинные зимы, когда интерес к нему почти пропал. Но также мы знаем, что этот интерес не угас окончательно, а сейчас, напротив, разгорается с новой силой.
Если вы разделяете энтузиазм или, напротив, полны алармизма и хотите знать, откуда прилетит какая-нибудь технологическая сингулярность, — добро пожаловать на курс «Философия искусственного интеллекта», созданный Skillbox совместно с Московским государственным университетом.
Студентам здесь открывается общая картина современного ИИ. Они знакомятся с основными идеями и концепциями, с ним связанными, оценивают его возможности и влияние на нашу жизнь, а также перспективы развития ИИ.
По одной из гипотез с этого курса, ментальные процессы и явления (мышление, сознание, интеллект) происходят в физических системах. Они могут происходить в такой физической системе, как мозг, а могут — в такой, как компьютер.
Может статься, что появление сознания — это закономерный этап эволюции информационных систем, которые ранее были физическими, то есть подчинялись только законам физического бытия. Если нефизические качества (например, ментальные) возникают в процессе усложнения физических систем, то почему бы другим подобным системам, развиваясь, их тоже не порождать?
Итак, будущее за ИИ: True или False? Давайте выяснять, пока есть время. 5… 4… 3…