Рациональные числа: определение, свойства и примеры

Миром правят числа! Так однажды сказал Пифагор, и у нас нет оснований с ним спорить. Вопрос лишь в том, что это за числа. Например, натуральными числами вы никогда не опишете отрицательный баланс на карточке или, скажем, точный показатель скорости света. Здесь нужна артиллерия помощнее — то есть рациональные числа.

Сегодня мы узнаем, что это за числа такие, зачем они нужны и как появились. Статья будет полезна не только студентам, штудирующим базу перед экзаменами, но и новичкам в IT — в конце мы посмотрим, как работать с рациональными числами на языке Python.

Из этой статьи вы узнаете:

• что такое рациональные числа;
• чем они отличаются от остальных;
• какие у них есть свойства;
• как работать с рациональными числами в Python;
• резюме: что нужно запомнить.

Что такое рациональные числа

Рациональные числа — это все числа, которые можно представить в виде дроби m/n, где числитель m — это целое число, а знаменатель n — натуральное. Множество рациональных чисел обозначается латинской буквой Q.

Например, число 0,5 можно представить как дробь 5/10 или ½, а значит, оно является рациональным. Математически это записывается как 0,5 ∈ Q.

Любое целое число тоже можно считать рациональным — ведь мы можем представить его в виде дроби. Например, число 5 можно записать как 5/1. Технически это будет неотличимо от деления 5 на 1, в результате которого получится та же самая пятёрка.

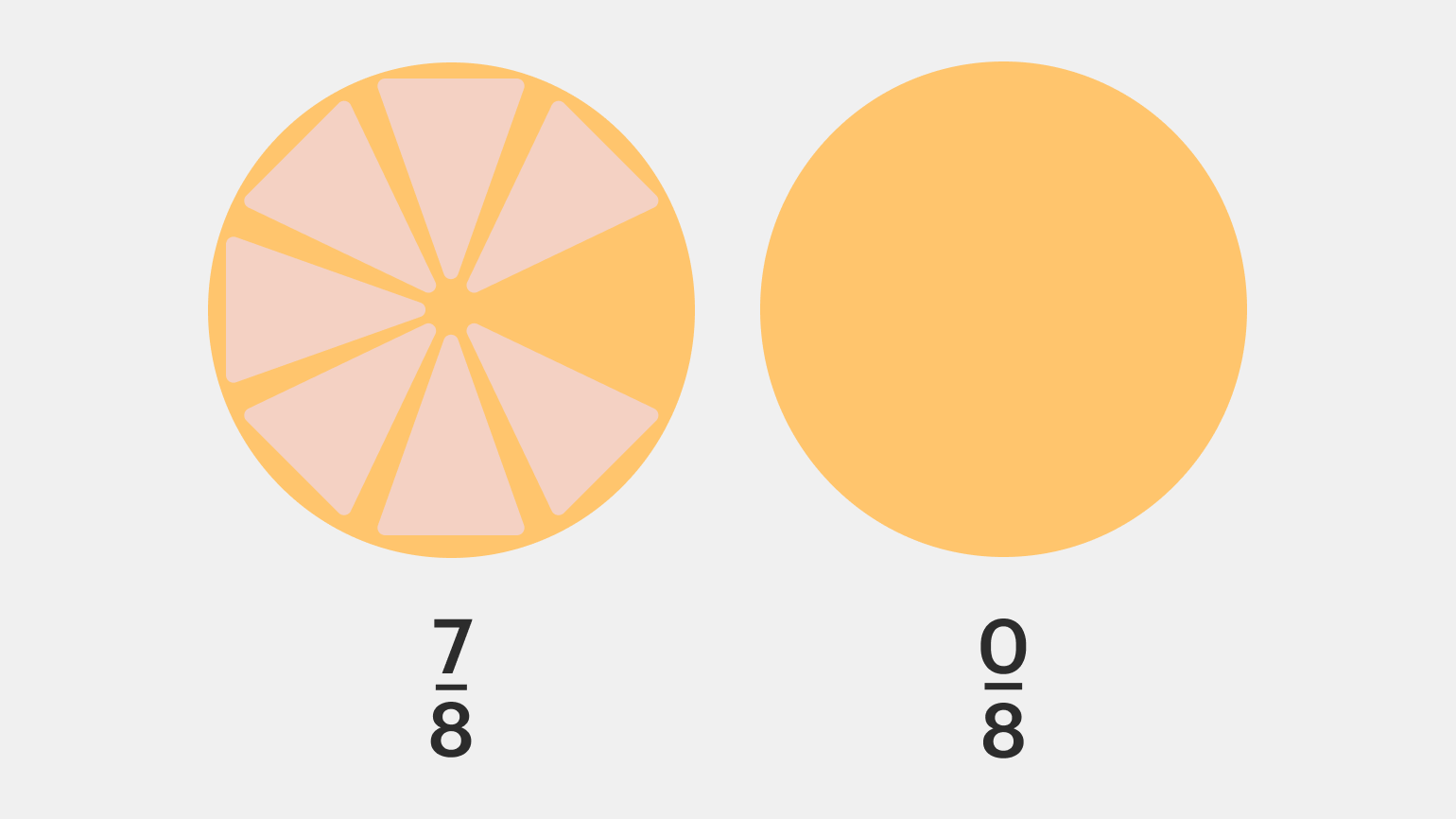
Ноль также относится к рациональным числам, потому что его мы тоже можем представить в виде дроби. Так как на ноль делить крайне не рекомендуется, знаменатель у ноля тоже не может быть меньше единицы. Проиллюстрировать это можно на примере пиццы: сначала у нас было 7 из 8 кусков, то есть дробь 7/8, а когда всё съели — стало 0/8:

Бесконечные периодические дроби также относятся к рациональным числам. Например, если мы возьмём дробь 1/7 и попытаемся перевести её в обычный вид — то есть разделим 1 на 7, — то получим 0,14285714285714… Последовательность после запятой (период) 142857 будет повторяться до бесконечности, но при обратной операции мы снова получим дробь 1/7, а значит, это также относится к рациональному множеству.

Примеры рациональных чисел:

• Целое положительное натуральное число 1 — это 1/1.
• Целое число 0 — это 0/1.
• Целое отрицательное число −5 — это −5/1.
• Десятичная дробь 0,25 — это 25/100.
• Отрицательная десятичная дробь −0,75 — это −75/100.
• Смешанное число 3,25 — это 13/4.
• Бесконечная периодическая дробь 0,333… — это 1/3.

Чем рациональные числа отличаются от остальных

Чтобы лучше разобраться в специфике рациональных чисел — краткий ликбез по математическим множествам.

Начнём с натуральных чисел. К ним относятся все положительные числа: от 1 до бесконечности — ноль в этот список не входит. Натуральные числа мы используем, чтобы посчитать что-то материальное: одна монета, два фломастера, пять машин. Этот вид чисел — самый древний, его использовали для расчётов ещё первобытные племена.

Целые числа — все натуральные числа, противоположные им (то есть отрицательные), а также ноль. Считается, что такие числа впервые стали использовать в Древнем Китае и Древней Индии для математического обозначения долга.

Следующее множество — рациональные числа. Это все натуральные и целые числа, а также дроби: обыкновенные, конечные десятичные и бесконечные периодические. Периодические — это такие дроби, где одна или группа цифр после запятой повторяются, например 0,161616… Если этого повтора нет, то число уже зовётся иррациональным.

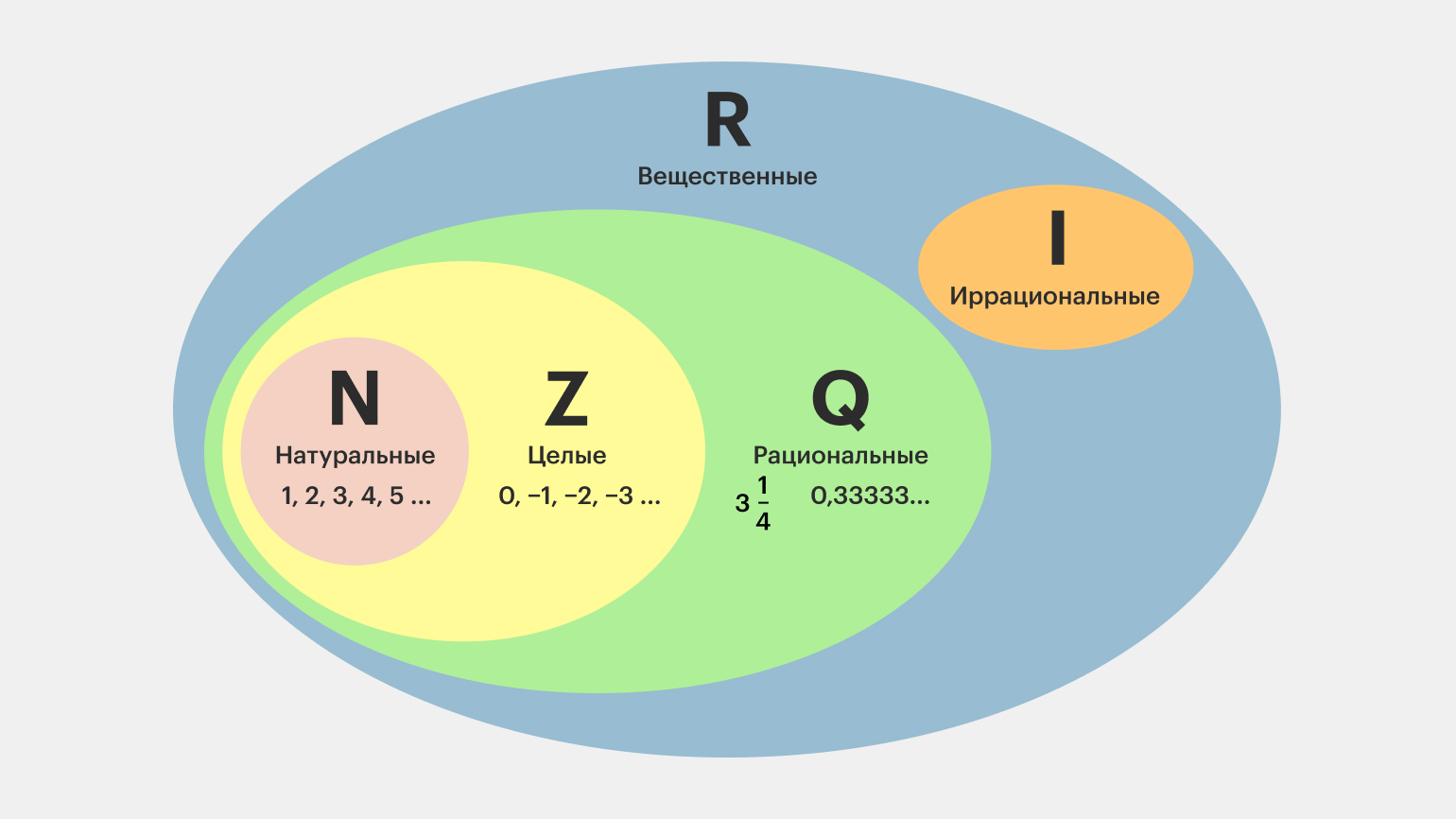
Иррациональные и рациональные числа, в свою очередь, образуют новое множество — вещественные числа. Визуально это можно представить так:

Свойства рациональных чисел

Как и у любых других объектов в математике, у рациональных чисел есть свои свойства. Во всех примерах ниже a, b и c являются рациональными числами.

Свойства сложения

1️⃣ Переместительное свойство. От перемены мест слагаемых сумма не меняется:

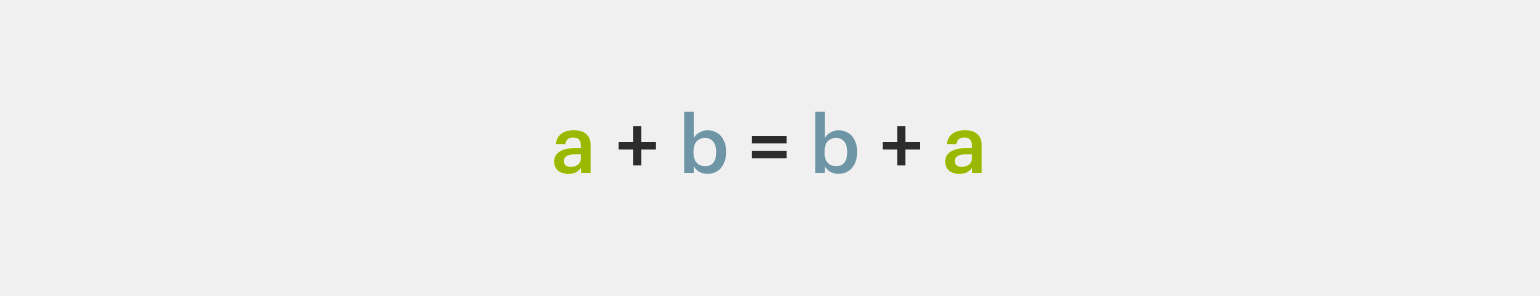
2️⃣ Сочетательное свойство. Чтобы к рациональному числу прибавить сумму двух чисел, нужно к первому числу прибавить и первое, и второе число:

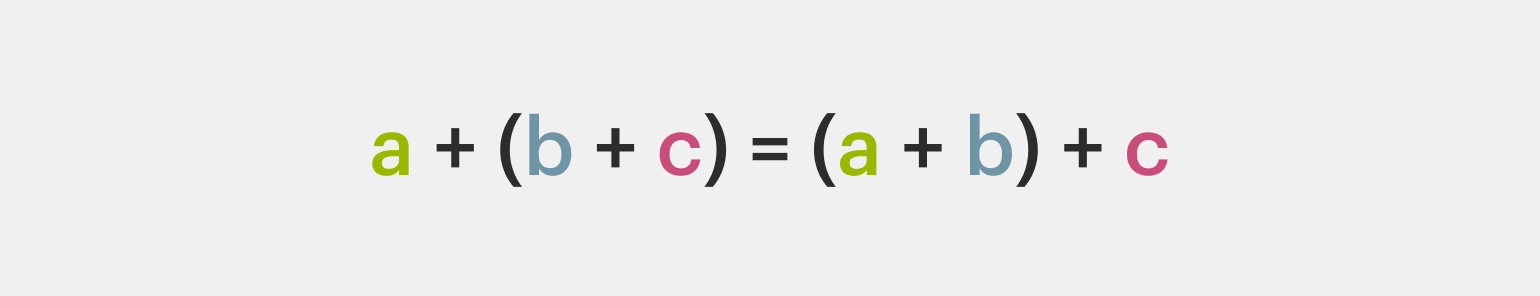
3️⃣ Ноль — нейтральный элемент. Сложение нуля с рациональным числом не изменит это число:

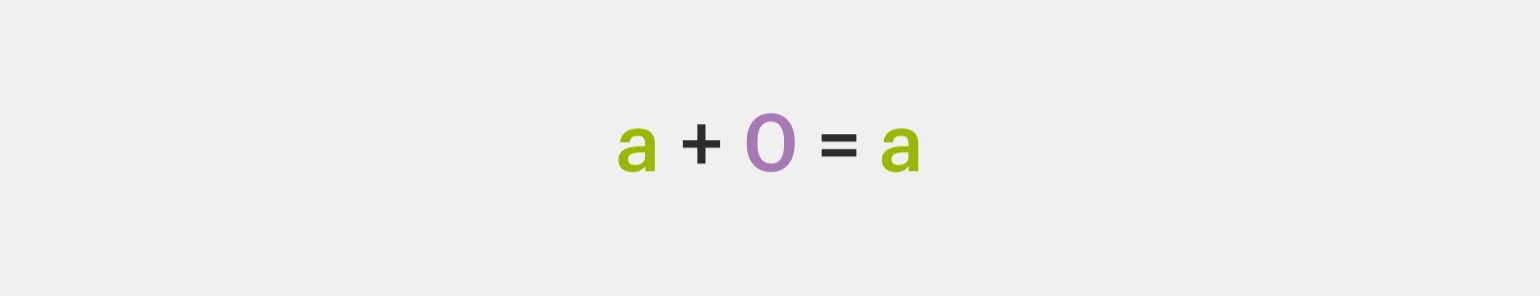
4️⃣ Наличие противоположного числа. У каждого рационального числа есть противоположное, а при их сложении мы получим 0:

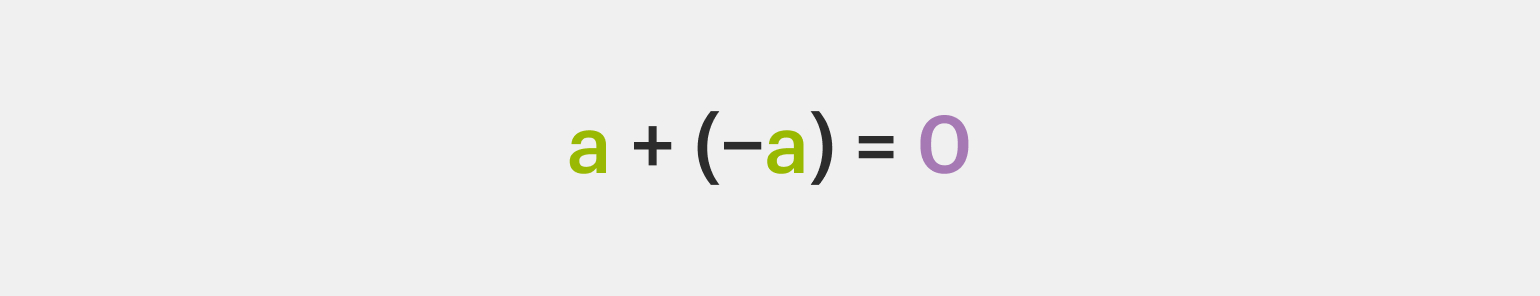
Чтобы лучше запомнить эти свойства, сохраните себе такую шпаргалку:

Свойства умножения с положительными множителями

Здесь всё практически идентично.

1️⃣ Переместительное свойство. От перемены мест множителей произведение не меняется:

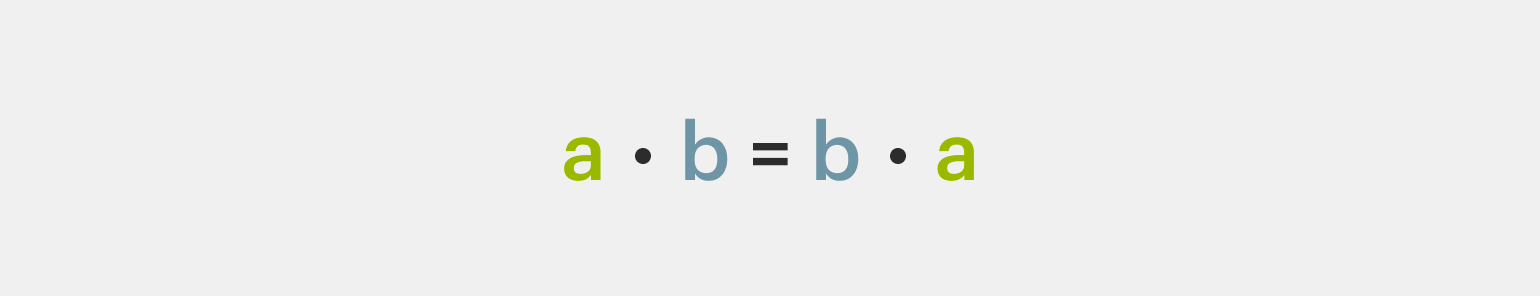
2️⃣ Сочетательное свойство. Чтобы умножить рациональное число на произведение двух чисел, нужно первое число умножить сначала на первый, а потом на второй множитель:

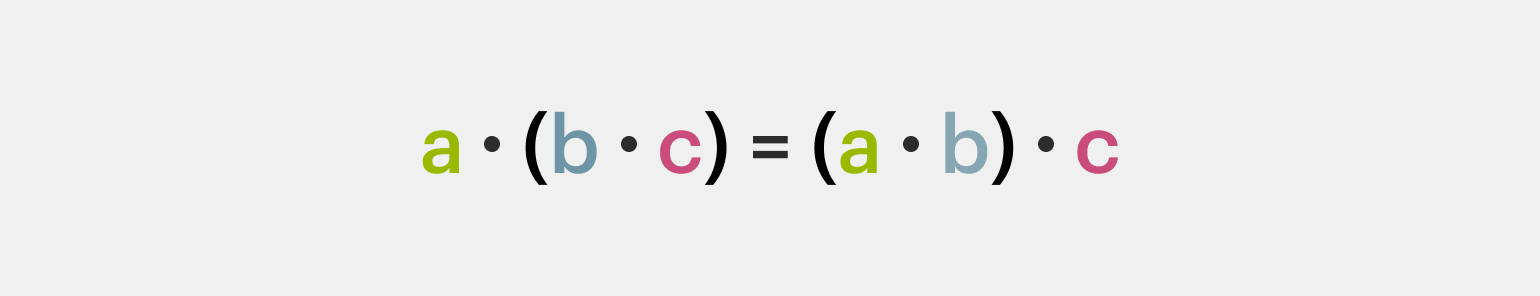
3️⃣ Свойство умножения на 1. При умножении рационального числа на 1 мы получим то же число:

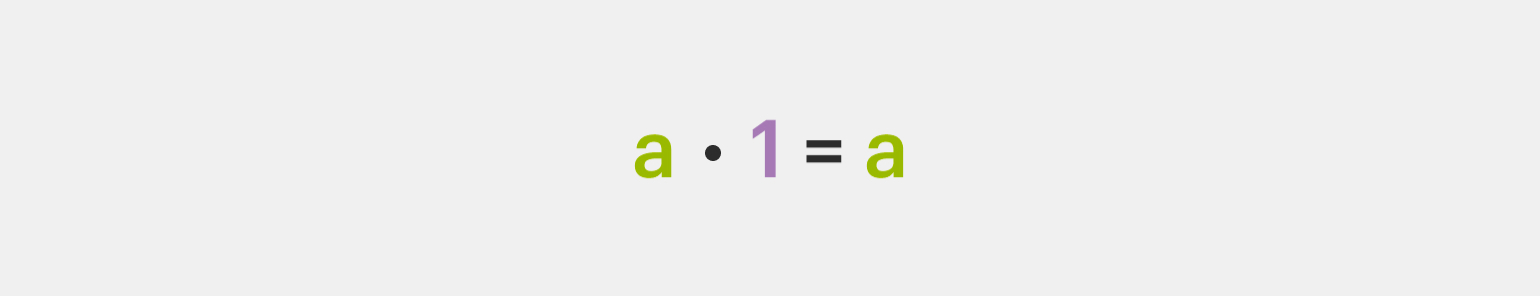
4️⃣ Свойство умножения на 0. При умножении рационального числа на 0 мы получим 0:

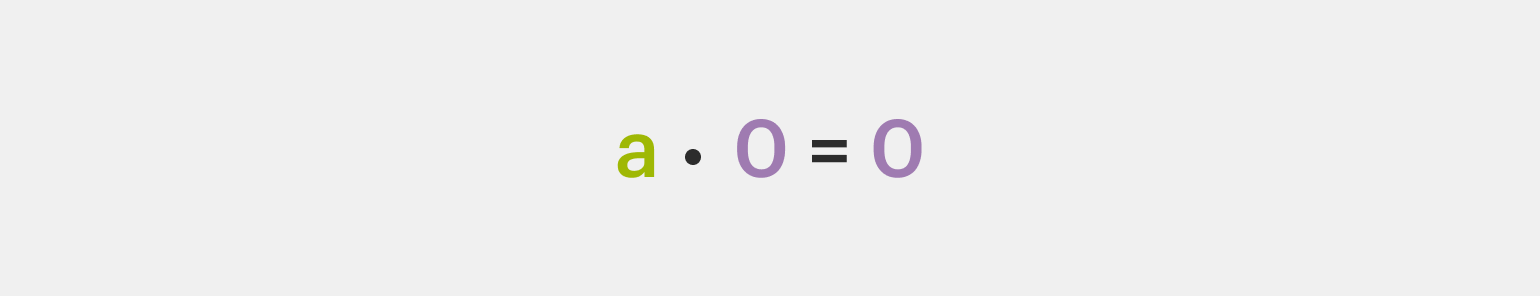
5️⃣ Свойство умножения на дробь. При умножении рационального числа на дробь, в числителе которой 1, а в знаменателе это же рациональное число, получится 1:

6️⃣ Распределительное свойство. При умножении суммы на рациональное число, можно умножить это число на каждое слагаемое отдельно, а потом эти значения сложить. Это же правило работает и с вычитанием:

Свойства умножения с отрицательными множителями

1️⃣Умножение чисел с разными знаками. Если есть хотя бы один отрицательный множитель, то всё произведение будет отрицательным (плюс на минус даёт минус, и минус на плюс даёт минус):

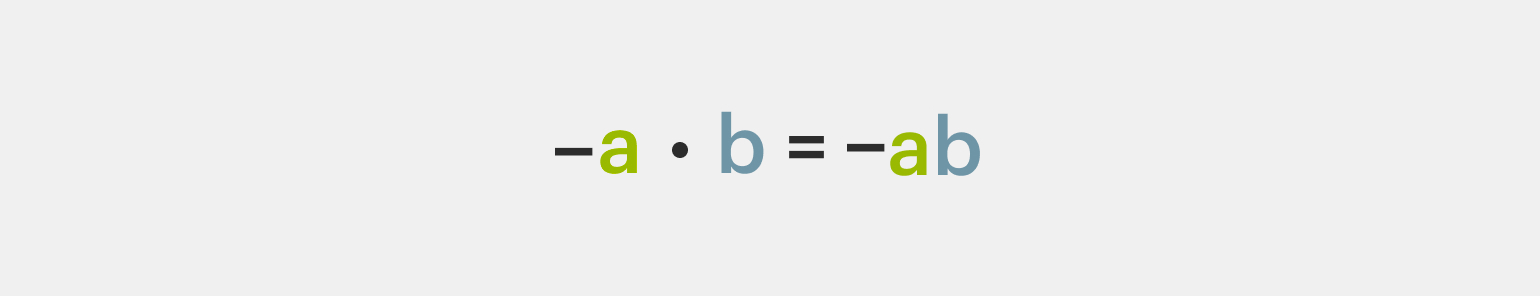
2️⃣Умножение отрицательных чисел: если мы умножаем оба отрицательных множителя, то произведение получится положительным (минус на минус даёт плюс):

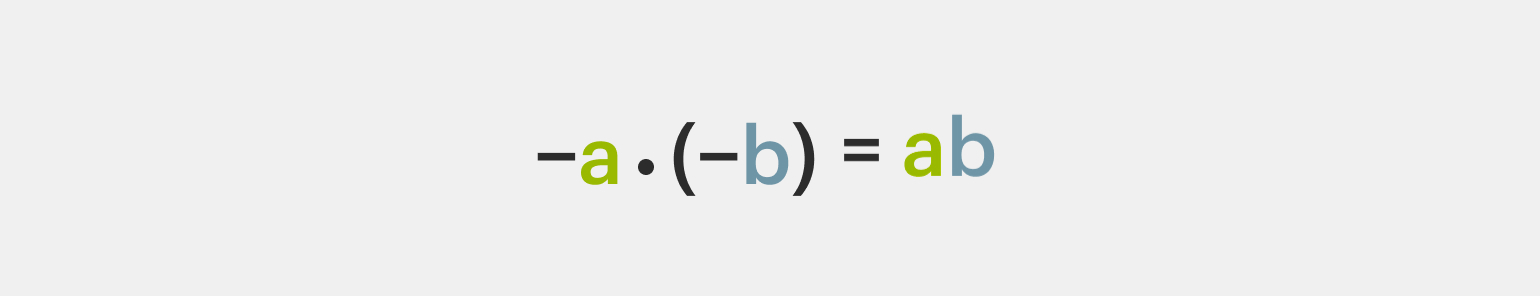
Свойства вычитания и деления

Свойства вычитания рациональных чисел можно описать по аналогии со свойствами сложения, главное — не запутаться с минусом. Например, a − b = −b + a:

А свойства деления рациональных чисел обратны свойствам умножения:

Рациональные числа в Python

Рассмотрим примеры рациональных чисел и их свойств на языке Python. В питоне есть специальный модуль fractions, который позволяет нам работать с рациональными числами, а в нём класс Fraction, являющийся реализацией дробного значения.

Ну что ж, за дело. Для начала импортируем класс Fraction из модуля fractions, чтобы мы могли им пользоваться:

from fractions import Fraction

Теперь разберём, как работает этот класс. При создании объекта Fraction в конструктор можно передать:

• два значения, где первое — это числитель, а второе — знаменатель (переменная a);
• дробное значение в виде строки (переменная b);
• вещественное значение (переменная c);
• другой Fraction, так как Fraction и является реализацией рационального дробного значения (переменная d).

a = Fraction(1, 2)
b = Fraction('1/2')
c = Fraction(0.5)
d = Fraction(a)

print(a, b, c, d)
print(float(a), float(b), float(c), float(d))
1/2 1/2 1/2 1/2
0.5 0.5 0.5 0.5

Видно, что значение переменных Fraction при выводе показывает дробный вид рационального числа 0,5, а во второй строке вывода при приведении значения ½ к float, получим его вещественное представление.

Поменяем значения переменных и пройдёмся по свойствам рациональных чисел, взяв отрицательную дробь -¾, дробь ⅔ (с бесконечным периодом) и целое число 10:

a = Fraction(-3, 4)
b = Fraction(2, 3)
c = Fraction(10)

Возьмём сочетательное свойство сложения и применим формулу (a + b) + c = a + (b + c), дабы убедиться, что значения будут равны, а также приведём вид дробей к float:

print((a + b) + c, '=', a + (b + c))
print(float((a + b) + c), '=', float(a + (b + c)))
119/12 = 119/12
9.916666666666666 = 9.916666666666666

Как можно заметить, значения одинаковые, а при выводе в вещественном виде у нас получается число с бесконечным периодом 6. А как мы уже говорили выше, такие числа также относятся к рациональным.

Проделаем ту же операцию по формуле распределительного свойства умножения:

print((a + b) * c, '=', a * c + b * c)
print(float((a + b) * c), '=', float(a * c + b * c))
-5/6 = -5/6
-0.8333333333333334 = -0.8333333333333334

Значения получились равные, но можно заметить, что при приведении к вещественному виду период рационального числа нарушается — 3 в конце заменяется на 4. Это происходит в силу особенностей вычислений в языке Python. Если мы на листе бумаги разделим 5 на 6, то получим 0,8333…, где 3 будет повторяться до бесконечности.

И напоследок разберём случай с делением рациональных чисел с использованием переместительного свойства. Для начала разделим a на b. Теперь поменяем операнды местами и посмотрим, что получится. Для этого умножаем a на дробь 1/b, подставив в качестве второго операнда класс Fraction, который и реализует эту дробь. Вуаля:

print(a / b, '=', a * Fraction(1, b))
print(float(a / b), '=', float(a * Fraction(1, b)))
-9/8 = -9/8
-1.125 = -1.125

Резюме: повторим изученное

Из этой статьи мы узнали, что такое рациональные числа, чем они отличаются от других видов чисел и какие у них есть свойства. Давайте пройдёмся по основным моментам, дабы закрепить знания.

• Рациональное число — это число, которое можно представить в виде дроби, где числитель — целое число, а знаменатель — натуральное.
• Рациональные числа — это все натуральные и целые числа, а также дроби: обыкновенные, конечные десятичные и бесконечные периодические.
• Бесконечные периодические дроби — это такие дроби, где есть повторяющаяся последовательность после запятой. Например, 1,16161616… Если дробь бесконечная, а такой последовательности нет, число называется иррациональным.
• У рациональных чисел есть математические свойства: переместительное, сочетательное, распределительное и так далее.
• С рациональными числами можно проводить любые математические операции, такие как сложение, вычитание, деление, умножение и другие.