Перестановки, сочетания и размещения: стартер-пак по комбинаторике для IT

Комбинаторика — это раздел математики, который изучает, сколько существует комбинаций между элементами множества. Например, между буквами алфавита, товарами в интернет-магазине или способами добраться из дома до университета.

Допустим, вы придумали пароль и хотите узнать, насколько сложно его взломать. Пароль состоит из восьми символов — цифр и букв латинского алфавита разного регистра. Подключаем комбинаторику, и вжух: выясняется, что при этих вводных существует аж 218 триллионов разных комбинаций пароля. Да, брутфорсерам придётся сильно постараться, чтобы подобрать нужную.

Возможности комбинаторики широко используются при построении алгоритмов в data science и в классическом программировании. Поиск оптимального маршрута в «Яндекс Картах», рекомендации товаров в интернет-магазинах, расчёт цепочек поставок — во всех этих алгоритмах присутствует незримая рука комбинаторики.

В этой статье мы изучим:

• основные понятия;
• сложение;
• умножение;
• перестановки;
• сочетания;
• размещения;
• выбор формулы;
• что запомнить.

Основные понятия

Для начала разберём несколько важных для понимания комбинаторики сущностей.

Множество — это набор элементов, которые мы перебираем. Например, в случае с паролем это были цифры и буквы латинского алфавита — всего 62 символа.

Выбор — это действие, при котором мы из множества достаём какие-то составляющие. Например, в случае с паролем можно выбрать символы i, C, 5, K, x, k, 0, w.

Расположение — это действие, при котором мы расставляем выбранные элементы в определённом порядке. Например, Cxi0kK5w или kxw0C5iK.

Факториал — это математическая функция, с помощью которой мы перемножаем все числа от 1 до какого-то числа. Факториал обозначается восклицательным знаком — !. Например, 5! = 1 * 2 * 3 * 4 * 5 = 120.

Читайте также:

Что такое факториал и как его вычислить

В зависимости от условий комбинаторной задачи применяются разные формулы. Некоторые задачи могут требовать только выбора, некоторые — только расположения, а некоторые — и выбора, и расположения. В одних задачах компоненты множества могут повторяться, в других — не могут.

Сложение

Сложение используется тогда, когда мы выбираем элемент из нескольких пересекающихся подмножеств.

Пример

Вы хотите скачать IDE для работы с кодом. У вас есть выбор из 7 платных программ и 8 бесплатных. Следовательно, вы можете выбрать программу 15 разными способами.

Умножение

Умножение используется тогда, когда вы выбираете элементы последовательно, друг за другом.

Пример: вы хотите выучить два иностранных языка из десяти самых распространённых. Сколько разных комбинаций языков вы можете выучить?

Решение: сначала мы берём один из 10 языков, а потом — один из оставшихся 9. По правилу умножения получается 9 * 10 = 90 разных комбинаций из двух языков.

Перестановка

Перестановка — это способ последовательно расположить составляющие множества. Например, 123, 312 и 213 — это перестановки трёх чисел: 1, 2 и 3.

Чтобы найти общее количество возможных перестановок, используют две формулы: для случаев с повторяющимися компонентами и без них. Давайте рассмотрим оба.

Перестановка без повторяющихся элементов

Если во множестве ни один элемент не повторяется, то используется следующая формула:

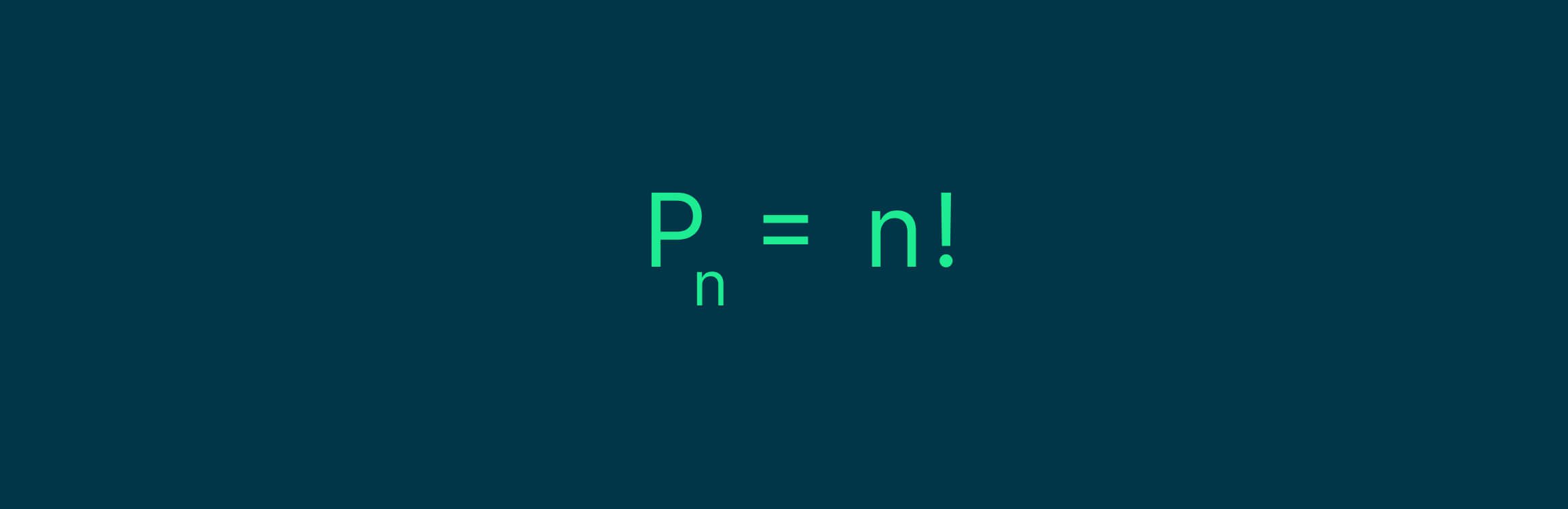
Пример: сколько перестановок символов можно составить из шести букв — q, w, e, r, t, y?

Решение: чтобы найти количество перестановок, нам нужно посчитать факториал числа 6 — то есть общего количества букв в наборе. Подставляем в формулу:

Перестановка с повторяющимися элементами

Если хотя бы один элемент во множестве повторяется, то используется следующая формула:

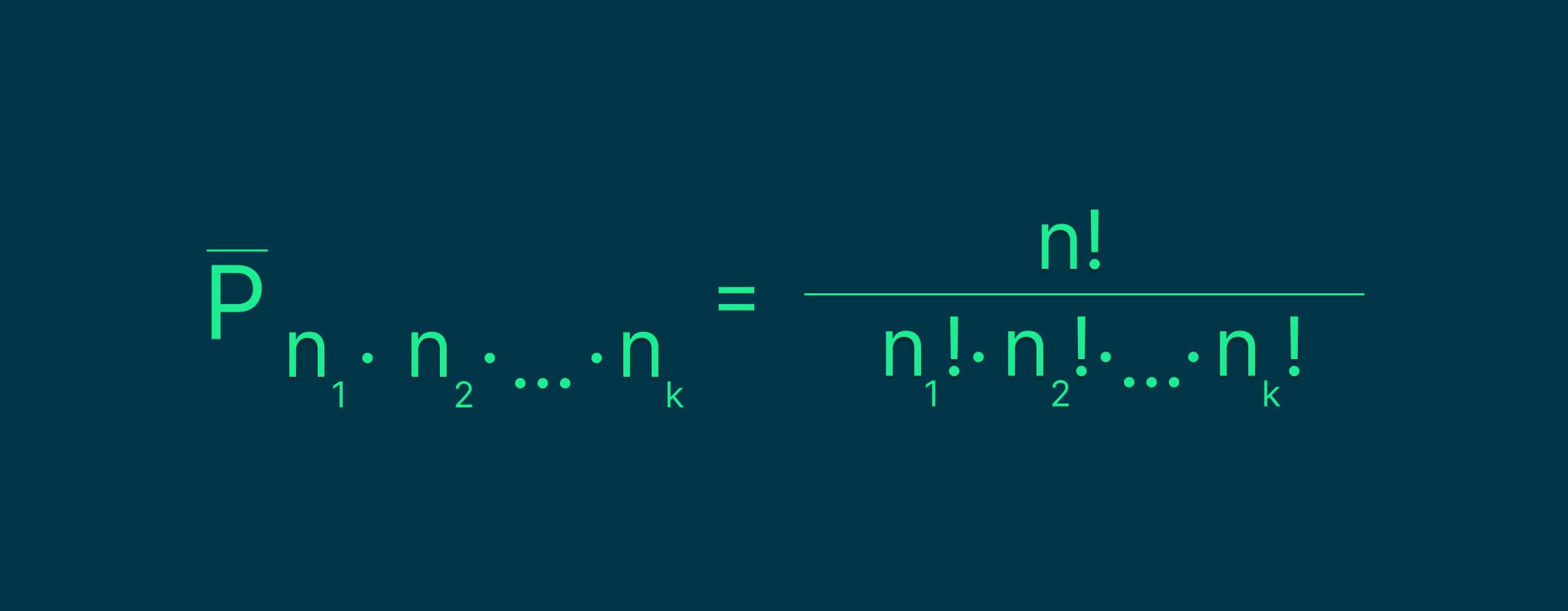
Формула выглядит довольно негуманно, поэтому объясним, в чём здесь логика. Сначала мы находим, сколько перестановок было бы, если бы все компоненты множества были разными. Потом мы делим это число на то, сколько раз можно переставить повторяющиеся элементы между собой. Это нужно, чтобы не считать одинаковые перестановки несколько раз. Дальше мы посмотрим на пример, чтобы лучше разобраться.

Пример. Допустим, у нас есть набор из восьми букв: p, a, s, s, w, o, r, d. Сколько всего перестановок символов можно составить из этих букв?

Решение. Видим, что буква s в этом наборе повторяется дважды. Значит, n = 8 и n₁ = 2. Подставляем эти значения в формулу и получаем:

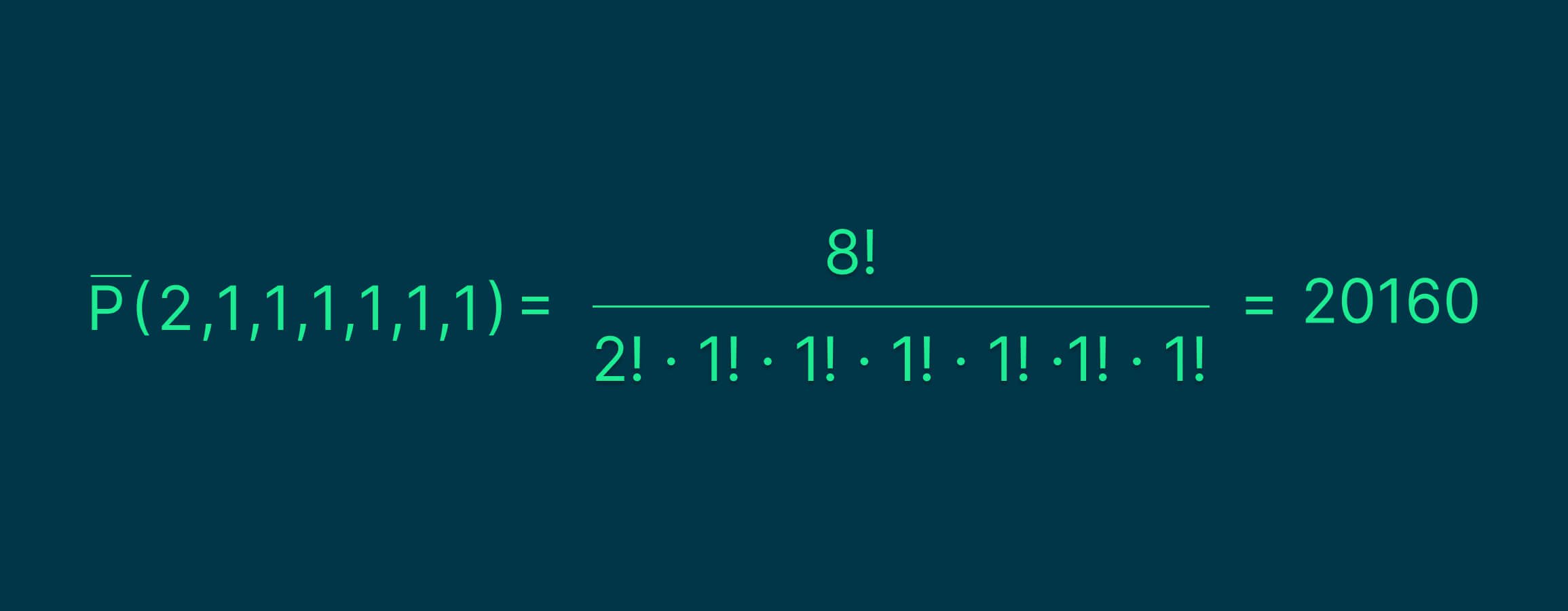
Сочетание

Сочетание — это неупорядоченный набор элементов, взятых из множества. В сочетании используется только выбор, расположение не используется.

Операция сочетания помогает выяснить, сколькими способами можно выбрать k элементов из множества n.

Сочетание без повторяющихся элементов

Если во множестве n ни один элемент не повторяется, то используется следующая формула:

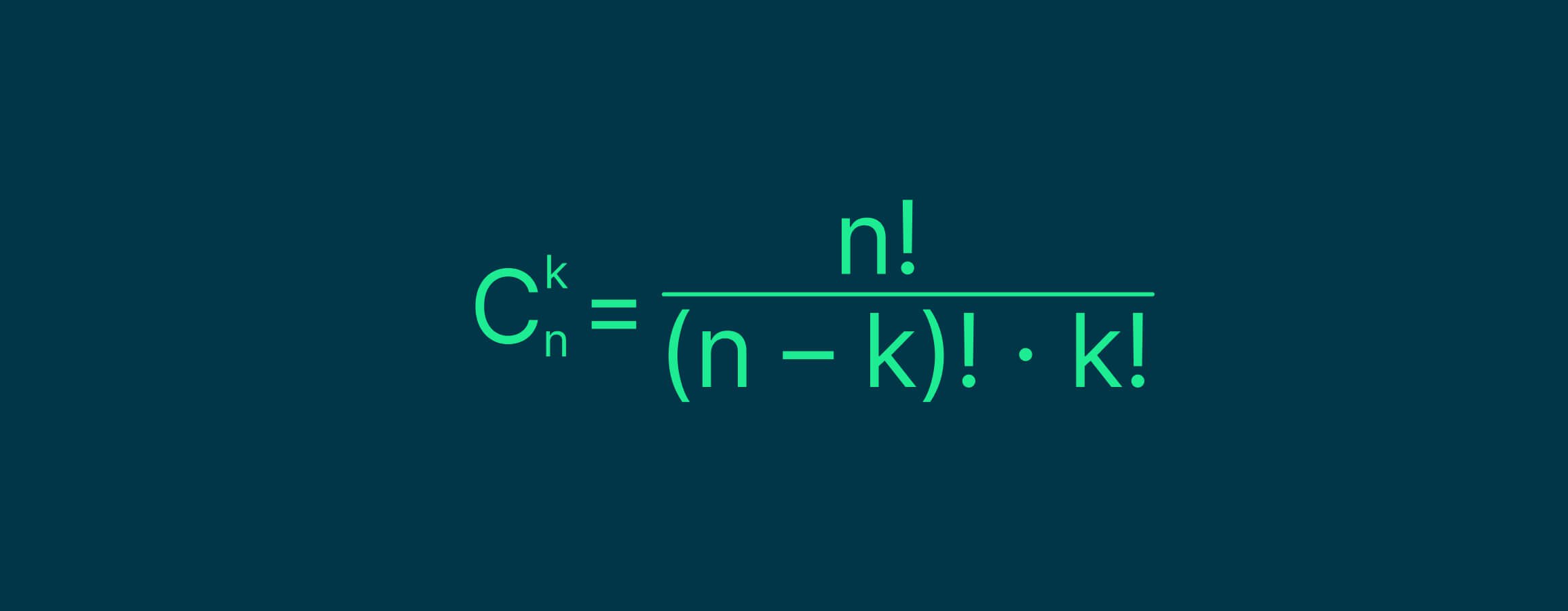
Пример. Студент выбирает 3 языка программирования, которые он хочет изучить. Ему предлагают 50 вариантов. Сколько всего сочетаний языков он может выучить?

Решение. В этом случае студент выбирает k = 3 языков из n = 50 вариантов. Подставляем эти значения в формулу и получаем:

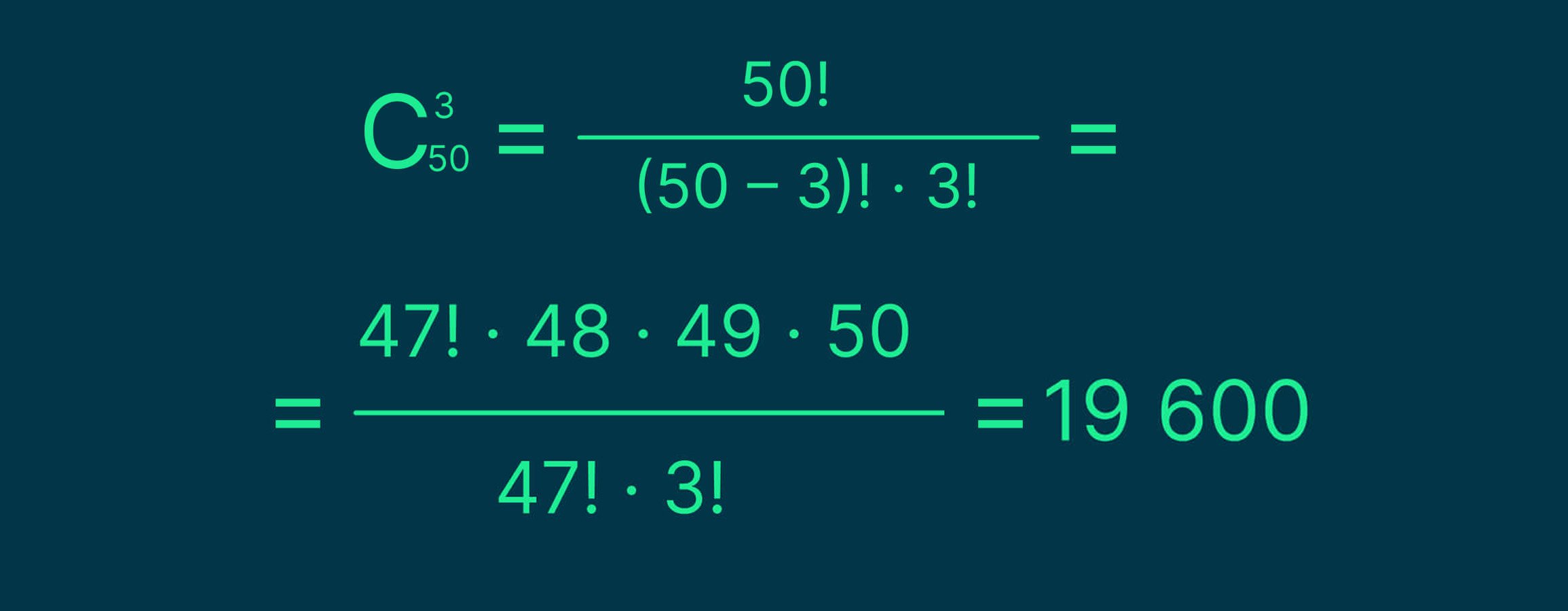
Сочетание с повторяющимися элементами

Если во множестве n какой-то элемент повторяется, то используется следующая формула:

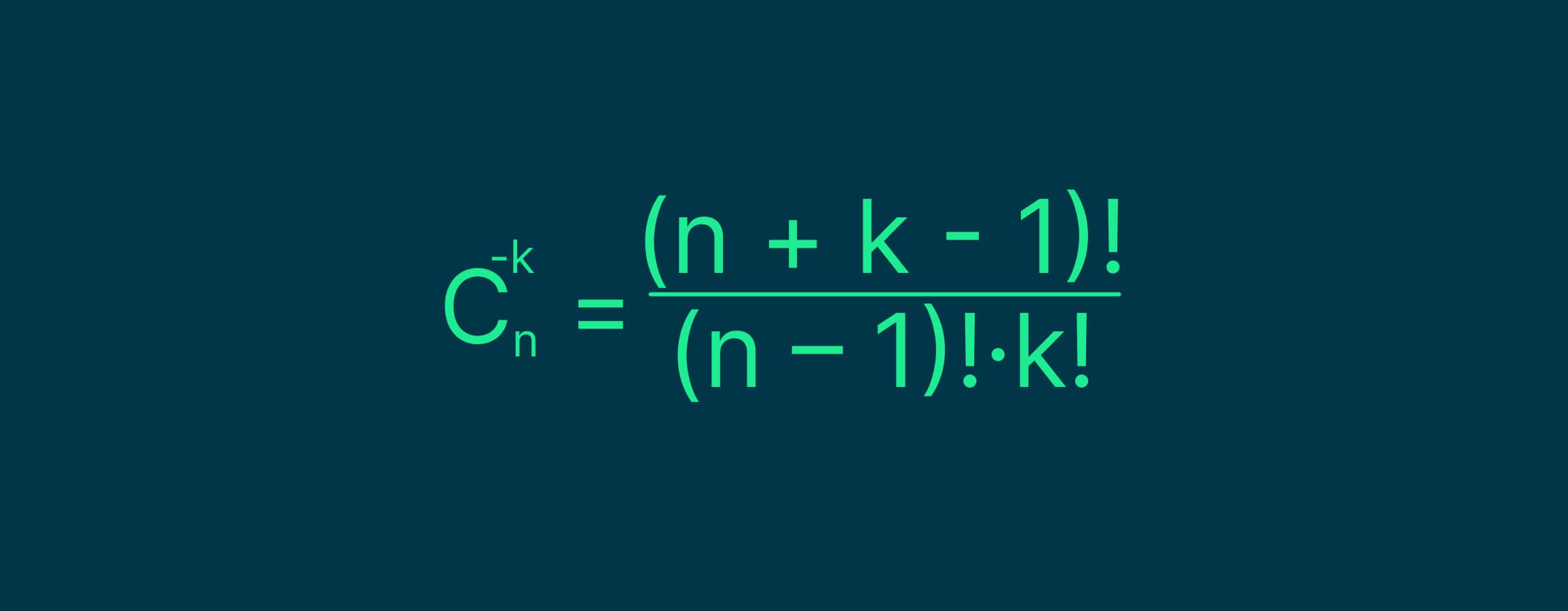
Пример. Школьник собирает гербарий из 7 листьев для урока по окружающему миру. Рядом с его домом растут клён, дуб и берёза. Сколько сочетаний листьев разных деревьев он может собрать в гербарии?

Решение. Так как в нашей задаче листьев больше, чем деревьев, воспользуемся формулой сочетаний с повторениями. Подставляем 3 вместо n и 7 вместо k — и получаем такое выражение:

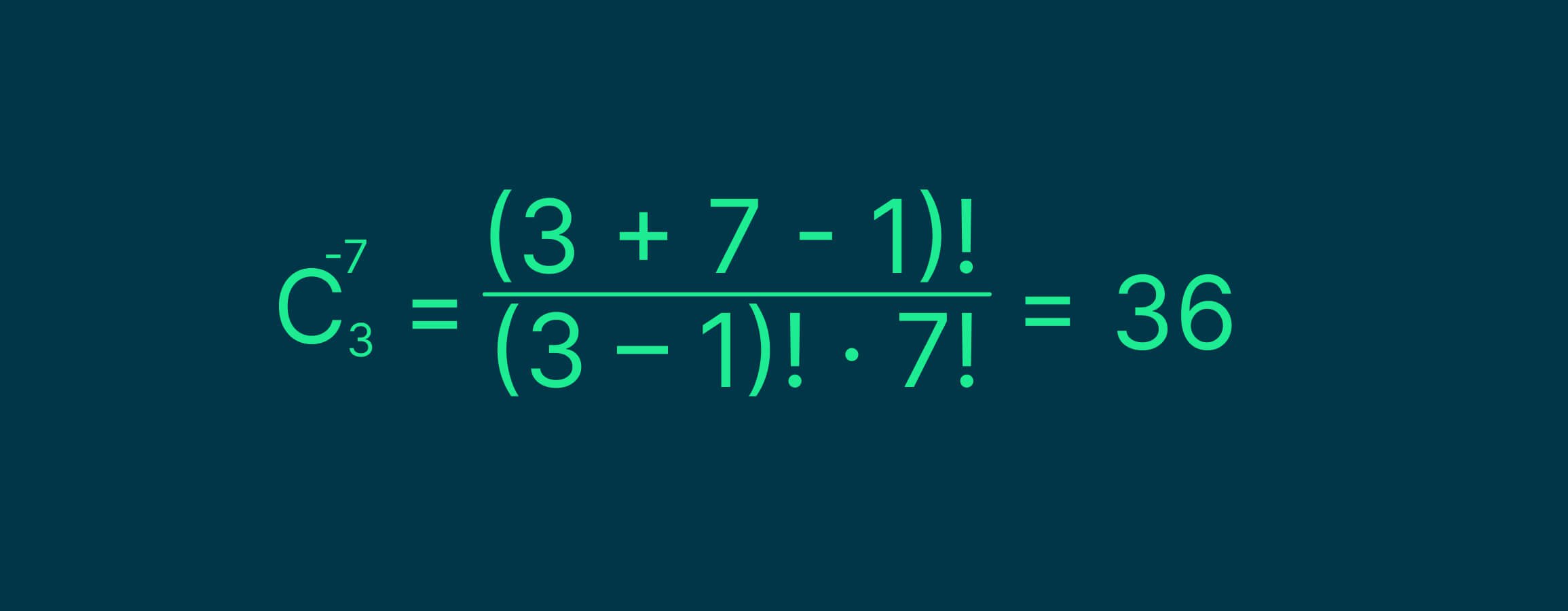
Получается, у школьника есть 36 возможных комбинаций разных листьев. А теперь представьте, что учитель дал задание не просто выбрать листья, а расположить их в определённом порядке на листе ватмана — например, клён-дуб-клён-берёза-клён-дуб-клён. Сколько всего таких наборов можно составить? В этом случае важен порядок листьев и один и тот же набор может давать разные расположения. Чтобы решить задачу в таком случае, нужно использовать другую операцию комбинаторики — размещение.

Размещение

Размещение — это способ выбрать и упорядочить элементы из множества. В отличие от операции сочетания, при размещении важен порядок составляющих множества.

Вопрос размещения: сколько упорядоченных наборов можно сделать из k элементов, выбранных из n?

Размещение без повторяющихся элементов

Если во множестве n ни один элемент не повторяется, то используется следующая формула:

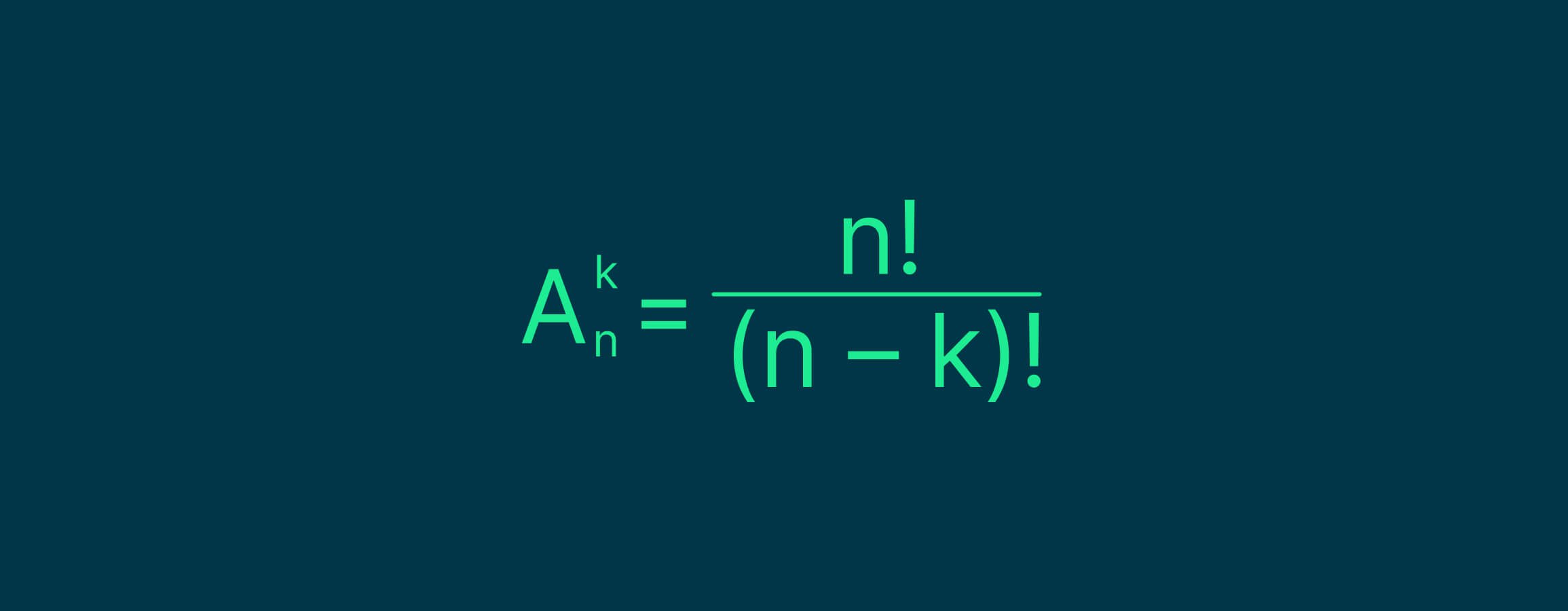
Пример. В лототроне находится 90 шаров с номерами от 10 до 99. Ведущий последовательно достаёт три шара и кладёт их рядом так, чтобы получилось шестизначное число. Сколько вариантов шестизначных чисел может получиться?

Решение. Ведущий выбирает и упорядочивает 3 шара из 90. Подставляем числа в формулу выше и смотрим на результат:

Размещение с повторяющимися элементами

Если во множестве n один и тот же элемент можно взять несколько раз, то используется следующая формула:

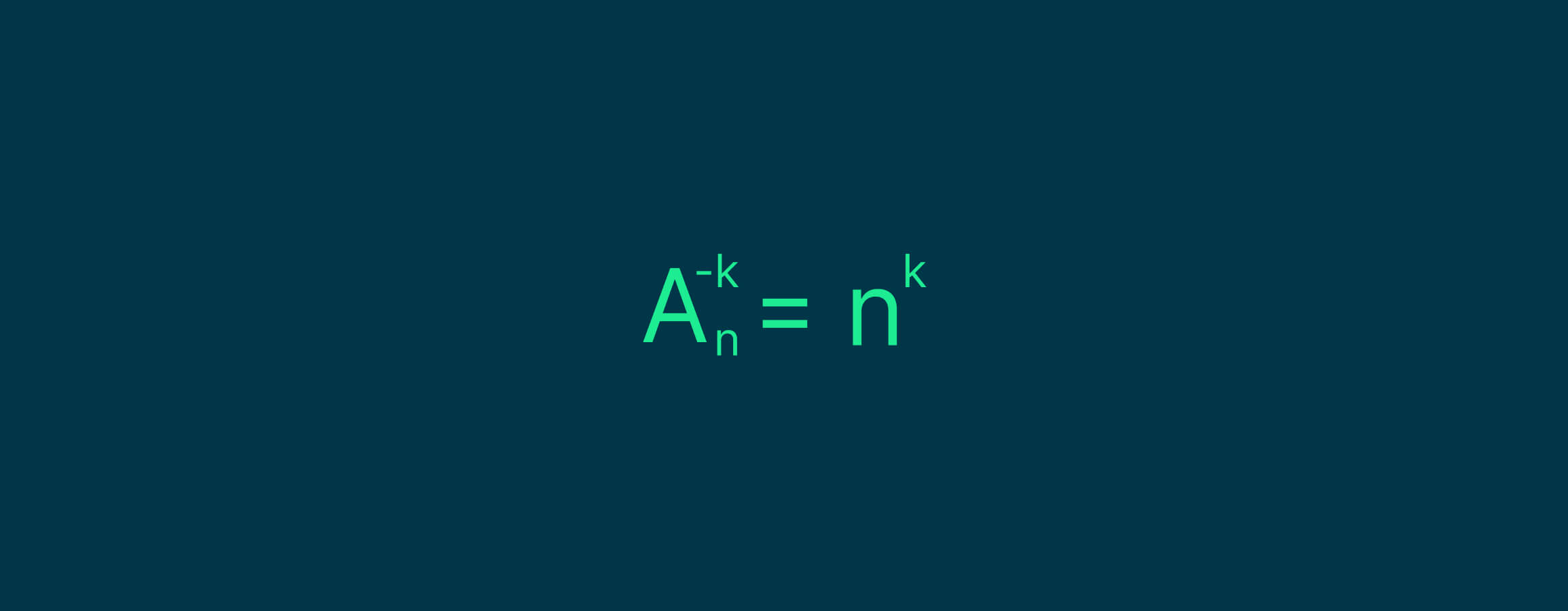
Пример. В начале статьи мы писали о восьмисимвольном пароле, состоящем из латинских букв (заглавных и строчных) и цифр от нуля до девяти. Любой символ может использоваться сколько угодно раз. Сколько всего таких паролей можно составить?

Решение. Букв в латинском алфавите 26, следовательно, в пароле можно использовать 26 * 2 = 52 буквенных символа (26 для заглавных и 26 для строчных). Цифр от нуля до девяти — 10. В итоге получаем множество из 62 составляющие.

Вуаля! Если держать под рукой калькулятор и формулы комбинаторики, задача уже не кажется такой сложной, правда? Но это только если мы сразу определимся, какую формулу использовать, — а это не всегда можно сделать быстро. К счастью, у математиков и на этот случай есть лайфхак.

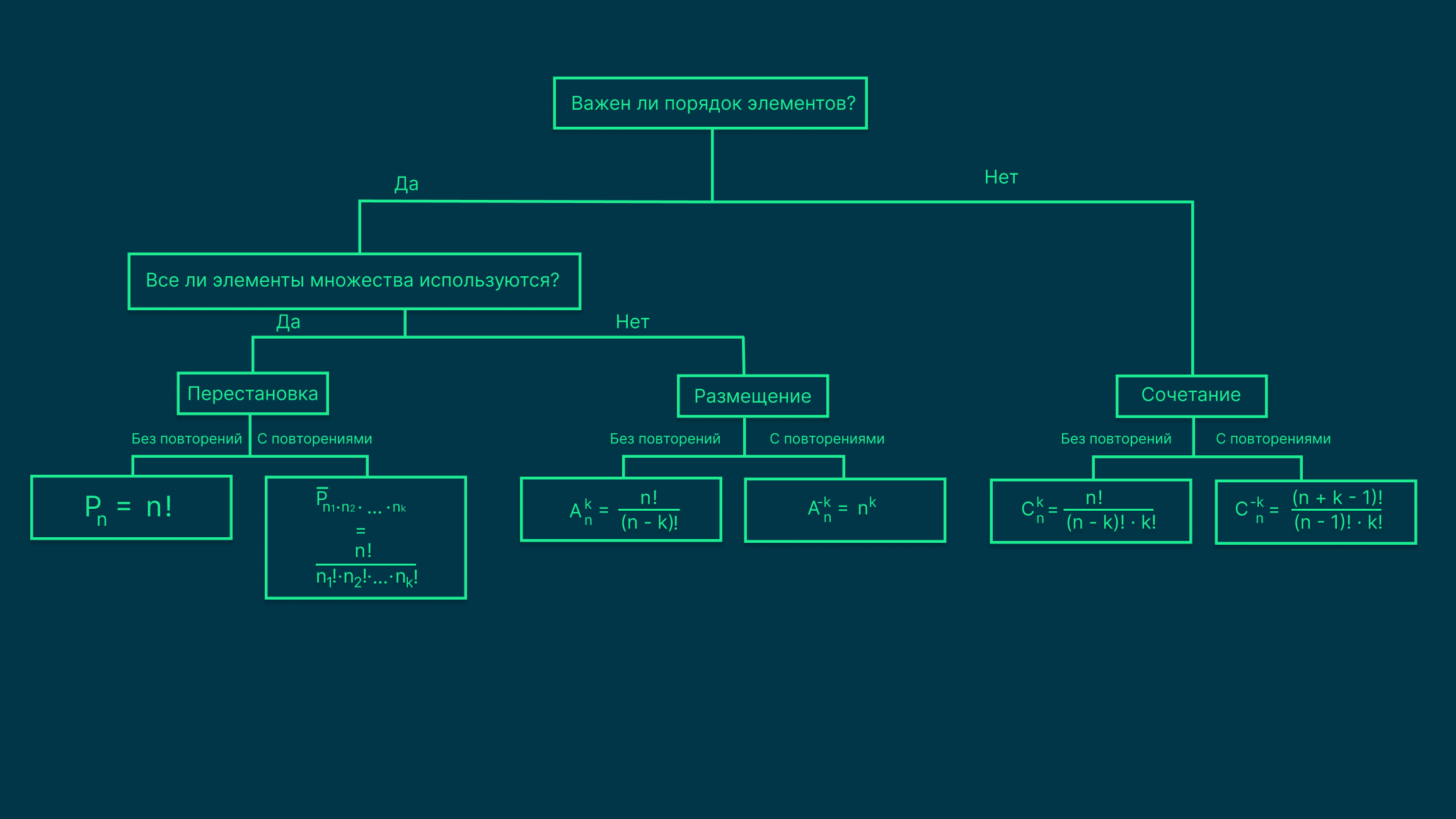
Как выбрать нужную формулу

Чтобы быстро решить, какую из формул комбинаторики использовать, можно воспользоваться следующей схемой:

Что запомнить

Комбинаторика — это раздел математики, в котором изучается выбор и размещение элементов, взятых из некоторого множества.

В комбинаторике три базовые конфигурации:

• Перестановка — это способ последовательно расположить элементы во множестве.
• Сочетание — это набор элементов, который можно выбрать из множества без учёта порядка.
• Размещение — это упорядоченный набор элементов, который можно выбрать из множества.

В зависимости от того, повторяются или нет составляющие множества, для подсчёта всех комбинаций используются разные формулы.