Машина Тьюринга — что это: роскошь или средство вычисления?
Рассказываем о концепции, которая легла в основу всех современных компьютеров.


Любой, кто интересуется информатикой, компьютерами и IT, рано или поздно встретит термин «машина Тьюринга». Понять, что это, с помощью соответствующей страницы в «Википедии» категорически невозможно, даже не пытайтесь. Поэтому мы решили справиться сами — и вам рассказать.
Всё, что нужно знать о машине Тьюринга
- Зачем она нужна
- Как устроена
- Принцип работы
- Роль в истории
- Полнота по Тьюрингу
- Примеры реализации
- При чём тут грибы?
Зачем она нужна
В XVII веке знаменитый математик Готфрид Лейбниц мечтал о создании машины, которая могла бы определять истинность математических утверждений.
Три века спустя другой выдающийся математик, Давид Гильберт, мечтая о том же, сформулировал задачу. Он хотел найти алгоритм, который принимал бы в качестве входных данных описание любой проблемы разрешимости. А после конечного числа шагов останавливался бы и выдавал один из двух ответов: «истина» или «ложь».

Фото: Wikimedia Commons
Чуть позже, в 1930-е годы, к этому же вопросу обратился третий, не менее знаменитый, математик Макс Ньюман. Он преподавал в Кембридже, был криптоаналитиком и одним из создателей Colossus — самого большого компьютера тех времён.
«Есть ли конкретный метод или механический процесс, который можно применить к математическому утверждению и он ответит, доказуемо ли это утверждение?»
Из лекций Макса Ньюмана,
цитата по книге Чарльза Петцольда «Читаем Тьюринга»

Фото: Wikimedia Commons
Среди студентов Ньюмана был пока ещё никому не известный математик Алан Тьюринг. Валяясь на лугах Гранчестера, где любили отдыхать тогдашние хипстеры, он размышлял над словами Ньюмана. Итогом этих раздумий стала статья On Computable Numbers, with an Application to the Entscheidungsproblem
«Я предполагаю, что Тьюринг с самого начала своей работы ставил перед собой цель доказать неразрешимость Entscheidungsproblem. Он сказал мне, что „главная идея“ статьи пришла к нему, когда он лежал на лугах Гранчестера летом 1935 года. Главной идеей мог быть либо его анализ вычислений, либо осознание существования универсальной машины, а значит, и диагональный аргумент для доказательства неразрешимости».
Из воспоминаний ученика и друга Тьюринга Робина Ганди,
цитата по книге The Universal Turing Machine. A Half-Century Survey (1995), Rolf Herken

Фото: Christie’s
Именно в этой статье, опубликованной в 1936 году, была впервые описана машина Тьюринга. Правда, сам автор использовал понятие «вычислительная машина» (computing machine); в честь него модель назовут чуть позже.

Фото: Wikimedia Commons
Тьюринг пошёл не по привычному пути формул и доказательств, а начал с описания машины, которая совершает несколько простых операций. Хотя компьютеров тогда не было, если не считать прообразов вычислительных машин, созданных Чарльзом Бэббиджем и Вэниваром Бушем.
Что такое машина Тьюринга и как она устроена
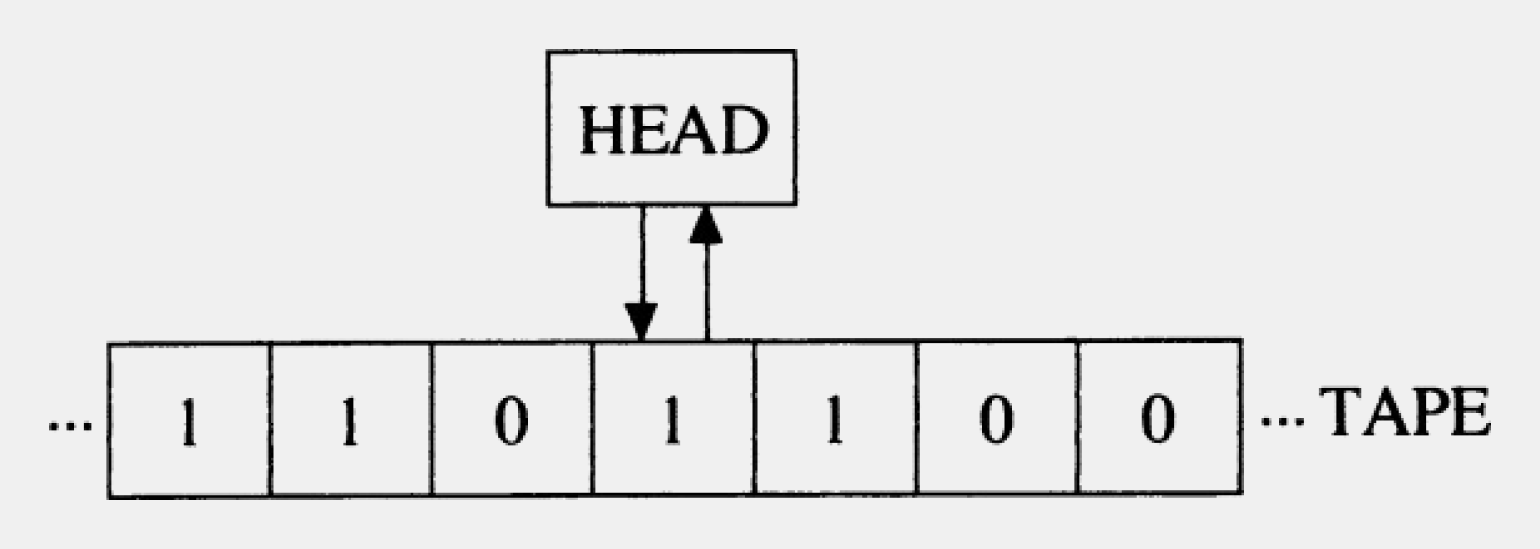
Машина Тьюринга — это абстрактная вычислительная машина, мысленный эксперимент для решения проблемы математической логики. Она состоит из трёх элементов:
- бесконечной ленты с ячейками;
- автомата или головки для чтения и записи;
- программы.
«Машина снабжена „лентой“ (аналог бумаги), проходящей через неё и разделённой на участки (называемые квадратами), каждый из которых может содержать символ».
А. Тьюринг,
«О вычислительных числах, с приложением к проблеме принятия решений»
Изображение: Computational Error and Complexity in Science and Engineering / V. Lakshmikantham, S. K. Sen / Mathematics in Science and Engineering, 2005
Принцип работы машины Тьюринга
Машина работает следующим образом: головка может прочитать содержимое конкретной ячейки, стереть, перезаписать и/или передвинуться на ячейку влево или вправо и повторить считывание/запись.
«В некоторых конфигурациях, в которых ячейка пуста (то есть не содержит символа), машина записывает новый символ в эту ячейку: в других конфигурациях она стирает символ. Машина может также поменять ячейку, но только путём смещения его на одно место вправо или влево».
А. Тьюринг,
«О вычислительных числах, с приложением к проблеме принятия решений»
Действия головки определяются программой. Она записывается в виде таблицы, где есть внешний и внутренний алфавиты и таблица переходов между ними. Внешний алфавит — это конечное множество, элементы которого называются буквами или символами. Внутренний алфавит — это конечное множество состояний головки. Таблица переходов описывает поведение головки. Команда, которую должна выполнить головка, определяется пересечением внешнего и внутреннего алфавитов в таблице.
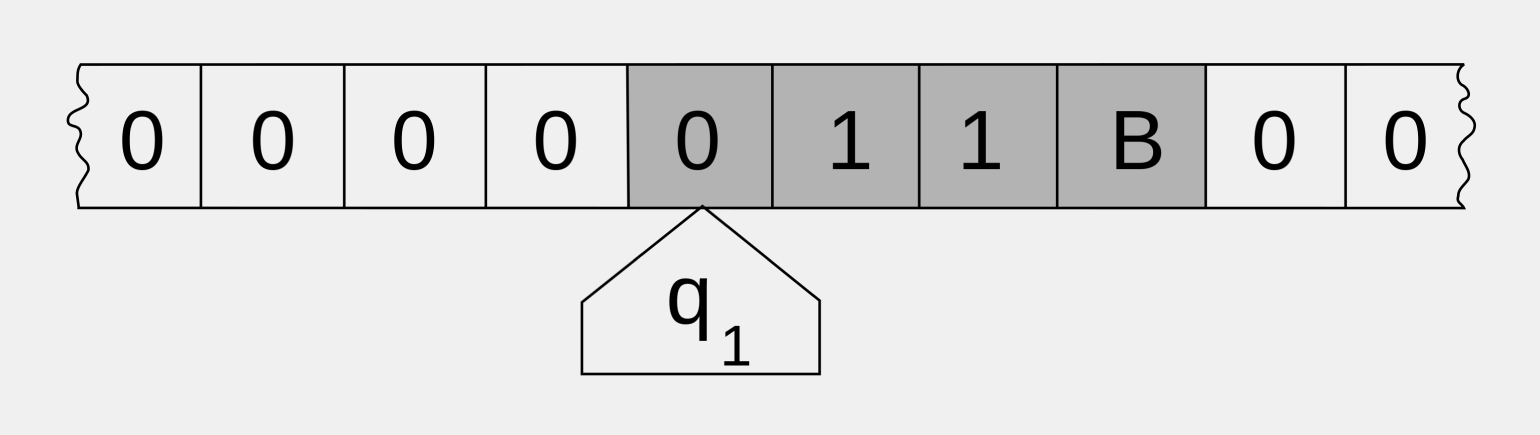
На рисунке выше изображена лента, входная информация (11В) расположена так, что в каждой клетке по одному символу. До и после неё — нулевые ячейки. Исходное состояние головки — q1. Это состояние запускает работу машины. Головка может сдвинуться влево и вместо 0 записать цифру или букву. Также она может сдвинуться вправо и перезаписать 1 другой цифрой или буквой. Или передвинуться ещё на ячейку влево/вправо без перезаписи.
Головка может также остаться на месте и ничего не делать. Выполнение операций прекращается после того, как головка считывает пассивное состояние — q0.
В чём же важность этой, на первый взгляд, нехитрой конструкции?
Роль в истории
Историческое значение машины Тьюринга в том, что это первая математическая модель универсальных вычислений. Другими словами, всё, что можно вычислить, описывается как машина Тьюринга. Это не единственная модель вычислений, но, пожалуй, самая известная и популярная. И ещё это описание работы компьютера, которое Тьюринг дал до появления компьютеров.
«Его машины предлагали мост, связь между абстрактными символами и физическим миром».
Эндрю Ходжес,
«Алан Тьюринг: Энигма»
Также новаторство Тьюринга было в том, что его машина использовала двоичную систему во времена, когда преобладала десятичная. Привычные для нас двоичные числа для большинства читателей в 1936 году были не столь знакомы. Так, компьютер ENIAC (1943–1945) использовал десятичную систему. А слово «бит» (сокращение от binary digit, «двоичная цифра») появилось в публикациях только в 1948 году.
«Если автоматическая машина печатает два вида символов, первый из которых (называемый цифрами) состоит исключительно из 0 и 1 (остальные называются символами второго вида), то машина будет называться вычислительной».
А. Тьюринг,
«О вычислительных числах, с приложением к проблеме принятия решений»
Важность работы Тьюринга была ещё и в том, что он описал универсальный компьютер «общего назначения». Это революционная концепция. В то время компьютеры разрабатывались специально для определённых видов работ. Например, Вэнивар Буш со студентами в 1920-е годы придумал аналоговый компьютер, известный как дифференциальный анализатор. Он решал обыкновенные дифференциальные уравнения — и это было всё, что он делал.
«Не нужно разрабатывать разные машины для выполнения различных вычислительных процессов. Все они могут быть выполнены с помощью одного цифрового компьютера, соответствующим образом запрограммированного для каждого случая».
А.Тьюринг,
«Вычислительная техника и интеллект»
Никто не доказал, что существует более эффективная модель вычислений, чем машина Тьюринга. Она отвечает на вопрос, какие минимальные условия нам нужны для выполнения любого вычисления. Ответ на этот вопрос показывает нам ограничения компьютеров. Если мы можем произвести определённое вычисление на машине Тьюринга, значит, его можно сделать на любом другом компьютере. Это называется «полнота по Тьюрингу».
Полнота по Тьюрингу
Полнота по Тьюрингу — одно из базовых понятий в информатике. Полный по Тьюрингу язык программирования или компьютер способен имитировать машину Тьюринга. Он теоретически может выразить все задачи, решаемые компьютерами; почти все языки программирования Тьюринг-полные, если не обращать внимания на ограничения памяти.
Другими словами, можно написать на Java или C++ программу, которая будет действовать как машина Тьюринга. «Полными» также являются и HTML5, и CSS3. А вот SQL не полный — на нём пишутся в основном запросы к базе данных, а не полноценные программы.
Примеры реализации
Несмотря на то что данная разработка — это мысленный эксперимент, нашлись энтузиасты, которые попытались сконструировать её физический прототип.
Пожалуй, наиболее впечатляющую модель воспроизвел Ричард Ридел. У него ушло на её создание шесть месяцев.

Фото: Wikimedia Commons
Другие умельцы реализовали машину Тьюринга в Excel:
При чём тут грибы?
Несмотря на то что машина Тьюринга была придумана почти 100 лет назад, эта концепция не только не устарела, но и используется сейчас. Робототехник Джошуа Бонгард и биолог Майкл Левин в своих работах предлагают уйти от узкого понимания компьютеров и рассматривать живые организмы тоже как вычислительные машины.
«Это определение включает широкий спектр акторов, которые не выглядят как компьютеры, например стая крабов, грибы, жидкости и даже алгоритмы внутри других компьютеров».
Джошуа Бонгард и Майкл Левин,
«Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины»
И для того, чтобы определить, можно ли причислить этих крабов к компьютерам, они рассматривают их как машину Тьюринга. Правда, здесь у учёных возникают сложности, потому что в случае с грибами или жидкостями сложно определить, где лента, где считывающая головка, а где программа.
«Если даже система выглядит как машина Тьюринга, сложно выделить её отдельные компоненты, такие как лента или считывающая/записывающая головка».
Джошуа Бонгард и Майкл Левин,
«Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины»
Кроме того, биологические системы эволюционируют и меняются со временем, что также усложняет применение к ним жёстких математических определений.
«Такое поведение не только затрудняет постановку вопроса: „Это компьютер?“ — но вообще затрудняет любые попытки определить момент, когда система становится компьютером».
Джошуа Бонгард и Майкл Левин,
«Здесь много места: биологические системы как эволюционировавшие, перегруженные, многомасштабные машины»
Но ничего лучше машины Тьюринга, похоже, не придумали, поэтому Бонгарду и Левину придётся найти, где у крабов лента, а где считывающая головка.










