Лотфи Заде и его нечёткая логика
Рассказываем про открытие, которое имеет такую же важность в IT, как и общая теория относительности Эйнштейна в физике.


Сегодня, увидев шильдик «Fuzzy Logic» на только что купленном холодильнике, стиральной машинке или в системе управления автомобильным двигателем, мало кто удивится. А продвинутые пользователи даже обрадуются. Ещё бы: ведь это значит, что холодильник умеет регулировать мощность морозилки в зависимости от загрузки. Точно так же машинка будет сама выбирать режим стирки с учётом материала и загрязнённости белья, а двигатель не подведёт даже в самых экстремальных условиях.
Удивительно, но ещё полвека назад нечёткая логика, лежащая в основе всех этих замечательных технологий, не вызывала никакого энтузиазма даже у профессионалов. Многие математики и айтишники относились к ней скептически, а её автор Лотфи Заде при первой публикации даже всерьёз рисковал академической карьерой.
Впрочем, давайте познакомимся с нашим героем и его идеями подробнее. Тем более что биография у него была довольно самобытной с самого начала.
Одиссея инженера Лотфи Заде
Лотфи Заде родился в 1921 году в селе Новханы, в 20 километрах от Баку. Его отец был журналистом из Ирана. Мать, врач по образованию, бежала из Одессы из-за погромов 1905 года.
Ещё в детстве у мальчика проявились большие способности к математике, любовь к точным наукам и инженерному делу. Получив начальное образование в русской школе в Баку, в 1931 году Заде вместе с семьёй переехал на родину отца. Здесь будущий учёный окончил Американский колледж в Тегеране, а затем — электротехнический факультет университета.
После получения диплома организовал вместе с отцом бизнес по поставкам оборудования для американских войск — Вторая мировая война к тому времени была в самом разгаре. В 1943 году Лотфи принял решение переехать в США.
Он в совершенстве знал четыре языка: азербайджанский, русский, фарси и английский. Это во многом сформировало его жизненное и научное мировоззрение. В одном из интервью он описал себя как «американца, математически ориентированного инженера-электрика иранского происхождения, родившегося в России».

«Вопрос не в том, американец я, русский, иранец, азербайджанец или кто-то ещё. Меня сформировали все эти люди и культуры, и я чувствую себя вполне комфортно среди них».
Лотфи Заде
(цитата: Azerbaijan International)
Оффер от Винера
Приехав в Америку, Заде поступил в Массачусетский технологический институт (MIT) на специальность «инженер-электрик». По окончании учёбы он устроился в Колумбийский университет в Нью-Йорке.
«В 1947 году мои родители тоже приехали в Америку и поселились в Нью-Йорке, поэтому я пошёл работать инженером в Колумбийский университет. Мне хотелось быть ближе к родителям, помогать им».
Лотфи Заде
(цитата: Visions of Azerbaijan)
Здесь же началась его академическая карьера. Сначала Лотфи стал простым преподавателем, затем защитил диссертацию и в течение 10 лет дорос до звания профессора.
В 1957 году научными публикациями перспективного учёного заинтересовался легендарный Норберт Винер, основоположник кибернетики и теории искусственного интеллекта.
«В те дни отец кибернетики Норберт Винер был заведующим кафедрой электронной техники Калифорнийского университета. Он написал мне письмо и предложил работу в Калифорнийском университете в Беркли».
Лотфи Заде
(цитата: Visions of Azerbaijan)
Уже в 1963 году Заде стал заведующим кафедрой электротехники. Осознавая перспективы IT, он поменял её название, добавив специализацию computer science. Так Беркли стал первым в мире университетом со специалитетом по компьютерным наукам. Именно здесь учёный и создал свою необычную теорию.

Фото: Visions of Azerbaijan
Тени нечётких множеств
Заде чувствовал, что имеющиеся математические инструменты не способны описывать действительность, с которой люди сталкиваются в повседневной жизни.
«Идея, которая начала выкристаллизовываться в моём сознании в начале 1960-х годов, заключалась в том, что необходимо что-то сделать, чтобы преодолеть разрыв между миром математики и реальным миром. Эта идея легла в основу теории нечётких множеств».
Лотфи Заде
(цитата: IEEE Signal Processing Magazine)
Чтобы компьютеры могли решать интеллектуальные задачи, нужно было научить их понимать неоднозначные термины вроде «богатый», «молодой», «высокий», «тёплый» и так далее. Для этого требовалось в корне изменить математическое представление о множестве (то есть наборе элементов), существовавшее сотни лет. Разберём эту проблему подробнее.
В своей речи мы часто оперируем множествами, даже не подозревая об этом. Например, когда мы называем кого-то молодым, то формально делим всё человечество на «молодых» и «не молодых» людей. И таким образом причисляем обсуждаемого персонажа к множеству «молодых».
Заде понимал, что в реальном мире возраст, температура, богатство и большинство прочих оценочных категорий, которыми мы оперируем, имеют нечёткие границы. Практически всегда существуют переходные формы, при которых человек может быть «не совсем молодым», воздух в комнате «чуть тёплым» и так далее. Но как объяснить это бездушной машине?
Учёный предложил ввести понятие частичного вхождения элемента в множество, глубину которого можно измерять в пределах от 0 (полностью не принадлежит) до 1 (полностью принадлежит). Этот параметр Заде назвал «степенью принадлежности».
Теперь на языке математики можно было записать, что человек входит во множество «молодых» со степенью принадлежности 0,7 или температура соответствует множеству «тёплая» со степенью 0,2.
Очертания таких множеств Лотфи сравнил с тенями, которые предметы отбрасывают на стены. Он назвал эти множества «нечёткими», применив английское слово fuzzy, обозначающее нечто туманное и расплывчатое.
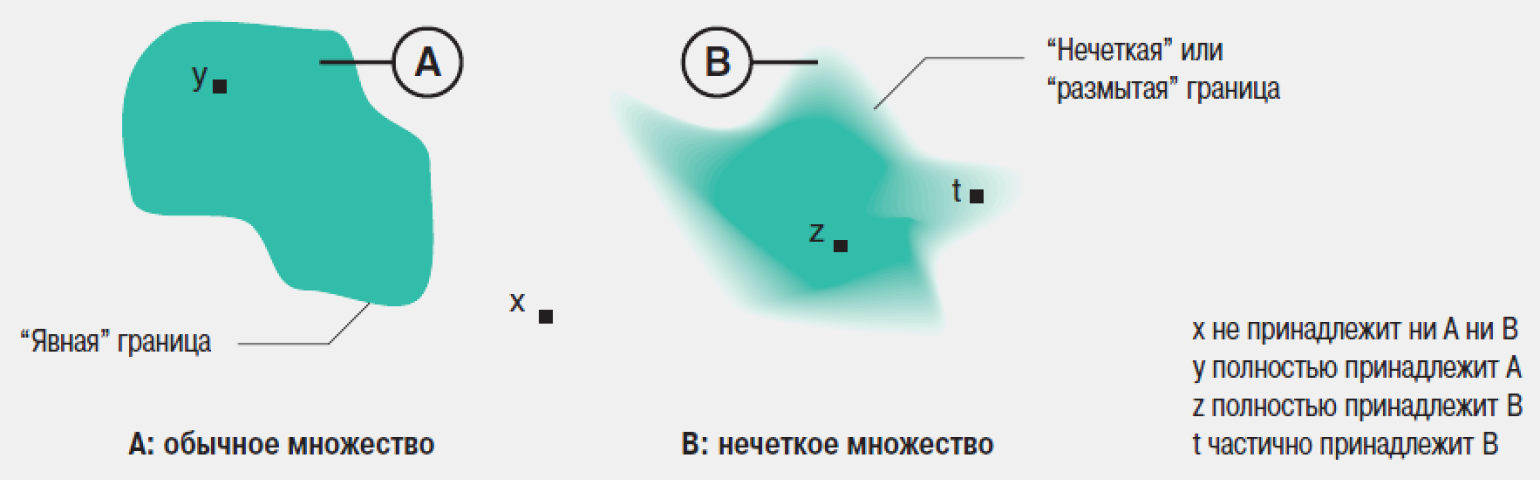
Изображение: «Нечёткая логика» / Техническая коллекция Schneider Electric / выпуск № 31, 2009
Столь радикальную идею научное общество могло принять в штыки — и Заде отдавал себе отчёт, что, выдвигая её, он рискует репутацией.
«Я отправил статью в журнал Information and Control, членом редакционной коллегии которого был сам. Считаю, что мою работу не опубликовали бы, не будь я сотрудником редколлегии».
Лотфи Заде
(цитата: IJCCC)
Чтобы подстраховаться, учёный также перевёл работу на русский и направил её в советский журнал «Проблемы передачи информации». Из-за бюрократических проволочек в СССР статья вышла лишь в 1966 году (на год позже, чем в США) под названием «Тени нечётких множеств».
От нечётких множеств к нечёткой логике
Много лет Лотфи Заде трудился над своей идеей, чтобы на её базе можно было программировать логику работы различных устройств и систем. Он признавался, что с 1965 года все его работы были связаны только с теорией нечётких множеств и нечёткой логикой.
В США к исследованиям Заде поначалу действительно отнеслись прохладно. Однако это не остановило учёного. Он популяризировал свои идеи в Европе и странах Азии. Много раз выступал на научных конференциях и в Советском Союзе, где свободно общался с коллегами на русском языке.
«Как я и ожидал, моя статья вначале вызвала неоднозначную реакцию, потому что нечёткость ранее никогда не рассматривалась в науке и технике».
Лотфи Заде
(цитата: IJCCC)
В 1973 году Заде ввёл в оборот понятие лингвистической переменной, которая может хранить слова и фразы естественного языка.
Например, лингвистическая переменная «температура» может иметь три базовых значения: «холодно», «тепло», «жарко». Каждое из этих значений описывается нечётким множеством, для которых нужно определить функцию (математическое выражение), задающую степень принадлежности.
Базовый набор значений можно расширить, введя переходные понятия вроде «очень тепло» или «не очень холодно».
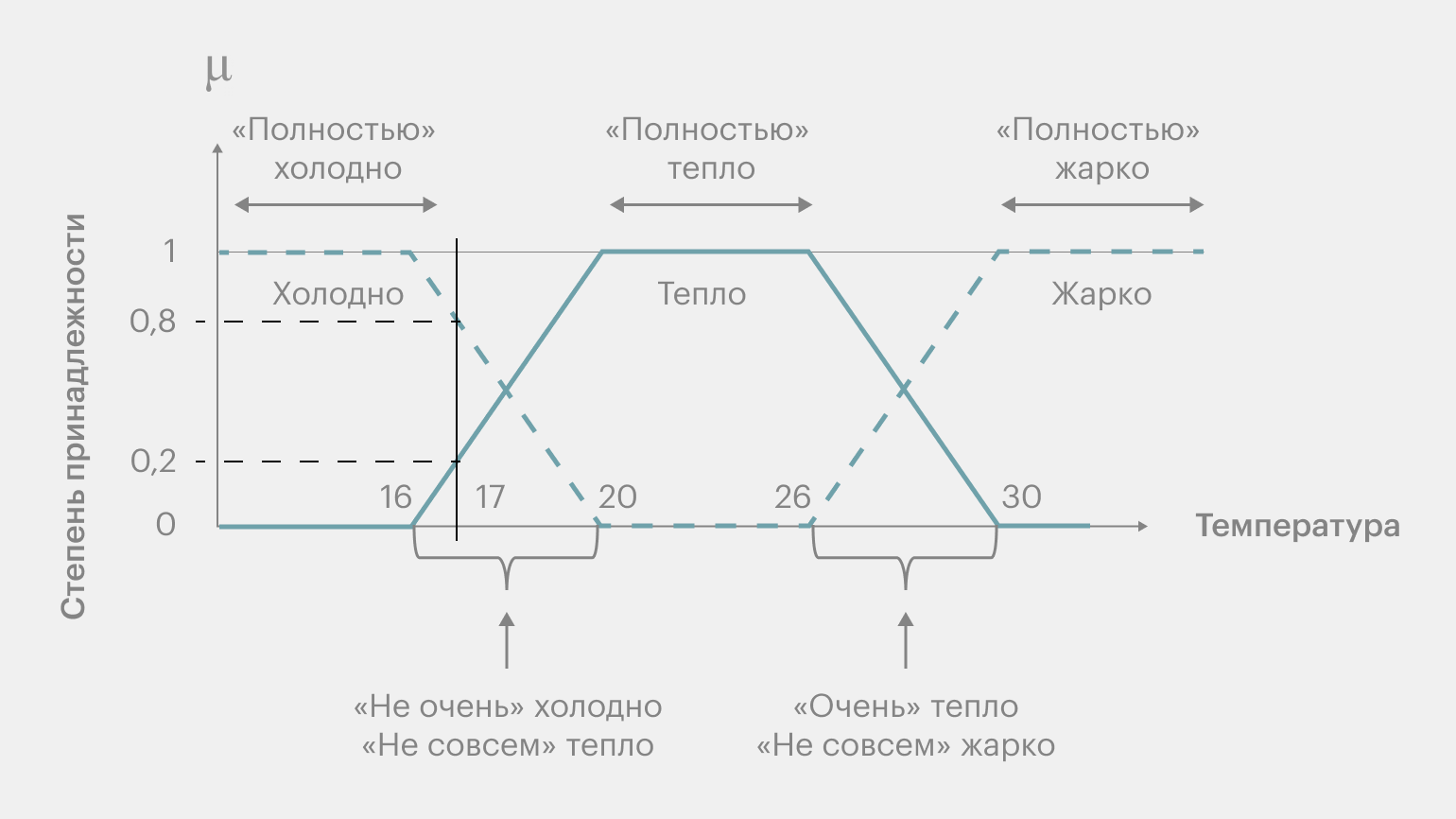
Изображение: Skillbox Media
Позднее Заде разработал приёмы, позволяющие работать с лингвистическими переменными подобно тому, как программисты работают с обычными логическими (Boolean) переменными.
Он определил правила для выполнения логических операций AND, OR, NOT над нечёткими высказываниями. В простейшем случае результатом операции «A AND B» будет минимум из степеней истинности A и B, а для операции «A OR B» — максимум.
Отрицание реализуется путём вычитания значения истинности из единицы. Например, если утверждение «холодно» истинно на 0,6, то результат выражения NOT «холодно» (можно записать как «НЕ холодно») будет иметь степень истинности 0,4.
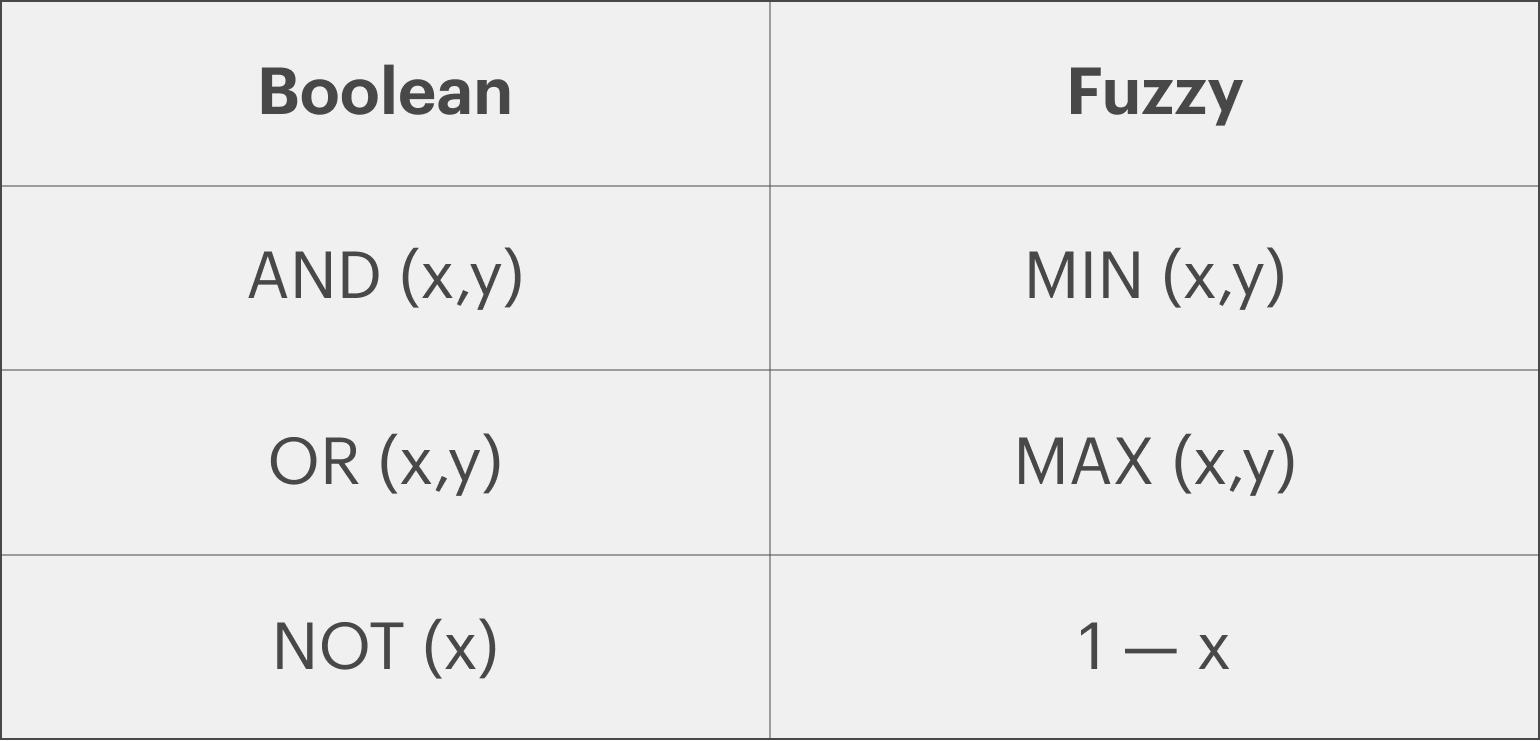
Изображение: Skillbox Media
Используя эти логические операции, разработчики вычислительных систем получили возможность составлять и программировать наборы (базы) нечётких правил, знакомые каждому программисту в виде IF — THEN. Например, для работы кондиционера можно составить правило вида: IF «тепло» AND «высокая влажность» THEN «средняя скорость вентилятора».
«Нечёткую логику можно рассматривать как формальное описание двух замечательных особенностей человека. Во-первых, возможности рассуждать и принимать рациональные решения на базе неопределённой, неполной и противоречивой информации. И, во-вторых, способности выполнять разнообразные задачи без точных измерений и вычислений».
Лотфи Заде
(цитата: Information Sciences)
Благодаря этим разработкам отношение к нечёткой логике значительно улучшилось. За 20 лет исследований Заде и его коллеги-учёные смогли превратить идею, казавшуюся вначале сомнительной, в стройную и непротиворечивую теорию, подкреплённую множеством теоретических выкладок.
«Нечёткая логика — точная логика, позволяющая работать с неточными и приблизительными рассуждениями. Парадоксально, но одним из главных достижений нечёткой логики является её способность формально определять то, что является неточным».
Лотфи Заде
(цитата: Information Sciences)
Поезда и двигатели с нечётким управлением
Заде предполагал, что предложенная им логика будет востребована в первую очередь в социальных и гуманитарных науках.
«Особенности нечёткой логики предполагают, что она может найти важные приложения в сферах экономики, лингвистики, юриспруденции и других областях, ориентированных на человека».
Лотфи Заде
(цитата: Information Sciences)
Однако его теория нашла широкое практическое применение и в технической сфере, чем учёный был приятно удивлён.
В 1975 году профессор Эбрахим Мамдани из Лондонского университета впервые продемонстрировал работающую нечёткую систему для управления паровой машиной. Это стало возможно благодаря придуманной им методике внедрения нечёткости в систему управления.
Проблема, которую решил британский учёный, состояла в том, что вычислительные устройства принципиально не рассчитаны на обработку нечёткой информации. Например, система управления кондиционером получает от датчиков конкретное число, характеризующее температуру (допустим, 17 °С). А затем выдаёт управляющие воздействия, оформленные в виде чётких числовых команд (например, включить вентилятор на 700 оборотов в минуту).
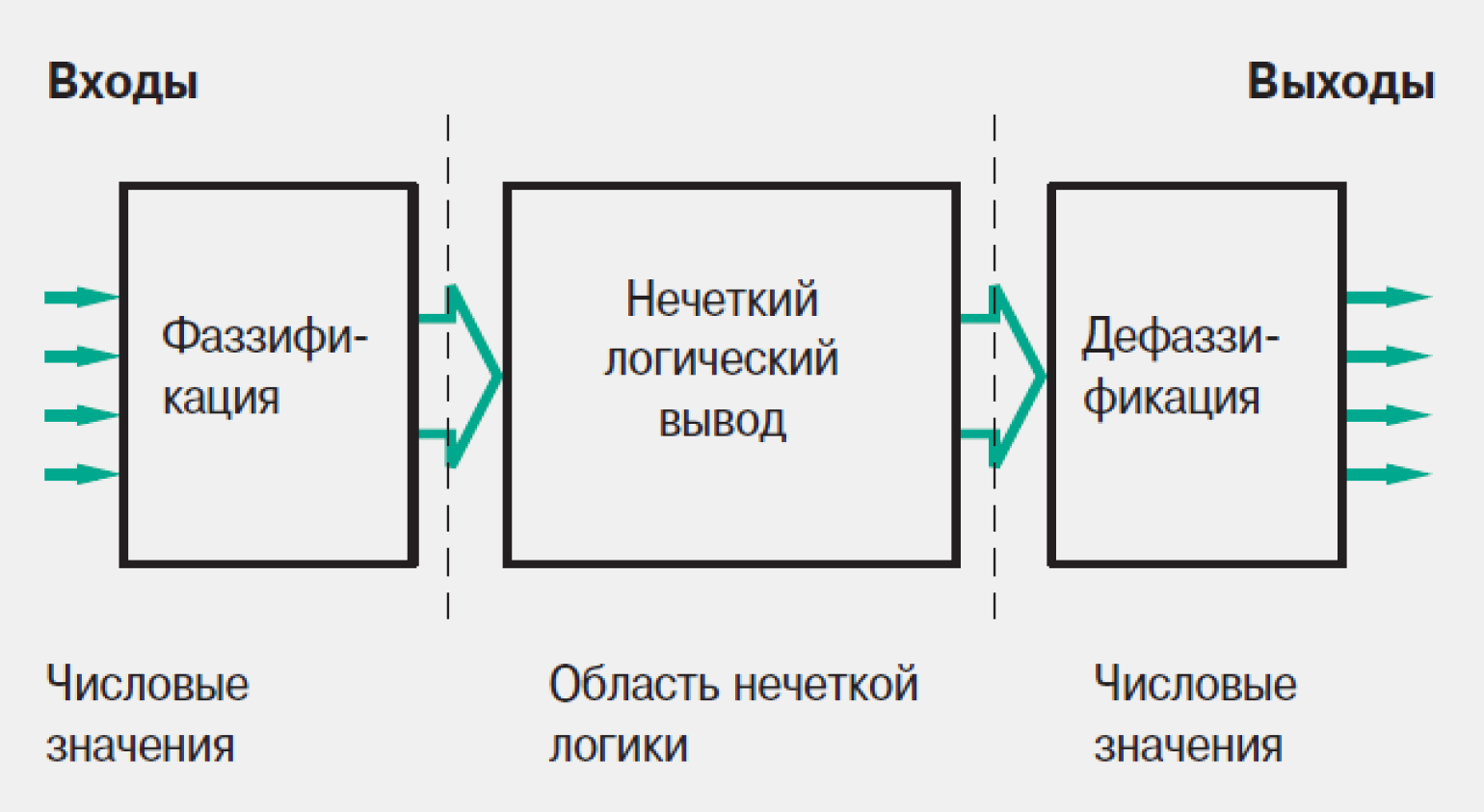
Изображение: «Нечёткая логика» / Техническая коллекция Schneider Electric / выпуск № 31, 2009
В соответствии с алгоритмом Мамдани в памяти компьютера хранятся наборы нечётких правил вида IF — THEN, сформированные на основе мнения экспертов, разбирающихся в специфике работы системы.
Далее нечёткая система работает следующим образом:
- Фаззификация. Преобразует все входные значения в нечёткие функции принадлежности.
- Нечёткий логический вывод. На базе хранимых в памяти правил вычисляет нечёткие выходные функции.
- Дефаззификация. Преобразует нечёткие результаты в чёткие выходные значения, которые используются для управления системой.
Японский профессор Мичио Сугено в середине 1980-х годов предложил свой, несколько отличающийся от метода Мамдани, вариант алгоритма, нацеленного на решение той же задачи. Модель Сугено впервые была применена в искусственном интеллекте, управляющем автомобилями, а затем — и скоростными поездами.
«В Японии теория нечётких множеств и нечёткая логика стали объектами обширных исследований и широкого применения, особенно в сфере потребительских товаров. Значимой вехой стала система метро в городе Сендай — система на основе нечёткой логики. Она была внедрена в 1987 году и считается очень успешной».
Лотфи Заде
(цитата: IJCCC)
Практически все нечёткие системы, созданные в дальнейшем, работают в соответствии с моделями Мамдани или Сугено.
Что может нечёткая логика и чего не может
С 1990-х годов нечёткую логику широко используют в различных системах управления — от сложных производственных процессов до бытовых приборов. На рынке появилось множество устройств, на корпусе которых красуется надпись «Fuzzy Logic», ставшая своеобразным символом ИИ.
Большое распространение получили стиральные машины, в системах управления которыми используется нечёткая логика. С её помощью ИИ проводит анализ таких факторов, как объём белья, тип порошка, уровень загрязнения, и выбирает оптимальный режим стирки из более чем 4000 возможных вариантов.
Возможно, ваш фотоаппарат оснащён нечёткой системой стабилизации изображения, а холодильник и кондиционер также работают по fuzzy-алгоритмам.

Фото: University of California, Berkeley
В автомобилях идеи Заде используются для мониторинга и обнаружения неисправностей, а также в автоматических «коробках» для более плавного и своевременного переключения передач.
В робототехнике нечёткая логика позволяет андроидам имитировать человеческое поведение, находить дорогу и избегать препятствий.
Как и предполагал Лотфи Заде, нечёткие принципы нашли своё применение и в гуманитарных науках: в социологии, в образовании — для оценки знаний, в экономике — для прогнозов по рынкам и инвестициям.
На базе нечёткой логики создаются экспертные системы, способные имитировать рассуждения специалистов в медицине, бизнесе, управлении персоналом, сфере безопасности и ликвидации чрезвычайных ситуаций.
Проработанная теория и наличие программных продуктов, позволяющих относительно легко оперировать нечёткостью, способствовали тому, что fuzzy-логика стала популярной темой научных исследований.
Однако у нечёткой логики есть и недостатки. Главный из них — правила должны строиться на основе экспертных знаний. Их получение, обработка и формализация являются сложной задачей. Эффективность работы нечёткой системы определяется квалификацией эксперта и качеством работы с полученной от него информацией.
В отличие от искусственных нейронных сетей, классические нечёткие системы не имеют возможности машинного обучения и не могут самостоятельно корректировать свою работу.
Чтобы преодолеть эту проблему, учёные пытаются «скрестить» технологии в так называемых нейронечётких системах, которые способны преодолеть ограничения нечётких систем и одновременно расширить пределы применения нейронных сетей.
Жизнь длиною в век
Лотфи Заде прожил 96 лет, работал до последнего дня. Даже на девятом десятке ежегодно выступал с докладами на 10–15 научных конференциях.
Многие из его поздних идей были столь новаторскими, что научный мир до сих пор пытается их осмыслить, а практическая реализация изобретений Заде ждёт своего часа в будущем.
Такими идеями были предложенные им:
- Нечёткие множества второго и последующих порядков, функция принадлежности к которым сама является нечёткой.
- Теория вычислений со словами и восприятиями, позволяющая математически извлекать из фраз их смысл и оперировать им.
- Гранулярные вычисления, работающие с «информационными гранулами», получаемыми в процессе извлечения знаний из информации.
В 1994 году Заде предложил термин «мягкие вычисления» (soft computing), в рамках которого объединил технологии создания ИИ-систем, основанные на неточных и приближённых методах решения сложных интеллектуальных задач.
К мягким вычислениям Лотфи Заде отнёс нейросети, нечёткую логику, эволюционные (генетические) алгоритмы, роевой интеллект (пчелиный, муравьиный и подобные им алгоритмы), искусственные иммунные системы. По мысли учёного, методы soft computing хорошо дополняют друг друга и должны использоваться совместно.
Лотфи был счастливо женат. Его супруга Фэй Заде, с которой он прожил 70 лет в браке, в 1998 году написала книгу My Life and Travels with the Father of Fuzzy Logic, считающуюся лучшей биографией учёного.
Заде скончался в 2017 году в своём доме в Беркли (США). Похоронили учёного, в соответствии с завещанием, на родине — на Аллее почётного захоронения в Баку.

Изображение: Google
Что читать и где программировать нечёткую логику
В 1976 году, когда в США нечёткая логика ещё считалась сомнительной теорией, в нашей стране была издана первая научная монография, состоящая из переводов на русский язык статей Лотфи Заде.
В последующие годы эта книга дополнялась новыми сведениями. Последнее её издание вышло в России в 2021 году. Начинать изучать сложную тему стоит именно с неё:
Заде, Л. Понятие лингвистической переменной и его применение к принятию приближённых решений / Л. Заде: пер. с англ. — М.: Лори, 2021. — 150 с. — ISBN 978-5-85582-423-0
Для более плотного погружения в тему и знакомства с математическими и научными основами сразу трёх основных технологий мягких вычислений также можно рекомендовать подробный учебник польских авторов, выдержавший два переиздания в России:
Рутковская, Д. Нейронные сети, генетические алгоритмы и нечёткие системы: пер. с польск. И. Д. Рудинского: учебное пособие / Д. Рутковская, М. Пилиньский, Л. Рутковский. — 2-е изд. — М.: Горячая линия-Телеком, 2013. — 384 с. — ISBN 978-5-9912-0320-3
А в качестве нормативной документации стоит ознакомиться с ГОСТ Р МЭК 61131-7-2017 «Контроллеры программируемые. Часть 7. Программирование нечёткого управления». Помимо прочего, в этом стандарте описан язык нечёткого управления (FCL, Fuzzy Control Language).
«Hello, World!» с помощью FCL не напишешь (да, это и не требуется), а вот описать нечёткую систему управления вполне получится. И помочь в этом могут библиотеки вроде jFuzzyLogic, которая подключается в виде плагина к IDE Eclipse.
Хотя, конечно, более популярным способом работы с нечёткой логикой является использование пакета Fuzzy Logic Toolbox в среде математического моделирования Matlab либо инструментов вроде программы fuzzyTech, позволяющих создавать системы, основанные на нечёткой логике, и вовсе без программирования, оперируя только при помощи мыши.










