Ползай, как муравей, летай, как пчела: алгоритмы, которые придумала сама природа ??
Рассказываем, как муравьи с пчёлами помогли программистам и математикам создать новые алгоритмы.


Многие интересные технические решения люди подсмотрели у животных и растений. Например, крылья птиц вдохновили первых авиастроителей на создание самолётов, а колючки репейника способствовали появлению застёжек-липучек.
Учёные-информатики тоже подглядывают за окружающим миром в поисках лучших решений. Они называют алгоритмы и модели, позаимствованные у природы, биоинспирированными — то есть навеянными живой природой.
Пожалуй, самая популярная биоинспирированная модель — искусственные нейронные сети, которые имитируют работу клеток человеческого мозга. Однако в этой статье мы расскажем о менее известных моделях: муравьином алгоритме и алгоритме пчелиной колонии. Учёные разработали их, наблюдая за работой тысяч насекомых, которые совместно решали невообразимо сложные задачи.
Роевой интеллект
Мы привыкли думать о муравьях как о мудрых существах: они строят огромные гнёзда, занимаются «скотоводством» и даже захватывают сородичей в рабство. Но парадокс в том, что отдельно взятый муравей очень глуп. Только действуя сообща, эти насекомые способны добиваться впечатляющих результатов. Особи с примитивными рефлексами взаимодействуют между собой и демонстрируют удивительно эффективное поведение.
Долгие годы учёные пытались понять механизмы функционирования муравьиного общества. Особенно их занимал один факт: передвигаясь от муравейника к источнику пищи, насекомые всегда выбирали самый короткий путь. Сначала явление пытались объяснить таинственными психополями, с помощью которых муравьи якобы взаимодействуют между собой.
К счастью, бельгийский исследователь Марко Дориго создал математическую модель, научно описывающую этот процесс. Он опубликовал её в докторской диссертации в 1992 году и реализовал в виде компьютерного алгоритма. Модель муравьиного алгоритма (Ant Colony Optimization, ACO) Дориго привлекла других учёных к изучению роевого интеллекта (Swarm intelligence).
Роевой интеллект описывает системы, состоящие из множества особей — их называют агентами. Агенты могут быть как реальными роботами, так и виртуальными объектами в компьютерной симуляции. Они взаимодействуют между собой по определённым правилам и вместе находят решение общей задачи.
За 30 лет с момента открытия муравьиного алгоритма учёные создали несколько десятков биоинспирированных моделей. А на основе роевого интеллекта реализовали модели, имитирующие колонии пчёл, светлячков (Firefly Algorithm) и косяка рыб (Fish School Search).
Тропа из феромонов
Выбор кратчайшего маршрута при движении муравьёв к пище учёные объяснили способностью использовать феромоны — пахучие выделения, которыми насекомые отмечают свой путь. Особенность феромонов в том, что они быстро испаряются и теряют свою пахучесть.
В общем виде процесс выглядит так. Вначале муравей-разведчик исследует прилегающую территорию и постепенно отдаляется от муравейника. Когда он обнаруживает что-то вкусное (например, упавшее на землю яблоко), то возвращается в гнездо и помечает феромонами путь до места с едой.
Оставленный им запах привлекает других муравьёв. Но путь, который выбрал разведчик, скорее всего, не самый короткий. Они пойдут по нему к пище, но некоторые будут случайно отклоняться от первоначальной траектории.
Все альтернативные пути, обнаруженные муравьями, тоже помечаются феромонами. Таким образом, каждый муравей, идущий от гнезда к яблоку, будет постоянно попадать на развилки из дорожек феромонов. Муравей выбирает путь по простому правилу: идти по дорожке с наиболее сильным запахом.
Феромоны быстро улетучиваются. Очевидно, что по короткому маршруту за единицу времени пройдёт больше муравьёв, чем по длинному. С каждым новым проходом муравья короткая дорожка будет становиться более пахучей и привлекательной, а неэффективные длинные маршруты — исчезнут из-за испарения феромонов.
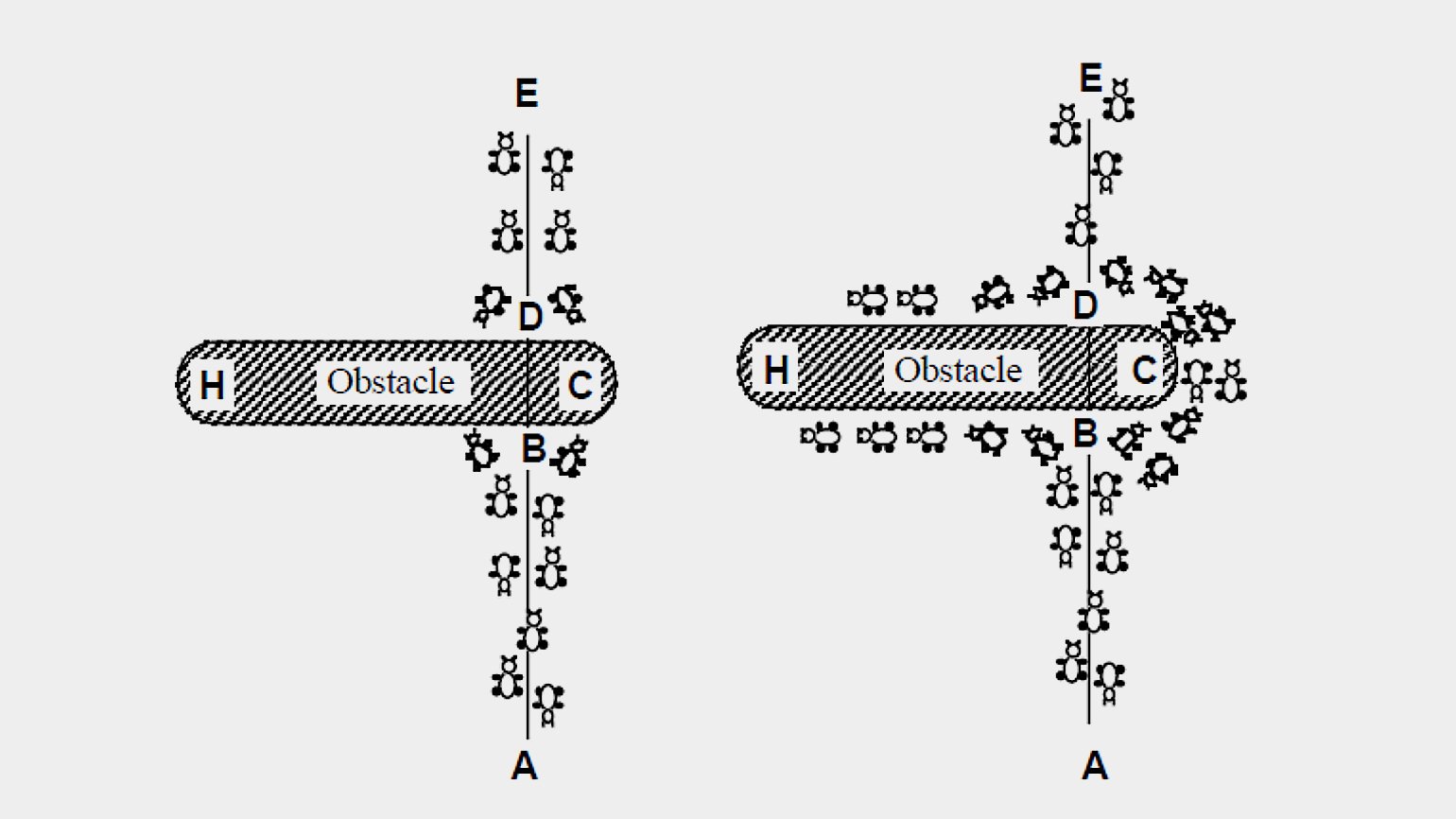
Изображение: M. Dorigo, V. Maniezzo, A. Colorni / «Ant System: Optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybernetics — Part B» / PubMed, 1996
Через некоторое время практически все насекомые будут идти по самой короткой дорожке. Отдельные сбившиеся с пути особи уже ничего не изменят: перемещаясь по феромонной тропе, рой будет поддерживать её сильный запах.
Как реализовать муравьиный алгоритм
Проблема, которую решают муравьи, похожа на задачу странствующего торговца (коммивояжёра): нужно по одному разу посетить несколько городов, пройдя между ними по самому короткому маршруту, и вернуться в исходную точку.
Особенность задачи в том, что даже при небольшом количестве городов компьютеру потребуется несколько миллиардов лет на перебор всех вариантов. А вот с муравьиным алгоритмом решить задачу можно гораздо быстрее.
Для удобства дорожную сеть, по которой движется коммивояжёр (в нашем случае — муравей), обычно изображают в виде графа, где точки соответствуют городам, а рёбра — дорогам между городами. При компьютерной реализации муравьиного алгоритма в программу вводят количество точек и длины всех путей.
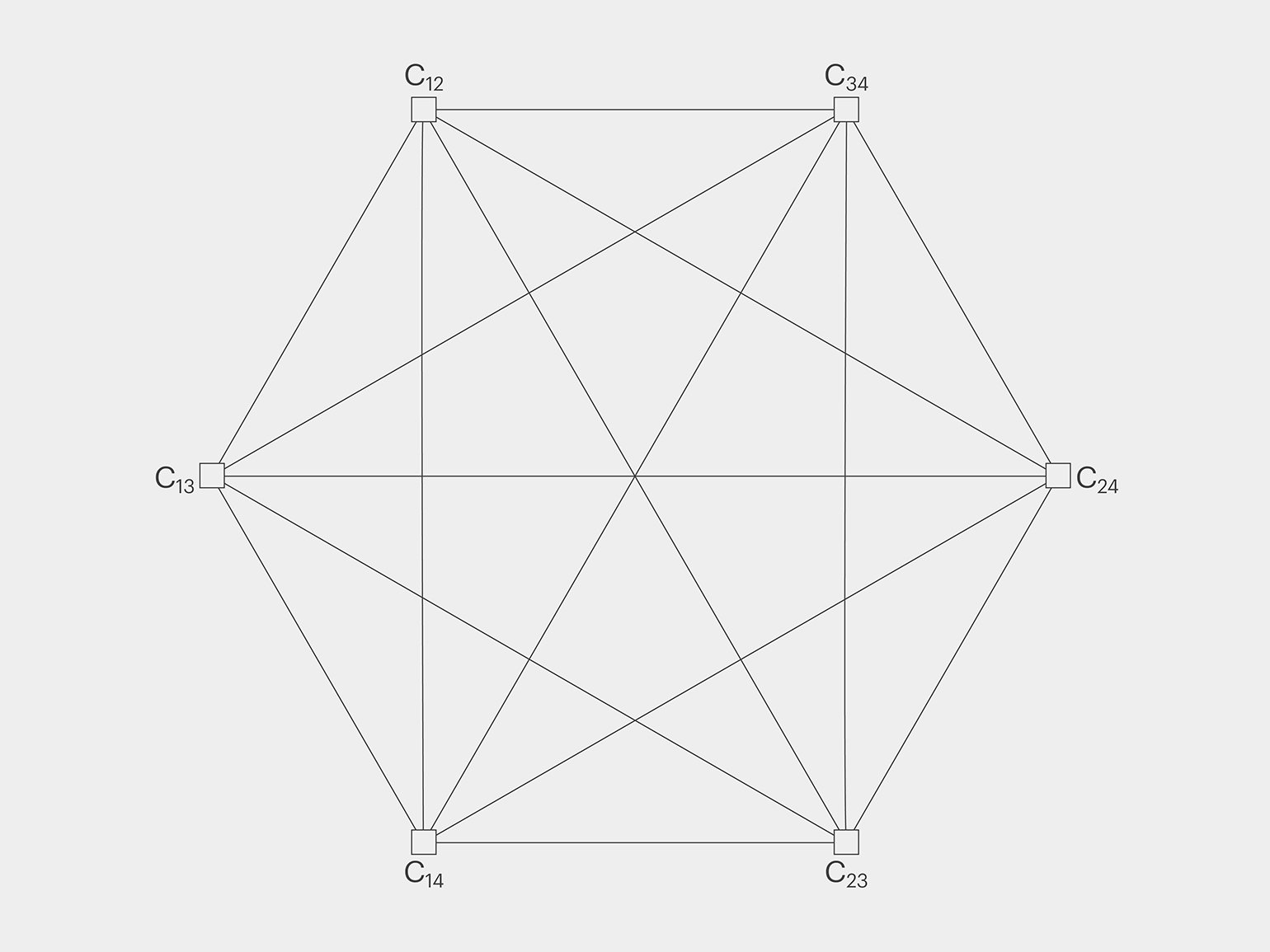
Инфографика: Майя Мальгина / Skillbox Media. Источник: Александр Цуриков
До начала работы алгоритма определим константы: коэффициент испарения феромона и коэффициент его влияния на выбор нового маршрута.
Затем создадим переменные для хранения вещественных чисел, которые соответствуют количеству феромона на каждом ребре графа. Возможному пути между точками будут соответствовать два числа — его длина и количество феромонов. Длина — величина постоянная, а вот количество феромонов будет изменяться с каждой итерацией цикла.
Одна итерация цикла равна одному проходу муравья по замкнутому маршруту. Чем больше итераций, тем больше условных муравьёв пройдёт по дорожной сети и тем выше вероятность нахождения кратчайшего маршрута. Когда сработает условие выхода (это может быть, например, заранее заданное число итераций), цикл завершится, а программа сохранит оптимальный маршрут.
Псевдокод алгоритма:
Загрузка графа (дорожной сети)
Инициализация переменных и определение констант
ЦИКЛ (до достижения условия выхода)
Инициализация муравьёв
Поиск решений
Обновление феромона
КОНЕЦ ЦИКЛА
Сохранение результата
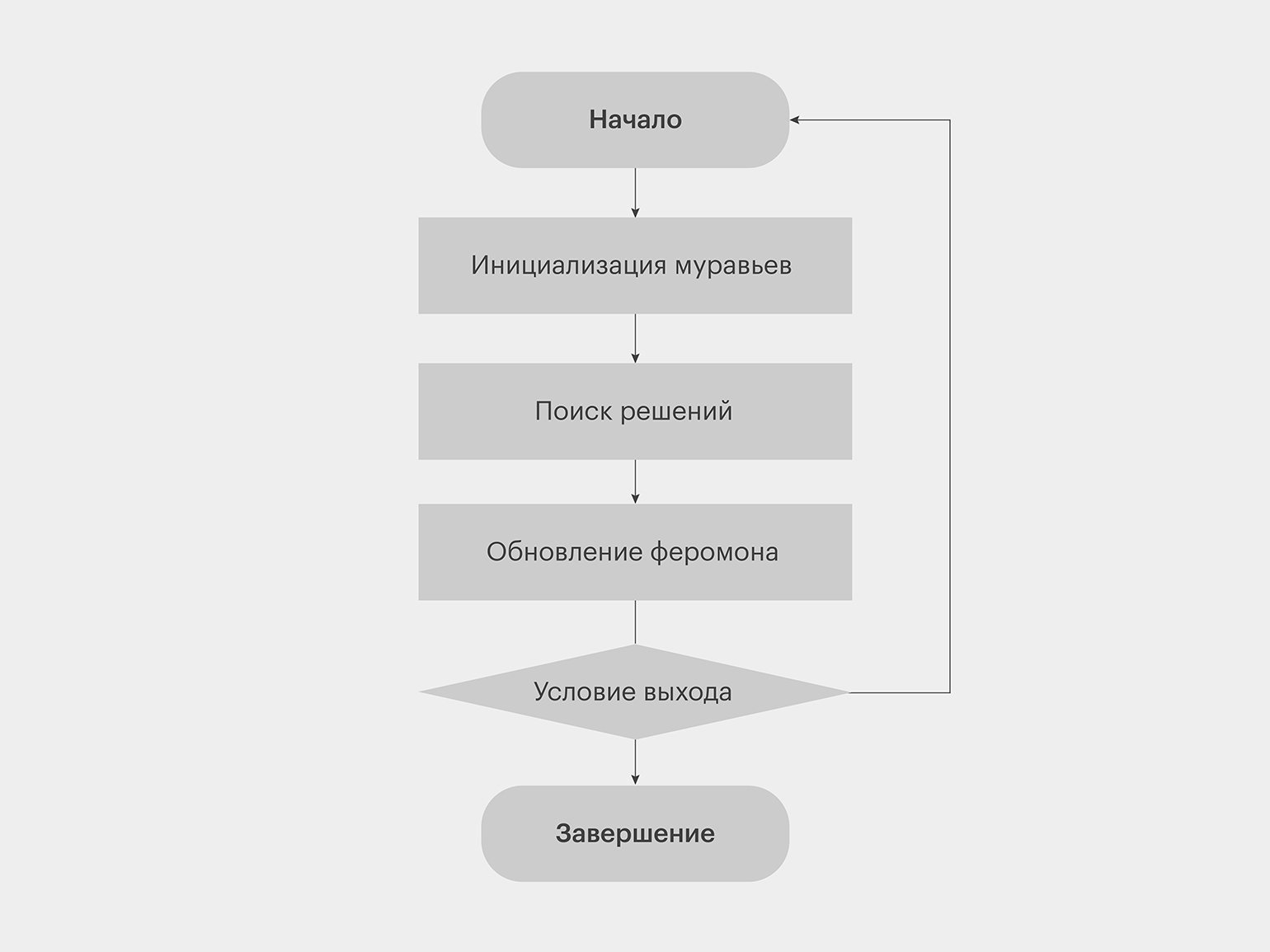
Заметьте: в каждой итерации муравьи инициализируются заново. Так мы моделируем поиск пути из новой точки (это возможно, поскольку мы ищем замкнутый маршрут).
В каждом узле графа муравей, следуя простому правилу, принимает решение, по какому из возможных маршрутов ему продолжить своё движение. Муравей выбирает следующую точку для посещения с вероятностью, прямо пропорциональной количеству феромона на пути и обратно пропорциональной длине пути.
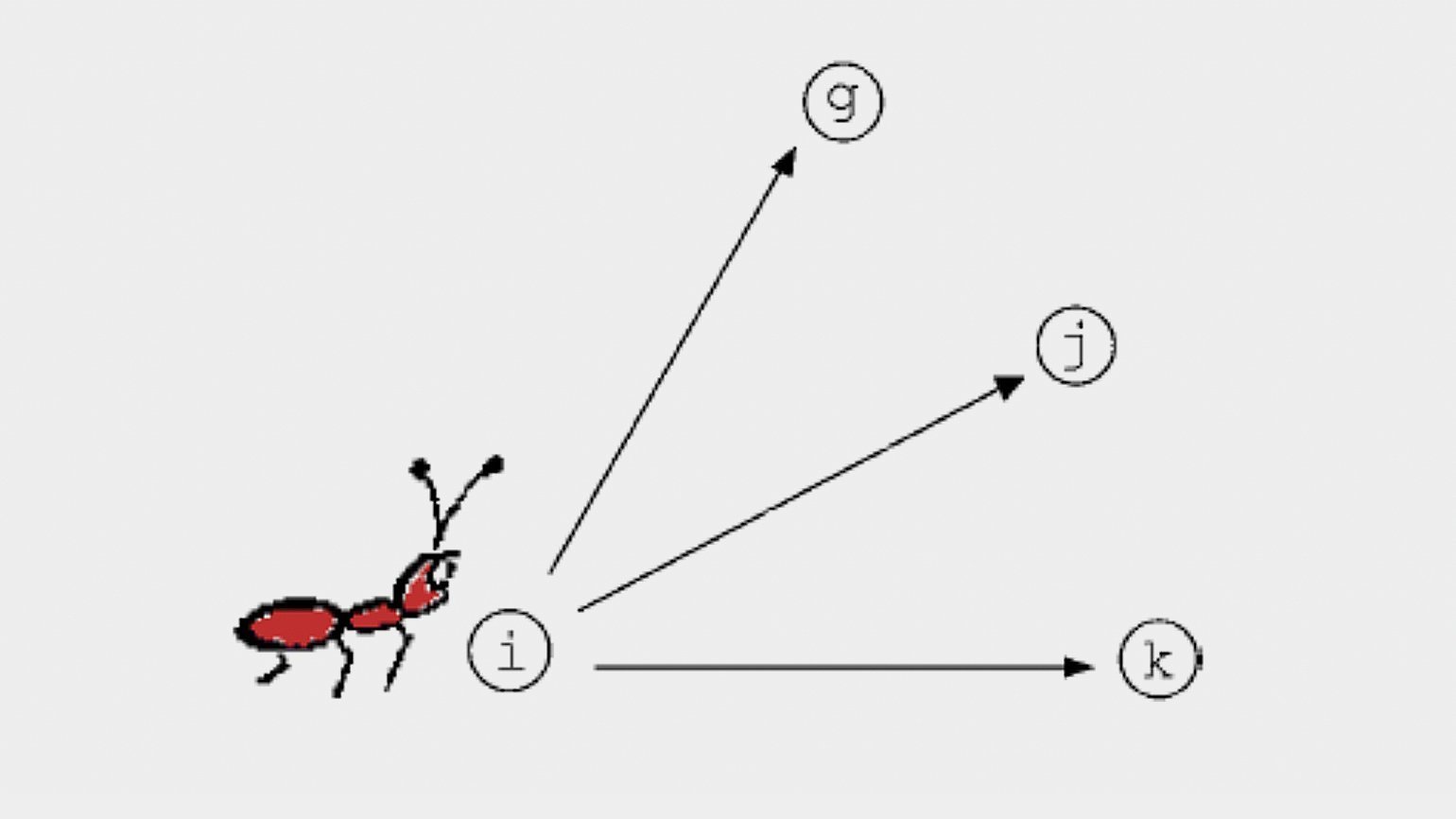
Изображение: M. Dorigo, M. Birattari, T. Stützle / Ant Colony Optimization / IEEE Computational Intelligence Magazine, 2006
После того как муравей прошёл весь маршрут и оказался в исходной точке значения переменных с количеством феромонов на каждом ребре графа обновляются.
Сначала они умножаются на дробный коэффициент испарения (константа) и таким образом уменьшаются. А на путях, по которым прошёл муравей, количество феромона увеличивается обратно пропорционально длине пути: чем короче путь, тем больше феромона прибавляем.
Процесс многократно повторяется: муравьи начинают движение из новых узлов графа. Уровни феромонов, привязанные к каждому ребру, несут информацию о предыдущих проходах виртуальных насекомых. После выхода из цикла маршрут, на котором осталось наибольшее количество феромонов, сохраняется как оптимальный.
Есть несколько вариаций муравьиного алгоритма. Например, в модели могут быть элитные особи, которые перемещаются по лучшим маршрутам и оставляют больше феромонов, чем их обычные братья.
Учёные доказали сходимость некоторых версий алгоритма. Иными словами, чем дольше муравьи будут ходить между точками графа, тем лучшие решения будет выдавать алгоритм.
Танцы и пчёлы
Пчёлы тоже демонстрируют удивительные способности к поиску оптимальных решений. Полосатые труженицы находят скопления цветов для сбора нектара и пыльцы в нескольких километрах от улья, а затем «рассказывают» о них товарищам с помощью… танца.
Да, пчёлы способны передавать друг другу информацию с «географическими координатами» посредством ритмических движений. При этом по интенсивности танца сородичей пчёлы делают выводы о количестве цветов в указанной точке пространства (чем больше цветов — тем активнее движения). Это необычное явление обнаружил в середине XX века исследователь насекомых Карл Фриш. За свои работы он был удостоен Нобелевской премии.
В течение многих лет только учёные-биологи исследовали пчелиные методы поиска. А в 2005 году их результатами заинтересовался профессор Дервис Карабога, работавший на кафедре вычислительной техники в турецком университете Эрджиес (Erciyes University). Он опубликовал научную статью и описал в ней модель роевого интеллекта, на создание которой его вдохновили пчелиные танцы. Модель получила название «алгоритм пчелиной колонии» (Artificial Bee Colony).
Как реализовать алгоритм пчелиной колонии
Все пчёлы разделяются на 3 вида: разведчики, рабочие и наблюдатели. Вначале несколько разведчиков вылетают из улья в разных случайно выбранных направлениях. Обнаружив нектар, они возвращаются в улей и рассказывают на «танцполе» пчёлам-наблюдателям о местах своих находок.
По интенсивности танца наблюдатели выбирают разведчиков, которые обнаружили наиболее богатые нектаром площадки, и вылетают в нужном направлении. На месте сбора нектара наблюдатели превращаются в рабочих пчёл. Они облетают это место и оценивают число цветов. Дальше возможны два варианта.
Первый: пчела находит поблизости другую площадку с большим количеством цветов и собирает нектар оттуда, а про старое место забывает. Затем она возвращается в улей, где в танце сообщает пчёлам-наблюдателям координаты нового источника нектара.
Второй: пчела не находит лучшего места и собирает нектар там, куда изначально летела. Дома она рассказывает пчёлам о той же точке.
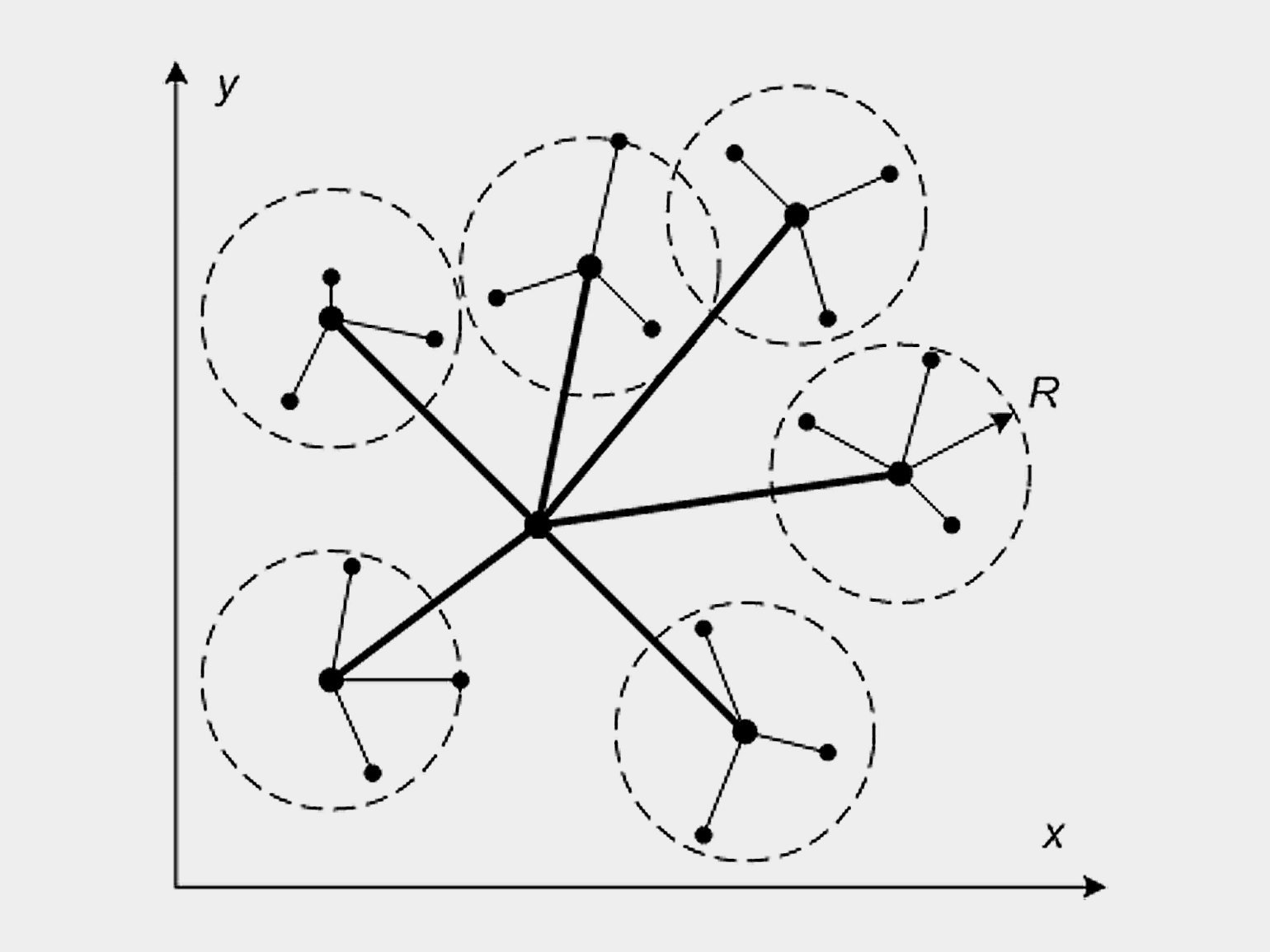
Изображение: Wikimedia Commons
Процесс повторяется многократно. Прилетев в улей, пчёлы-рабочие сообщают в танце параметры места, с которого собрали нектар, и превращаются в наблюдателей. В следующей итерации они выбирают по танцам своих сородичей новую привлекательную точку, вылетают туда и снова становятся рабочими.
Через некоторое время все пчёлы сосредоточатся на сборе пыльцы и нектара из лучших источников, а координаты менее богатых цветами точек просто забудут.
Псевдокод алгоритма:
Инициируются несколько случайно выбранных разведчиками точек — их параметры доступны на «танцполе»
ЦИКЛ (до достижения условия выхода)
Выбрать на «танцполе» точку с наиболее привлекательными параметрами, сохранить её координаты и вылететь к ней
Кружить некоторое время неподалёку от выбранной точки, постоянно сравнивая количество цветов
ЕСЛИ (количество цветов под пчелой > количества цветов в точке, выбранной на «танцполе»), ТО (сохранить координаты новой точки)
Собрать нектар
Вернуться в улей
Сообщить на «танцполе» параметры точки, с которой собрали нектар
Удалить с «танцпола» точку (или точки) с наихудшими параметрами
КОНЕЦ ЦИКЛА
Сохранение результата
Хранить лучшие решения можно в массиве фиксированной длины — он будет выполнять роль «танцпола». Цикл выполняется, пока не выполнятся условия его завершения.
Есть целое сообщество специалистов, которые обеспечивают развитие алгоритма пчелиной колонии. Их версию псевдокода можно найти по ссылке. На официальной страничке сообщества также можно скачать реализации модели на Java, C#, Python и других языках программирования.
Где это можно использовать
Модели роевого интеллекта уже применяют там, где из множества решений нужно выбрать самое оптимальное.
- Поисково-спасательные операции. Учёные из Курчатовского института запрограммировали группу роботов с помощью роевого интеллекта. Роботы находят предметы, разбросанные по локации, и перетаскивают их в точку сбора по кратчайшему маршруту. При этом муравьиный алгоритм хорошо подходит для устройств, движущихся по поверхности земли, а пчелиный — для летающих (дронов, квадрокоптеров).
- Автомобильные грузоперевозки. Европейская компания Ant Optima разрабатывает системы, оптимизирующие перевозку грузов на автомобилях. Её программисты написали на основе муравьиного алгоритма ряд компьютерных программ для доставки продуктов питания, медикаментов и нефтепродуктов по городам и торговым точкам. Софт Ant Optima отслеживает количество товара на складах, мониторит обстановку на европейских дорогах и помогает выбрать оптимальный маршрут для доставки грузов.
- Гражданская авиация. Роевой интеллект помогает авиакомпании Southwest Airlines выбирать места для стоянки самолётов и оптимизировать поток пассажиров, которые покупают билеты и проходят регистрацию. Так авиаперевозчик борется с очередями возле касс и стоек регистрации.
- Градостроение и наука. С помощью муравьиного алгоритма учёные определяют оптимальное расположение электростанций, трансформаторов и линий электропередач, а также разрабатывают дизайн формы портативных антенн.
А вот британские учёные предложили создавать объёмные рисунки с помощью муравьиного и птичьего алгоритмов. Они даже придумали термин «роевое искусство» (Swarm Art).
Исследователи нарисовали простейшие контуры объектов, а затем пустили по ним виртуальную стаю. Перемещаясь вдоль нарисованных линий, виртуальные животные за несколько итераций алгоритма придали рисункам объём.
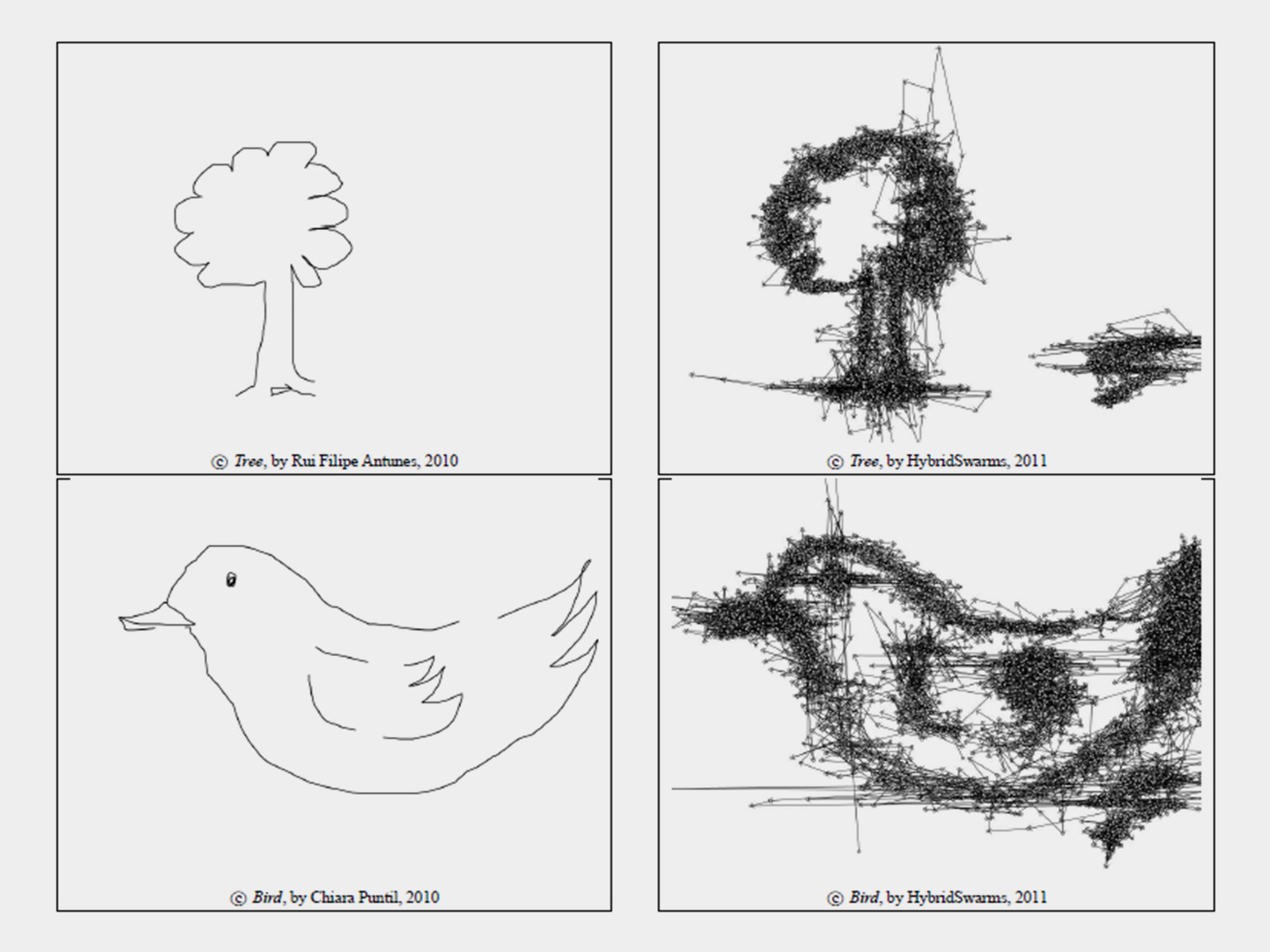
Изображение: M. M. Al-Rifaie, J. M. Bishop, A. Aber / Creative or Not? Birds and Ants Draw with Muscles / AISB 2011: Computing and Philosophy, 2011
Крупным IT-компаниям всё чаще нужны знатоки искусственного интеллекта. Поступайте на онлайн-бакалавриат по Data Science & Machine Learning и становитесь востребованным IT-специалистом с дипломом государственного вуза.