Линейная функция: график, формула и свойства
Прямая линия — тоже график.


Графики многих математических функций сложные, извилистые и зависят от нескольких факторов — например, смещения, периодичности и преобразований. Другое дело — линейная функция. Её график выглядит как обычная прямая на координатной плоскости. В этой статье рассказываем, что такое линейная функция, какими свойствами она обладает и как построить её график.
Содержание
Что такое линейная функция
Представьте, что вы каждый месяц откладываете фиксированную сумму на отпуск. В таком случае итоговая сумма накоплений будет зависеть от количества месяцев, а рассчитать её можно будет с помощью формулы S = k × m. В ней S — итоговая сумма, k — ежемесячное пополнение копилки, m — количество месяцев.
Если у вас остались деньги с прошлого отпуска, то наверняка вы начали копить не с нуля. В таком случае в формуле появится b — начальная сумма: S = k × m + b.
Рассмотрим, как эта формула будет выглядеть в системе координат XY, в которой вертикальная ось X — месяцы, а горизонтальная ось Y — накопленная сумма.
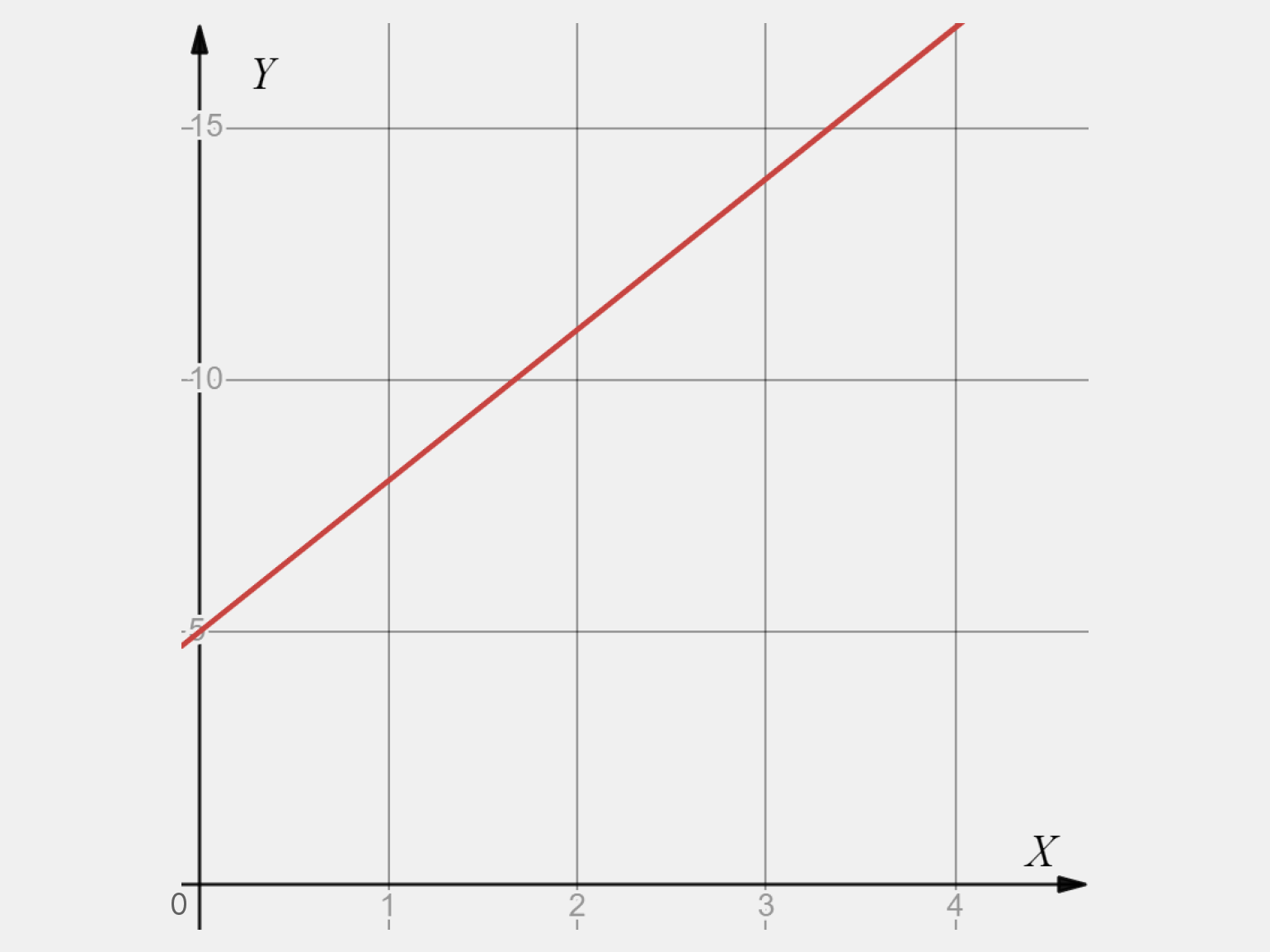
Инфографика: Skillbox Media
Полученный график и есть линейная функция. В нашем случае она равномерно увеличивается, так как мы пополняем копилку каждый месяц.
Определение линейной функции
Если давать формальное определение, линейная функция — это простая математическая функция, которая описывает прямую линию на графике. В общем виде её уравнение можно записать следующим образом:
y = kx + b
В этом уравнении:
- у — значение функции;
- х — независимая переменная;
- k — коэффициент наклона;
- b — свободный член, который показывает, где линия пересекается с осью Y.
Свойства линейной функции
У линейной функции есть несколько важных свойств, которые её описывают. Давайте разберём их.
Угловой коэффициент
Угловой коэффициент k определяет наклон графика линейной функции и описывает, как быстро меняется значение y по сравнению с x. Он влияет на направление и угол наклона линии, а ещё с его помощью можно понять, как изменяется функция:
- Если k > 0, график наклонён вправо и функция будет возрастающей.
- Если k < 0, график наклонён влево и функция будет убывающей.
- Если k = 0, функция постоянна, и график у = b представляет собой горизонтальную линию, параллельную оси X.
Чем больше по модулю значение k, тем больше угол между графиком и осью X. Например, если k = 1, то наклон прямой будет 45 градусов. Если увеличить угловой коэффициент до 2, прямая будет расти быстрее, а угол наклона увеличится.
Угловой коэффициент k также показывает, на сколько единиц изменится y, если x изменится на одну единицу. Например, если k = 2, то при увеличении x на одну единицу y увеличивается на две единицы. Этот принцип отражает постоянный темп изменения y по отношению к x.
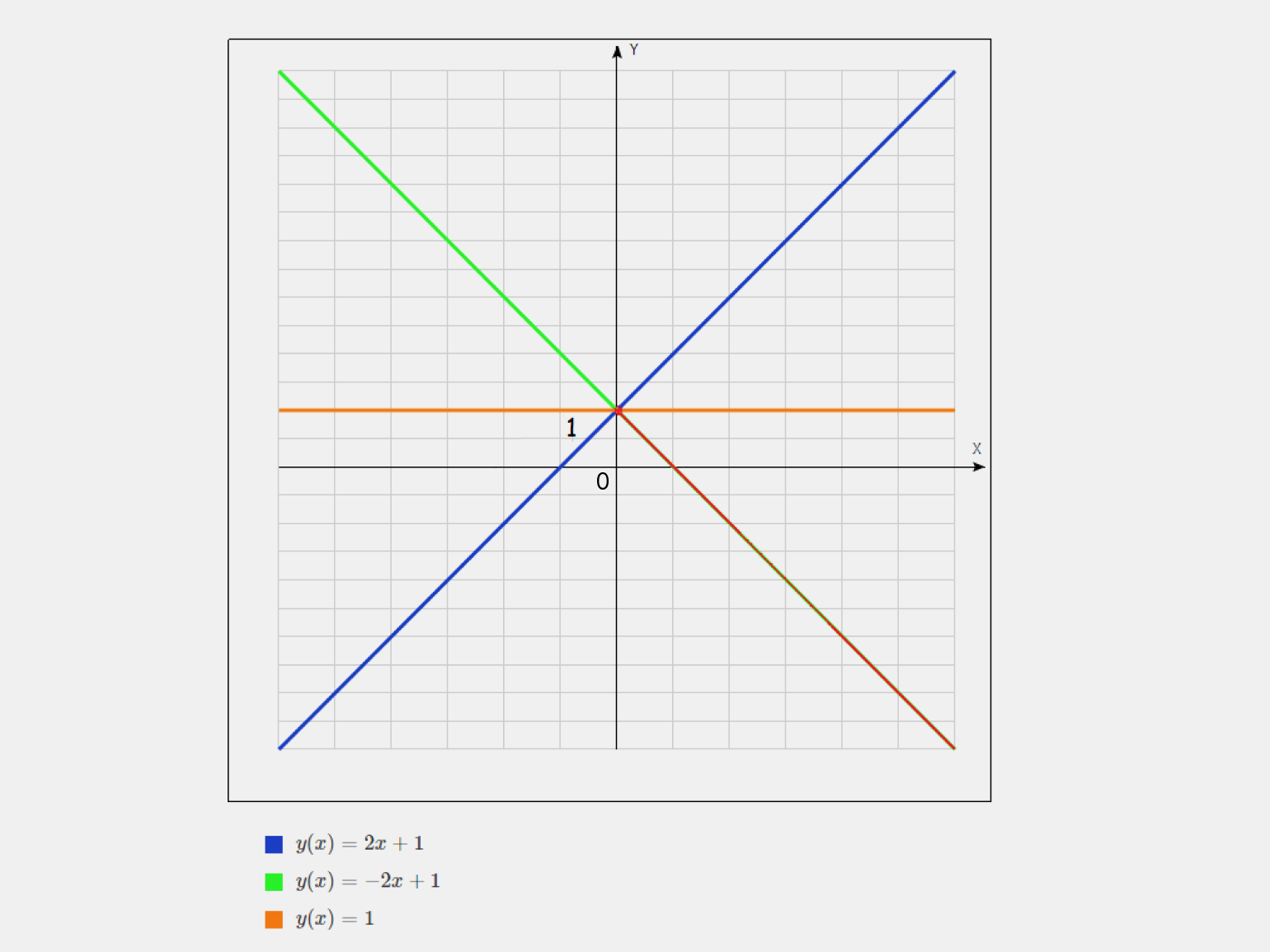
Инфографика: Skillbox Media
Свободный член b
Свободный член b показывает, в какой точке график пересекается с осью Y и сдвигает его вверх или вниз. Он не влияет на наклон линии, а только на её положение по высоте:
- Если b > 0, прямая пересекает ось Y выше начала координат.
- Если b < 0, прямая пересекает ось Y ниже начала координат.
- Если b = 0, то линейная функция принимает вид y = kx. Такая функция называется прямо пропорционально, и её график проходит через начало координат.
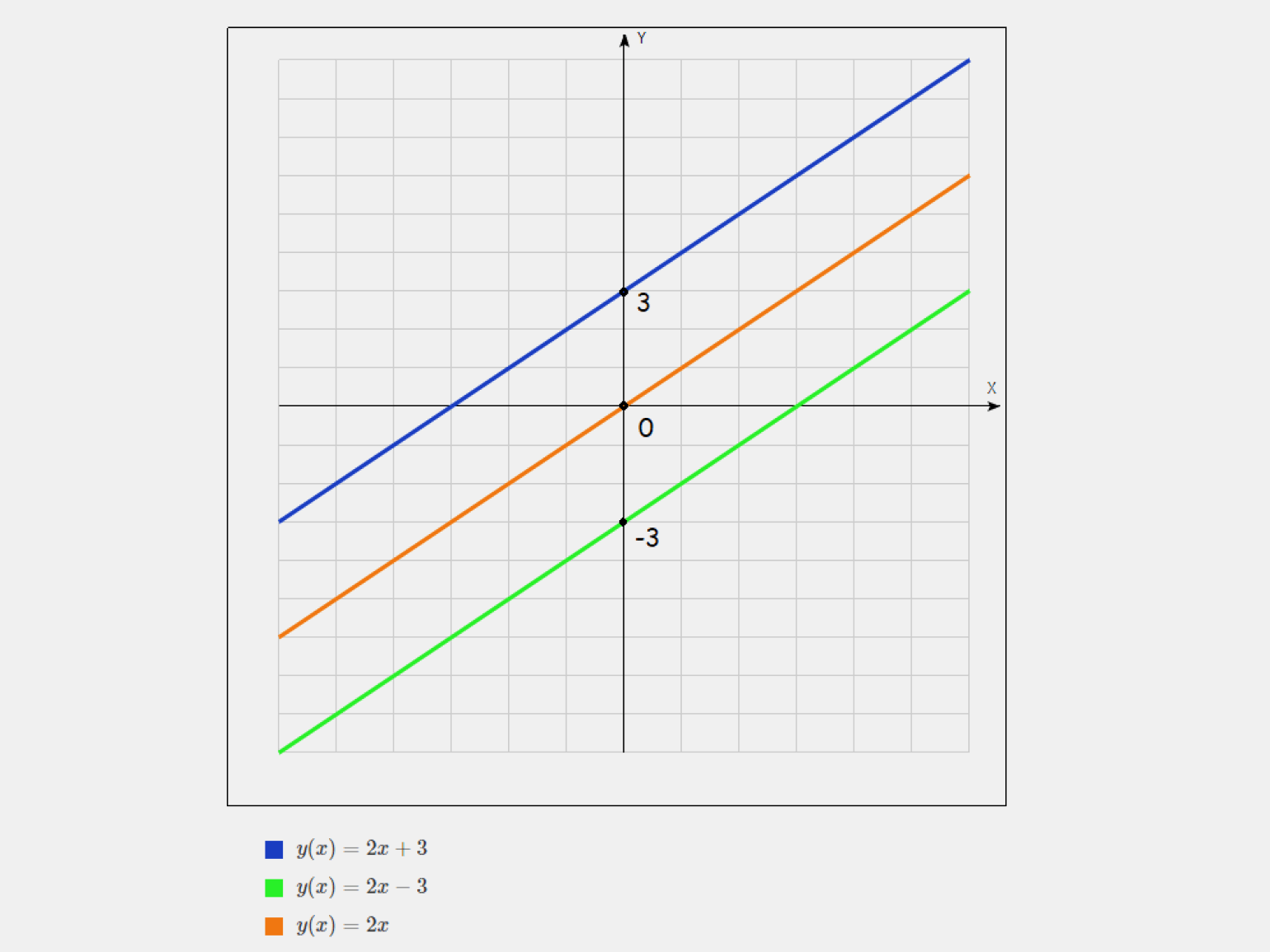
Область определения функции
Область определения функции — это все значения, которые может принимать переменная x. Для графика функции y = kx + b область определения включает все действительные числа. В общем виде это можно записать так:

Читайте также:
Область значений функции
Область значений функции — это значения, которые может принимать переменная y при различных x. Область значения графика линейной функции также включает в себя все действительные числа. В общем виде это записывается следующим образом:
Если k = 0, то область значений функции будет включать только одно значение y = b.
Непрерывность
Линейная функция y = kx + b — непрерывная, так как её график представляет собой прямую линию без разрывов и скачков. Для любого значения x функция ведёт себя предсказуемо, и изменение x приводит к пропорциональному изменению y. Непрерывность линейной функции означает, что её график можно нарисовать одним движением, например, с помощью линейки.
Точки пересечения с осью X
График линейной функции y = kx + b пересекает ось X в точке x = −b / k при k ≠ 0. При k = 0 точек пересечения нет, так как уравнение превращается в у = b — это прямая линия, которая параллельна оси X и не пересекает её.
Обратимость
Обратимость — это возможность найти обратную функцию, которая позволяет выразить переменную x через переменную y. Основное условие обратимости линейной функции — это k ≠ 0.
Чтобы найти обратную линейную функцию, надо сперва выразить x через y:
После этого можно записать обратную функцию в следующем виде:
Чётность
Чётность функции показывает, как она ведёт себя при замене x на −x:
- Чётная функция: при замене x на −x значение не меняется, то есть f(−x) = f(x).
- Нечётная функция: при замене x на −x значение меняется на противоположное, то есть f(−x) = −f(x).
Линейная функция будет чётной только в случае, если k = 0, а нечётной — если b = 0. Если у линейной функции одновременно k ≠ 0 и b ≠ 0, то она не будет ни чётной, ни нечётной.
Разберём, как это работает, на примере функции f(x) = 5x. В ней коэффициент наклона k = 5, а свободный член b = 0. Сперва подставим в неё −x:
f(−x) = 5(−x) = −5x
Знак перед функцией поменялся на противоположный, а это значит, что применимо свойство f(−x) = −f(x). Следовательно, f(x) = 5x — нечётная функция.
Построение графика линейной функции
Построить график линейной функции просто. Для этого нужно найти две точки на графике и провести через них прямую. В общем виде алгоритм выглядит так.
Шаг 1. Найдём точку пересечения с осью Y. Точка пересечения с осью Y — это точка, в которой x = 0. Чтобы найти её, надо подставить x = 0 в уравнение функции y = kx + b:
y = k × 0 + b = b
Значит, у точки пересечения с осью Y координаты (0, b).
Шаг 2. Найдём вторую точку графика для любого значения x. Для этого выбираем любое значение x, желательно не слишком близкое к 0 (например x = 1 или x = −1), подставляем его в уравнение и находим значение y.
Шаг 3. Строим график. Отмечаем найденные точки на графике и проводим через них прямую — это и будет график линейной функции.
Если k = 0, то график будет горизонтальной линией, так как y = b останется неизменным при любом x.
Примеры с решениями
Разберём алгоритм построения графика линейной функции более детально. Для примера построим график возрастающей функции у = 2х + 3:
Шаг 1. Найдём точку пересечения с осью Y. Подставим в уравнение x = 0:
у(0) = 2 × 0 + 3 = 3.
Значит, координаты точки пересечения с осью Y — (0, 3).
Шаг 2. Найдём вторую точку графика. Для этого надо выбрать любое значение x и подставить его в уравнение. Возьмём х = 1 и подставим в у = 2х + 3:
у(1) = 2 × 1 + 3 = 5
Координаты второй точки графика: (1, 5).
Шаг 3. Строим график. Отметим точки с координатами (0, 3) и (1, 5) на координатной плоскости и проведём через них прямую:
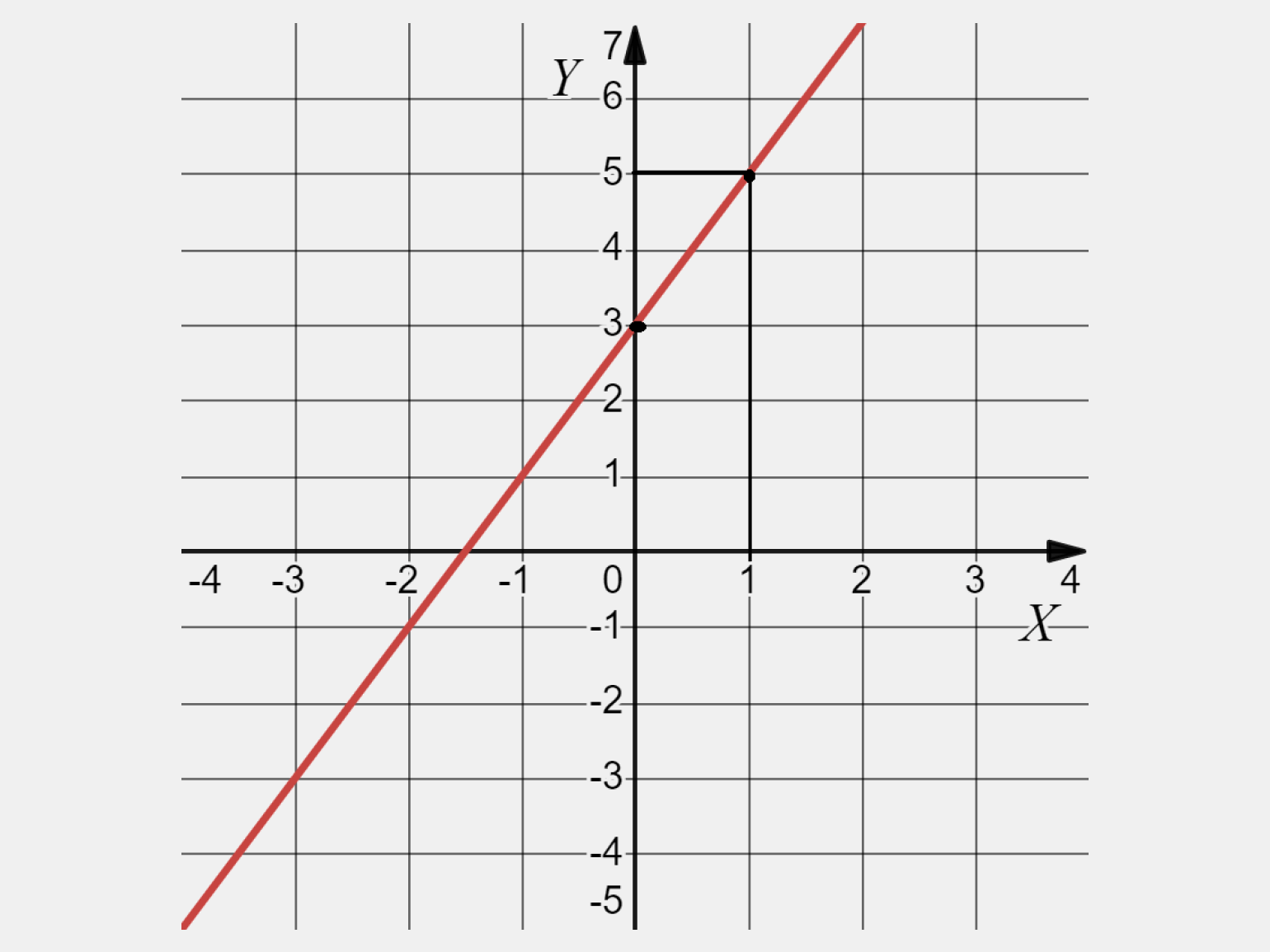
График линейной функции может быть и убывающим. Чтобы быть готовыми ко всему, разберём и такой случай.
Построим график убывающей функции у = −0,5х − 1.
Шаг 1. Найдём точку пересечения с осью Y.
y(0) = −0,5 × 0 − 1 = −1
Координаты первой точки — (0, −1).
Шаг 2. Найдём вторую точку графика.
Подставим значение x = 2 в уравнение:
у(2) = −0,5 × 2 − 1 = −2
Координаты второй точки — (2, −2).
Шаг 3. Строим график.
Отметим точки с координатами (0, −1) и (2, −2) на координатной плоскости и проведём через них прямую:
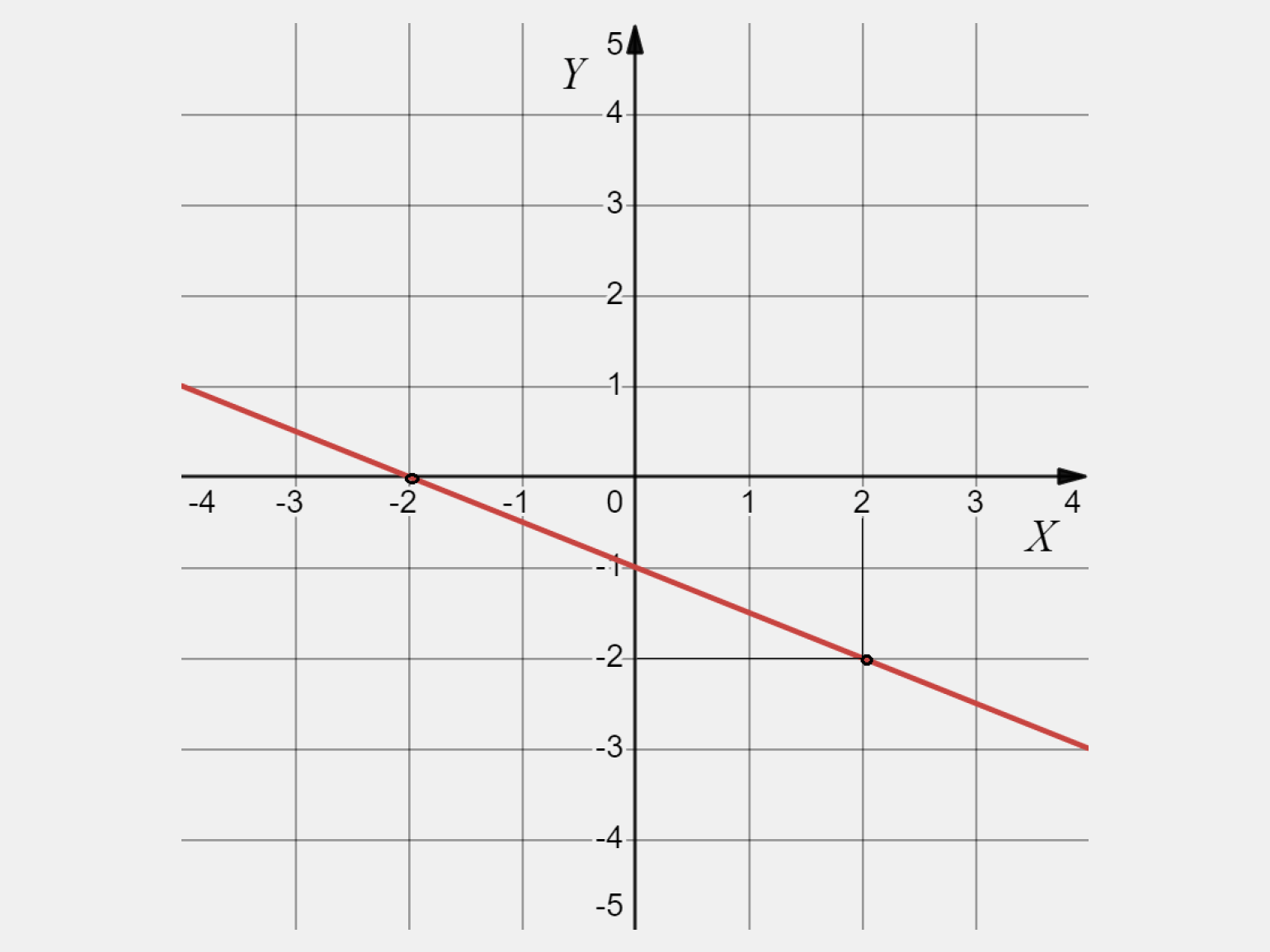
Где применяется линейная функция
Линейную функцию используют для расчёта событий и явлений, которые с течением времени изменяются равномерно. Это незаменимый инструмент для решения задач, в которых важна пропорциональная зависимость между параметрами. Ниже примеры сфер, в которых линейную функцию используют чаще всего.
Экономика и бизнес
Представьте, что вы продаёте товар с фиксированной ценой, а всего у вас есть x единиц товара. Учтём, что часть средств надо вкладывать в рекламу и продвижение. Тогда доходы от продажи товара можно описать с помощью линейной функции y = px − c.
В которой:
- y — прибыль;
- p — цена за единицу товара;
- x — количество товара;
- c — расходы на рекламу.
Физика
В физике с помощью линейной функции описывается прямолинейное равномерное движение. Если объект движется с постоянной скоростью v, то путь s зависит от времени: s = vt.
Программирование
Разработчики часто используют линейные функции для прогнозирования событий. Например, можно рассчитать, какую оценку пользователь может дать товару в онлайн-магазине. Допустим, рейтинг зависит от нескольких факторов. В таком случае формула прогноза будет выглядеть так:
y = k1x1 + k2x2
В которой:
- y — прогнозируемый рейтинг товара;
- x1, x2 — факторы, которые влияют на оценку:
- x1 — качество товара,
- x2 — цена товара.
- k1, k2 — коэффициенты значимости факторов:
- Если k1 > k2, то качество товара важнее его цены.
- Если k1 < k2, то пользователи больше внимания уделяют цене.
Что запомнить
- Линейная функция описывает прямую линию на графике, а её общее уравнение выглядит так: y = kx + b.
- За «крутизну» наклона функции отвечает угловой коэффициент k. Если он больше нуля, то график идёт вверх, если меньше — вниз. Чем больше k, тем сильнее линия «взлетает» или «падает».
- Линейная функция определена для всех действительных чисел.
- Чтобы построить график линейной функции, надо с помощью уравнения функции найти две точки, отметить их на координатной прямой и соединить их прямой линией.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!









