Как работает рекурсия функции: объясняем на примере Python

Мы уже рассказывали о рекурсии простыми словами и о том, где её можно встретить в реальной жизни. Пришло время объяснить, как и зачем в программировании применяют рекурсивные функции.

Что такое рекурсия: быстрое напоминание

В давние времена некоторые девушки, далёкие от точных наук, любили погадать, закрываясь ровно в полночь в чёрной-чёрной комнате и ставя свечку между двумя зеркалами. Согласно их поверьям, это открывало портал в потусторонний мир. А математики увидели бы в этом наглядное представление рекурсии.

В каждом зеркале отражалась свеча, и отражение этой свечи в другом зеркале, и отражение отражения, и отражение отражения отражения… и так до тех пор, пока девушке не померещится суженый.

Предупреждение: не пытайтесь повторить эксперимент! В кадре задействованы только профессиональные каскадёры! Ни одно животное в процессе съёмки не пострадало!

Выражаясь научным языком, рекурсия — это определение или изображение объекта или процесса внутри самого этого объекта или процесса.

Что такое рекурсия функции

Из вышеприведённого определения становится понятно, что рекурсивная функция — это такая функция, которая в процессе выполнения вызывает саму себя. Это свойство бывает полезно при выполнении некоторых задач в программировании.

Например, мы хотим написать функцию summa(n), которая считает сумму чисел от 1 до n. Если n = 2, то результат будет 1 + 2 = 3. Если n = 5, то получится 1 + 2 + 3 + 4 + 5 = 15. Реализовать такой алгоритм можно двумя способами: итерационным и рекурсивным.

Итерационный, или пошаговый, способ. Напишем цикл от 1 до n, в котором на каждом следующем шаге будем прибавлять к x номер шага. На языке Python это выглядит так:

def summa(n):
    x = 0
    for n in range(1, n+1):
        x += n
    return x

summa(5)
>>> 15

Рекурсивный способ. Во втором варианте нужно решить задачу, используя её же саму.

summa(5) — то же самое, что 5 + summa(4)

summa(4) — то же самое, что 4 + summa(3)

summa(3) — то же самое, что 3 + summa(2)

summa(2) — то же самое, что 2 + summa(1)

summa(1) — это 1

Получается, что мы решаем задачу, используя ответ на эту же задачу, но с меньшей величиной входных данных:

def summa(n):
    if n == 1:
        return 1
    return n + summa(n-1)

summa(5)
>>> 15

Схематично работу функции можно обозначить так:

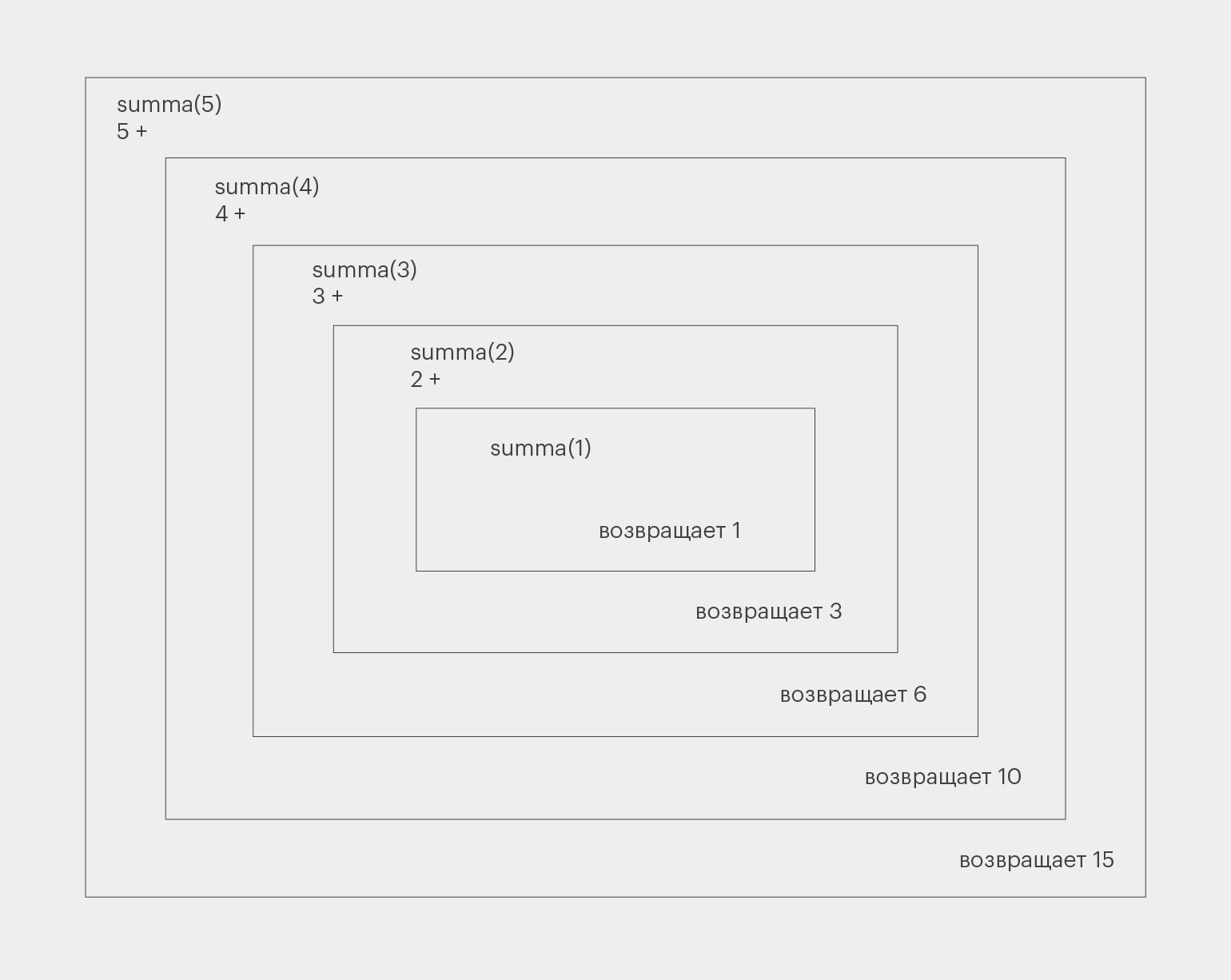
Из команд summa(n) и возвращает x можно составить лестницу. Это буквально шаги работы рекурсивного алгоритма. Сначала он постепенно уходит вглубь рекурсии — а потом идёт в обратную сторону, возвращаясь к первоначальной функции.

На самом деле в большинстве случаев рекурсивную функцию можно заменить циклами: зачастую они работают быстрее и потребляют меньше памяти.

Но при более сложных задачах лучше написать рекурсивное решение: так оперативнее, проще и понятнее, а ещё его легче поддерживать. Нередко это становится более важным и ценным, чем эффективность выполнения кода.

Условия рекурсивных алгоритмов

Вернёмся к нашему примеру с summa(n). Чтобы алгоритм работал, программа должна соответствовать двум требованиям.

Базовый случай

Помимо рекурсивного случая, когда функция вызывает сама себя ещё раз, должно быть определённое стоп-условие, чтобы этот процесс не продолжался бесконечно и функция могла завершить работу самостоятельно. В программировании это называется базовым случаем.

У нас он произойдёт, когда n станет равным 1. Мы упростили задачу настолько, что больше нет смысла считать, — и можем просто дать ответ.

Рекурсия

Чтобы прийти к базовому случаю, мы должны передавать каждой новой функции изменённые данные. Другими словами, нужно изменять аргумент функции.

В нашем коде при первом вызове n была равна 5, при втором — 4. И так до тех пор, пока n не стала равна 1. Не сделай мы этого, рекурсия никогда бы не завершилась и бесконечно порождала бы новые функции.

Как работают рекурсивные алгоритмы

В момент, когда функция вызывает сама себя, действие «материнской» функции приостанавливается — и начинается выполнение «дочерней».

Но так как рано или поздно программа должна вернуться к «материнской» функции, нужно сохранить данные о её работе. Для этого существует стек вызовов.

Разберём это на примере вызова summa(5). Представим, что компьютер хранит данные о функции в виде блока. В нём содержится значение переменной n и кусок кода, который сейчас выполняется. Пусть он выглядит так:

В момент, когда summa(5) вызывает summa(4), создаётся новый блок и кладётся поверх предыдущего:

При каждом новом вызове функции на вершине стека оказывается новый блок. Он начинает работать, остальные же в это время ничего не делают и просто хранят данные. Так происходит, пока рекурсия не доходит до базового случая:

summa(1) возвращает единицу, завершает работу и покидает стек. Теперь наверху находится summa(2):

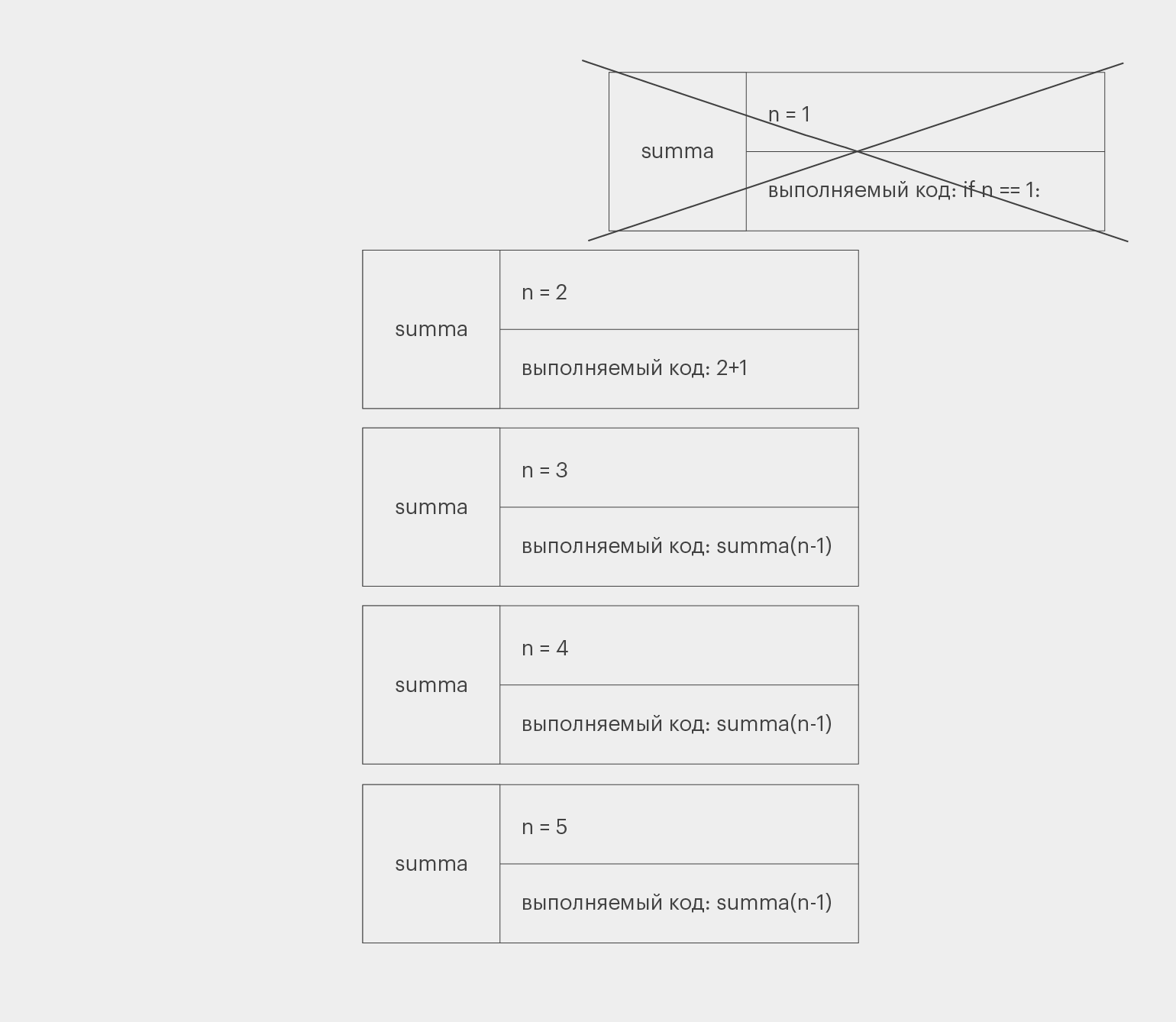
summa(2) продолжает свою работу с момента, на котором остановилась. Она заканчивает выполнять свою программу и тоже покидает стек. Теперь наверху summa(3). И так происходит с каждой функцией, пока стек не закончится.

Память и мощность любой техники ограничены, поэтому у стека всегда есть максимально допустимый размер. Например, в Python он равен 1000 вызовов. Если максимум достигнут, а мы пытаемся положить в стек ещё одну функцию, происходит ошибка «Переполнение стека».

Кстати, именно в честь этой ошибки назван популярный сайт для вопросов и ответов о программировании Stack Overflow.

Итоги

Рекурсивная функция — это функция, которая вызывает сама себя.

Для правильной работы она должна содержать базовый случай и передавать новому уровню рекурсии изменённые данные.

Информация обо всех незавершённых функциях хранится в стеке. При этом в каждый момент времени работает только та функция, которая находится наверху стека.

Рекурсивные алгоритмы обычно медленнее итерационных, но зачастую их проще писать и поддерживать.