Двоичная (бинарная) система счисления: что это и как ей пользоваться
Знакомимся с языком шифров и компьютеров — нулями и единицами.


Представьте, что вы первый человек на Земле и вам нужно что-то посчитать: предметы, расстояние, время и так далее. Это упростит жизнь, а также опишет её с помощью чисел.
Число — это какое-то количество, и его ещё нужно как-то зафиксировать. Поэтому люди придумали правило, по которому записывали числа определёнными символами — цифрами. Это правило называлось системой счисления.
Потом появились компьютеры, которые тоже работали с цифрами. Но привычную нам арабскую систему машинам «объяснить» было невозможно. На помощь пришла двоичная (бинарная) система из нулей и единиц, придуманная задолго до компьютеров.
Сегодня мы поговорим о том, какие бывают системы счисления, и сконцентрируемся на двоичной системе.
Из статьи вы узнаете:
- что такое системы счисления;
- что такое двоичная система и как ей пользоваться;
- как в двоичной системе представляются данные;
- как переводить бинарные числа в десятичные и шестнадцатеричные;
- как переводить десятичные числа в бинарные;
- что нужно запомнить.
Что такое системы счисления
Для записи числа нужен символ. Это может быть как буква β (бета) греческого алфавита, так и | (чёрточка). Главное — чтобы символ всегда означал одно и то же количество, имел то же значение. Эти символы назвали цифрами.
Система счисления — это набор цифр, каждая из которых обозначает определённое количество. Системы счисления бывают позиционные и непозиционные. Разберём это на простых примерах.
Возьмём игральные кости и попробуем описать их значения чёрточками.
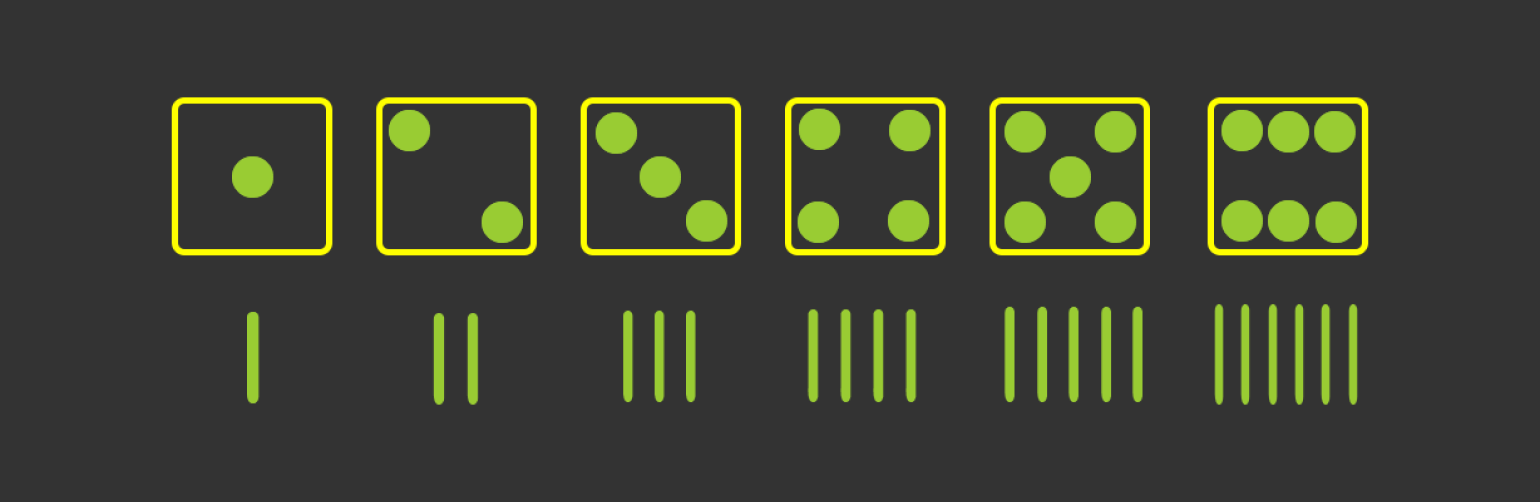
Перед нами — унарная (единичная) система счисления. Это значит, что в нашем распоряжении есть только один символ. Это не совсем удобно. Поступим по-другому: придумаем для каждого набора чёрточек свои символы.
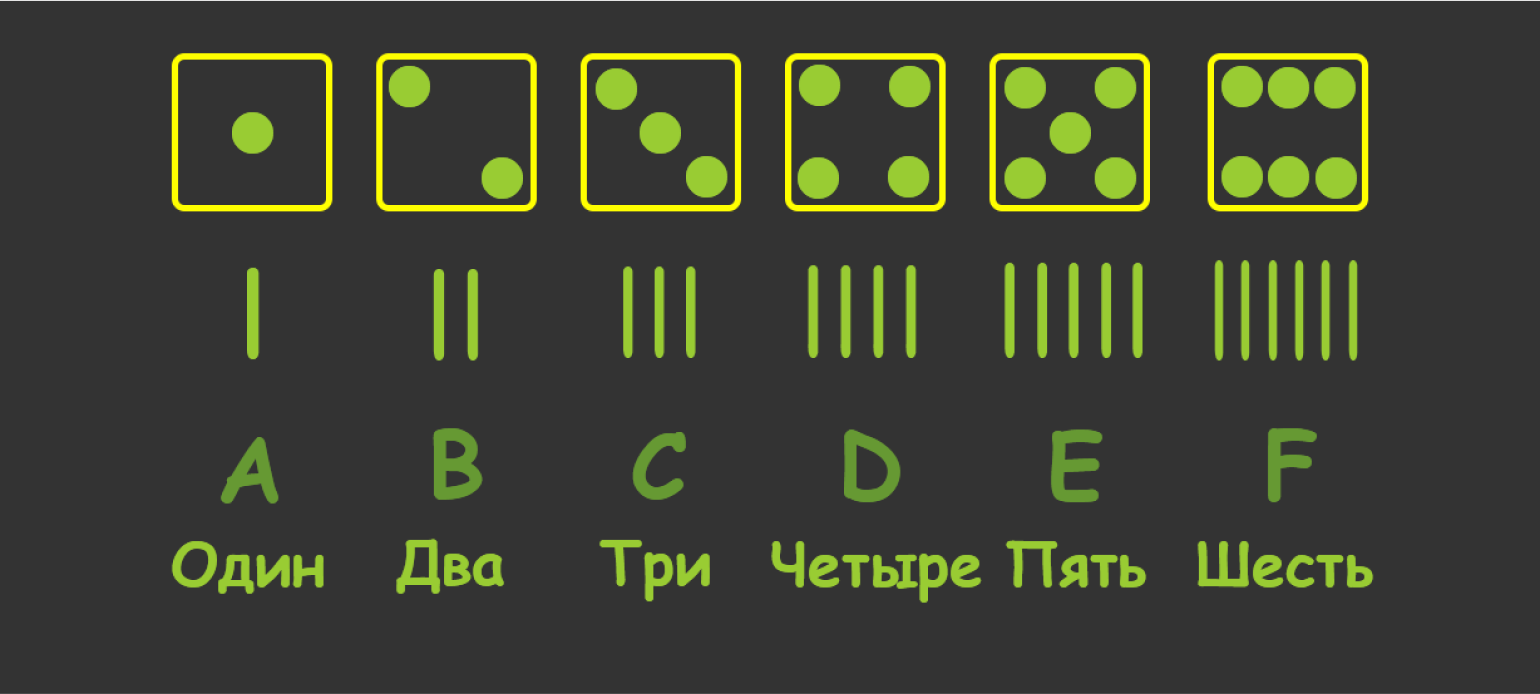
Символов теперь больше, а запись короче. Такую «кодировку» можно назвать шестеричной системой счисления, в которой 6 цифр:
- A = 1;
- B = 2;
- C = 3;
- D = 4;
- E = 5;
- F = 6.
Уже лучше, но данная система, как и единичная, — непозиционная. Это значит, что положение цифры в записи никак не связано с разрядностью (единицы, десятки, сотни, тысячи и так далее). Классический пример — римская форма записи.

Такая запись страшно затрудняет не только вычисления, но даже запись чисел, особенно больших, дробных или нерациональных — попытайтесь, например, записать «по-римски» число π (3,1415926535…).
Эту проблему решили позиционные системы счисления, самая популярная из которых — арабская. Разница — налицо. Достаточно посмотреть на запись числа 2023.

Если в первом случае поменять местами цифры M и X, значение числа не изменится — римляне считывали цифры от больших к меньшим.
Правда, у этого правила была пара исключений. Для удобства записи четвёрку записывали как IV, а девятку — как IX. Но в целом римская нумерация была непозиционной — точно так же, как древнеегипетская, греческая, вавилонская и прочие ветхозаветные.
А вот во втором случае, переставив цифры, мы получим совершенно разные результаты: 0223, 2320 и так далее.
Позиционные системы счисления имеют разряды. Их мы и меняли местами в примере выше. Разряд не может вмещать в себя число меньше или больше, чем основание системы. Основание — это количество цифр в системе счисления.

Пример позиционных систем:
| Название | Основание | Цифры |
|---|---|---|
| Двоичная (бинарная) | 2 | 0 1 |
| Восьмеричная | 8 | 0 1 2 3 4 5 6 7 |
| Десятичная | 10 | 0 1 2 3 4 5 6 7 8 9 |
| Шестнадцатеричная | 16 | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Двоичная (бинарная) система счисления
Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.
Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.
История двоичной системы счисления
В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.
В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.
Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.
В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.
В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.
В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:
- 0 — ложь — нет тока (0 бит);
- 1 — истина — есть ток (1 бит).
С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.

Читайте также:
Числа в двоичной системе счисления
Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать 0 и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.
В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Преимущества и недостатки двоичной (бинарной) системы счисления
Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:
- Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно.
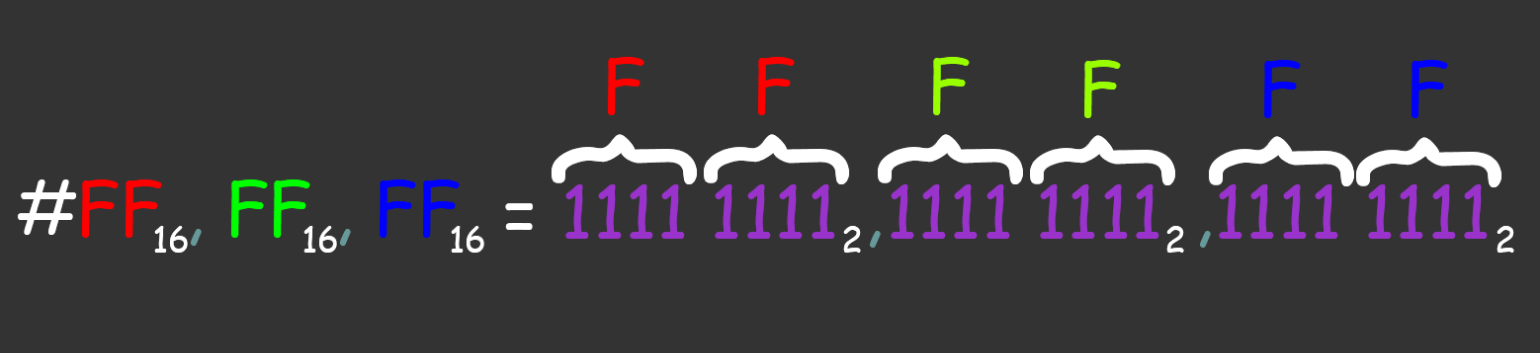
- Долгое время ручных вычислений.
- Не применяется в повседневной жизни (если, конечно, вы не компьютер).
А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:
- Позиционная система, имеет разряды.
- Применимы арифметические действия.
- Можно построить логику.
- Подходит для шифровки данных.
- Родной язык компьютерных систем.
Как в двоичной системе представляются данные
Вся информация в компьютере кодируется последовательностями битов — единиц информации, каждая из которых может принимать только одно из двух значений: 0 или 1. Именно на этой двоичной (бинарной) системе счисления построена вся сложность современного цифрового мира. Давайте разберёмся, как двоичная система применяется для кодирования различных типов информации: текста, чисел, изображений, звука и программ.
Текст. Каждой букве, цифре или знаку препинания присваивается двоичный код согласно таблице кодировки. Например, в кодировке ASCII буква A записывается как 01000001, а буква B — как 01000010. Вместе буквы AB в компьютере представлены последовательностью битов 0100000101000010.
Числа. Целые и дробные, положительные и отрицательные значения переводятся в двоичный вид по своим правилам. Например, число 13 в двоичной системе — это 1101. Отрицательные числа кодируются с помощью дополнительного кода, и −13 в 8-битном представлении записывается как 11110011. С дробными числами всё сложнее. Например, 1/3 в двоичной системе превращается в бесконечную периодическую дробь 0.010101…. Чтобы хранить такие значения, используют разные форматы с плавающей точкой.
Изображения. Картинка разбивается на маленькие точки — пиксели. У каждого пикселя свой цвет, который описывается двоичным кодом. В модели RGB цвет задаётся тремя числами в диапазоне от 0 до 255 — по одному для красного, зелёного и синего каналов. Например, чистый зелёный цвет (0, 255, 0) записывается как 00000000 11111111 00000000, а жёлтый (255, 255, 0), результат смешения красного и зелёного, — как 11111111 11111111 00000000.
Звук. Звуковая волна оцифровывается — её амплитуда измеряется много раз в секунду. Каждое измерение (семпл) записывается как двоичное число. При 16-битной разрядности каждый семпл может принимать значения от 0 до 65 535 (2¹⁶ − 1). Тишина обычно кодируется числом 32 768 (в двоичном виде 1000000000000000) — середина диапазона. Громкий звук может быть записан как 50 000 (1100001101010000), а тихий — как 20 000 (0100111000100000).
Программы. Любая программа — это набор инструкций для процессора со своим уникальным двоичным кодом. Например, в архитектуре x86 инструкция сложения двух чисел может выглядеть как 10000011 11000000 00000101 (ADD EAX, 5) — она означает «прибавить константу 5 к содержимому регистра EAX». Первый байт (10000011) — код операции сложения, второй (11000000) указывает на регистр-приёмник, третий (00000101) — число 5. Процессор декодирует эти биты и выполняет арифметическую операцию.

Читайте также:
Как перевести числа из двоичной системы в десятичную и шестнадцатеричную
Возьмём любое бинарное число, например 10102. Двоичная система счисления имеет разряды, пронумерованные справа налево.
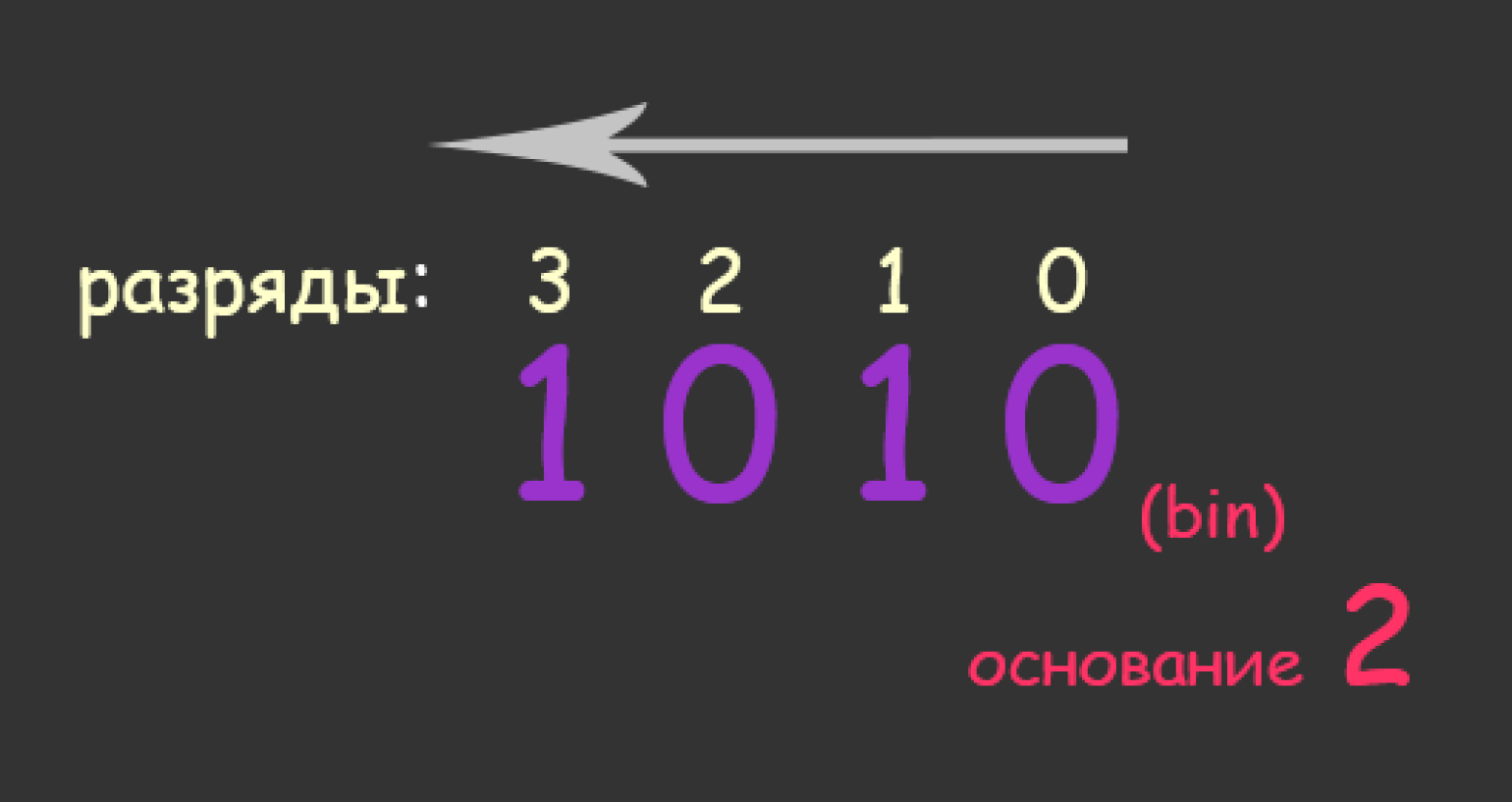
Чтобы перевести двоичное число на человеческий язык, берём цифру из наименьшего разряда, умножаем на основание 2 в степени текущего разряда. Потом переходим к следующим разрядам и всё это складываем.
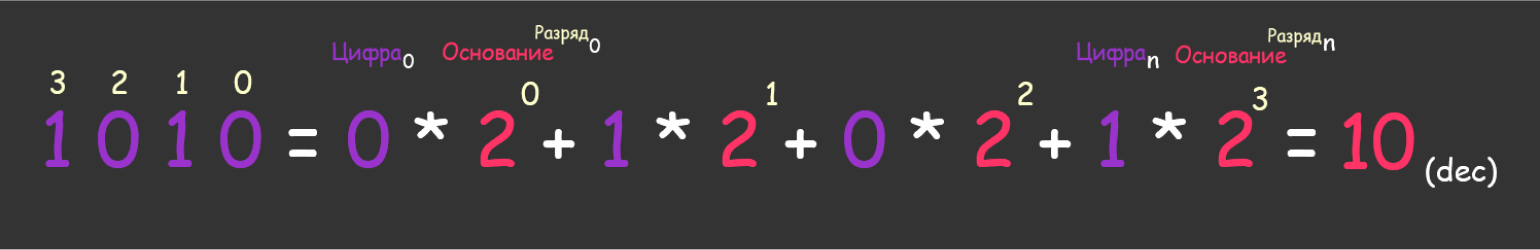
Есть метод попроще. Если в двоичном числе попадается цифра 0, сразу её вычёркиваем и складываем оставшиеся разряды.
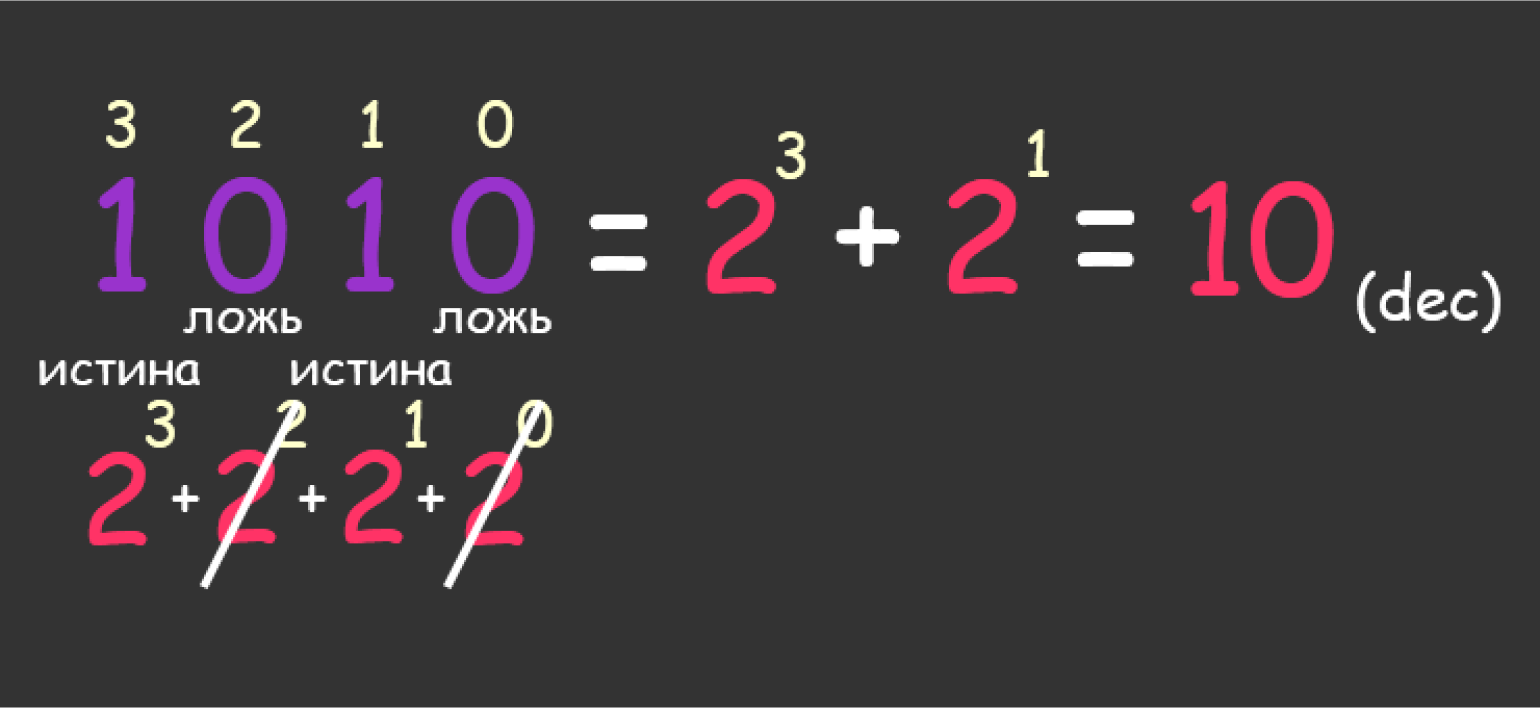
В бинарной системе счисления много интересных закономерностей. Например, посмотрите, как «перемещается» единица (бит) с ростом степени десятичной двойки.

Если взять пример из предыдущего раздела с шестнадцатеричным значением палитры RGB FF16 = 1111 11112, перевод будет выглядеть так.

Здесь мы имеем все единицы всех разрядов, а значит, складываем степени двойки от 0 до 7, и получаем такой результат.

Как перевести числа из десятичной системы в двоичную
Переведём, например, число 910 в бинарное представление. Для этого нужно столбиком разделить его на основание, то есть на 2.
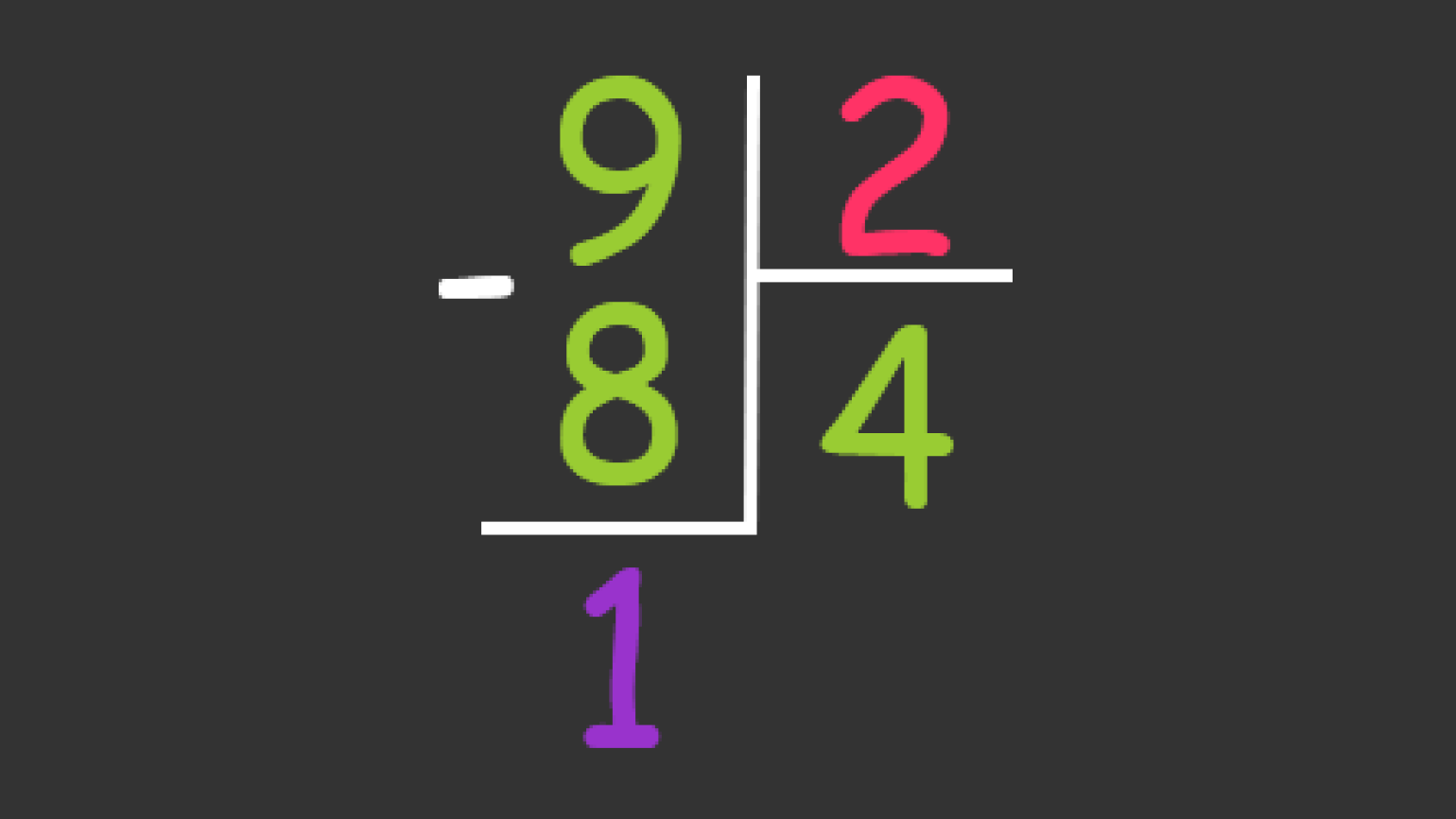
При делении любого числа на 2 в остатке всегда будет либо 0, либо 1. И этот остаток не нужно трогать, а нужно продолжать делить каждый новый результат на 2, пока не останется единица.
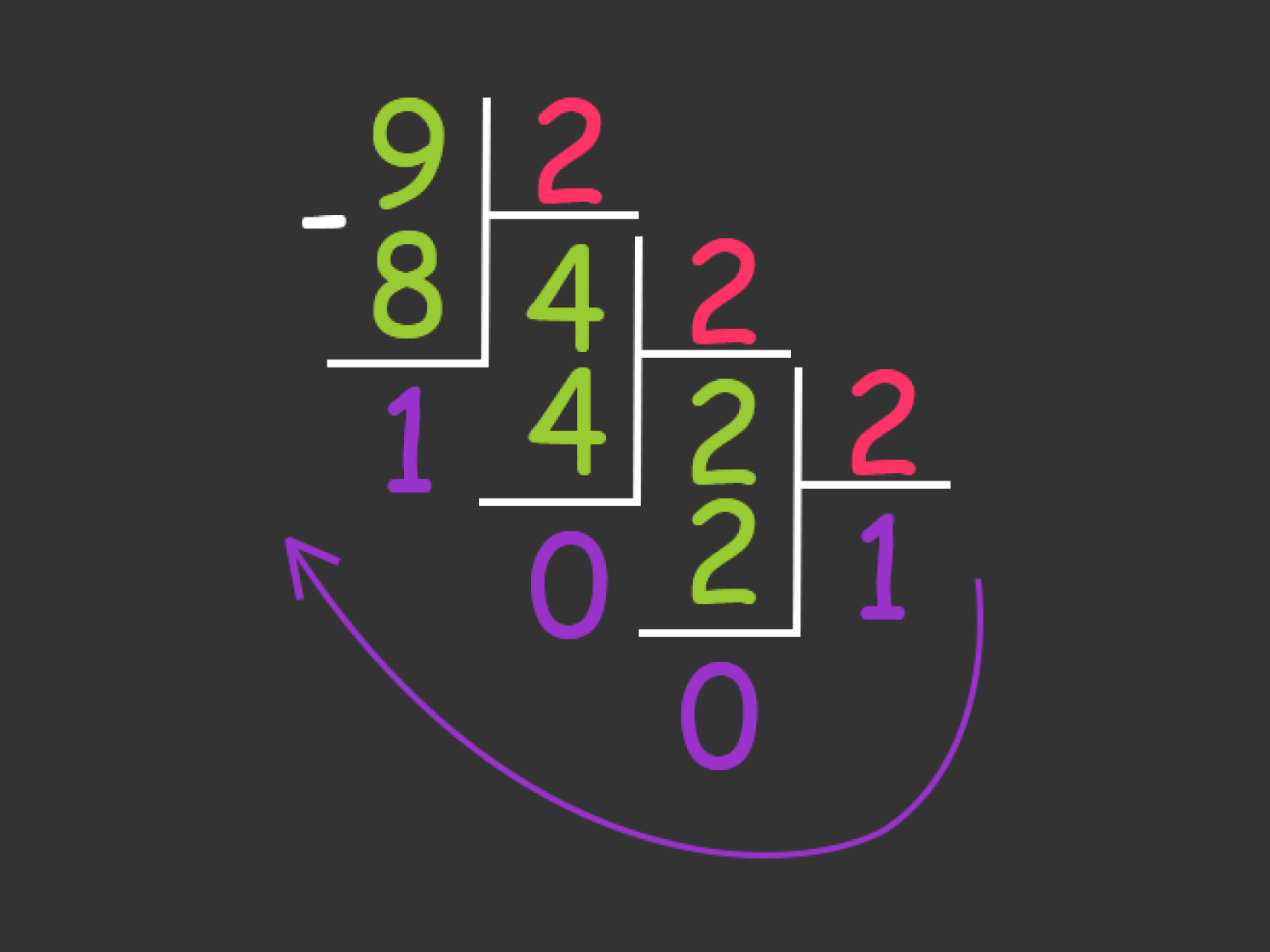
В конце эти нолики и единицы нужно собрать в обратном порядке, как показано на рисунке выше, и вы получите двоичное представление: 910 = 10012.
Подведём итоги
- Число — это количество, а цифра — символ, обозначающий это количество.
- Система счисления — набор цифр и согласованное правило описания чисел. Основание системы счисления — это количество цифр в ней.
- Разряд — это индекс цифры, который начинается с нуля и отсчитывается справа налево.
- В непозиционных системах нет разрядов и положение цифр не зависит от результата, а в позиционных строго соблюдены разряды.
- Двоичная (или бинарная) система счисления имеет лишь два значения, что отлично воспринимается любой компьютерной системой.
- Бит — единица информации в двоичной системе, 0 или 1.
Понимание концепции двоичной системы упростит взаимоотношения с компьютерными системами, а также расширит кругозор в представлении счёта.





