Что такое корреляция в статистике и как её правильно понимать
Учимся находить связи в данных и не путать их с совпадениями.


Что общего у потребления сливочного масла в США и литовских ветряных электростанций? А у мороженого и солнечных ожогов? Здравый смысл подсказывает, что почти ничего. Однако статистика утверждает, что между этими показателями есть математическая зависимость, которую называют корреляцией. Давайте с экспертом разберёмся, что это и как её посчитать.
Содержание
- Что означает корреляция
- Что такое каузальность и как она связана с корреляцией
- Для чего нужна корреляция
- Как рассчитать коэффициент корреляции

Антон Смирнов
Эксперт по анализу данных
Генеральный директор компании kongru.consulting, автор телеграм-канала «Аналитика сегодня».
Что означает корреляция
Корреляция — статистическая мера, которая отражает степень взаимосвязи между двумя переменными. Если при изменении значения одной переменной систематически меняется значение другой (увеличивается или уменьшается) и эта закономерность прослеживается на большом количестве наблюдений, то такие переменные считаются коррелирующими.
Например, корреляция существует между температурой воздуха и продажами мороженого: с повышением температуры увеличивается и объём продаж мороженого. И наоборот: в мороз мороженое почти никому не нужно.
Корреляцию можно визуально представить с помощью диаграммы рассеивания — графика, на котором данные отображаются точками в декартовой системе координат. Вертикальная ось (Y) и горизонтальная ось (X) представляют две разные переменные. Каждая точка на графике соответствует одному наблюдению, а её положение определяется значениями обеих переменных для этого конкретного наблюдения.
Ниже представлен пример диаграммы рассеивания, которая иллюстрирует зависимость тормозного пути автомобиля от скорости движения. Ось Y отражает тормозную дистанцию автомобиля, а ось X — его скорость. Каждая точка — это отдельное наблюдение, которое показывает связь между этими параметрами: чем выше и правее находится точка, тем выше была скорость автомобиля перед торможением и тем длиннее оказался его тормозной путь.
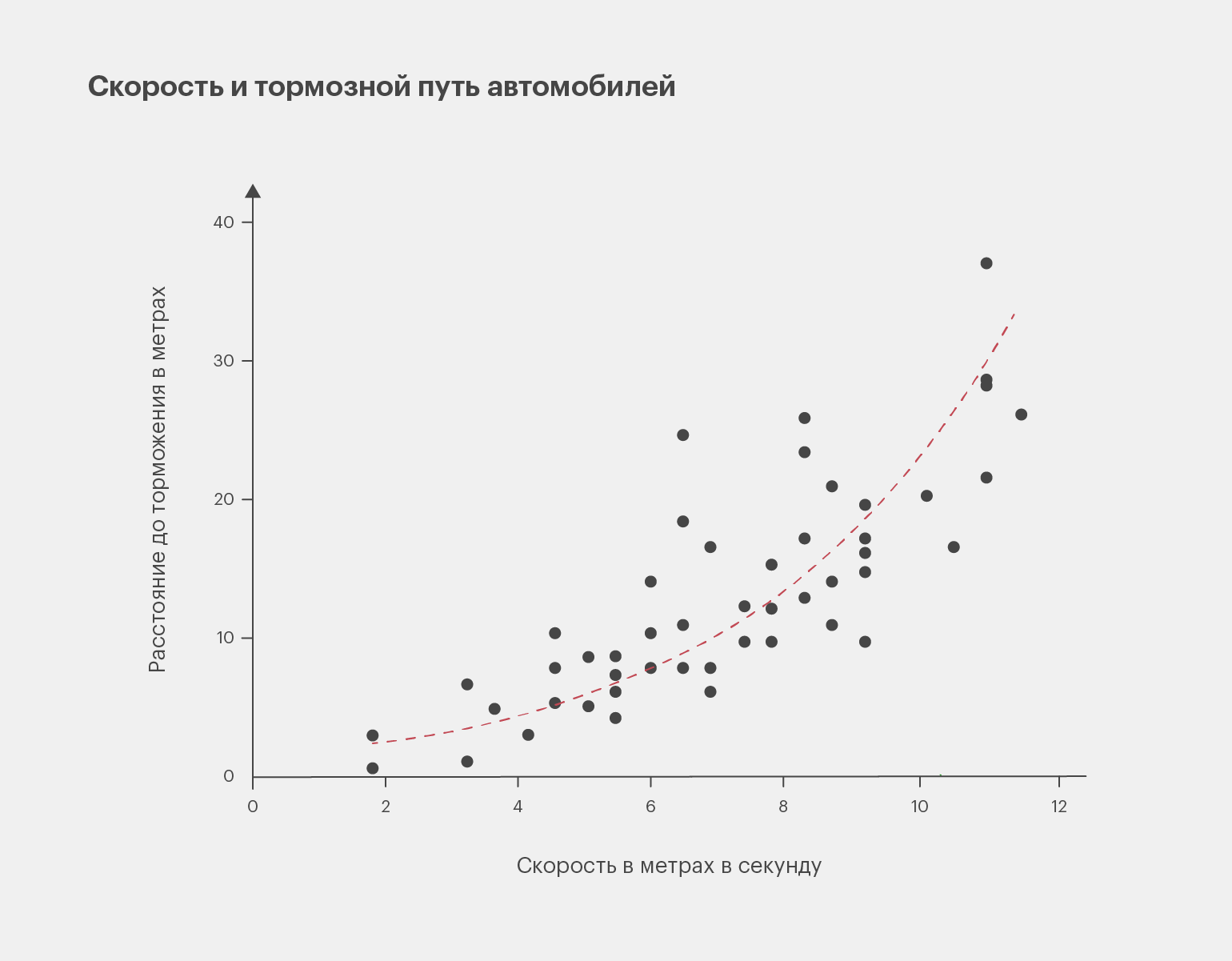
Изображение: Wikimedia Commons / Skillbox Media
Что такое каузальность и как она связана с корреляцией
В предыдущем разделе мы рассмотрели вполне логичную зависимость: чем выше скорость, тем длиннее тормозной путь. Теперь вернёмся к примеру из введения — странной корреляции между увеличением числа ветряных электростанций в Литве и ростом потребления сливочного масла в США.
Между этими двумя значениями действительно есть корреляция, и это видно на графике ниже. Чёрная линия отражает потребление масла на душу населения в США, красная — количество ветряных электростанций в Литве. Вывод напрашивается сам собой: литовские ветряки надувают масло в тарелки американцев! Звучит как кликабельный заголовок для новости.
Конечно, вы уже догадались, что это всего лишь совпадение. В статистике такое явление называют ложной корреляцией. Если анализировать тысячи различных показателей, вы неизбежно обнаружите пары переменных с сильной математической корреляцией, хотя между ними нет логической связи. В таких случаях принято считать, что между переменными нет каузальности — то есть реальной причинно-следственной связи, когда изменение одного явления непосредственно влияет на изменение другого.
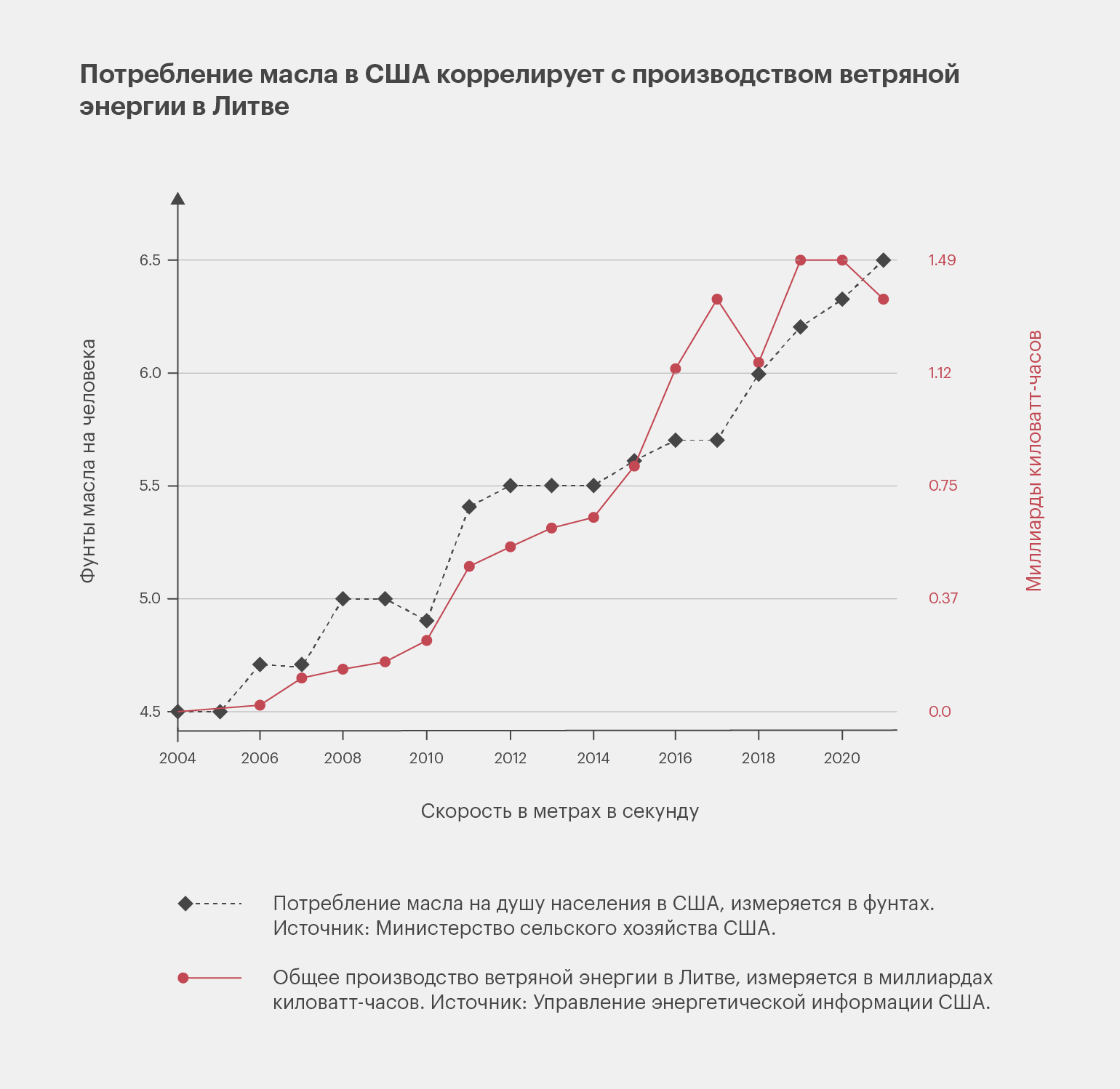
Изображение: Suspicious Correlations / Skillbox Media
Для чего нужна корреляция
Пример со сливочным маслом намеренно абсурдный. Сложности начинаются, когда отсутствие связи не столь очевидно. Например, одно из исследований показало корреляцию между наличием торговых автоматов со снеками в американских школах и уровнем детского ожирения. Вывод напрашивался сам собой: дети получают лёгкий доступ к низкокачественной и высококалорийной еде, а значит, набирают лишний вес. Следовательно, если убрать автоматы из школ, уровень ожирения должен снизиться.
Вот только оказалось, что это не так. Сразу несколько исследований показали, что наличие автоматов с джанк-фудом никак не влияет на уровень ожирения среди школьников. А значит, это всё же была корреляция, а не каузальность. Если связь оказалась ложной, то причину ожирения нужно искать в чём-то другом. Например, в домашних пищевых привычках, генетической предрасположенности или уровне физической активности.
В любом случае корреляция становится первым шагом к поиску каузальности. Когда исследователь обнаруживает статистическую взаимосвязь между двумя показателями, это даёт ему основание для более глубокого анализа: проведения экспериментов, построения моделей и тестирования гипотез. То есть у него возникает повод выяснить, существует ли между переменными причинно-следственная связь или это совпадение.
В маркетинговой аналитике корреляция встречается повсеместно. Приведу пример из практики. Представьте, что аналитик работает в компании, где заключение сделки требует множества шагов и занимает длительное время. Чтобы оптимизировать процесс, он хочет определить, как коммуникация с пользователем влияет на вероятность покупки.
Для решения этой задачи аналитик может провести корреляционный анализ, чтобы количественно оценить связь между числом взаимодействий клиента с компанией и вероятностью заключения сделки. Например, он может изучить различные типы контактов: посещения сайта, переписку по электронной почте, телефонные звонки, общение в мессенджерах и социальных сетях, а также личные встречи.
Далее на основе полученных данных аналитик может выявить статистически значимые закономерности. Например, он может обнаружить, что после 5–7 электронных писем и 2–3 звонков вероятность заключения сделки достигает максимума, а дальнейшие контакты не приносят пользы или даже могут снижать шансы на её заключение.
Зная оптимальное количество контактов для каждого сегмента клиентов, аналитик может существенно повысить эффективность маркетинговых кампаний и оптимизировать процесс продаж. Точные метрики позволяют ему выстраивать индивидуальные стратегии коммуникации для разных групп потенциальных покупателей и избегать как излишнего давления на клиента, так и недостаточного внимания к его потребностям.
Антон Смирнов, генеральный директор компании kongru.consulting
Как рассчитать коэффициент корреляции
Корреляция — это не абстрактная взаимосвязь между переменными, а вполне конкретный числовой показатель. Его можно рассчитать различными методами, и наиболее распространённый — коэффициент корреляции Пирсона (r). Этот коэффициент измеряет силу линейной зависимости между переменными и принимает значения от −1 до 1.
Линейная зависимость означает, что изменение одной переменной пропорционально изменению другой. Например, между ростом человека и его весом обычно наблюдается положительная линейная корреляция: чем выше человек, тем, как правило, больше его вес. Сила связи определяется тем, насколько абсолютное значение коэффициента |r| близко к 1. Так, коэффициент r = 0,9 указывает на сильную связь, а r = 0,3 — на слабую.
В зависимости от направления связи коэффициент корреляции может быть положительным, отрицательным или нулевым:
- Положительная корреляция (r > 0) наблюдается между количеством тренировок в неделю и результатами в марафоне: чем больше человек систематически тренируется, тем лучше его время на финише и выше позиция в итоговом рейтинге. Это прямая линейная зависимость.
- Отрицательная корреляция (r < 0) проявляется, когда увеличение одного показателя сопровождается уменьшением другого. Например, чем больше времени подросток тратит на видеоигры, тем ниже его успеваемость в школе — это уже обратная линейная зависимость.
- Нулевая корреляция (r ≈ 0) означает, что статистически значимой связи между переменными нет или она случайна. Такое может наблюдаться между ростом человека и уровнем интеллекта или между последней цифрой номера телефона и заработком. Даже при большой выборке коэффициент корреляции здесь будет стремиться к нулю.
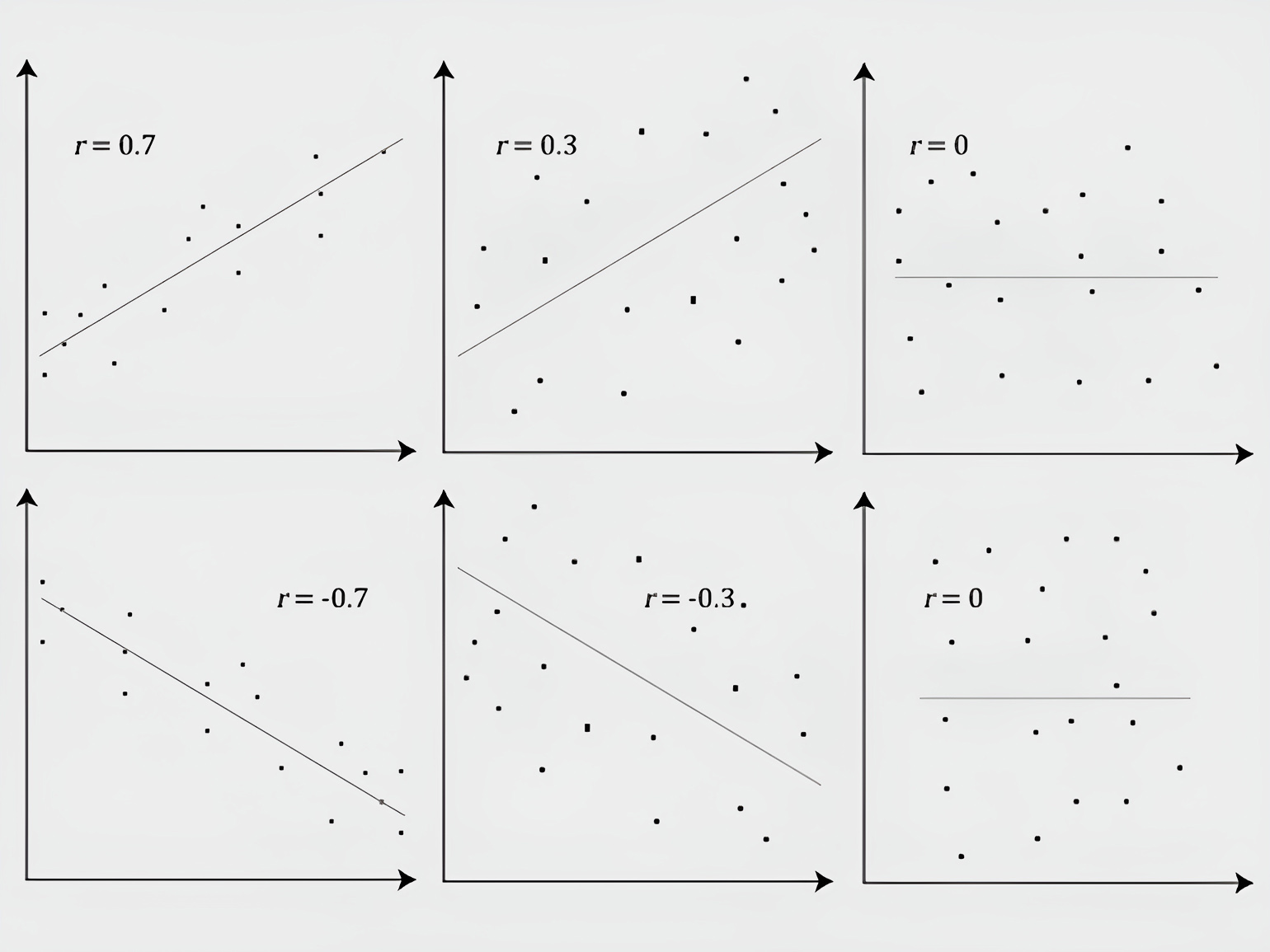
Изображение: Laerd Statistics / Wikimedia Commons
Рассчитать коэффициент Пирсона можно вручную по формуле, с помощью «Google Таблиц», Excel или языка программирования Python. Поскольку мы только знакомимся с темой, для удобства воспользуемся таблицами.
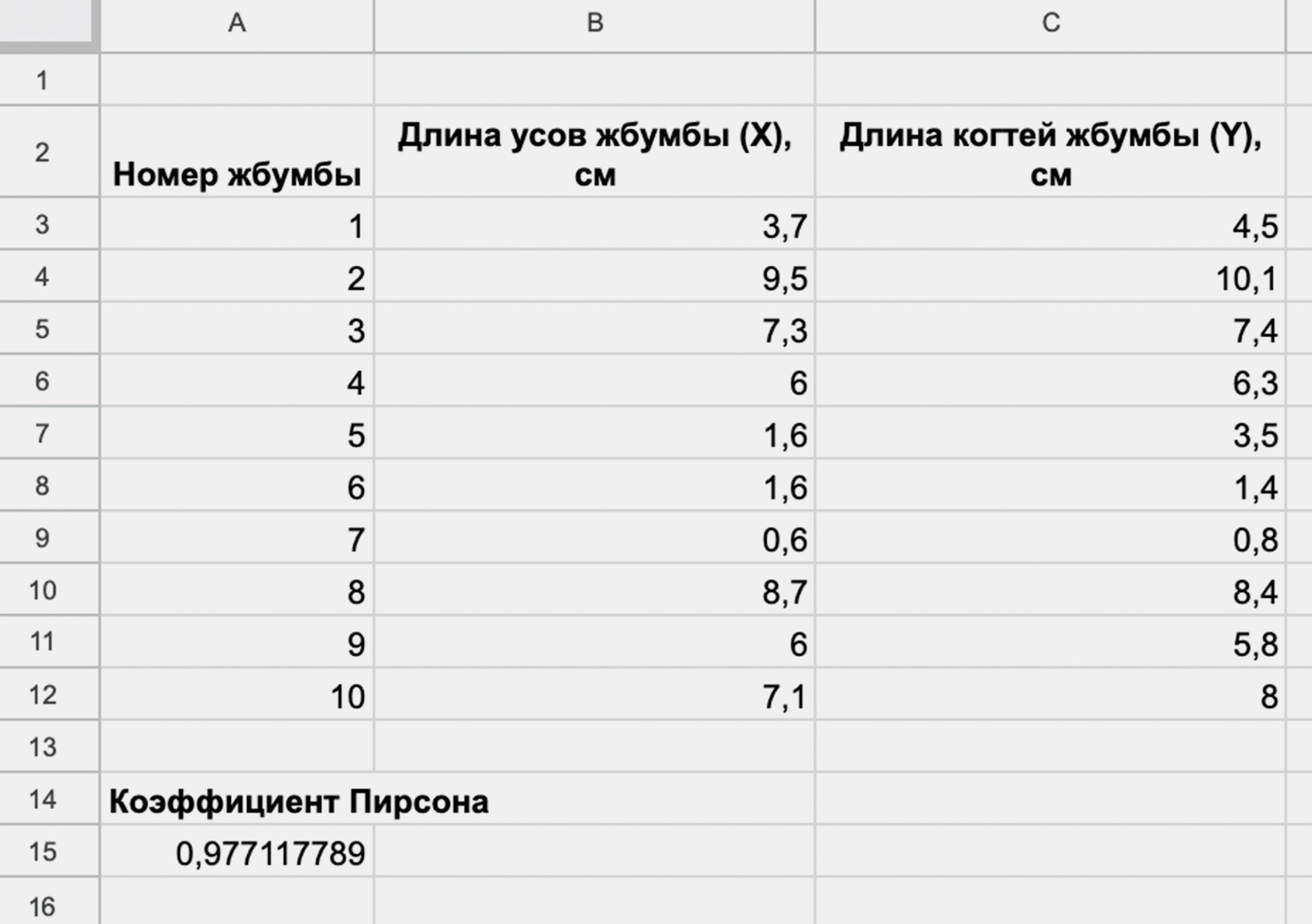
Предположим, вы хотите определить корреляцию между длиной усов и когтей вымышленного животного «жбумба». После проведения измерений вы получили результаты, которые теперь нужно внести в «Google Таблицы»:
| Номер жбумбы | Длина усов жбумбы (X), см | Длина когтей жбумбы (Y), см |
|---|---|---|
| 1 | 3,7 | 4,5 |
| 2 | 9,5 | 10,1 |
| 3 | 7,3 | 7,4 |
| 4 | 6 | 6,3 |
| 5 | 1,6 | 3,5 |
| 6 | 1,6 | 1,4 |
| 7 | 0,6 | 0,8 |
| 8 | 8,7 | 8,4 |
| 9 | 6 | 5,8 |
| 10 | 7,1 | 8 |
Выберите свободную ячейку и нажмите на значок Σ в верхней панели инструментов, чтобы открыть список функций. В подразделе статистических функций выберите PEARSON или просто введите в ячейку формулу =PEARSON. После этого выделите диапазон ячеек с первой переменной, поставьте точку с запятой и выделите диапазон со второй переменной. Затем нажмите Enter, и таблица автоматически рассчитает коэффициент Пирсона.
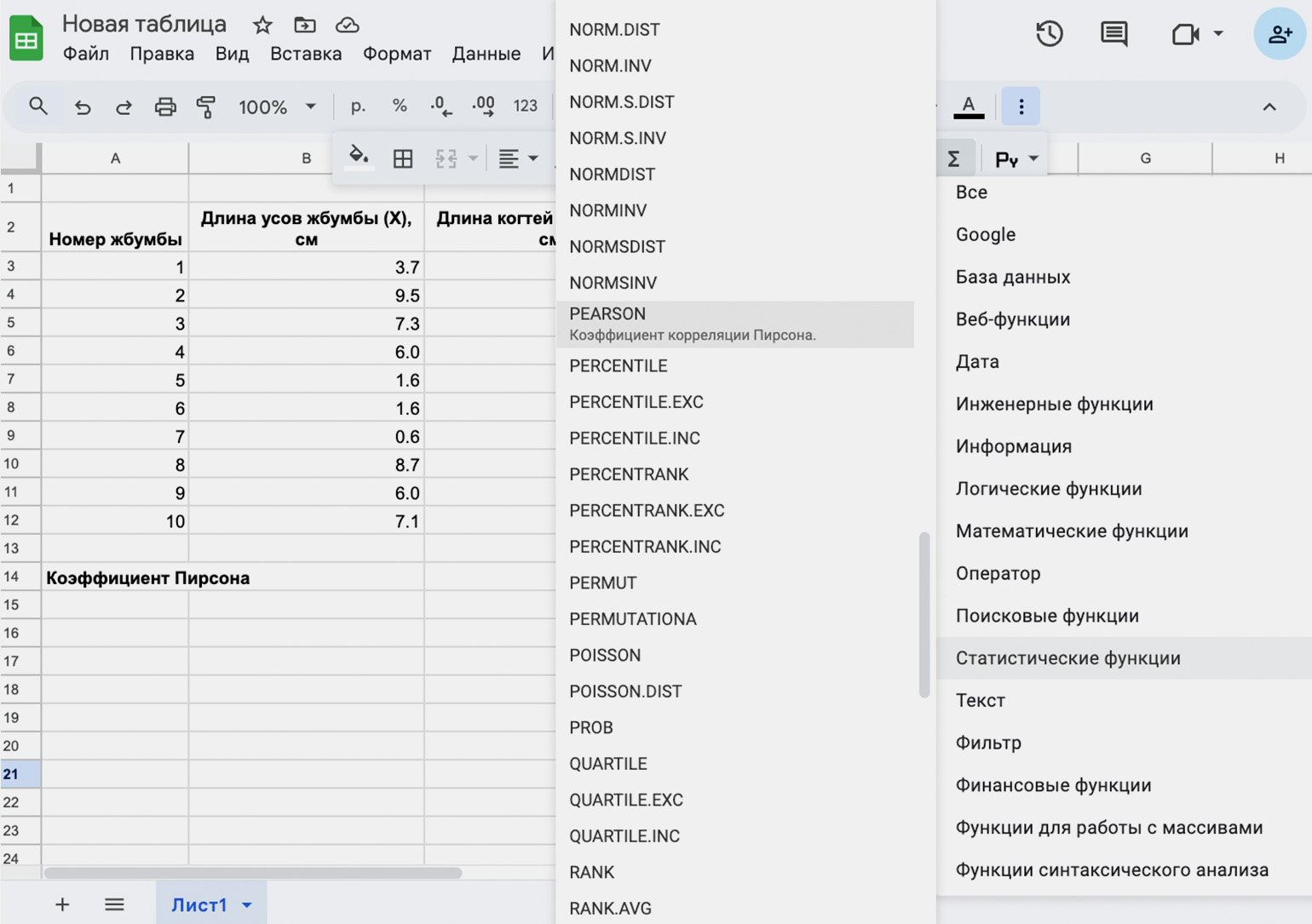
Мы выяснили, что коэффициент равен 0,97 — это очень сильная прямая корреляция. Однако из этого нельзя сделать вывод, что рост усов жбумбы вызывает рост когтей, — установить каузальность так не получится. Для этого нужны дополнительные биологические исследования. Тем не менее можно сказать, что жбумбы с длинными усами обычно имеют длинные когти.
Приведу два примера из моей практики, когда аналитики применяют коэффициент Пирсона для решения рабочих задач.
Первый случай. В компании наблюдается высокая текучка кадров, и HR-аналитик пытается выяснить её причины. Он проводит корреляционный анализ между стажем сотрудников в компании и различными их характеристиками — например, возрастом или средним стажем на предыдущих местах работы. Если коэффициент корреляции окажется достаточно высоким, то это укажет на наличие связи и поможет понять, какие факторы влияют на удержание персонала.
Второй случай. Аналитик в строительной фирме хочет проверить, как скорость возведения новых объектов зависит от типа финансирования — заёмных средств, капитала застройщика или продаж квартир на разных этапах строительства. Корреляционный анализ позволяет выявить, какой из вариантов способствует более быстрому завершению проектов.
Если коэффициент корреляции окажется низким, это указывает на слабую связь между типом финансирования и сроками возведения новых объектов. В таком случае аналитику стоит поискать другие факторы, которые влияют на сроки реализации проектов, — например, это может быть опыт подрядчиков, сезонность, погодные условия или просто бюрократия.
Антон Смирнов, генеральный директор компании kongru.consulting
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!










