Алгоритм Square & Multiply: как возводить большие числа в степень и не убить процессор
Доктор Майк Паунд рассказывает, что такое алгоритм Square & Multiply и как его используют при шифровании данных.


Майкл Паунд
Об авторе
Доктор Майкл Паунд — исследователь, работающий в Ноттингемском университете, специалист по компьютерной безопасности.
Переводчик
Марина Демидова
В видео на YouTube-канале Numberphile Мэтт Паркер проверяет, может ли очень большое число быть простым.
В одном месте Мэтт приводит такое выражение:
23373 mod 747 — число 23 возводят в степень 373 и вычисляют результат по модулю 747.
Почему это меня заинтересовало? Дело в том, что подобные вычисления используются при шифровании данных с помощью алгоритма RSA с открытым ключом. Это могут быть, например, электронные подписи или шифрование в S/MIME, TLS/SSL и других приложениях.

Кадр: Computerphile / YouTube
Этот материал — пересказ видео Майкла Паунда.
Открытый ключ состоит из двух чисел {e, n}, где e — экспонента (простое число), а n — модуль (произведение двух простых чисел). Данные шифруются следующим образом:
E = xe mod n
Здесь x — исходное значение, а E — полученный шифр. Мы возводим число x в степень e и вычисляем результат по модулю n.
Вернёмся к задаче Паркера. Такое вычисление нельзя сделать на карманном калькуляторе, и в видео на Numberphile Мэттью использует программу WolframAlpha, что разумно — я и сам часто провожу вычисления именно в этой программе.

Но мы попробуем применить алгоритм Square & Multiply (возведения в квадрат и умножения). Его можно использовать даже при вычислениях с очень большими числами.
Например, нам нужно рассчитать результат вычисления некоторого числа, возведённого в степень с показателем из 2000 бит, состоящего из 600 или более цифр, по модулю другого 2000-битного числа.
Это невероятно большие числа, и если проводить вычисления последовательно: сначала возводить исходное значение в степень, а потом вычислять результат по модулю — то это потребует больших ресурсов процессора и займёт много времени. Но с помощью алгоритма Square & Multiply время вычисления можно значительно сократить.
Напомним, что вычисление по модулю означает, что 23373 нужно последовательно делить на 747, пока остаток не будет меньше 747 (напомню, это всё числа из задачи Паркера). В итоге такая операция похожа на часы.
Вы прокручиваете стрелки до 12, а потом опять начинаете с 1, 2, 3. Но в нашем случае делений на циферблате будет намного больше.

Даже если не брать операцию с модулем, то возвести 23 в степень 373 очень сложно. Чтобы ускорить вычисление, применим алгоритм Square & Multiply.
Сначала рассмотрим его на простом примере — вычислим 28.
Мы можем произвести семь операций умножения:
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Но можно пойти другим путём:
2 × 2 = 22
(22) × (22) = 24
(24) × (24) = 28
Прекрасно — на выходе мы получили всего три операции умножения! Здесь мы возводим в квадрат не исходное число, а промежуточные значения.
Чтобы перейти к большим числам, рассмотрим механизм, который называется «квадрат слева направо».
Идея состоит в том, чтобы представить показатель степени в двоичном формате. Рассмотрим ещё один пример:
345 mod 7
Пример достаточно необычный. Сначала нужно вычислить огромное промежуточное значение 345, от которого в итоге по mod 7 получим маленькое число от 0 до 6.
Переведём показатель степени 45 в двоичную систему счисления:
101101
Теперь нам нужно определить, чему равно 3101101.
Отвлечёмся от конкретных цифр и представим, что нам нужно возвести в квадрат y1 (показатель степени записан в двоичном формате).
Получим
(y1) × (y1) = y10 (1 + 1 = 10 в двоичной системе)
Результат снова возведём в квадрат:
(y10) × (y10) = y100 (10 + 10 = 100 в двоичной системе)
Мы видим, что каждый раз, когда число возводится в квадрат, показатель степени сдвигается на один бит влево.
Умножив результат на исходное число, получим
(y100) × y = y101
Мы получили два правила:
- если число возводится в квадрат, к показателю степени слева «приписывается» 0;
- если результат умножается на исходное число, к показателю степени прибавляется 1.
Используя эти правила, мы сможем воссоздать показатель степени 101101 за минимальное количество шагов. Цифры показателя будем получать слева.
Сбоку напишем код операции:
- S (Square) — возведение в квадрат;
- M (Multiply) — умножение на исходное число.
| Код | В двоичном формате | В десятичном формате |
|---|---|---|
| S | 31 × 31 = 310 | 32 |
| S | 310 × 310 = 3100 | 34 |
| M | 3100 × 3 = 3101 | 35 |
| S | 3101 × 3101 = 31010 | 310 |
| M | 31010 × 3 = 31011 | 311 |
| S | 31011 × 31011 = 310110 | 322 |
| S | 310110 × 310110 = 3101100 | 344 |
| M | 3101100 × 3 = 3101101 | 345 |
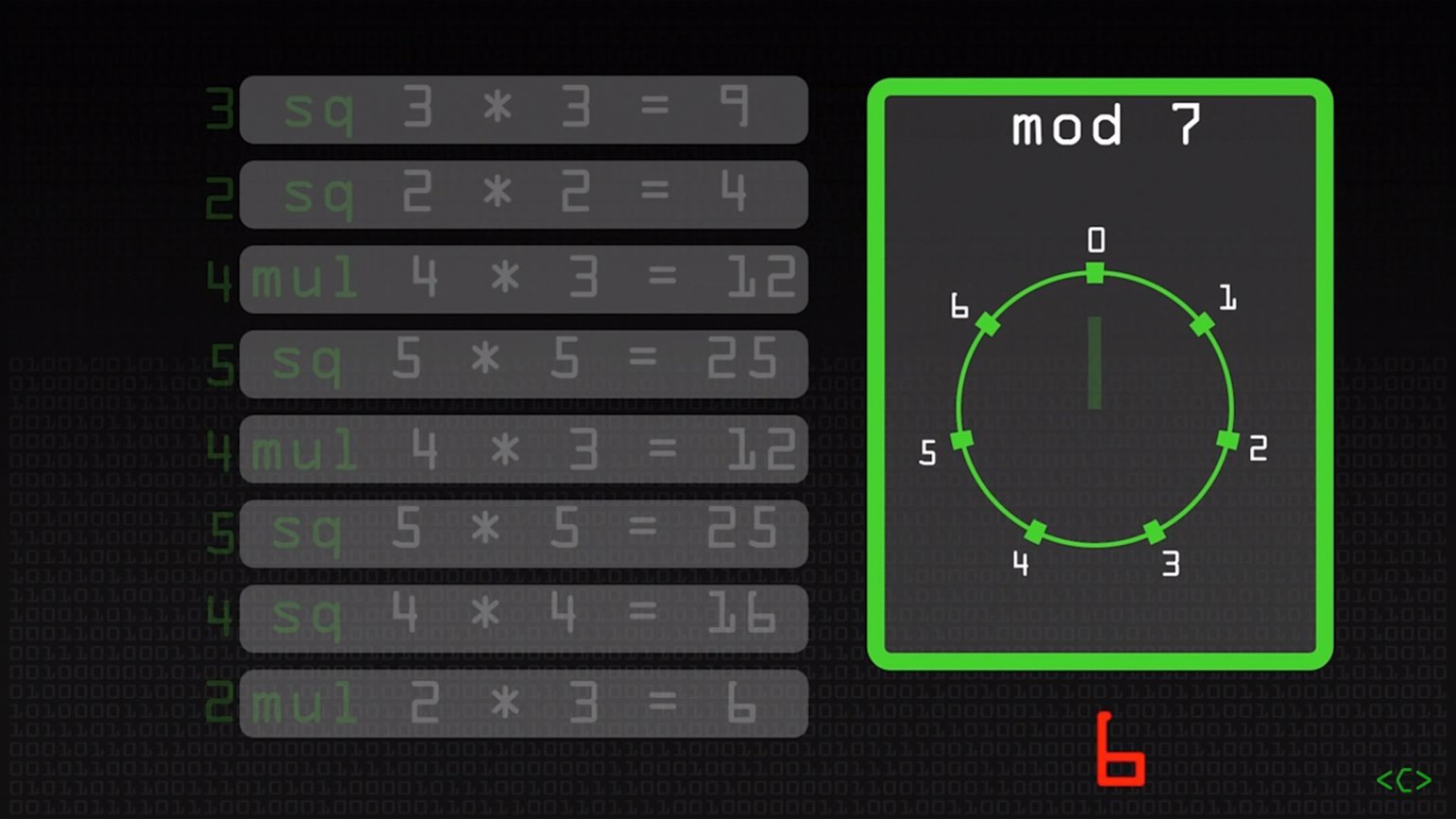
Чтобы посчитать остаток 345 mod 7, используем свойство оператора mod:
(a × b) mod n = [(a mod n) × (b mod n)] mod n
Это означает, что мы можем не вычислять результат каждой операции S или M, а найти остатки по модулю каждого сомножителя, перемножить их и применить к произведению операцию mod.
В результате получим:
| Код | В двоичном формате | mod 7 |
|---|---|---|
| S | 31 × 31 = 310 | 3 × 3 mod 7 = 2 |
| S | 310 × 310 = 3100 | 2 × 2 mod 7 = 4 |
| M | 3100 × 3 = 3101 | 4 × 3 mod 7 = 5 |
| S | 3101 × 3101 = 31010 | 5 × 5 mod 7 = 4 |
| M | 31010 × 3 = 31011 | 4 × 3 mod 7 = 5 |
| S | 31011 × 31011 = 310110 | 5 × 5 mod 7 = 4 |
| S | 310110 × 310110 = 3101100 | 4 × 4 mod 7 = 2 |
| M | 3101100 × 3 = 3101101 | 2 × 3 mod 7 = 6 |
Используя алгоритм Square & Multiply, мы легко посчитали, что 345 mod 7 = 6. Для этого нам не пришлось 45 раз перемножать тройки, чтобы вычислить огромное-огромное промежуточное число — 3 в 45-й степени. Это очень полезно для криптографии.
Вернёмся к нашему первому примеру 23373 mod 747. Показатель степени 373 в двоичном формате будет равен 101110101. Это большое число, и мы не будем применять к нему весь алгоритм Square & Multiply. Распишем коды операций возведения в квадрат и умножения.
| S | 10 | 232 |
| S | 100 | 234 |
| M | 101 | 235 |
| S | 1010 | 2310 |
| M | 1011 | 2311 |
| S | 10110 | 2322 |
| M | 10111 | 2323 |
| S | 101110 | 2346 |
| S | 1011100 | 2392 |
| M | 1011101 | 2393 |
| S | 10111010 | 23186 |
| S | 101110100 | 23372 |
| M | 101110101 | 23373 |
Если расписать, как в предыдущем примере, все операции S и M и вычислить результаты по mod 747 (без калькулятора здесь не обойтись), то конечный результат будет равен 131.
Количество операций здесь — 13. Мы видим, что оно зависит от показателя степени. Для каждого нуля промежуточное значение возводится в квадрат, а для единицы — возводится в квадрат и умножается на исходное значение. Получается, чем больше единиц, тем больше операций.
Теперь рассмотрим простое число 65537. Его используют в качестве экспоненты в открытых ключах большинства сертификатов RSA. Например, когда сервер выдаёт вам сертификат, открытый ключ обычно состоит из числа 65537 и какого-то полупростого числа n.
Почему так? Дело в том, что 65537 — это число Ферма, которое можно представить как 216 + 1. В двоичной системе счисления оно равно:
100000000000000001 (две единицы, а между ними 16 нулей).
При проверке электронной подписи, помимо проверки заполнения и множества других вещей, компьютер вычисляет какое-то сообщение, или его хеш, или его представление в таком виде:
h(m)65537
Вычисление будет выполняться достаточно быстро, так как в двоичном представлении числа 65537 почти нет единиц. Вычисляется множество квадратов, и только в конце производится одно умножение. Подобная проверка осуществляется каждый раз, когда вы заходите на веб-сайт.
Но здесь я хочу добавить, что скорость проверки зависит не только от открытого, но и от закрытого ключа, который в RSA используется для расшифровки данных. А в нём количество нулей и единиц может быть каким угодно. Тем не менее использование числа 65537 в открытом ключе ускоряет вычисление и экономит ресурсы компьютеров.










