Математическое мышление: что это и как его развивать
Поговорили об этом с исследовательницей математического образования, серьёзно погружённой в тему.



Анна Шварц
Профессор-ассистент Университета Утрехта (Нидерланды). Кандидат психологических наук. Диссертацию в МГУ имени М. В. Ломоносова защищала по теме «Роль чувственных представлений в овладении математическими понятиями». Разработала курс по математике для начальной школы в «Учи.ру», консультировала разработку заданий «Яндекс Учебника».
Что такое математическое мышление
— Что означает термин «математическое мышление»?
— Есть разные определения. Дело в том, что эту тему — то, как человек мыслит в области математики, — изучают как минимум два научных направления. Первое — когнитивная наука, занятая исследованиями процессов познания. Второе — наука о математическом образовании. Так как это разные научные сообщества с разными подходами, понимание математического мышления у них различается.
Я бы определяла этот термин как мышление в рамках культурной практики математики. Речь о том, что в различных областях деятельности сложились свои культурные практики, и они отличаются по принятым в них стратегиям мышления.
То есть мышление — включая планирование, рассуждение, обоснование — в физике, географии, математике, а также в танце или живописи строится по-разному, потому что это разные культурные практики.
— Но есть и другой подход к понятию математического мышления?
— Да, так как математика — очень широкая культурная практика. Скажем там, она стоит очень высоко в традиционной иерархии возможных человеческих деятельностей и наук. Это можно, например, заметить по разности зарплат в профессиях, требующих и не требующих математической подготовки. Соответственно, математика занимает очень большое место в школьной программе, и сообщество пытается «раздуть» это направление.
Говорят, что математическое мышление — нечто фундаментальное, связанное с логикой, связанное с умением рассуждать.
И из-за этого, наверное, возникает ощущение, что математическое мышление — нечто самостоятельное, что его можно развивать в целом, независимо от математики, от предмета, а также ожидание, что его развитие повлияет на другие области жизни.
— А какое понимание сейчас больше распространено в науке?
— В отечественной психологии долгое время был тренд на широкое определение. Математическое мышление связывали с умением рассуждать в целом, с логическим мышлением.
В западной науке сейчас стремятся рассматривать обучение математике в контексте обучения другим дисциплинам, в рамках STEM (так называют предметы в области естественных наук, технологий и математики). Более того, психологи образования говорят о необходимости рассматривать мышление в области математики в контексте решения жизненных задач.
Долгое время на математику смотрели иначе: в течение XX века произошло её отделение от жизненного мира. Упор в подготовке математиков, например в рамках олимпиадного движения, делали на тренировку специфических навыков, которые зачастую оказываются неприменимы к решениям жизненных задач.
В итоге математика становилась предметом не для многих, для избранных. А сейчас происходит попытка пересмотреть подходы к обучению. Этот тренд заметен и в больших международных исследованиях уровня образования школьников разных стран PISA и TIMSS.
Как развивать математическое мышление
— Изучение математики в школах в основном состоит из освоения чётких правил, понятий, приёмов решения задач. Этого достаточно, чтобы развивалось математическое мышление?
— Традиционно математические задачи делятся на рутинные и творческие. Рутинные задачи обладают заранее известным набором действий. Чтобы их решить, нужно определить тип задачи и действовать по заданному алгоритму.
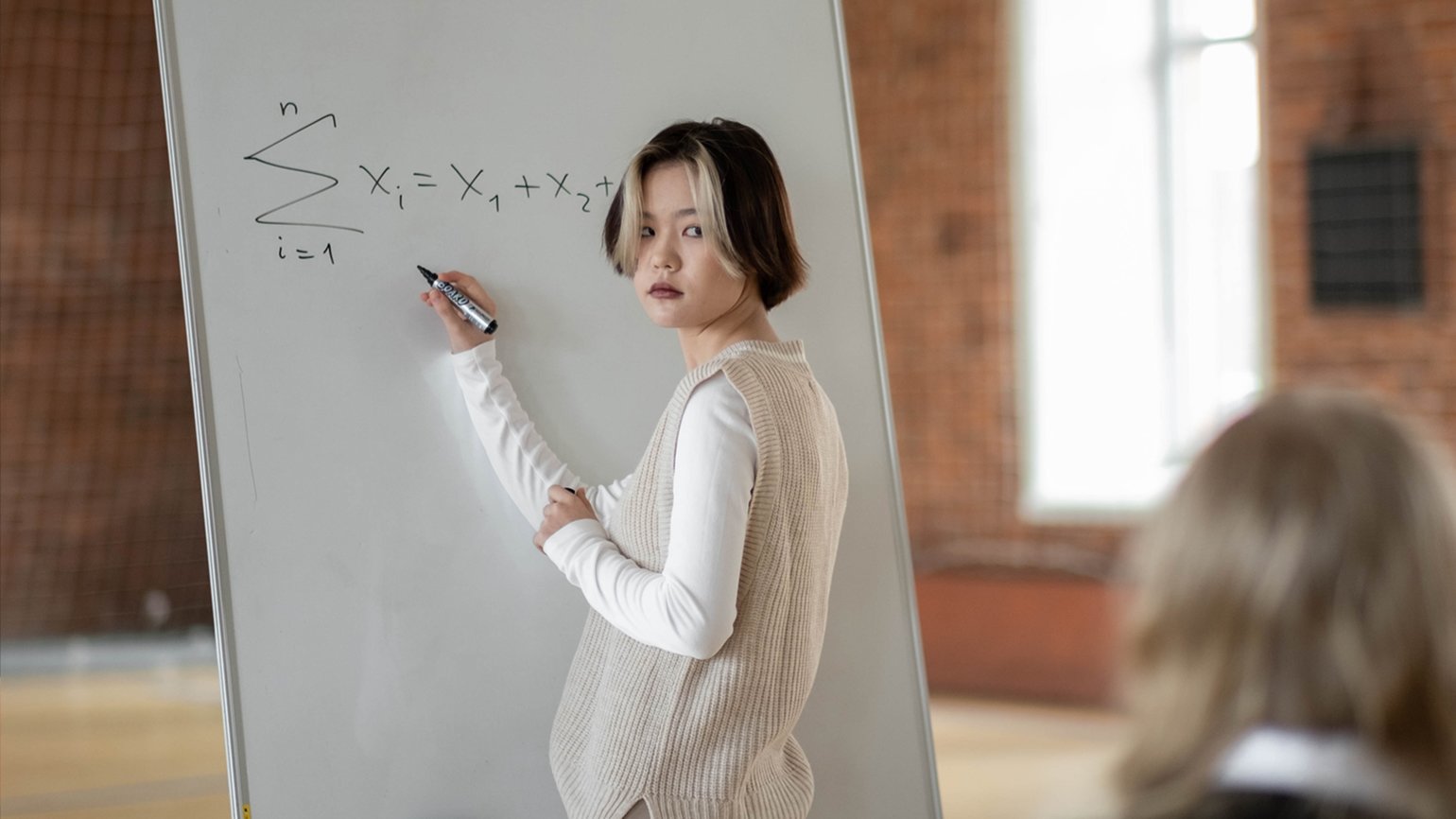
К сожалению, школьные программы во всём мире в большей степени построены на освоении таких рутинных задач. Но эти навыки едва ли можно назвать мышлением. Потому что мышление — это поиск решения без заранее известного алгоритма. А выученные действия по правилам я бы вообще не относила к математическому мышлению.
— А когда начинается математическое мышление?
— Тогда, когда действительно используются математические понятия. Но тут есть отдельный большой вопрос: а что такое математическое понятие?
Во-первых, оно задаётся не только определением. Например, понятие тригонометрической функции включает в себя комплекс различных моделей — и алгебраическое выражение, и представление через треугольник, и через единичную окружность, и через графики. И чтобы понять, что такое тригонометрические функции, и использовать их в математическом мышлении, нужно освоить сложный комплекс действий с разными объектами.
Причём если формальные операции могут быть записаны алгоритмически и выучены, то овладение визуальными моделями — это не то чтобы искусство, но некоторая плохо формализуемая практика, которой нужно учиться через пробы и ошибки. Как, например, дети учатся пользоваться вилкой и ножом и ездить на велосипеде. Нельзя сразу освоить практику, прочитав об этом в книжке.
Во-вторых, выученное определение или алгоритм сами по себе мало что дают. Потому что «выучил» ещё не значит «овладел» или «может применить». Есть феномен вербализма, когда ученик может выдать определение, но опознать обозначенный в нём объект не может. Например, точно знает, что прямоугольный треугольник — это треугольник с прямым углом. Но когда видит на картинке прямой угол в непривычном положении, то не понимает, что это за треугольник. Таким образом, знание определений, знание свойств и правил ещё не даёт возможности мышления.
— А разве умение решать творческие задачи, то есть мыслить в области математики может появиться без освоения алгоритмов и правил? И какое должно быть соотношение рутинных и нерутинных задач, на ваш взгляд, в школьной программе?
— Конечно, должна быть некоторая база, которую нужно в каком-то смысле отточить. Дети должны свободно считать в пределах ста, свободно пользоваться таблицей умножения — просто потому, что это является пререквизитом для освоения более глубоких моментов.
Но, к сожалению, традиционные подходы к оттачиванию этой базы не дают гибкости, которая нужна в решении последующих задач. Например, при заучивании таблицы умножения ребёнок запоминает «шесть на восемь — сорок восемь». А чтобы хорошо решать задачки, которые будут включать в себя этот числовой материал, нужно понимать, что 48 можно представить и как 12 на 4, и как другие возможные произведения.
То есть нужна некоторая «напитанность», насыщенность этим числовым материалом, а не просто выучивание. Мы могли бы перенести сюда такое понятие, как ловкость. Ловкость движения — ловкость счёта. Это понимание, что считать можно разными способами, выбирая наиболее удобный в данной конкретной ситуации. То есть даже базу надо оттачивать не как набор алгоритмов, а как гибкий навык.
— То есть тренировка, повторение каких-то простых действий нужны, но не в такой форме, как это привычно?
— Да, тренировка нужна, но через гибкость и через решение задачек, а не просто зазубривание.
И есть второй аспект, о котором я хочу сказать. Есть привычка видеть мир математически — я могу оценить, сколько воды использую в течение дня, рассчитать длительность какого-нибудь путешествия, определить оптимальный маршрут похода за покупками с точки зрения стоимости и временных затрат. Все эти бытовые задачки принципиально нерутинные и непошаговые.
И в тот момент, когда мы начинаем учить детей пошаговым алгоритмам, это умение замечать моменты, где математическая практика может помочь, к сожалению, разваливается или просто не формируется. Поэтому, в частности, говорят о том, что есть school mathematics and street mathematics — школьная математика и уличная математика.
— И человек, который владеет уличной математикой, может не владеть школьной?
— Да, это много исследовали, особенно в Индии. Там дети торгуют на улицах и прекрасно справляются с числовыми предметами и примерами в своей ежедневной практике счёта. А на школьной скамье они оказываются совершенно беспомощны, у них просто не проходит связь между тем, что им реально нужно для жизни, и тем, что им дают в школе в виде «сделай А, сделай B, сделай С».
В какой-то момент в 1990-е даже стали говорить, что переноса знаний и навыков не существует, что это придуманное психологами понятие. Потому что для переноса способа рассуждения со знакомых условий на новые ребёнок должен сначала опознать ситуации как похожие. А опознание школьной ситуации в тетрадке и жизненной ситуации в мире как похожих практически нереалистично — они совсем не похожи, если на них невооружённым взглядом посмотреть.

Подробнее о переносе знаний и умений из одной области в другую читайте здесь:
Когнитивная психология: что она изучает и почему важна для сферы образования
— Но почему же некоторые дети готовы решать такие задачи, которых они никогда не видели? Дело в их врождённых способностях?
— Насколько я знаю, психогенетические исследования показывают, что есть определённые факторы наследуемости. Но такие исследования, как правило, плохо учитывают взаимодействие генетики и среды. Дело в том, что если и есть какие-то «математические гены», то ребёнок, который с ними родился, ещё и растёт в семье, где родителям свойственно, например, его спрашивать: «А нам нормально посчитали сдачу в магазине?» Или: «Как ты думаешь, хватит этих 100 рублей, чтобы мороженое и черешню купить?» Получается, среда и генетика настолько тесно взаимосвязаны, что сказать, что врождённо, а что идёт из семейных практик, крайне сложно.
То есть как человек, работающий в образовании, я бы не стала задумываться над вопросом о врождённости. Мнение, что способности определяются генетически, снимает с нас как с учительского сообщества ответственность, что мне кажется неправильным. Любой ребёнок может научиться очень многому, если к тому есть подходящая среда.
— А если в дошкольном возрасте способности ребёнка вот так развивали в подходящей среде, это значит, что в школе с математикой он будет легко справляться?
— Фундаментальный фактор тут, мне кажется, — это мотивация. Когда маленький ребёнок осваивает счёт и, например, помогая накрыть стол, считает, сколько нужно вилок и ложек для всех гостей, ему это приятно и радостно. Ещё и потому, что это вызывает положительные эмоции родственников, и в результате формируется мотивация, которая способствует освоению математических навыков.
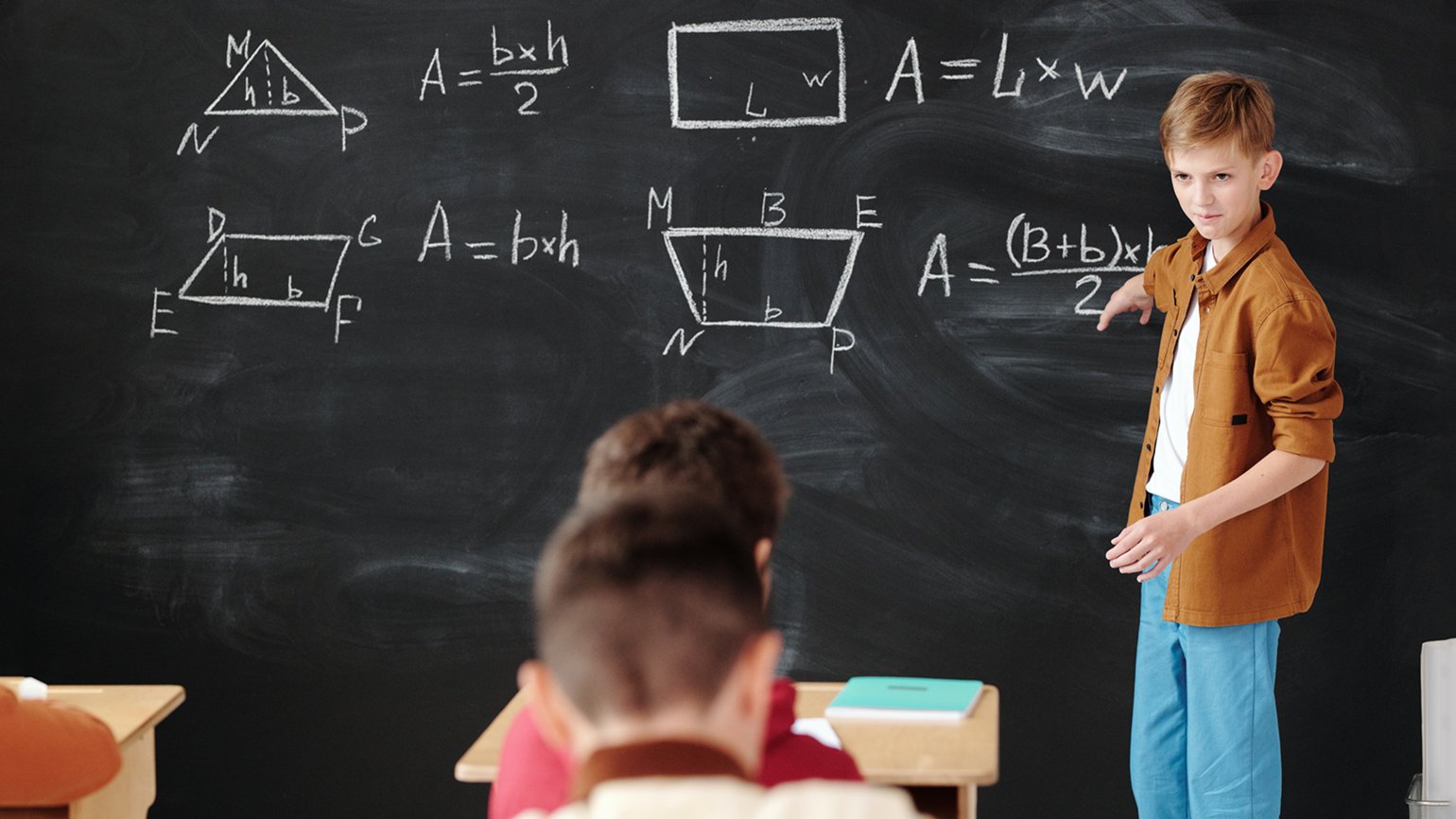
Но что происходит в школе? Мы в своё время в «Учи.ру» много анализировали программы начальной школы и вот что поняли. Допустим, приходит в первый класс ребёнок, который уже неплохо считает до десяти, а то и до 20. И его начинают снова учить считать до десяти.
Так он сидит полгода, а то и год, и понимает, что на математике не происходит ничего, ему дико скучно. Во втором классе начинает что-то происходить, но оно, в общем, тоже очень всё простое и даётся, как правило, без большого труда. А дальше вдруг происходит совершенно радикальный разрыв. Задачки, которые появляются в школьной программе в конце третьего и в четвёртом классе, на порядок сложнее. И в этот момент мы теряем для математики огромное количество детей.
То есть многим школьникам оказывается просто невозможно сделать этот скачок. А естественной мотивации и готовности преодолевать математические трудности к этому моменту у них уже нет — всё любопытство, которое было, убито скукой на уроках прошлых лет.
Что делать, если отношения с математикой не сложились
— Получается, вот этот скачок в сложности задач — одна из причин, почему так много людей уже в школе убеждаются, что они якобы не способны ни к какой математике?
— Отношение к математике школьников вообще одно из наиболее категоричных среди всех предметов: есть исследования, что 20% детей её любят, а 80% ненавидят. То есть никто не относится спокойно, что-то есть в математике такое, что заставляет к ней отнестись очень специфическим образом.
Как мне кажется, большую роль тут играет своего рода привилегированная позиция математики. Опять же, если мы просто возьмём корреляцию зарплат с уровнем математической подготовки, она будет совершенно феерической. То есть люди с математической подготовкой будут получать в разы больше. И, соответственно, на ребёнка уже с начальной школы оказывается давление, что математика — это так важно, математика — это такой особенный предмет. Это может и вызывать негативное отношение в дальнейшем.
— Как на это давление, с вашей точки зрения, влияет популярность информационных технологий, IT-профессий сейчас?
— Это я вижу скорее как позитивный момент, потому что чтобы обучиться IT-профессиям и программированию на достаточном уровне, не всегда нужно высокое знание математики. В некотором смысле это открывает широкие возможности и для взрослых.
Плюс есть довольно много очень хороших детских курсов программирования, которые как раз в силу своей новизны не подвержены традиционалистскому, рутинному, алгоритмическому способу подачи материала, а построены больше на детском любопытстве и возможности открывать и исследовать.
Для ребят программирование зачастую отвечает их жизненным задачам, включая игровые: например, они играют в Minecraft и что-то немного хотят улучшить для себя. Это можно решить несложным программированием. А это именно то, о чём мы говорили в начале: образование встраивается в жизненный мир. И интерес к программированию может удовлетворить взрослых и снять напряжение с математики.
— Можно ли как-то встроить математику в свою жизнь во взрослом возрасте?
— С одной стороны, давление «ты должен это знать» становится гораздо меньше с возрастом, и за счёт этого взрослые тоже могут разобраться.
Но с другой стороны, порог входа в математику довольно-таки высокий. Если ты в школе не учил историю, а потом вырос и подумал: «Неплохо бы мне историю знать» — то это не так уж трудно наверстать. Надо, конечно, приложить усилия, время, послушать, разобраться, запомнить — но каких-то новых навыков для этого, по большому счёту, не требуется.

А в математике нужно преодолеть уровень свободного владения числовым материалом, алгебраическими формулами, визуализацией. Как мы говорили, это похоже на умение кататься на велосипеде или на коньках — навык, который должен «встать». И встать он не может без тренировки и практики. Соответственно, за счёт этого освоить на реально хорошем уровне математику взрослым оказывается не так легко.
— Как вы считаете, сейчас в тех областях деятельности, которые не связаны напрямую с наукой и техникой, стало ли людям нужнее знание математики, чем это было до активной цифровизации всего и вся?
— Мне кажется, что, наоборот, необходимости знать математику стало только меньше — именно потому, что всё, что можно автоматизировать, автоматизируется. Не автоматизируется живое общение. Непосредственно считать в уме чаще всего уже не нужно — нужно или быть разработчиком автоматизированных систем, или быть в круге профессий, которые в большей степени связаны с человеческой коммуникацией.
— Получается, многие математические знания скоро будут совсем не нужны?
— Есть такой исторический факт: изначально словом «компьютер» называли людей, которые профессионально выполняли вычисления. В США эту работу делали чернокожие женщины — это хорошо показано в фильме «Скрытые фигуры». Потом это всё исчезло и ушло, никто уже не пользуется логарифмической линейкой. И вопрос, сколько таких же ненужных кусочков математического знания сидит в современной программе, очень интересный.
Есть целая наука, curriculum studies, которая пытается понять, какие новые блоки должны быть в школьной программе, а какие уже не нужны, — через анализ исторического развития общества, а также интервью с разными профессионалами. В частности, то, что в российской школьной программе вычислению столбиком уделяются многие месяцы детской жизни, кажется довольно бессмысленным делом.
Зачем вообще нужно учиться математике
— Математическое и логическое мышление — разные вещи, но способствуют ли занятия математикой развитию логики?
— Действительно, решение математических задач — это упражнение на рассуждение и на просчёт многоходовых действий. И, наверное, в других учебных областях такой тренировки меньше. Поэтому оказывается, что дети, которые хорошо справляются с математикой, часто хороши в шахматах или в программировании — то есть там, где просчитывание нескольких ходов и их анализ — доминирующий навык.
— А какие ещё навыки лучше развиваются у тех, кто много занимается математикой? Например, пространственное мышление?
— Тут на самом деле сложная история. Некоторые люди — это относится и к детям, и к взрослым профессиональным математикам — решают математические задачи с опорой на визуальную модель. То есть им в принципе свойственно визуализировать. Но много и тех, кто оперирует определениями, алгебраическими формулами, а на визуальные конструкции почти не опирается. Соответственно, нагрузка на пространственное мышление и его тренировка в этих двух случаях будет разной.

В групповых исследованиях может найтись корреляция между математическим мышлением и пространственными способностями. Но это не означает, что одно способствует другому, что на индивидуальном уровне можно через развитие пространственных способностей улучшить математическое мышление или наоборот. Это значит просто, что некоторые из тех детей, кто хорошо решает задачи, хорошо справляются и с задачками на пространственную ориентацию.
— То есть пока нет никаких доказательств, что существует какая-то универсальная связь между занятиями математикой и пространственным мышлением?
— Да, таких доказательств нет. Причём и на индивидуальном уровне всё очень сложно. Визуальные модели обычно помогают на ранних этапах изучения какой-либо темы и чаще тем, кто плохо справляется с математическими предметами. Человек, который уже освоил предмет, справится с новой темой и без опор на визуальную модель. А если есть трудности, она может быть очень полезна. Но не всегда!
Чтобы визуальная модель помогла, нужно увидеть внутри неё абстрактное содержание. То есть для того чтобы «видеть математику» в визуальном материале, нужно ещё постараться. И иногда для ребят, которые справляются с математикой не очень хорошо, это тоже бывает отдельной большой когнитивной нагрузкой.
Есть такой любопытный феномен, что маленькие дети, когда их просят нарисовать какую-нибудь модель — например, показать на ней, что Вася выше Саши, а Саша выше Маши, — начинают рисовать персонажей с кудряшками, с одёжкой. Выхватить математическое соотношение и показать только его они не могут.
То есть восприятию абстрактного содержания в визуальных моделях надо научиться.
— Помогает ли изучение математики в дальнейшем быстро анализировать информацию и принимать решения во всех сферах жизни?
— Мне кажется, есть совершенно разные способы рассуждать. И они все по-своему ценны. Мне не хотелось бы усиливать давление, что якобы так важно знать именно математику.
Мне бы хотелось способствовать развитию такого сообщества, где навыки эмпатии, понимания исторического контекста, психосоматической саморегуляции и тому подобные ценятся ничуть не меньше, чем анализ информации. Ведь с анализом искусственный интеллект, как мы видим, всё равно справляется (или справится в ближайшем будущем) гораздо лучше нас. Хочется развивать такое образование, в котором другие важные навыки ценятся не меньше, чем математическое мышление.
Больше интересного про образование ― в нашем телеграм-канале. Подписывайтесь!











