Возрастание и убывание функции: как понять и простить найти
Определяем интервалы, экстремумы и разбираемся в графиках.

Функции — это математический инструмент для описания изменяющихся величин в реальном мире. Температура воздуха, курс валют, скорость интернета — всё это можно выразить с помощью функции. Она может плавно расти, резко падать или несколько раз менять направление.
Чтобы работать с такими процессами, нужно научиться анализировать поведение функции: понимать, где она растёт, где убывает и в каких точках достигает крайних значений. Давайте выясним, как это сделать.
Содержание
- Что такое функция
- Возрастание и убывание функции
- Условия возрастания и убывания функции
- Экстремумы функции: максимумы и минимумы
- Определение промежутков монотонности функции
Что такое функция и как её представить
Функция — это правило, которое устанавливает зависимость одной величины от другой. Например, чем сильнее огонь под кастрюлей, тем быстрее закипит вода. В этом случае температура нагрева (независимая переменная) определяет время закипания воды (зависимая переменная).
В математике независимую величину обычно обозначают буквой x, а зависимую — буквой y. Запишем эту зависимость с помощью формулы:
В этой формуле:
- f — название функции;
- x — значение, которое мы подаём на вход функции;
- y — результат, который функция возвращает после вычисления.
Рассмотрим простой пример линейной функции на основе расчёта зарплаты. Предположим, менеджер по продажам получает базовую ставку 30 000 рублей. Кроме того, за каждую сделку он получает ещё по 5000 рублей. Такую систему можно описать как функцию: зарплата зависит от количества сделок — чем больше сделок, тем выше зарплата. Здесь зарплата — это зависимая переменная, а количество сделок — независимая: S(x) = 30 000 + 5000x. Разберём каждый элемент:
- S(x) — размер зарплаты, где S означает salary (зарплата), а x — количество сделок;
- 30 000 — базовая ставка в рублях, которую менеджер получает независимо от количества сделок;
- 5000x — бонусная часть, где 5000 — плата за одну сделку, а x — количество сделок.
Если менеджер заключил три сделки за месяц, то его зарплата составит:
S(3) = 30 000 + 5000 × 3 = 45 000 рублей.
Функцию можно представить не только с помощью формул, но и с помощью таблиц, графиков, текстового описания, диаграмм и программного кода. Выбор способа представления зависит от конкретной задачи: формулы удобны для вычислений, таблицы наглядно отображают конкретные значения, а графики позволяют увидеть общую картину зависимости.
Представим нашу функцию зарплаты менеджера в табличном виде:
| Количество сделок (x) | Зарплата S(x) в рублях | Расчёт |
|---|---|---|
| 0 | 30 000 | 30 000 + 5000 × 0 |
| 1 | 35 000 | 30 000 + 5000 × 1 |
| 2 | 40 000 | 30 000 + 5000 × 2 |
| 3 | 45 000 | 30 000 + 5000 × 3 |
| 4 | 50 000 | 30 000 + 5000 × 4 |
Как видно из таблицы, при увеличении количества сделок на один зарплата увеличивается на 5000 рублей: это наглядно демонстрирует линейную зависимость между количеством сделок и размером зарплаты.
Ниже представлен график этой же функции. На нём мы можем наглядно увидеть зависимость зарплаты от количества сделок: по горизонтальной оси x отмечено количество сделок (независимая переменная), а по вертикальной оси y — размер зарплаты в рублях (зависимая переменная).
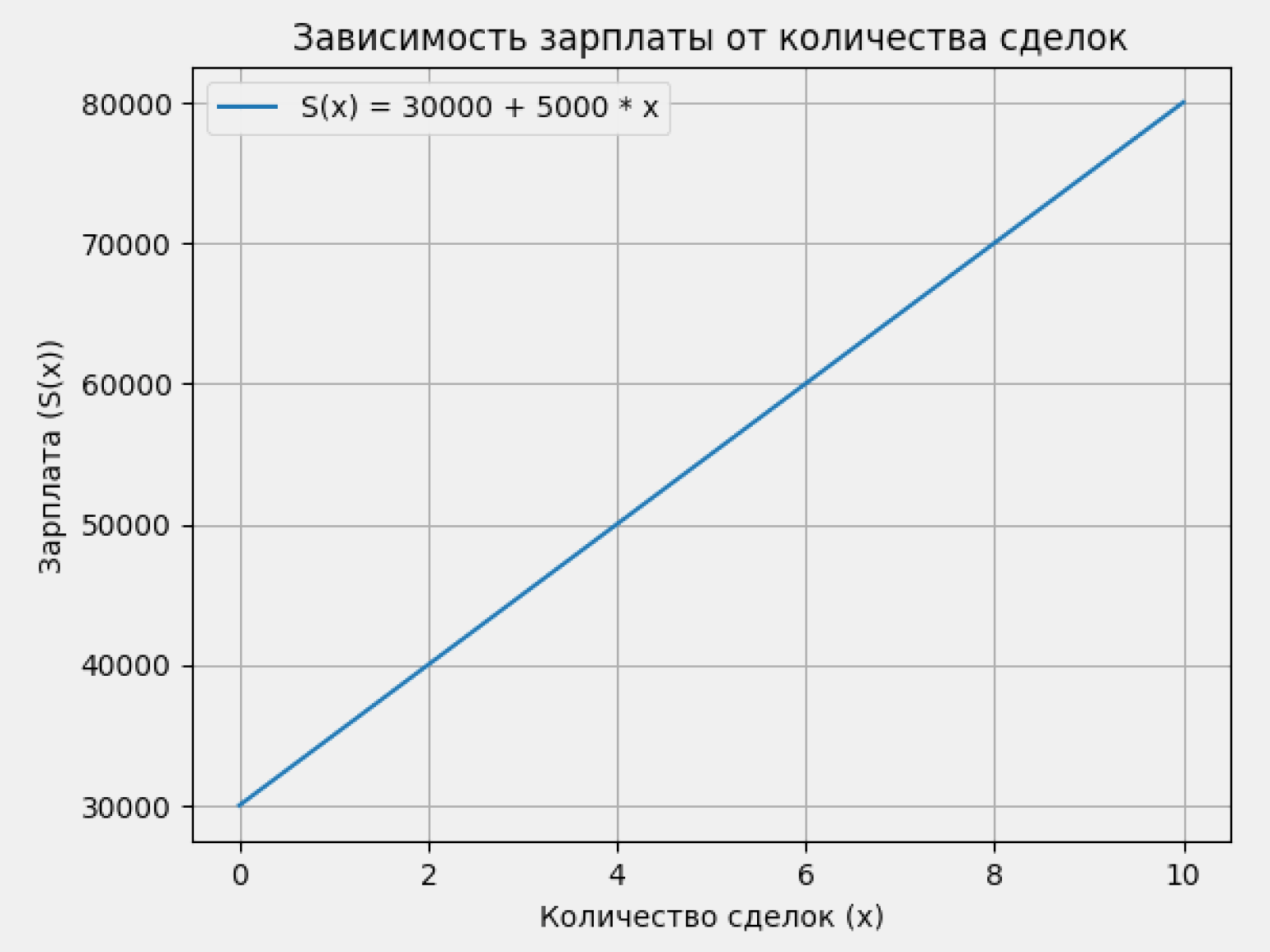
Изображение: Google Colab / Skillbox Media
Для практики сделайте копию файла functions.ipynb и откройте его в Google Colab — в нём собраны примеры функций из этой статьи. Вы можете менять различные параметры и сразу видеть, как это влияет на график.
Например, попробуйте в линейной функции зарплаты изменить базовую ставку с 30 000 на 40 000 рублей или увеличить бонус за сделку с 5000 до 7000 рублей — и посмотрите, как изменится прямая на графике.
Характер изменения функции: возрастание и убывание
Функция может вести себя по-разному: на одних участках она возрастает, на других — убывает, а где-то остаётся неизменной. Это можно сравнить с изменением температуры в летний день: утром она плавно повышается, днём сохраняется примерно на одном уровне, а к вечеру понижается.
Чтобы определить характер поведения функции, нам нужно взять любые две точки на графике — назовём их x₁ и x₂. При этом точка x₁ должна быть левее x₂ (x₁ < x₂). Когда мы сравним значения функции f(x) в этих точках, то сможем понять, как ведёт себя функция. Возможные варианты:
- Если значения увеличиваются, то функция возрастает: f(x₁) < f (x₂) при x₁ < x₂. Например, если f(1) = 2, а f(2) = 5, то 2 < 5.
- Если значения уменьшаются — функция убывает: f(x₁) > f(x₂) при x₁ < x₂. Пример убывающей функции: если f(1) = 7, а f(2) = 4, то 7 > 4.
- Если значения неизменны — функция сохраняет постоянное значение: f(x₁) = f(x₂) при x₁ < x₂. Пример: f(1) = 3, f(2) = 3.
Чтобы наглядно увидеть, как функция изменяет своё поведение на разных участках, рассмотрим f(x) = x². На интервале от минус бесконечности до нуля (−∞, 0) функция убывает, в точке x = 0 достигает минимума, а на интервале от нуля до плюс бесконечности (0, +∞) возрастает. В результате на графике получается знакомая со школы кривая — парабола.
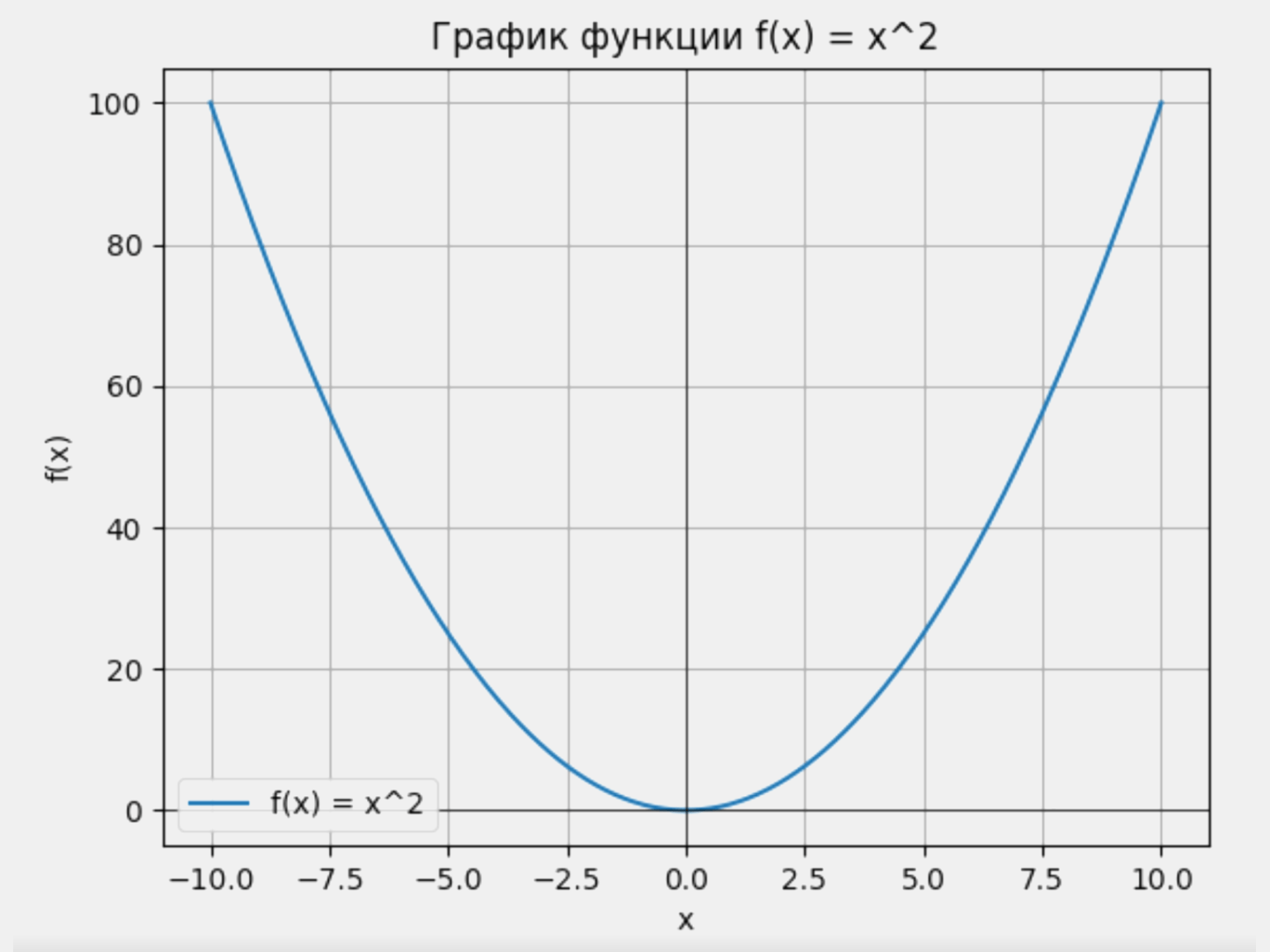
Изображение: Google Colab / Skillbox Media
В этом разделе мы рассмотрели, как визуально определять участки возрастания и убывания функции по её графику. Далее мы познакомимся с более точным методом анализа — с помощью производной функции.
Условия возрастания и убывания функции
Производная функции — это скорость её изменения в каждой точке. Подобно спидометру в движущемся автомобиле, она показывает, как быстро и в каком направлении (вверх или вниз) меняется значение функции в конкретный момент. Поэтому по знаку производной можно определить, как ведёт себя функция: возрастает, убывает или остаётся постоянной. Это называется достаточным условием монотонности.
Производная положительна: f'(x) > 0. В этом случае функция строго возрастает на всём промежутке — каждое следующее значение больше предыдущего. Возьмём, например, линейную функцию f(x) = 2x + 1. Её производная равна f'(x) = 2, то есть функция растёт с постоянной скоростью. Поэтому она возрастает при любых значениях x:
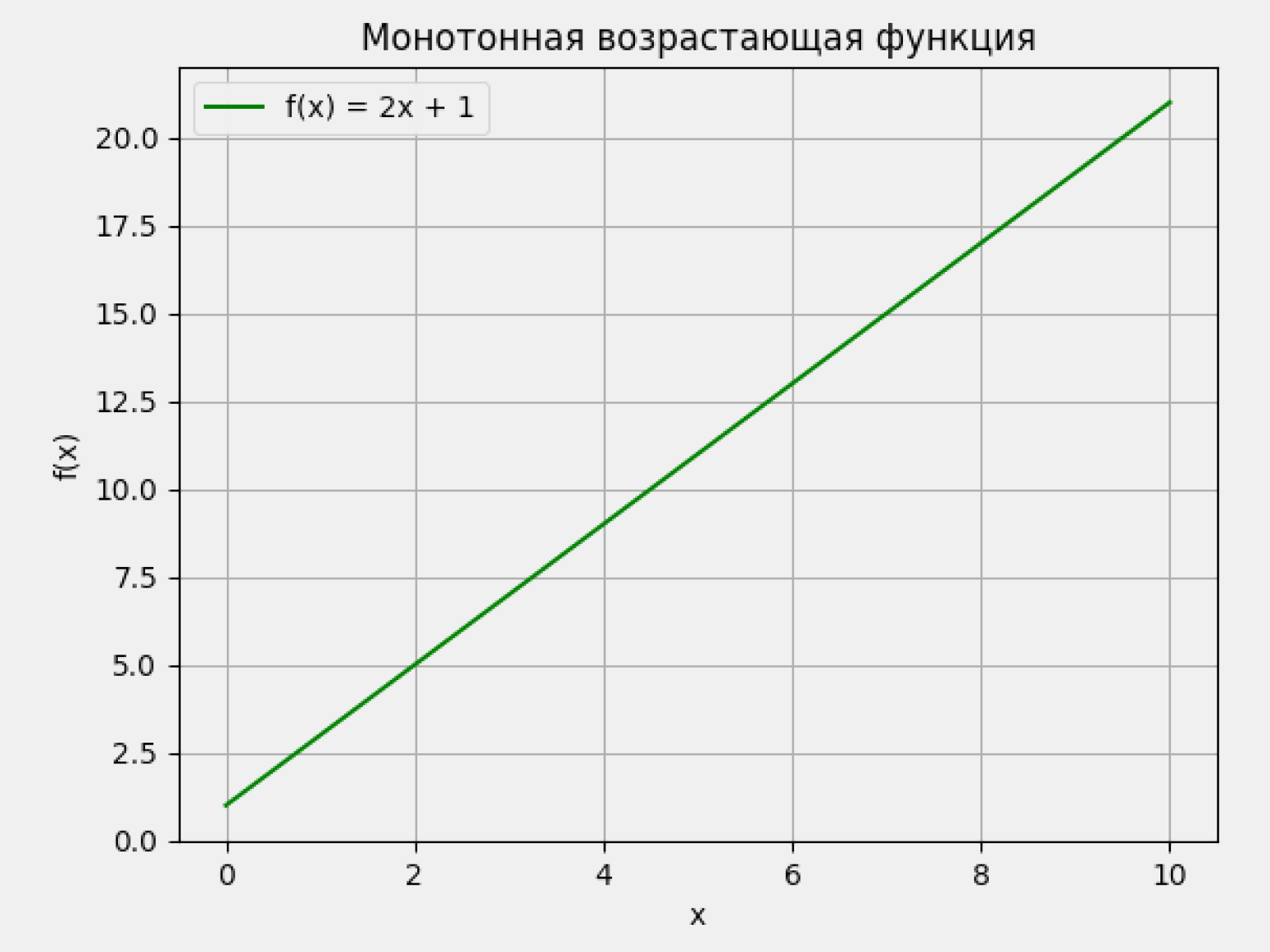
Производная отрицательна: f'(x) < 0. Когда производная меньше нуля, функция убывает — то есть её значения последовательно уменьшаются. Например, возьмём функцию f(x) = −3x + 10. Её производная f'(x) = −3 остаётся отрицательной при любом x:
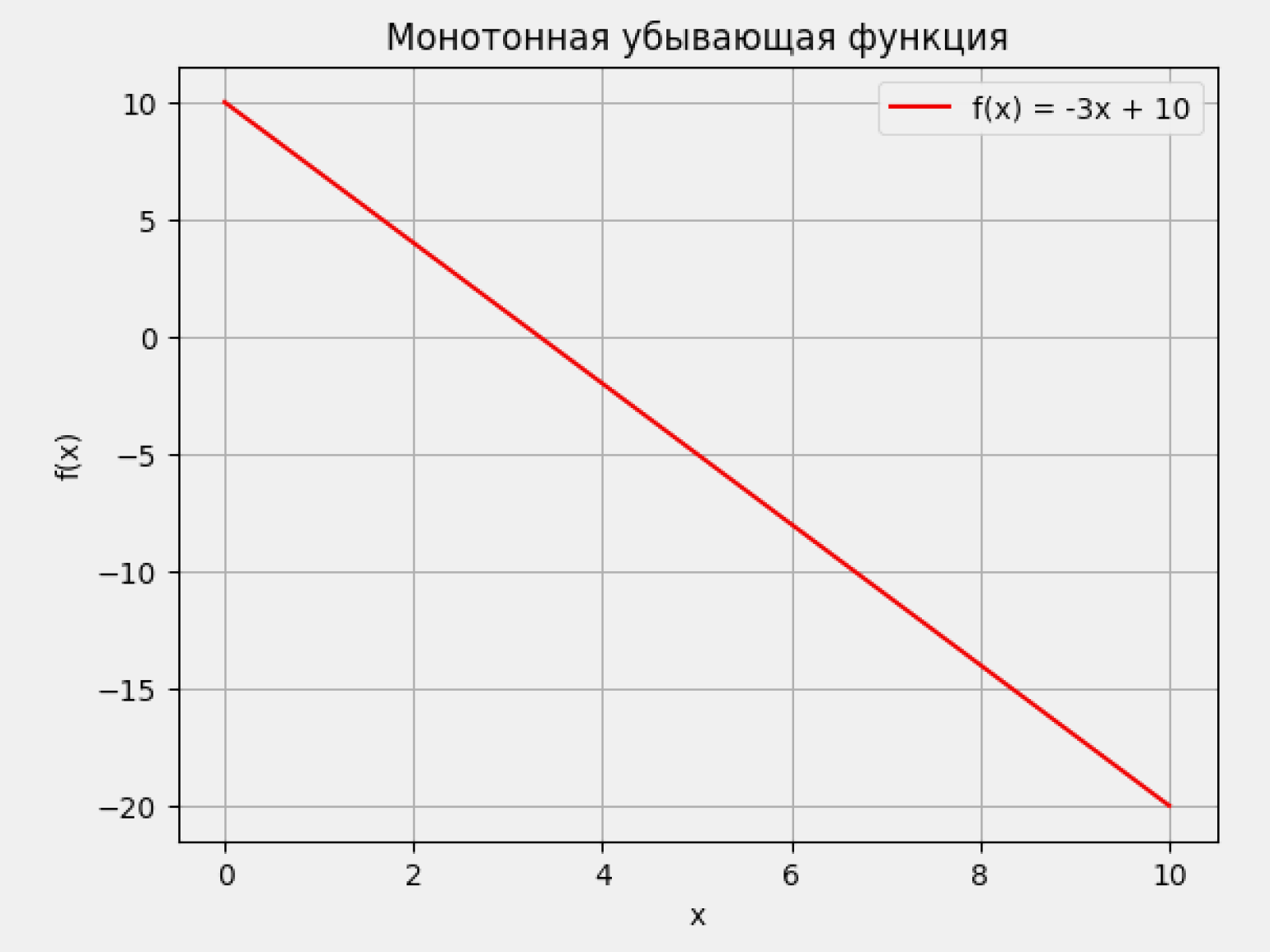
Производная равна нулю: f'(x) = 0. Если производная равна нулю на всём промежутке, функция остаётся постоянной и не меняет значения. Это хорошо видно на функции f(x) = 5. Её производная f'(x) = 0 при любом x, поэтому график выглядит как горизонтальная прямая:
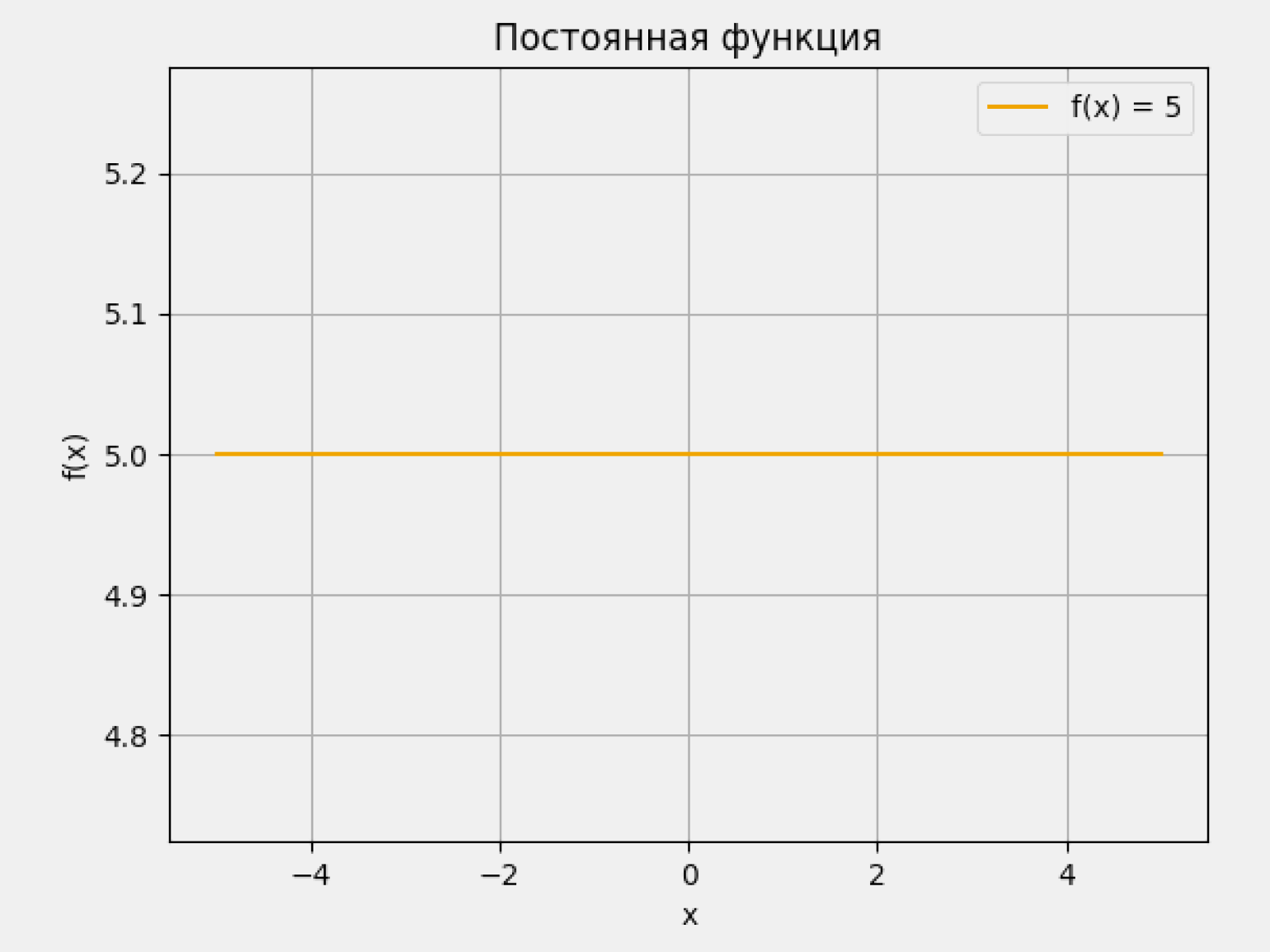
Важно отметить, что не все функции ведут себя одинаково (монотонно) на всей области определения. Некоторые из них могут менять характер поведения: возрастать на одних интервалах, а убывать на других. Это похоже на движение по холмистой местности — с чередующимися подъёмами и спусками. Такие функции называются немонотонными.
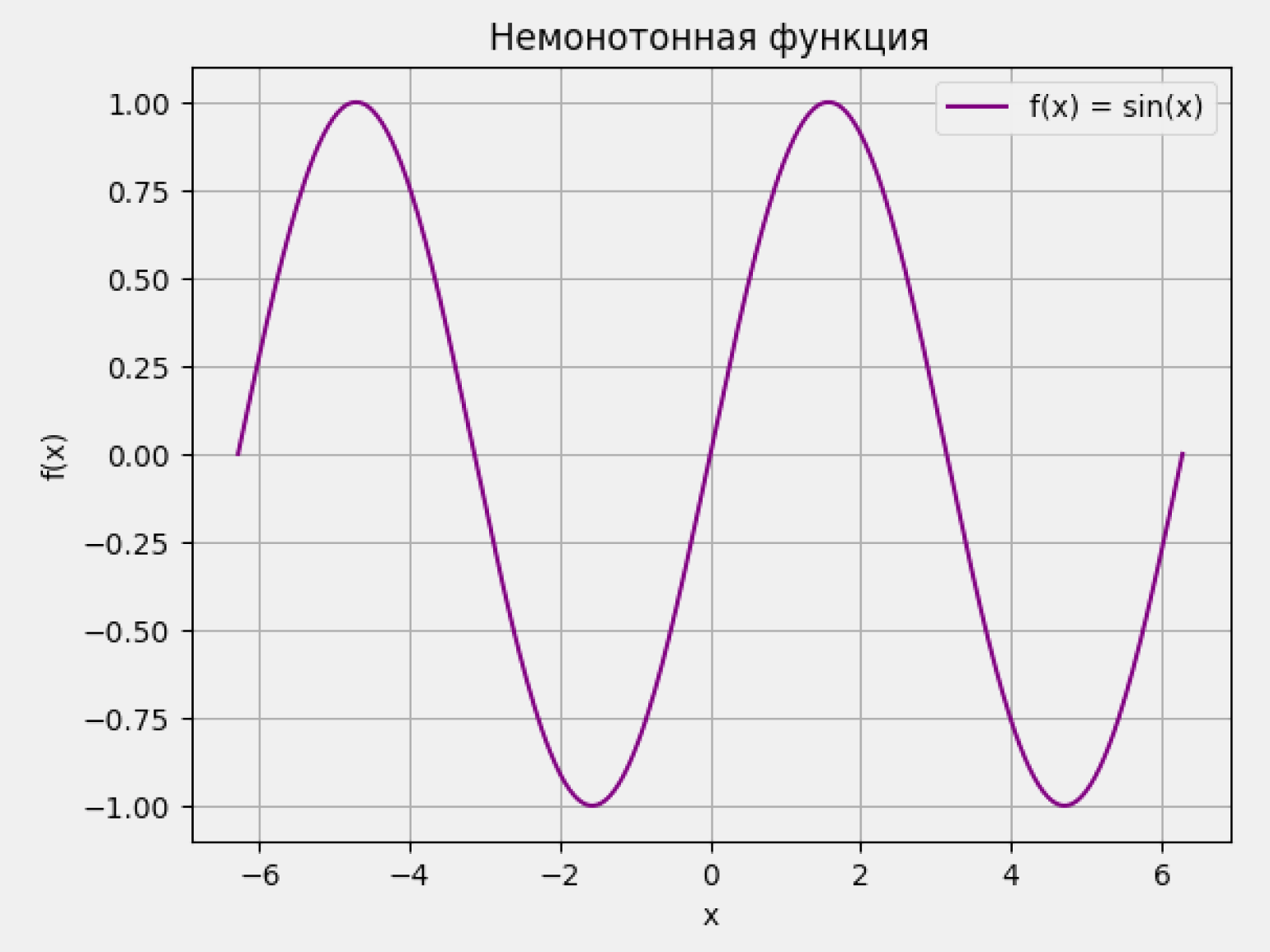
Рассмотрим поведение немонотонной функции f(x) = sin(x):
- она возрастает на (−π, 0), (0, π), (2π, 3π) и так далее — во всех промежутках, где её производная f'(x) = cos(x) положительна;
- убывает на (0, π), (π, 2π) и других интервалах, где cos(x) принимает отрицательные значения;
- достигает максимумов и минимумов в точках, где f'(x) = 0.
Производная функции f(x) = sin(x) периодически меняет знак — с положительного на отрицательный и обратно. В результате образуется волнообразный график, где функция поочерёдно возрастает и убывает:
Как найти точки экстремума функции
Точка экстремума — это точка на графике функции, в которой меняется направление её движения: с возрастания на убывание или наоборот. В такой точке производная либо равна нулю (если существует), либо не существует вовсе — например, при разрыве или изломе графика.
Есть два типа точек экстремума: точки максимума и минимума. Чтобы их определить, нужно выполнить следующие действия:
- сначала найти производную функции;
- определить, где производная равна нулю или не существует;
- после проверить, меняется ли знак производной в этих точках, — именно смена знака укажет на наличие максимума или минимума.
Давайте потренируемся на примере функции f(x) = x³ − 3x² + 2.
Вычисляем производную. Поскольку производная суммы равна сумме производных, поэтому мы будем считать по частям:
- производная от x³ — это 3x²;
- производная от −3x² — это −6x;
- производная от константы 2 — это 0.
Складываем полученные выражения: f'(x) = 3x² − 6x.
Вынесем общий множитель за скобки, чтобы дальше нам было проще находить нули производной: f'(x) = 3x (x − 2).
Находим критические точки. Производная обращается в ноль, когда выражение 3x(x − 2) равно нулю. То есть нам нужно найти такие значения x, при которых это произведение станет равным нулю: 3x(x − 2) = 0.
В этом выражении есть три множителя: 3, x и (x − 2). Числовой коэффициент 3 можно не учитывать, поскольку он не влияет на результат: произведение равно нулю только в том случае, если хотя бы один из множителей (x или x − 2) равен нулю. Давайте это проверим:
- x = 0 → первый множитель равен нулю;
- x − 2 = 0 → отсюда находим x = 2.
Получается, производная равна нулю в двух точках: x = 0 и x = 2.
Проверяем изменение знака производной. Теперь определим, как меняется знак производной при переходе через каждую критическую точку, — это поможет установить характер экстремума (максимум или минимум). Для проверки выберем значения x немного меньше и немного больше каждой точки и подставим их в выражение производной:
- если производная меняется с плюса на минус — это означает, что функция сначала возрастала, а затем начала убывать → максимум;
- если производная меняется с минуса на плюс — функция сначала убывала, а потом начала возрастать → минимум.
Давайте возьмём значения x, которые чуть меньше и чуть больше найденных точек, и подставим их в производную f'(x) = 3x(x − 2).
Начнём с точки x = 0 и выберем для неё значения −1 и 1:
- подставим x = −1 → f'(−1) = 3 × (−1) × (−1 − 2) = 9;
- подставим x = 1 → f'(1) = 3 × 1 × (1 − 2) = −3.
Производная меняет знак с положительного (9) на отрицательный (−3). Это значит, что в точке x = 0 функция достигает локального максимума.
Перейдём к точке x = 2 и возьмём значения 1 и 3:
- подставим x = 1 → f'(1) = 3 × 1(1 − 2) = −3;
- подставим x = 3 → f'(3) = 3 × 3(3 − 2) = 9.
Производная меняет знак с отрицательного (−3)на положительный (9). То есть в точке x = 2 функция достигает своего минимума.
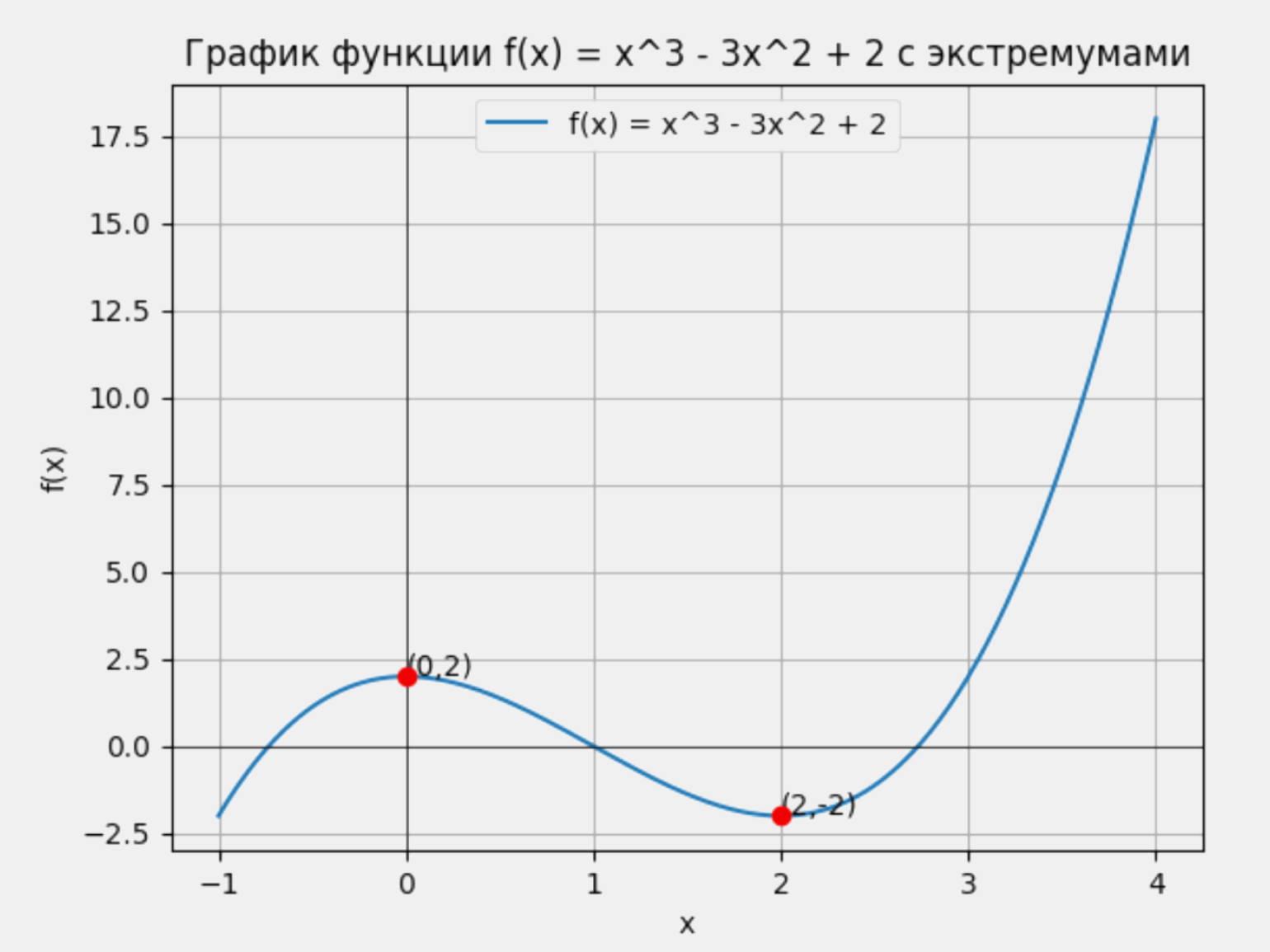
Изображение: Google Colab / Skillbox Media
Интервалы возрастания и убывания функции
В предыдущем разделе мы определили точки экстремума (максимума и минимума) и проанализировали поведение функции слева и справа от этих точек. Теперь объединим эти результаты и найдём промежутки монотонности — интервалы, на которых функция возрастает или убывает.
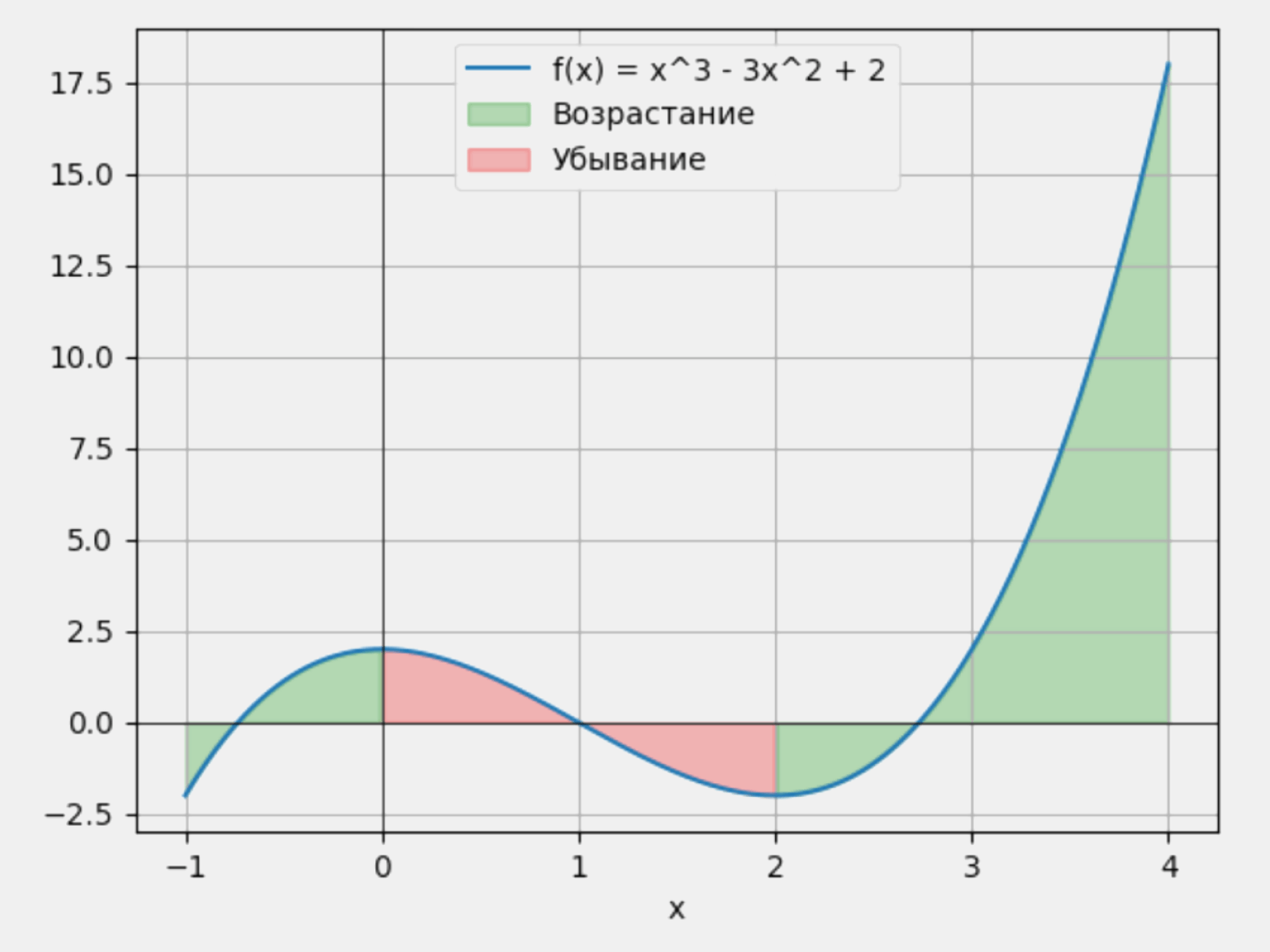
Рассмотрим уже знакомую нам функцию f(x) = x³ − 3x² + 2:
- производная: f'(x) = 3x(x − 2);
- критические точки: x = 0 и x = 2;
- изменение функции на интервалах:
- (−∞, 0) — функция возрастает, поскольку производная положительна;
- (0, 2) — функция убывает, производная отрицательна;
- (2, +∞) — функция снова возрастает.
Наш анализ показывает, что функция возрастает на двух интервалах: (−∞, 0)
и (2, +∞), в то время как на интервале (0, 2) функция убывает. Это подтверждается знаком производной на каждом из этих промежутков:
📌 Для закрепления материала попробуйте самостоятельно найти интервалы возрастания и убывания функции f(x) = x⁴ − 4x². Начните с нахождения производной, затем определите критические точки и проанализируйте знак производной на каждом интервале.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!