Три программиста и отпуск

Запутанная задача на логику. Распутываем вместе с репетитором.

Альберто Блинчиков для Skillbox Media

Александр Бабаскин

Автор статей о программировании. Изучает Python, разбирает сложные термины и объясняет их на пальцах новичкам. Если что-то непонятно — возможно, вы ещё не прочли его следующую публикацию.

Анна Никитина

Преподаватель математики, автор YouTube-канала «Математика с Аней» и соавтор учебников и методических рекомендаций к учебникам по математике.

Анна готовит учеников к ЕГЭ в школе «Топскул» и консультирует онлайн-школы по вопросам эффективного обучения.

Условие

Три друга-программиста решили отправиться в отпуск и теперь выбирают, куда им ехать. У них есть четыре варианта: Рим, Брюссель, Осло и Норильск. Однако они не смогли договориться и решили провести голосование. Правила такие:

Сначала голосуют за поездку в Рим. Если хотя бы двое будут ЗА — голосование прекращается и все отправляются в Рим.
Если большинство не поддержит идею с Римом — голосуют по поездке в Брюссель.
Если и с Брюсселем не сложится — голосуют по поводу Осло.
Если и с Осло не получится — все отправятся загорать в Норильск.

Каждый программист действует безупречно логично: знает свои приоритеты и приоритеты других участников. Например, первый программист больше всего хочет попасть в Осло. Но если коллеги его не поддержат, он выберет Норильск. Если и с Норильском не сложится, остаётся Рим. Ну и на крайний случай — Брюссель. Приоритеты всех участников — в таблице:

Вопрос: какой город выберут программисты и будет ли это лучшим решением для большинства?

Подсказка

В условии задачи есть фраза: «Каждый программист действует безупречно логично». А значит, все герои голосуют по безупречно логичным правилам — последовательно, непротиворечиво, не подчиняясь принципам человеческой психологии и общепринятым правилам поведения:

Безупречно логичное поведение	Суровая жизненная реальность
Если в задаче сказано, что программист 20 лет не опаздывает, не ходит в отпуск и не требует повышения, то так и есть.	В жизни почти все программисты хоть иногда опаздывают, регулярно ходят в отпуск и стремятся к карьерному росту.
Если нужно проголосовать по строгим правилам, то каждый участник будет следовать этим правилам от начала и до конца.	Кто-то из участников может смухлевать, кто-то поймёт правила по-своему и нарушит их, а кто-то вообще может проигнорировать правила и само голосование.
Безупречно логичные персонажи думают о личной выгоде, никому не помогают и ни с кем не договариваются.	Несколько программистов с общим интересом могут договориться и увеличить свои шансы на получение желаемого результата.
Все действуют в личных интересах и всегда знают приоритеты других персонажей. Следовательно, все принимают решения, отталкиваясь от предположительных действий других участников.	Всегда сложно узнать, как и о чём думают другие люди.

В задачах на безупречную логику нужно распутывать решение с конца. У нас есть конечное количество участников и действий, которые нужно обязательно выполнить, — то есть процессы не бесконечны и их можно выстроить последовательно, один за другим.

Ещё обратите внимание на формулировку вопроса. Она предполагает два ответа: 1) куда поедут программисты и 2) будет ли это лучшим решением для большинства. Первый вопрос проверяет навык логического мышления; второй — внимательность.

Решение

Куда поедут программисты

Шаг №1. Программисты будут делать выбор между четырьмя городами, но проводят три этапа голосования — поедут они в Норильск или нет, зависит от голосования за Осло. То есть на третьем этапе они будут выбирать между Осло и Норильском — потому что варианта поехать в Рим или Брюссель к тому времени не останется.

Смотрим таблицу приоритетов участников и понимаем, что на третьем этапе первый и второй программисты проголосуют ЗА Осло, а третий — ПРОТИВ. Вывод: если голосование дойдёт до третьего этапа, то программисты отправятся в Осло, а не в Норильск. Уже неплохо :)

Шаг №2. Теперь предположим, что голосование не дойдёт до третьего этапа. В этом случае программисты будут выбирать между поездкой в Брюссель и Осло, так как мы уже увидели — на третьем этапе они точно не выберут Норильск. А значит, первый программист проголосует ПРОТИВ поездки в Брюссель, а второй и третий — ЗА. Победит Брюссель.

Шаг №3. Поднимемся на следующую ступеньку и узнаем, что будет с голосованием за Рим. Здесь участники делают выбор между Римом и Брюсселем. Почему так? Да потому, что они уже понимают: на втором этапе голосования точно победит Брюссель.

Первый и третий программист проголосуют ЗА поездку в Рим, а второй — ПРОТИВ. То есть вариант с отпуском в Риме будет принят после первого голосования. Отлично!

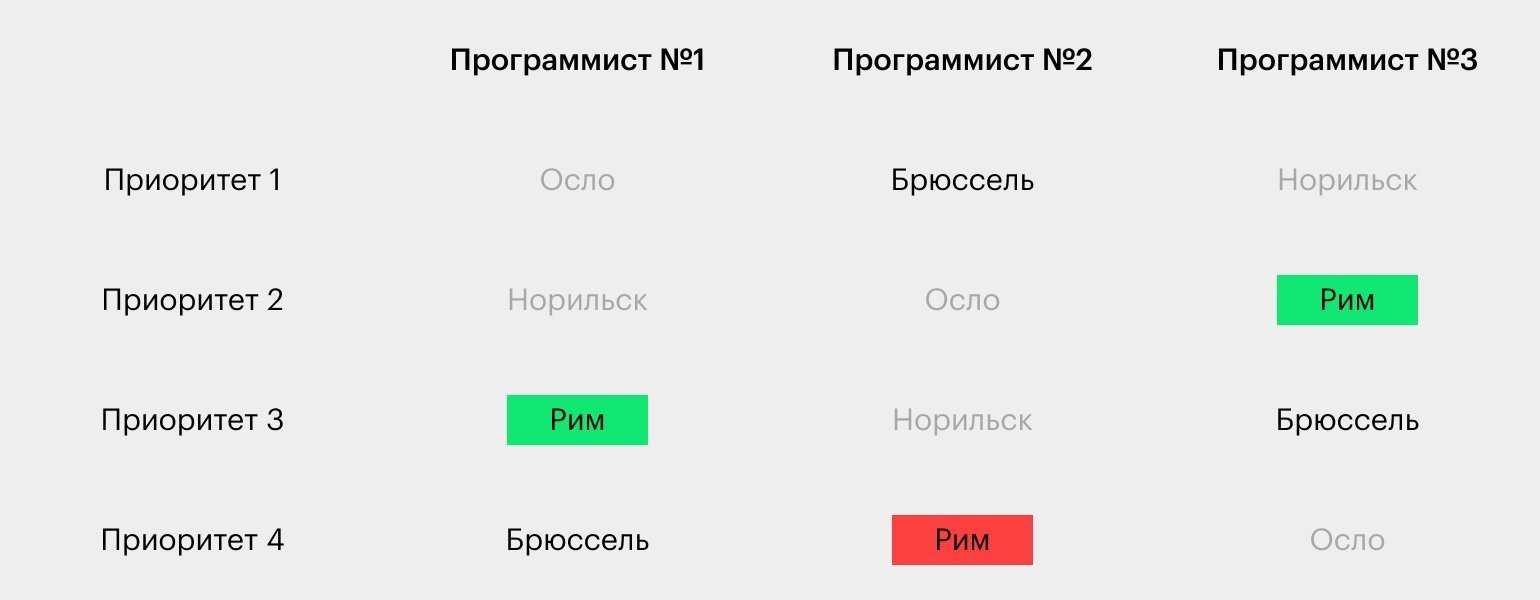
Итог: программисты поедут в Рим.

Какое решение будет лучшим для большинства

Теперь разберёмся со второй частью вопроса. Если голосование пройдёт без учёта безупречно логичных правил, то на исход повлияет договорённость между участниками. Рассмотрим два возможных сценария.

Первый сценарий. Первый и второй программист объединятся и выберут Осло — в их общей системе приоритетов этот город стоит выше, чем Рим.

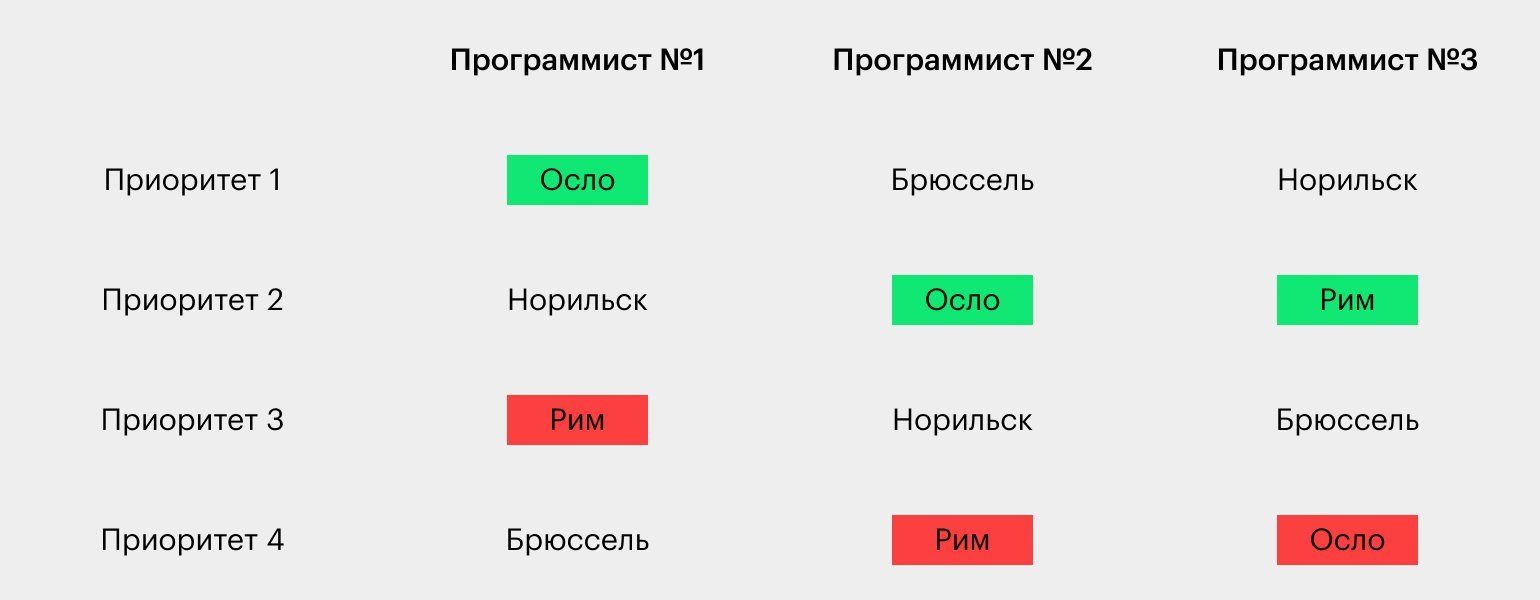
По-другому двум программистам объединяться невыгодно:

Если первый участник объединится с третьим, то они выберут Норильск. Это невыгодно первому участнику, который предпочитает Осло, и, чтобы организовать поездку в город своей мечты, он может договориться со вторым программистом.
Если второй участник объединится с третьим, то они будут выбирать между Брюсселем и Норильском. У первого программиста Норильск в приоритетах стоит выше Брюсселя, поэтому на общем голосовании победит Норильск. Второму программисту это невыгодно, поскольку он предпочитает Брюссель или Осло — то есть может договориться с первым участником о поездке в Брюссель или Осло.

Итог: если два программиста смогут договориться, то лучшим решением для большинства будет поездка в Осло.

Второй сценарий. Первый и второй участник не могут объединиться и должны искать компромисс с третьим программистом. В этом случае оптимальным решением будет Норильск, поскольку по сумме всех приоритетов он окажется выше Осло, Брюсселя и Рима.

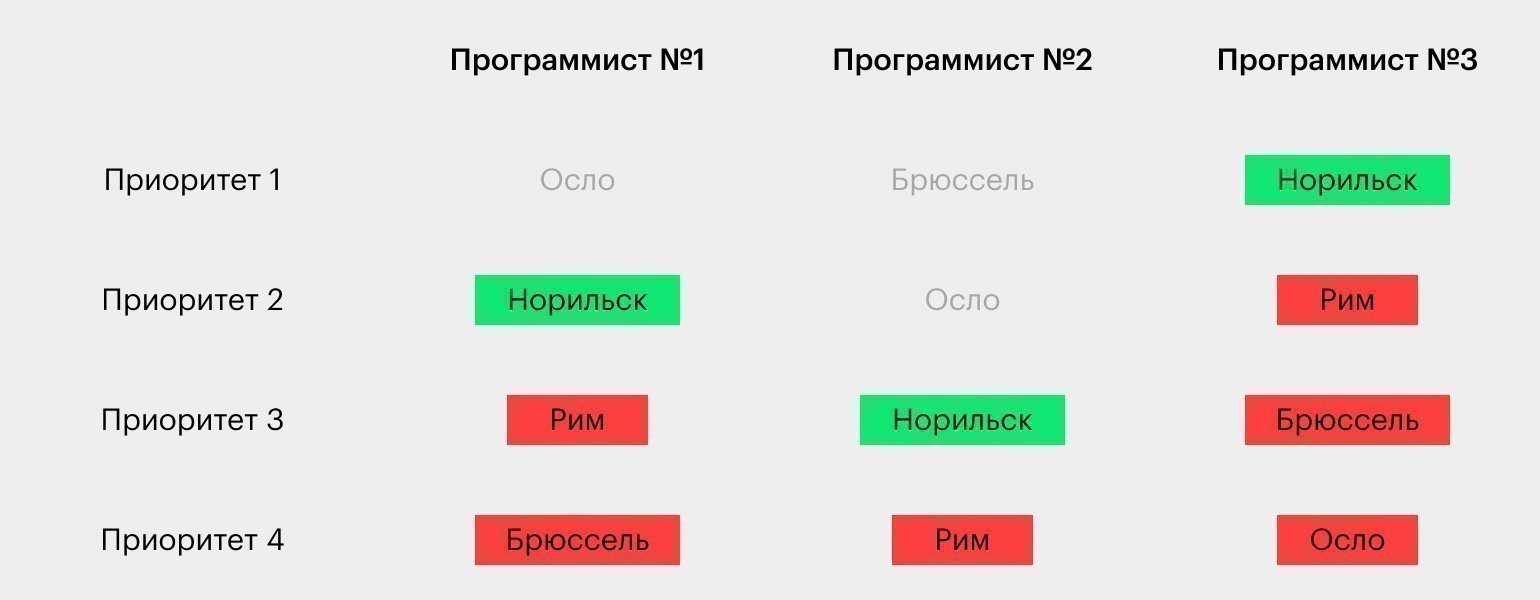
Добавим к графику расчёты:

У первого программиста Норильск стоит на втором месте; у второго — на третьем; у третьего — на первом. В сумме Норильск наберёт 6 баллов.
Осло — 7 баллов.
Брюссель — 8 баллов.
Рим — 9 баллов.

Итог: чем меньше баллов, тем выше приоритет. Следовательно, если программисты попытаются договориться и математически учесть все приоритеты, лучшим решением для большинства будет Норильск.