Теория вероятностей: как научиться предсказывать случайные события
Разбираем основные понятия, решаем задачи и делаем первый шаг на пути к карьере в data science.


Продолжаем разбираться с математическими концепциями, на которых держится современное IT. Сегодня поговорим о теории вероятностей — разделе математики, который широко используется в машинном обучении, геймдеве, статистике и науке о данных.
Из этой статьи вы узнаете:
Что такое теория вероятностей
Теория вероятностей — это наука, которая изучает мир случайностей и пытается их предсказать. Здесь встречаются такие понятия, как «события» и «вероятности», у которых, в свою очередь, есть свои свойства и операции — о них мы поговорим чуть позже.
Проще всего продемонстрировать, как работает теория вероятностей, на примере подбрасывания монетки. В этом случае у нас есть два варианта: орёл или решка, а значит, шанс выпадения каждой из сторон одинаковый и составляет 50%.
Изображение: Google
Но как убедиться, что это действительно так? Например, я могу подбросить монетку десять раз, и мне магическим образом девять раз подряд выпадет орёл и один раз решка. Значит ли это, что шанс выпадения орла — 90%? Конечно, нет — и у этого есть научное объяснение.
Дело в том, что теория вероятностей рассматривает случайные события в рамках бесконечности. Иными словами, если мы будем подбрасывать монетку бесконечное количество раз, то шансы выпадения орла или решки будут приближаться к 50%.
В математике такая закономерность называется законом больших чисел, и этот закон — один из фундаментальных для data science. Фишка в том, что чем больше данных мы имеем на руках, тем точнее можно делать предсказания. Подробнее об этом читайте в статье «Математика для джунов».
Такая же логика работает и для других случайных явлений — например, шанс выпадания числа 5 на игральном кубике равен 1 к 6, а вероятность того, что молния ударит в одно и то же место дважды — примерно 1 к 500.
Изображение: Google
Теория вероятностей помогает нам предсказывать шанс возникновения различных событий, когда ответ не такой однозначный и на события влияет множество факторов.
Основные понятия
Мы упомянули слова «событие» и «вероятность», но не рассказали, что они вообще значат в контексте теории вероятностей. Давайте разбираться.
События
Событие — это всё, что может произойти, когда мы совершаем какое-то действие. Например, если мы бросаем монетку, то событие — это выпадение орла или решки. Чтобы обозначать события, используют заглавные буквы латинского алфавита. Например, для орла можем выбрать букву A, а для решки — B.
Существует много разных видов и классификаций событий, но в этой статье мы остановимся на основных четырёх:
- Достоверные — те, которые точно произойдут. Если бросить стакан на пол, то с вероятностью 100% он полетит вниз.
- Невозможные — те, которые никогда не произойдут. Если бросить тот же стакан на пол, то он никогда не полетит вверх (мораль: не стоит бросать стаканы на пол, если, конечно, вы не на МКС).
- Случайные — те, которые могут произойти, а могут и не произойти. Например, если мы бросаем игральный кубик, то не можем с уверенностью сказать, что выпадет число 2.
- Несовместимые — те, которые исключают друг-друга. Например, при подбрасывании монетки может выпасть либо орёл, либо решка — оба одновременно они выпасть не могут.
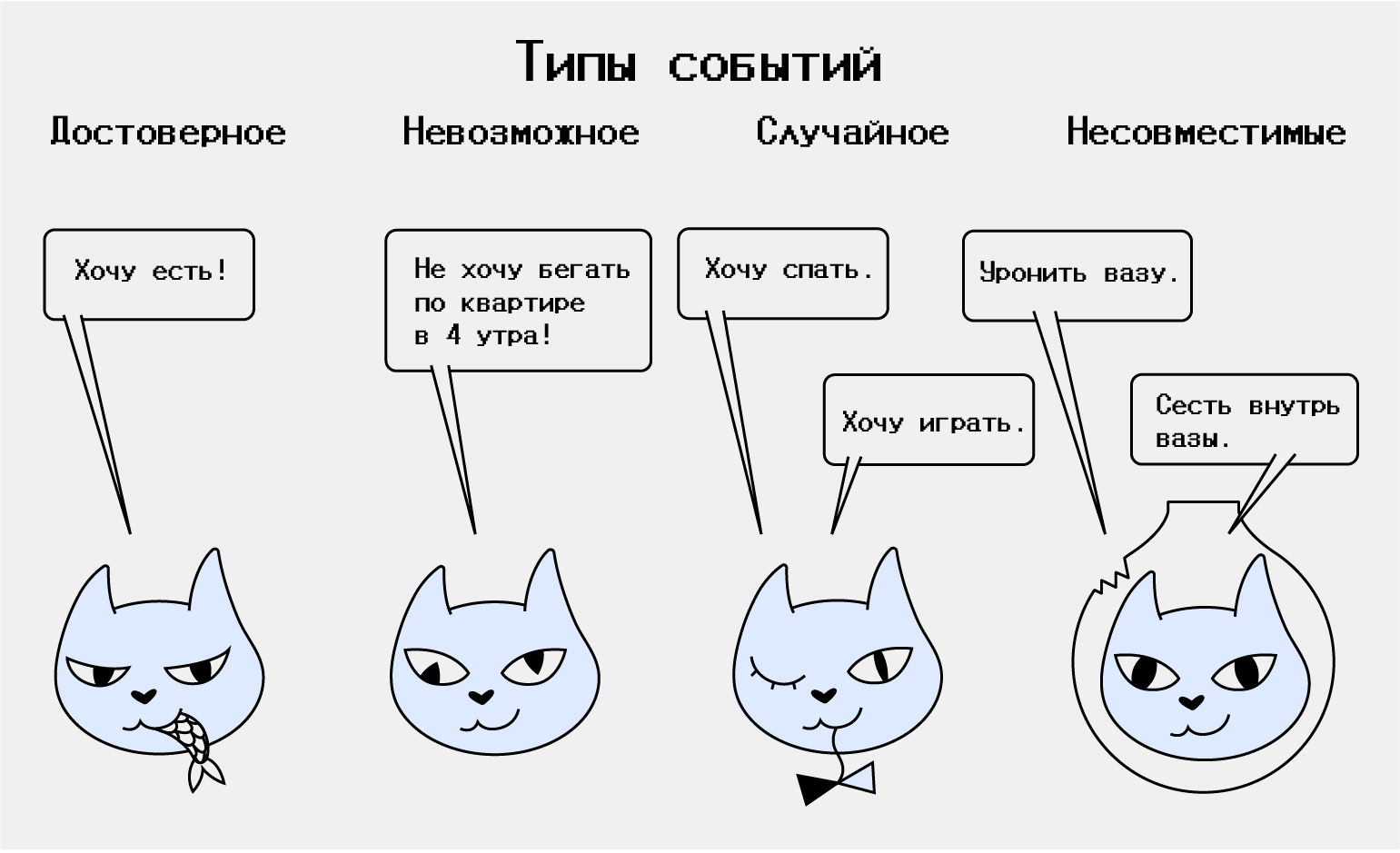
Инфографика: Оля Ежак для Skillbox Media
Если собрать все несовместимые события вместе, они будут называться полной группой событий. Это множество событий, одно из которых обязательно случится, если мы совершаем действие, а другие — не произойдут никогда. Например, когда мы бросаем игральный кубик, может выпасть только одна из сторон.
Вероятности
Вероятность — это число, которое обозначает шанс возникновения события. Например, вероятность выигрыша в лотерею может составлять 1 к 1 000 000.
Мы записывали значения вероятностей в процентах и отношениях, но математикам удобнее располагать их в диапазоне от 0 до 1. Если вероятность равна 0, то событие никогда не произойдёт, а если 1 — точно произойдёт. Всё, что посередине, — это случайные события.
Самый простой способ вычислить вероятность — поделить число благоприятных событий на общее число возможных событий. Например, если всего в колоде 36 карт, а мы хотим достать короля пик, то вероятность этого события равна 1/36, или 0,03. Если бы нас устроил любой из королей, то вероятность была бы равна 4/36 — то есть 0,1.
К формулам мы ещё вернёмся, а пока отметим, что вероятность — это не всегда точное предсказание, а лишь оценка шанса возникновения события. Как следует из закона больших чисел, если шанс выпадения орла и решки равен 50%, это не означает, что они будут выпадать по очереди.
Ещё вероятность может быть условной — или зависеть от другого события. Например, если мы хотим вытащить любой туз из колоды карт, шанс равен 4/36. Но если до этого кто-то уже вытащил одного туза, то вероятность будет равна 3/35. Это потому, что в колоде стало на одну карту меньше и количество благоприятных событий тоже уменьшилось.
С определениями закончили — теперь давайте узнаем, как событиями можно управлять.
Что такое алгебра событий
Когда мы считаем вероятности, нас может устраивать более чем один результат событий. Или другая ситуация — нам может быть важно, чтобы два события выполнялись вместе. В таких случаях на помощь приходит алгебра событий. Разбираемся, какие действия она позволяет совершать.
Дисклеймер: в этом разделе мы не рассматриваем вычитание и дополнение событий, потому что они довольно сложны для первого знакомства с теорией вероятностей. Возможно, скоро мы выпустим о них отдельную статью.
Сложение (объединение) событий
Сумма двух событий A + B — это сложное событие, которое произойдёт, если случится или событие A, или событие B, или оба одновременно.
Допустим, мы хотим вычислить вероятность выпадения на кубике стороны с числами 2 или 4. Обозначим событие «выпадение стороны 2» как A, а событие «выпадение стороны 4» как B. Так как у кубика всего шесть граней, вероятность выпадения каждой из этих сторон равна 1/6.
А так как нас интересует либо событие A, либо событие B, мы ищем сумму этих событий — A + B. Вычисляем соответствующие вероятности:
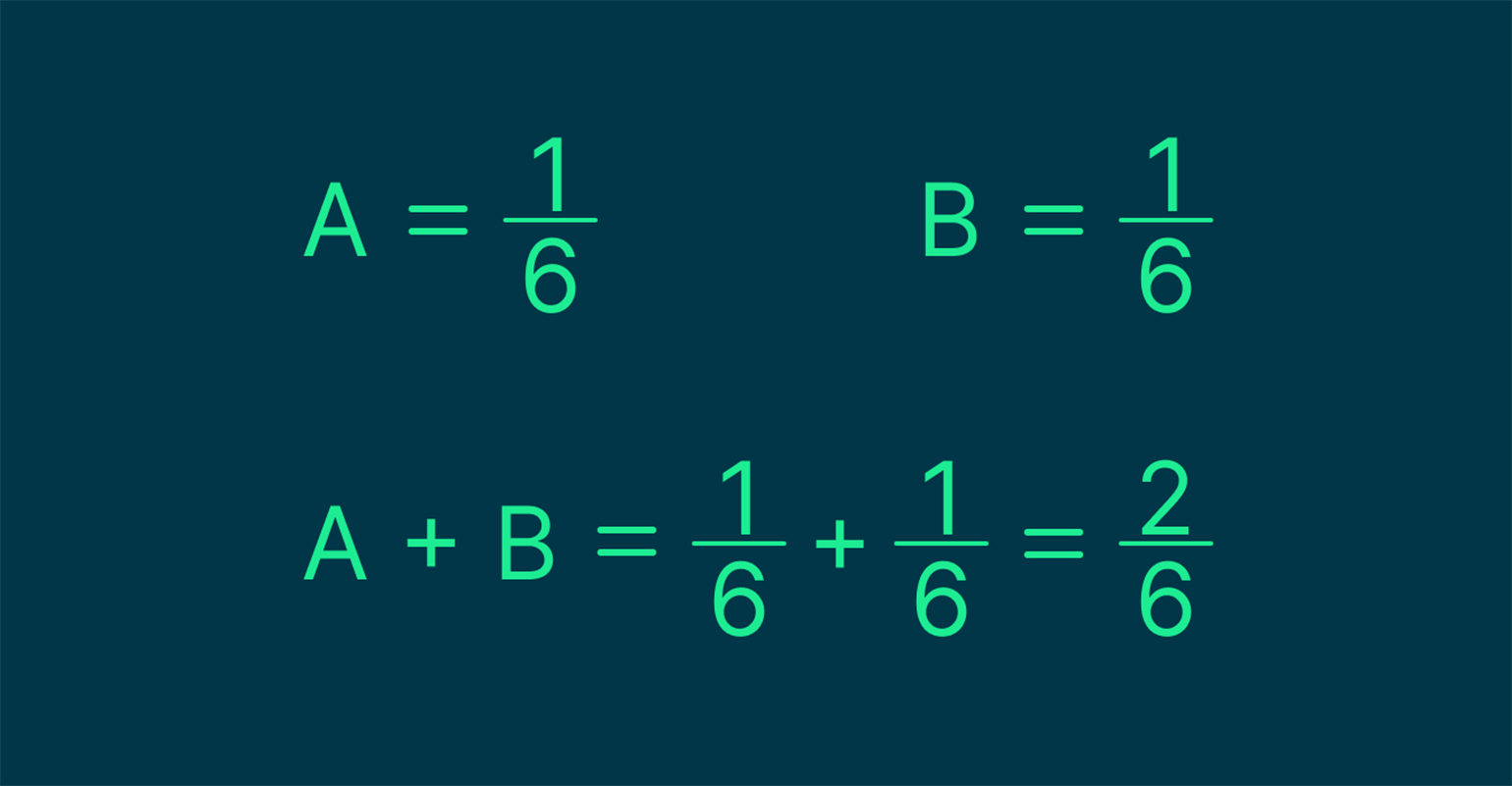
Получается, что шанс выпадения стороны 2 или 4 при броске кубика равен 2 к 6, или 1 к 3, или 33%.
Правило сложения можно применять не только к двум событиям, но и к любому их количеству. Например, событие A + B + C + D произойдёт, если случится хотя бы одно из событий A, B, C, D или одна из их комбинаций, такая как A и C или A, C и D.
Умножение (пересечение) событий
Произведение событий A и B — это событие A × B, которое произойдёт, если случится и событие A, и событие B.
Допустим, мы бросаем монетку два раза и хотим понять, каков шанс, что оба раза выпадет решка. Напомним, что вероятность выпадения решки — 1/2.
Обозначаем события: A — решка выпадает первый раз, B — решка выпадает второй раз. Считаем вероятности:
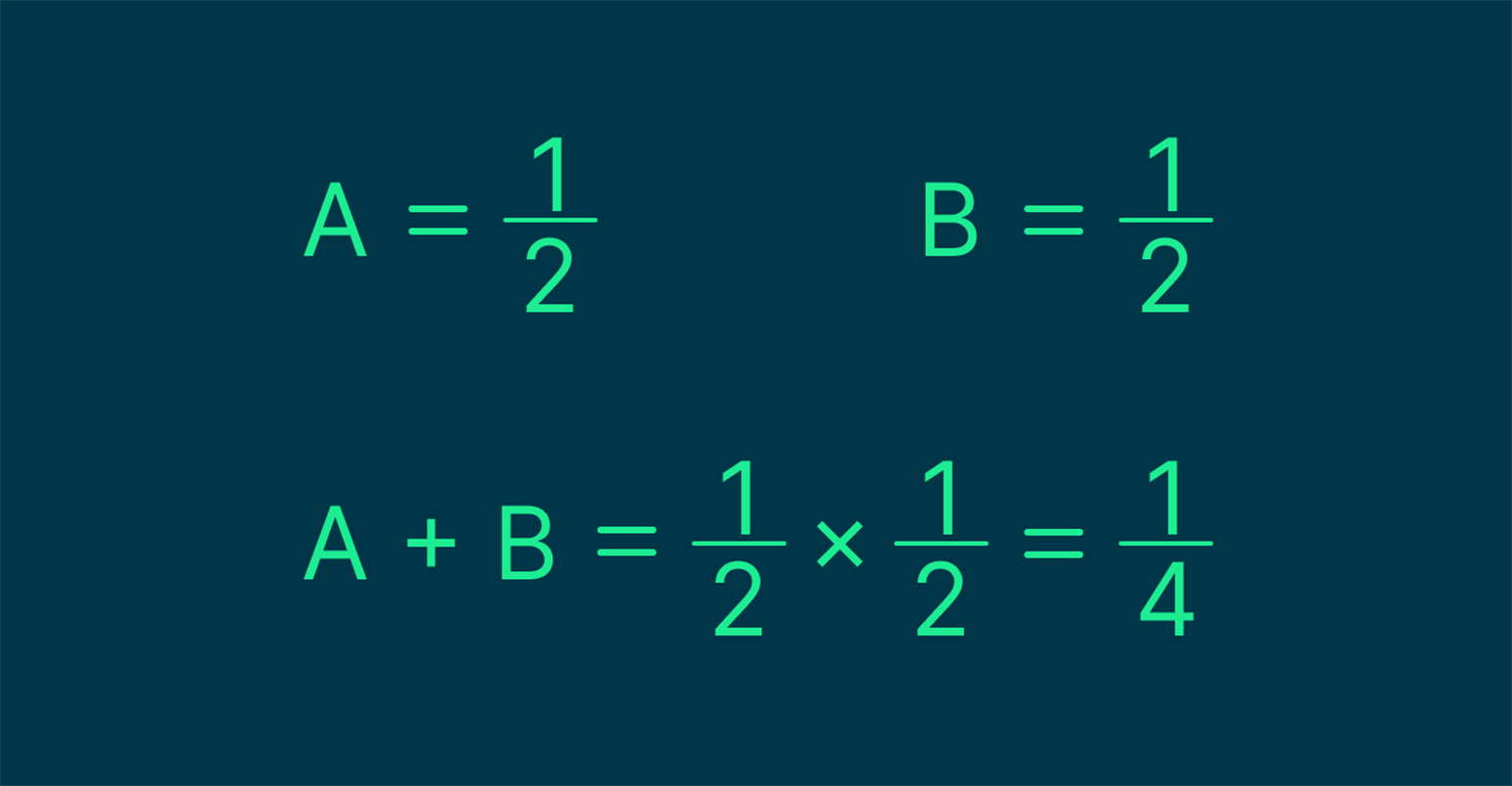
Получаем, что шанс выпадения решки два раза подряд — 25%.
Как в случае с суммой, произведение событий можно считать для любого количества разных событий. Давайте продолжим пример с монеткой — теперь мы хотим, чтобы она выпала четыре раза подряд.
Добавляем два новых обозначения: C — решка выпадает третий раз, D — решка выпадает четвёртый раз. Вероятности всё те же, считаем их произведение:
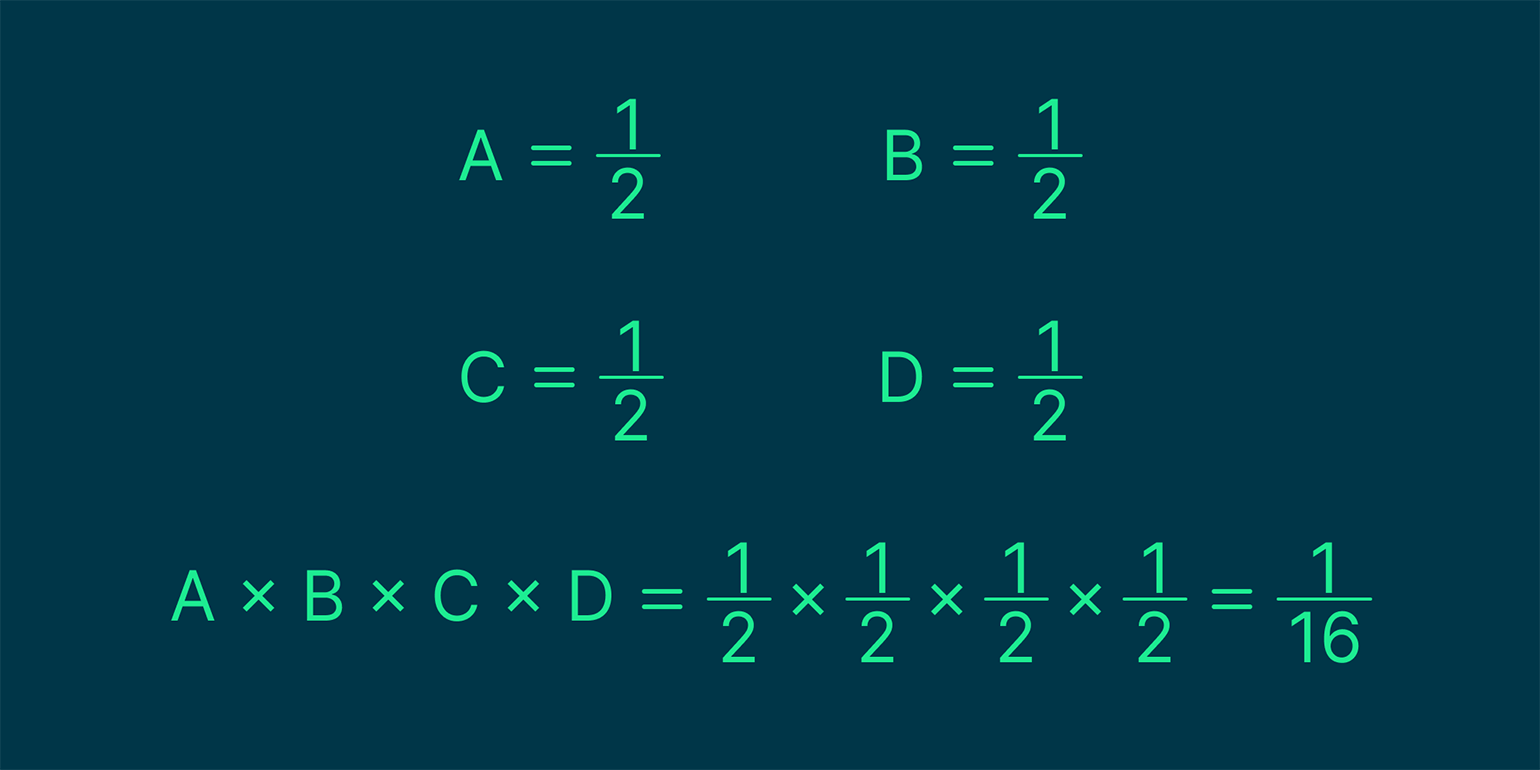
Ответ — шанс выпадения решки четыре раза подряд равен 1 к 16, или 6,25%.
Сложение совместимых событий
Когда мы говорили о сложении вероятностей, мы использовали несовместимые события, поскольку при броске кубика может выпасть только одна сторона (или ребро, если вам сильно повезёт).
Теперь, когда мы познали тонкости вероятностного умножения, можно разобраться с тем, как складывать совместимые события. В этом случае из суммы двух событий нужно просто вычесть их произведение. Формула выглядит так:
P (A + B) = P (A) + P (B) — P (A ⋅ B)
Примером такого сложения может быть выбор случайных чисел. Допустим, у нас есть набор чисел от 1 до 10 и мы хотим найти вероятность того, что выбранное число будет или нечётным, или делиться на 7 без остатка.
Считаем вероятности:
- Событие A — число нечётное. Вероятность выбрать именно его — 5/10.
- Событие B — число делится на 7 без остатка. Вероятность — 1/10.
Так как число 7 удовлетворяет обоим условиям, мы имеем дело с совместимыми событиями — то есть они могут происходить одновременно. Подключаем формулу: сначала находим сумму вероятностей, а потом вычитаем из неё вероятность пересечения. Внимание на экран:
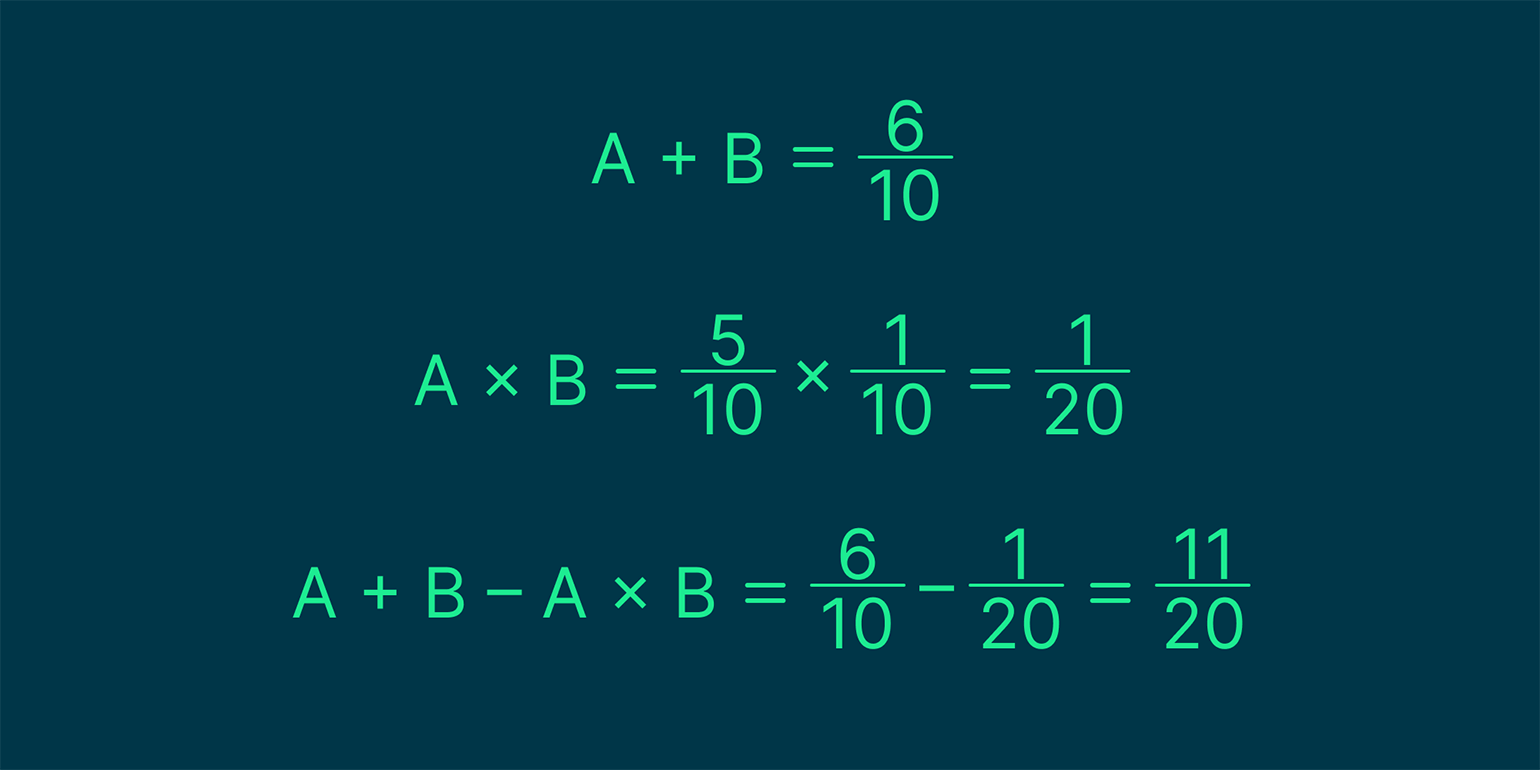
Вуаля! Получается, что шанс выполнения одного из двух событий равен 11/20, или 55%.
На этом с алгеброй событий закончим и перейдём к более классическим формулам. Но не пугайтесь, мы всё подробно объясним.
Ещё несколько формул теории вероятностей
Для начала — универсальная формула. Выглядит она так:
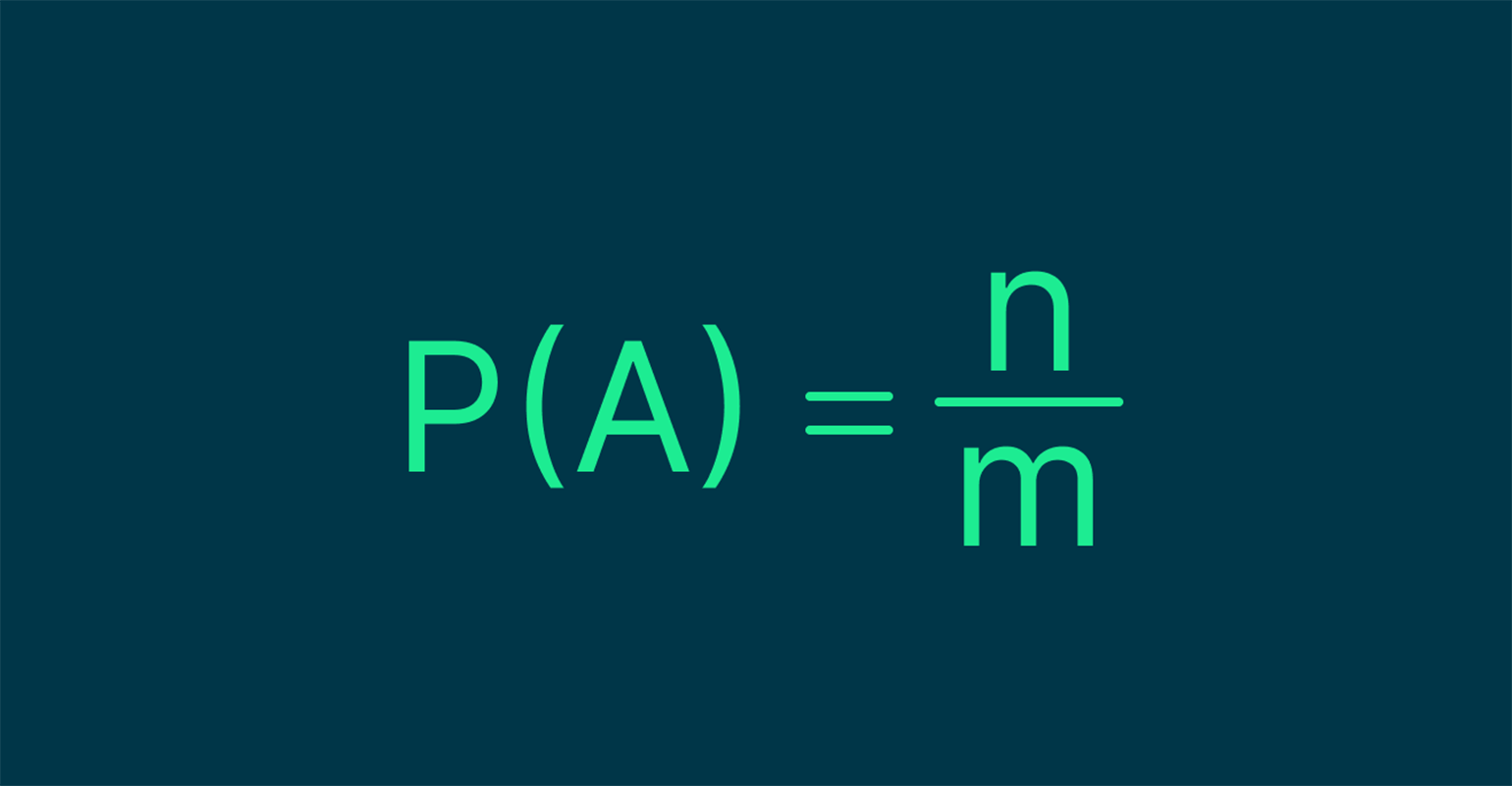
Разберёмся, что значат все эти буквы:
- Функция P вычисляет вероятность того, что произойдёт событие, которое нас устраивает (A);
- m обозначает общее число возможных событий;
- n — число благоприятных исходов.
Например, попробуем вычислить по этой формуле вероятность выпадения решки:

Всё в порядке, формула работает.
Давайте усложним задачу: посчитаем вероятность того, что решка выпадет три раза. Для этого нужно разбить событие на несколько уникальных — например, выпадение решки при первом, втором и третьем бросках. Обозначим эти события как B, C и D.

Так как эти события зависимы друг от друга, нам нужно их перемножить — для этого подставляем в нашу формулу числа:
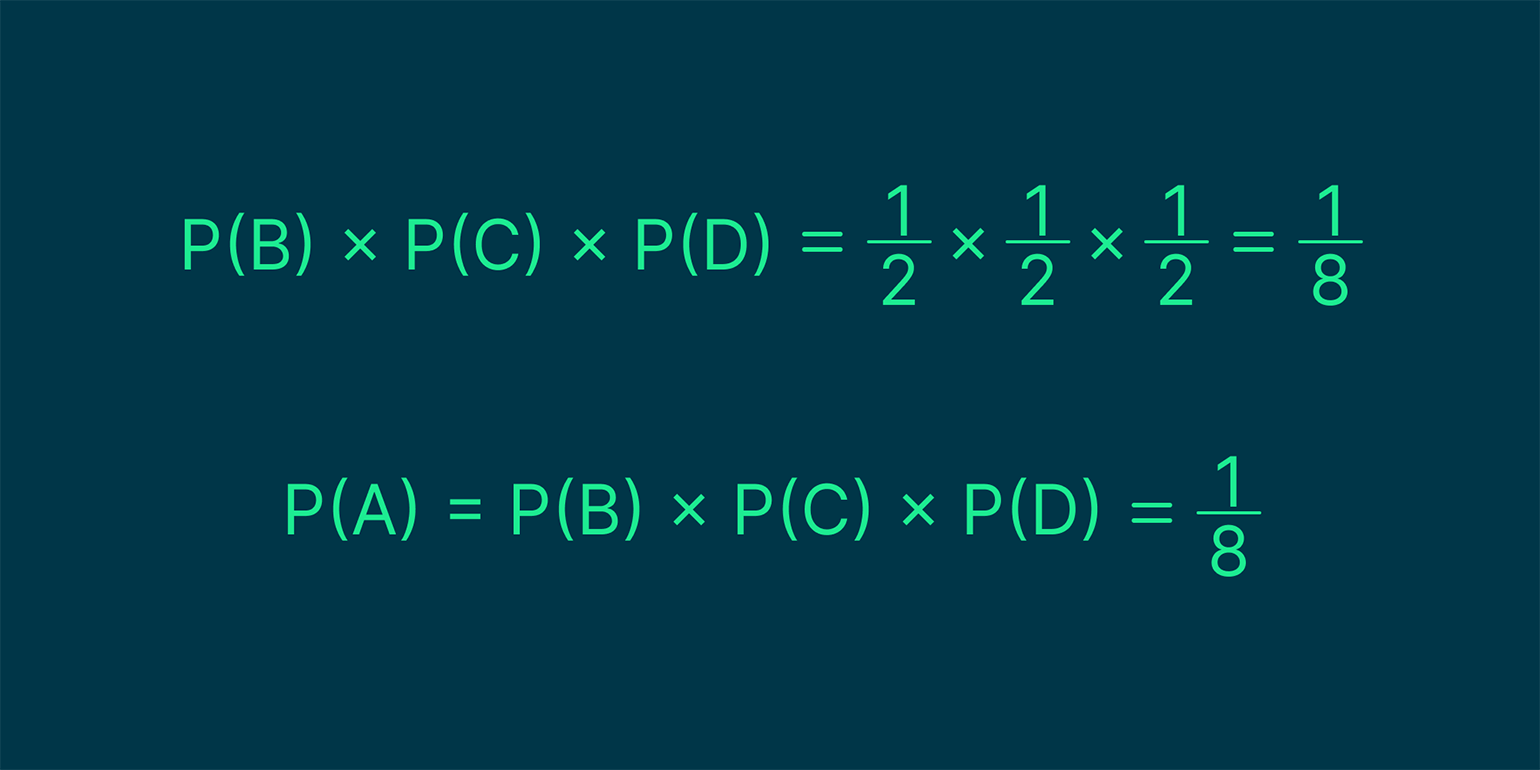
Всё верно — вероятность посчитали правильно.
Из этой формулы можно сделать несколько выводов:
- Если вероятность равна единице — значит, она достоверная. Смысл в том, что из общего числа событий нам подходят все — то есть событие точно произойдёт.
- Если вероятность равна нулю — значит, она невозможная. Всё из-за того, что нам не подходит ни одно из имеющихся событий.
- Если вероятность находится в диапазоне от нуля до единицы — она случайная. Это значит, что общее число результатов больше нуля, но не все из них нам подходят.
Теперь вы знаете достаточно, чтобы решать простые задачи по теории вероятностей, чем мы и займёмся в следующем разделе.
Решаем задачи по теории вероятностей
При решении задач используйте главную формулу теории вероятностей, а также формулы сложения и произведения вероятности событий.
Задача 1. В колоде 52 карты. Мы решили вытащить из неё одну — найдите вероятность того, что это будет туз.
Решение:
Расклад такой:
- Число всех возможных событий — 52, так как в колоде 52 карты.
- Число благоприятных событий — четыре, так как всего в колоде четыре туза.
Вычислим вероятность того, что из всех карт нам попадётся именно туз:

Теперь посчитаем сумму благоприятных событий:

Ответ: 4/52, или 1/13.
Задача 2. В кармане лежит шесть монет: две рублёвых, две пятирублёвых и две десятирублёвых. Мы по очереди достаём две из них случайным образом. Найдите вероятность того, что они обе будут одного номинала.
Решение:
Сначала мы достаём первую монету. Это может быть или рубль, или пять, или десять. Получается, вероятность достать монету любого номинала — 1/3.
Теперь достаём вторую монету — она должна быть того же номинала, что и первая. Так как только одна из них удовлетворяет нашим критериям, вероятность этого составляет 1/5. А так как наши события связаны друг с другом, перемножаем вероятности обоих:

Ответ: 1/15.
Задача 3. Вы бросаете игральные кости с шестью сторонами. Найдите вероятность того, что сумма выпавших очков будет равна 7.
Решение:
Всего существует шесть различных комбинаций, которые дают сумму 7:
- 1 — 6;
- 2 — 5;
- 3 — 4;
- 4 — 3;
- 5 — 2;
- 6 — 1.
Общее число возможных результатов при бросании двух костей равно 6 × 6 = 36. Подставляем наши значения в формулу:

Ответ: 6/36, или 1/6.
Что дальше
В этой статье мы разобрались с базовыми понятиями теории вероятностей. Если хотите лучше разбираться в вопросе, хорошие лекции можно найти здесь и здесь. А на этом бесплатном курсе теория даётся сразу с примерами и упражнениями — полезно, если хотите отточить знания на практике.
Для общего развития можно почитать нашу статью «Математика для джунов» и статью о том, как устроена случайность в играх. А если вы всерьёз нацелены вкатиться в data science и хотите подтянуть математический бэкграунд, для вас есть курс «Основы математики для Data Science».
Data Science с нуля: пробуем профессии на практике за 5 дней
Вы разберётесь в трёх главных направлениях data science: машинном обучении, разработке на Python и визуализации данных. Решите, какая сфера вам ближе, и выполните 4 реальные задачи с данными.
Пройти бесплатно







