Производные для чайников: учимся измерять скорость изменения функции
Погружаемся в основы дифференциального исчисления.

При создании игр разработчики используют дифференциальное исчисление для моделирования движения персонажей. Например, когда персонаж прыгает или бросает предмет, оно помогает рассчитать траекторию с учётом скорости, ускорения и других факторов. Это позволяет создать реалистичную физику и более естественное поведение объектов.
Дифференциальное исчисление — это раздел математического анализа, который изучает скорость изменения функций и их производные. Такое исчисление широко используется в физике, экономике, инженерии и других областях для моделирования и анализа динамических процессов.
Одной из ключевых концепций дифференциального исчисления являются производные функции. Из этой статьи вы узнаете, что они собой представляют, какой у них смысл и как их правильно вычислять.
Содержание
- Что такое производная
- В чём смысл производной
- Таблица производных функции
- Как найти значение производной
Что такое производная функции и зачем она нужна
Чтобы понять тему производной функции, давайте сначала вспомним понятие функции. Представьте, как вы катаетесь на велосипеде: разгоняетесь, тормозите и едете с постоянной скоростью. Скорость велосипеда меняется с течением времени — это и есть пример функции времени.
Функция — это математическое правило, которое принимает на вход число (аргумент) и возвращает определённый результат. В нашем примере результатом будет скорость велосипеда, а аргументом — время движения.
Если представить зависимость скорости от времени в виде формулы, она примет следующий вид: V = f(t). Распишем значения этой формулы:
- Скорость велосипеда (V) — зависимая переменная, которая изменяется с течением времени. Например, в начале поездки она может быть 0 км/ч, через 5 минут — 20 км/ч, а через 10 минут — 30 км/ч.
- Время (t) — независимая переменная, которую мы задаём самостоятельно. Она служит аргументом функции.
- Функция f(t) описывает зависимость скорости от времени. Например,
f(t) = 3t + 2. Эта функция означает, что каждую минуту скорость увеличивается на 3 км/ч, начиная с 2 км/ч в момент старта. Получается, через 5 минут скорость будет равна 3 × 5 + 2 = 17 км/ч.
Построим график изменения скорости велосипеда в двумерной системе координат X и Y. По горизонтальной оси X будем откладывать время движения, а по вертикальной оси Y — скорость велосипеда:
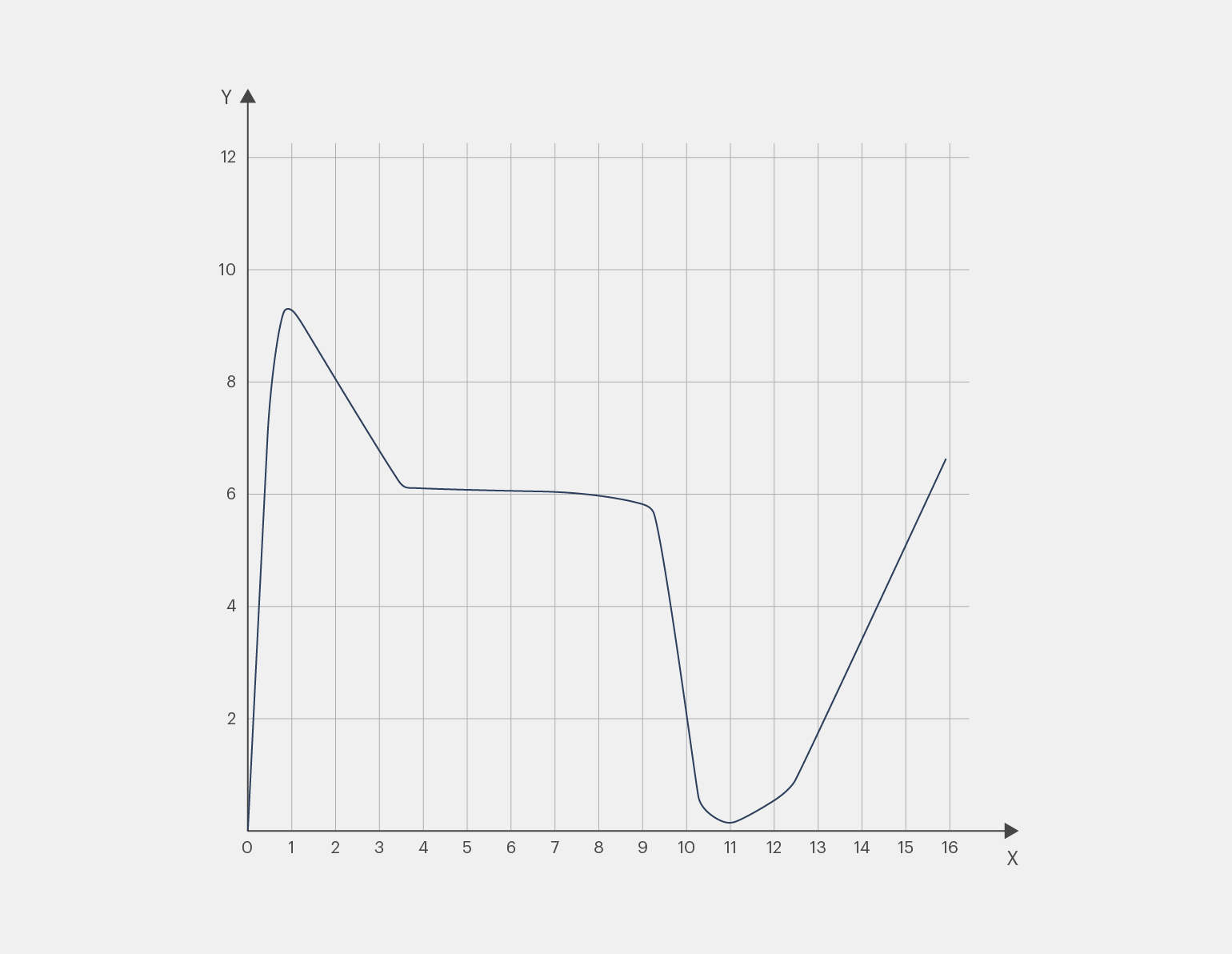
Инфографика: Майя Мальгина для Skillbox Media
Мы вспомнили понятие функции, и теперь давайте рассмотрим изменение скорости велосипеда в разные промежутки времени. Для этого разберём два понятия: приращение аргумента и приращение функции.
Отметим на графике точки A и B, опустим из них перпендикуляры на оси X и Y. Точки пересечения этих перпендикуляров с осями будут координатами точек A и B. Пусть точка A имеет координаты (x₁, y₁), а точка B — (x₂, y₂):
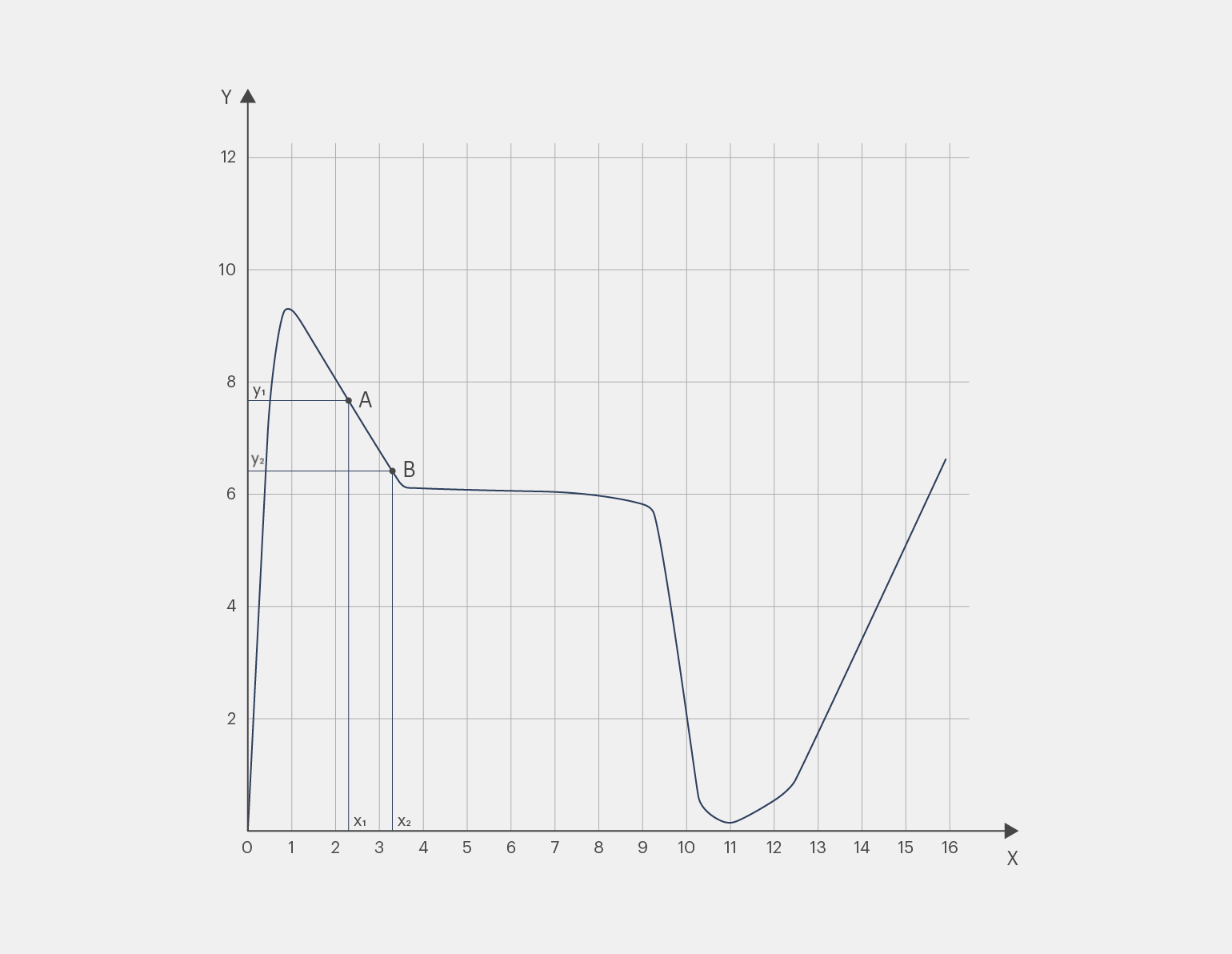
Инфографика: Майя Мальгина для Skillbox Media
На графике в момент времени x₁ скорость велосипеда равна y₁, а в момент времени x₂ она становится равной y₂. За промежуток времени Δx = x₂ − x₁ скорость изменяется на следующую величину Δy = y₂ − y₁.
Разность между двумя значениями аргумента называется приращением аргумента. В нашем случае это изменение времени между двумя точками измерения скорости: если мы измеряем скорость в начале движения и через 5 минут, приращение аргумента составит 5 минут. В системе координат XY оно обозначается как Δx, где Δ (дельта) — символ приращения.
С изменением аргумента изменяется и сама функция. Это изменение называется приращением функции. В нашем примере это изменение скорости между двумя точками измерения. Например, если скорость в начале движения была 0 км/ч, а через 5 минут стала 20 км/ч, приращение функции составит 20 км/ч. В системе координат XY оно обозначается как Δy.
Для функции y = f(x) приращение будет равно Δy = f(x + Δx) − f(x):
- f(x) — значение функции в исходной точке;
- f(x + Δx) — значение функции в точке, смещённой на Δx;
- Δx — приращение аргумента;
- Δy — приращение функции.
Приращение аргумента и приращение функции позволяют определить скорость изменения функции. Это помогает понять динамику движения велосипеда в любой момент времени. Если скорость изменения функции положительная — велосипед ускоряется, если отрицательная — замедляется, а если равна нулю — движется с постоянной скоростью.
Скорость изменения функции относительно изменения её аргумента вычисляется как отношение приращения функции к приращению аргумента. Точность этого значения увеличивается при уменьшении приращения аргумента. Для наиболее точного результата необходимо рассматривать это отношение при малых изменениях аргумента.
Представьте, что нам нужно узнать скорость велосипеда в конкретный момент, а не среднюю скорость за некоторый промежуток времени. Для этого нужно рассмотреть такой короткий интервал времени, что он почти сводится к точке. В математике это выражается через понятие предела. Вот именно здесь мы и сталкиваемся с понятием производной функции.
Производная — это предельное значение скорости изменения функции при стремлении изменения аргумента к нулю. То есть это мгновенная скорость изменения функции в заданной точке. Вот формула производной:
Элементы формулы:
- f'(x) — производная функции f в точке x;
- lim — предел выражения при стремлении Δx к нулю;
- Δx — приращение аргумента;
- f(x + Δx) — значение функции в точке x + Δx;
- f(x) — значение функции в точке x.
В примере с велосипедом производная функции скорости по времени показывает мгновенное ускорение. Это значение позволяет:
- Определять, как быстро изменяется скорость велосипеда в любой момент времени.
- Понять, когда велосипедист ускоряется, замедляется или движется с постоянной скоростью.
- Рассчитать время для достижения определённой скорости.
- Оптимизировать маршрут, учитывая изменение скорости на разных участках пути.
В следующем разделе мы ещё обсудим предназначение производной, когда на примерах будем рассматривать её физический смысл.
Геометрический и физический смысл производной
Геометрический и физический смысл производной — это два различных подхода, позволяющие понять значение этого математического понятия.
Геометрический смысл производной можно понять через график функции. Рассмотрим график y = f(x). Отметим на нём точки A (x₁, y₁) и B (x₂, y₂), а затем проведём из них перпендикуляры к осям X и Y. Если теперь мы соединим точки A и B, то образуем прямоугольный треугольник ABC.
В этом треугольнике отношение приращения функции Δy к приращению аргумента Δx равно тангенсу угла ABC, который образован секущей линией AB и положительным направлением оси X. Если мы начнём сближать точки x₁ и x₂, расстояние между ними (Δx) также будет уменьшаться, пока секущая постепенно не превратится в касательную — прямую, соприкасающуюся с графиком функции в одной точке.
Эта касательная и определяет значение производной в данной точке. Поэтому геометрический смысл производной можно сформулировать так: значение производной функции в точке x₀ равно тангенсу угла наклона касательной к графику функции в этой точке.
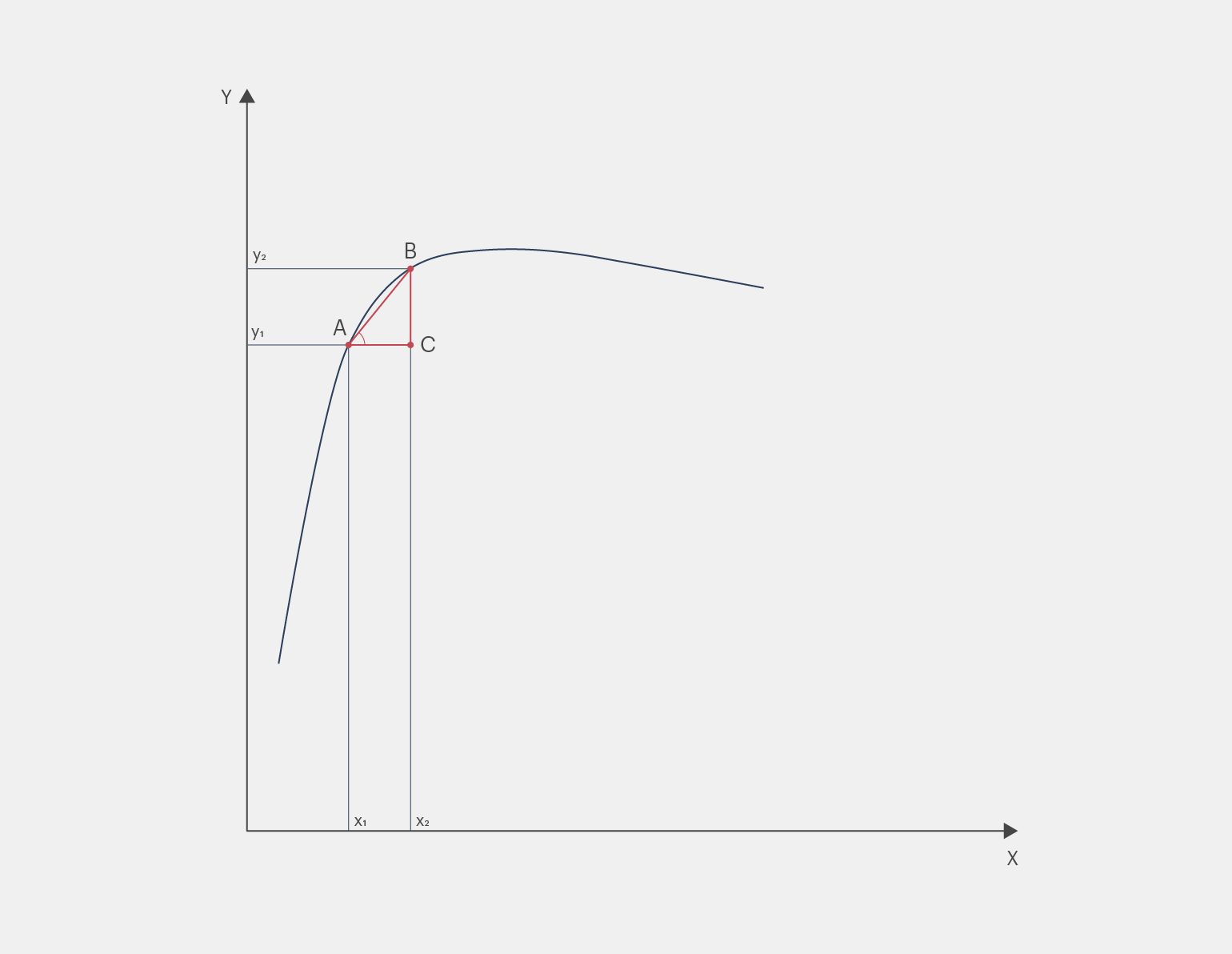
Инфографика: Майя Мальгина для Skillbox Media
Рассмотрим, как меняется производная для различных типов функций, чтобы лучше понять, как она отражает поведение функции на графике. Разберём три основных случая: возрастающую функцию, убывающую функцию и функцию в точке экстремума.
Производная возрастающей функции. У возрастающей функции значения y увеличиваются с увеличением x. Производная такой функции всегда положительна: f′(x) > 0. Это означает, что у касательной к графику функции положительный наклон, а график функции направлен вверх.
Производная убывающей функции. У убывающей функции значения y уменьшаются с увеличением x. Производная убывающей функции всегда отрицательна: f′(x) < 0. В этом случае наклон касательной отрицательный, а график функции направлен вниз.
Производная в точке экстремума. Экстремум — это точка, в которой функция достигает локального максимума или минимума. В этой точке производная функции равна нулю: f′(x) = 0. Это означает следующее:
- В точке локального максимума функция меняет направление с возрастающей на убывающую.
- В точке локального минимума функция меняет направление с убывающей на возрастающую.
Анализ производной функции помогает понять её поведение. Представьте, что вы едете на велосипеде по холмистой местности. График вашего пути можно интерпретировать как функцию, где ось X — это пройденное расстояние, а ось Y — высота над уровнем моря.
Рассмотрим производную на разных участках пути:
- Когда вы поднимаетесь в гору, производная положительна — функция возрастает.
- Когда вы спускаетесь с горы, производная отрицательна — функция убывает.
- На вершине холма или в низине долины производная равна нулю — это точки экстремума.
Значение производной в каждой точке отображает крутизну подъёма или спуска. И чем больше абсолютное значение производной, тем круче склон.
Теперь рассмотрим физический смысл производной — её интерпретацию в контексте реальных процессов и явлений. Производная позволяет точно описать, как быстро изменяется одна физическая величина относительно другой во времени или в зависимости от иных параметров.
Вот несколько примеров:
- Сила тока — производная электрического заряда по времени. Она характеризует скорость прохождения заряда через проводник: чем быстрее проходит заряд, тем больше сила тока.
- Скорость нагрева или охлаждения тела — это производная температуры по времени. Она отражает интенсивность изменения температуры объекта: чем быстрее меняется температура, тем выше скорость нагрева или охлаждения.
- Предельная прибыль в экономике — производная общей прибыли по объёму производства. Она показывает, как изменяется общая прибыль при изменении объёма производства: чем выше предельная прибыль, тем выгоднее наращивать производство.
- Темп роста популяции — производная численности популяции по времени. Она показывает, как быстро изменяется количество особей в популяции: положительное значение указывает на рост, отрицательное — на сокращение численности.
- Скорость передачи данных — это производная объёма переданной информации по времени. Она определяет, как быстро передаётся информация: чем выше скорость, тем больший объём данных передаётся за единицу времени.
Производные для многих математических функций уже вычислены и собраны в таблице. Разберёмся, что это за таблица и как её использовать.
Таблица производных
Таблица производных — это справочный инструмент, содержащий производные основных математических функций: степенных, тригонометрических, показательных и логарифмических. Она помогает сэкономить время при решении задач на дифференцирование и позволяет быстро проверять правильность уже вычисленных значений.
В левом столбце таблицы находится исходная функция, а в правом — её производная. Для примера возьмём функцию f(x) = x² и найдём её производную по таблице:
- Функция f(x) = x² — это степенная функция со степенью n = 2.
- Используя формулу из таблицы для xⁿ, получаем: f'(x) = n · xⁿ⁻¹.
- Подставляем значение n = 2 в формулу: f'(x) = 2 · x²⁻¹ = 2 · x¹ = 2x.
Получается, производная функции x² равна 2x. Это означает, что скорость изменения функции x² в любой точке пропорциональна 2x.
| f(x) | f'(x) | Пояснение |
|---|---|---|
| c | 0 | Производная константы всегда равна нулю, так как константа не меняется. |
| x | 1 | Скорость изменения переменной x относительно самой себя всегда равна единице, независимо от значения x. |
| xⁿ | n · xⁿ⁻¹ | Степень уменьшается на 1, а коэффициент умножается на начальную степень. |
| √x | 1 / (2√x) | Это частный случай степенной функции, где n = 1/2. |
| sin x | cos x | Производная синуса равна косинусу. |
| cos x | —sin x | Производная косинуса — это минус синус. |
| tg x | 1 / cos²x | Производная тангенса выражается через квадрат косинуса. |
| ctg x | −1 / sin²x | Производная котангенса выражается с минусом через квадрат синуса. |
| eˣ | eˣ | Экспонента — единственная функция, равная своей производной. |
| ln x | 1 / x | Производная натурального логарифма обратно пропорциональна x. |
Таблица производных охватывает только основные функции. Для более сложных выражений необходимо выполнять расчёты самостоятельно, используя правила дифференцирования сложных функций.
Правила нахождения производной функции
Правила дифференцирования — это принципы, позволяющие находить производные сложных функций путём разложения их на более простые составляющие. Существует много таких правил, и для их углублённого изучения рекомендуются ресурсы Wolfram Alpha и Khan Academy. В этом разделе мы рассмотрим основные правила и разберём их на примерах.
Производная суммы функций равна сумме производных этих функций.
- Правило: (u + v)' = u' + v'
- Условие: y = x² + 3x
- Решение: y' = (x²)' + (3x)' = 2x + 3
Производная произведения функций. Производная произведения двух функций равна сумме произведений производной первой функции на вторую функцию и первой функции на производную второй функции.
- Правило: (u · v)' = u' · v + u · v'
- Условие: y = x · sin(x)
- Решение: y' = 1 · sin(x) + x · cos(x) = sin(x) + x · cos(x)
Производная частного двух функций представляется дробью. В числителе — разность произведений производной числителя на знаменатель и числителя на производную знаменателя. В знаменателе — квадрат знаменателя.
- Правило: (u/v)' = (u' · v − v' · u) / v²
- Условие: y = x / (x + 1)
- Решение: y' = (1 · (x + 1) − 1 · x) / (x + 1)² = 1 / (x + 1)²
Производная любой константы равна нулю.
- Правило: (c)' = 0
- Условие: y = 5
- Решение: y' = 0
Производная степенной функции. При дифференцировании степень уменьшается на единицу, а показатель степени становится множителем.
- Правило: (xⁿ)' = n · xⁿ⁻¹
- Условие: y = x³
- Решение: y' = 3x²
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!






