Пределы в математике: что это такое и как их решать

Предел функции — это одно из базовых понятий математического анализа. С пределом связаны такие термины, как непрерывность, производная и интеграл. Но самое главное — это мощный инструмент для анализа явлений в реальном мире. С его помощью анализируют производительность алгоритмов в информатике и рассчитывают нагрузки на несущие опоры мостов в строительстве.

Далее расскажем:

• что такое предел функции;
• как их решать;
• как избавиться от неопределённости в пределах;
• где найти короткие пути решения;
• что запомнить.

Что такое предел функции

Сначала вспомним, что такое функция и аргумент.

Функция — это математическое правило, которое получает на вход число и возвращает какой-то результат. Например, в функции y = x² число умножается на само себя. Передали 2, получили 4.

Аргумент — это число, которое мы передаём, то есть подставляем в функцию. В нашем примере аргумент равен 2.

В общем виде функция записывается так:

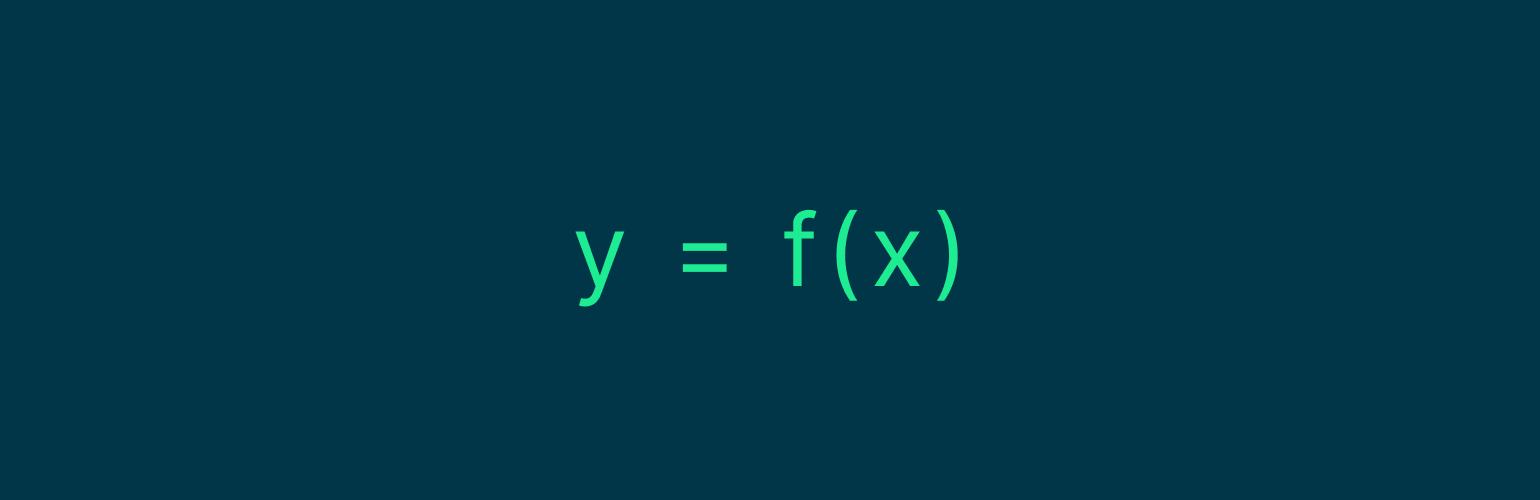
Здесь f — это функция, x — её аргумент, y — результат её выполнения.

Предел функции — это значение, к которому стремится функция, когда её аргумент приближается к определённому значению. Проще всего разобраться в этом на примере.

Напишем простую функцию:

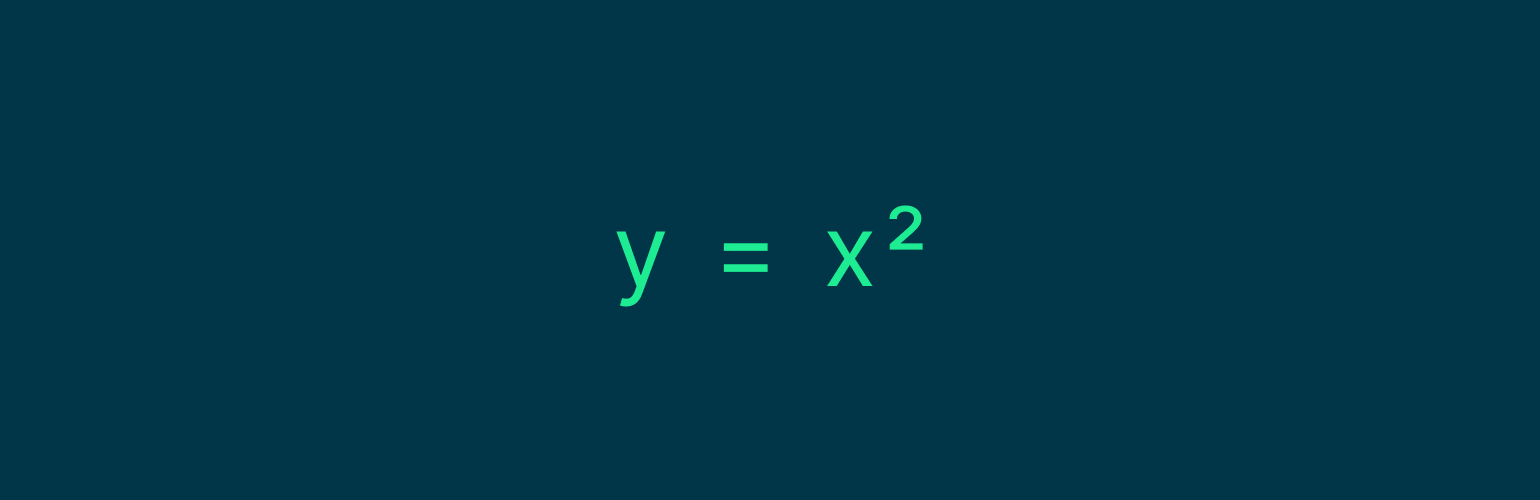
Представим, что x стремится к числу 2, но не достигает его:

1,9; 1,99; 1,999…1,99999.

Тогда y будет стремиться к 4:

3,61; 3,9601; 3,996001…3,9999600001.

Число будет всё больше и больше, но никогда не достигнет числа 4, а только приблизится к нему.

Получается, что предел для функции при x, стремящемся к 2, равен 4.

Предел в математике обозначается с помощью lim:

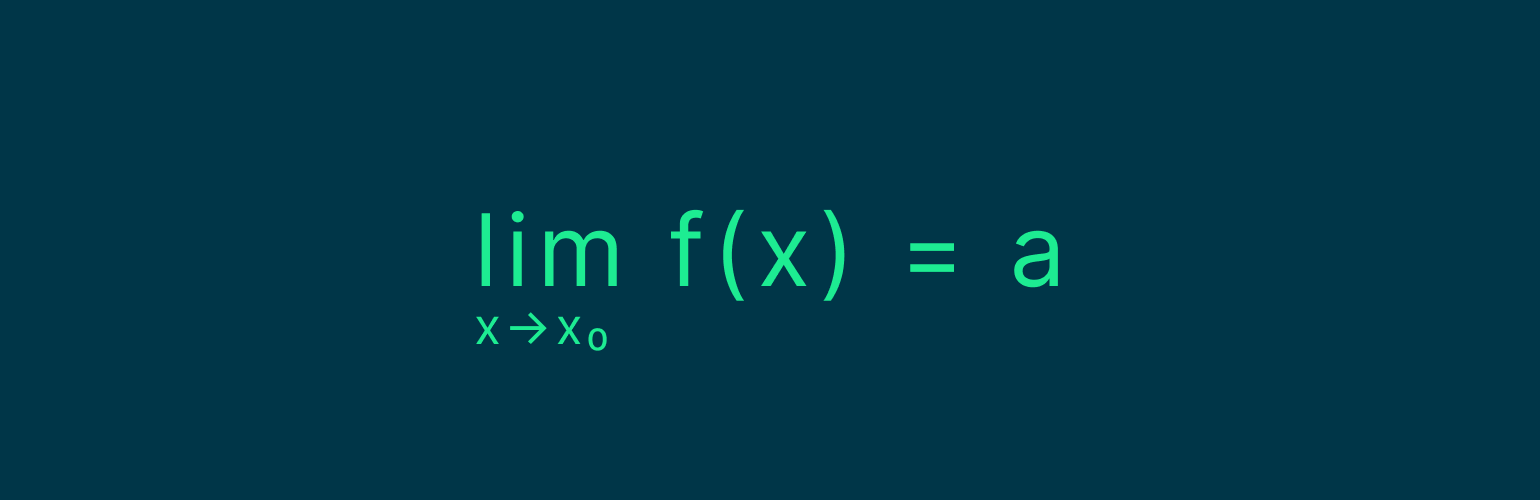
Читается выражение так: для функции y = f(x) пределом называется такое число a, к которому приближается y при x, стремящемся к определённой точке x₀. Стремление обозначается стрелкой.

Слово «стремится» означает, что переменная приближается к пределу на сколь угодно малую величину, но никогда не достигает его.

Посмотрим на другую формулу:

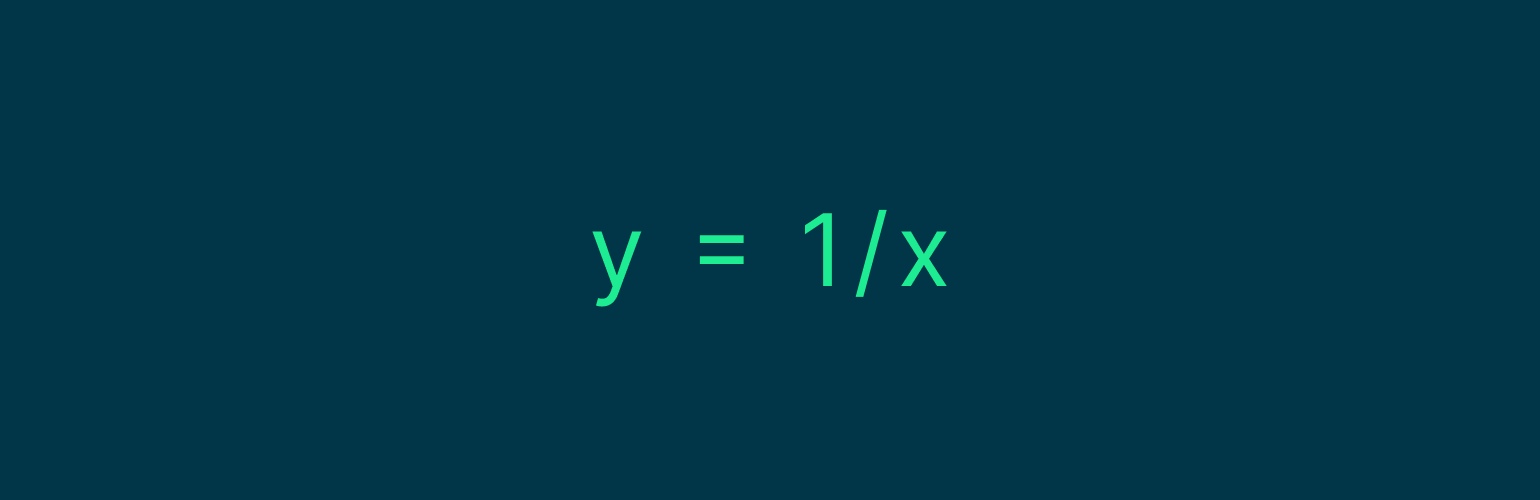
И сразу построим для неё график:

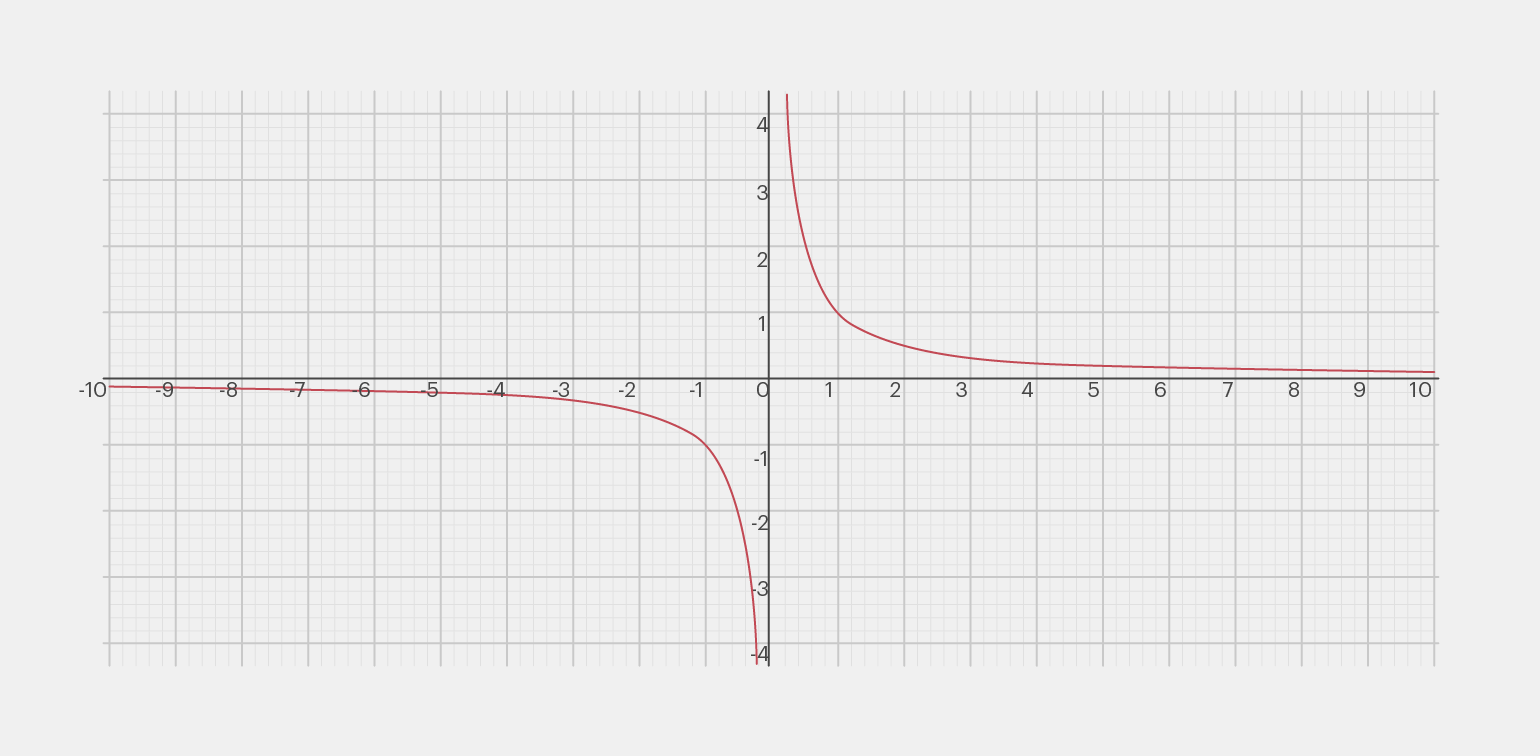
Мы видим, что чем больше становится значение x, тем ближе функция y = 1/x приближается к нулю, но при этом она никогда не достигнет его. То есть y не может стать равным 0.

Как решать пределы

Чтобы вычислить предел, во многих случаях достаточно подставить в функцию значение, к которому стремится её аргумент.

При возникновении неопределённостей, то есть отсутствия решения при подстановке числа, используются разные подходы: упрощение выражений с помощью деления многочленов на переменную в максимальной степени, умножение на сопряжённое выражение, правило Лопиталя и другие приёмы. О таких случаях мы подробно поговорим дальше.

Один из самых простых способов решения — использовать теоремы о пределах. Это математические правила, которые упрощают вычисления.

Например, предел функции y = c равен c при любом x.

Проверим на графике:

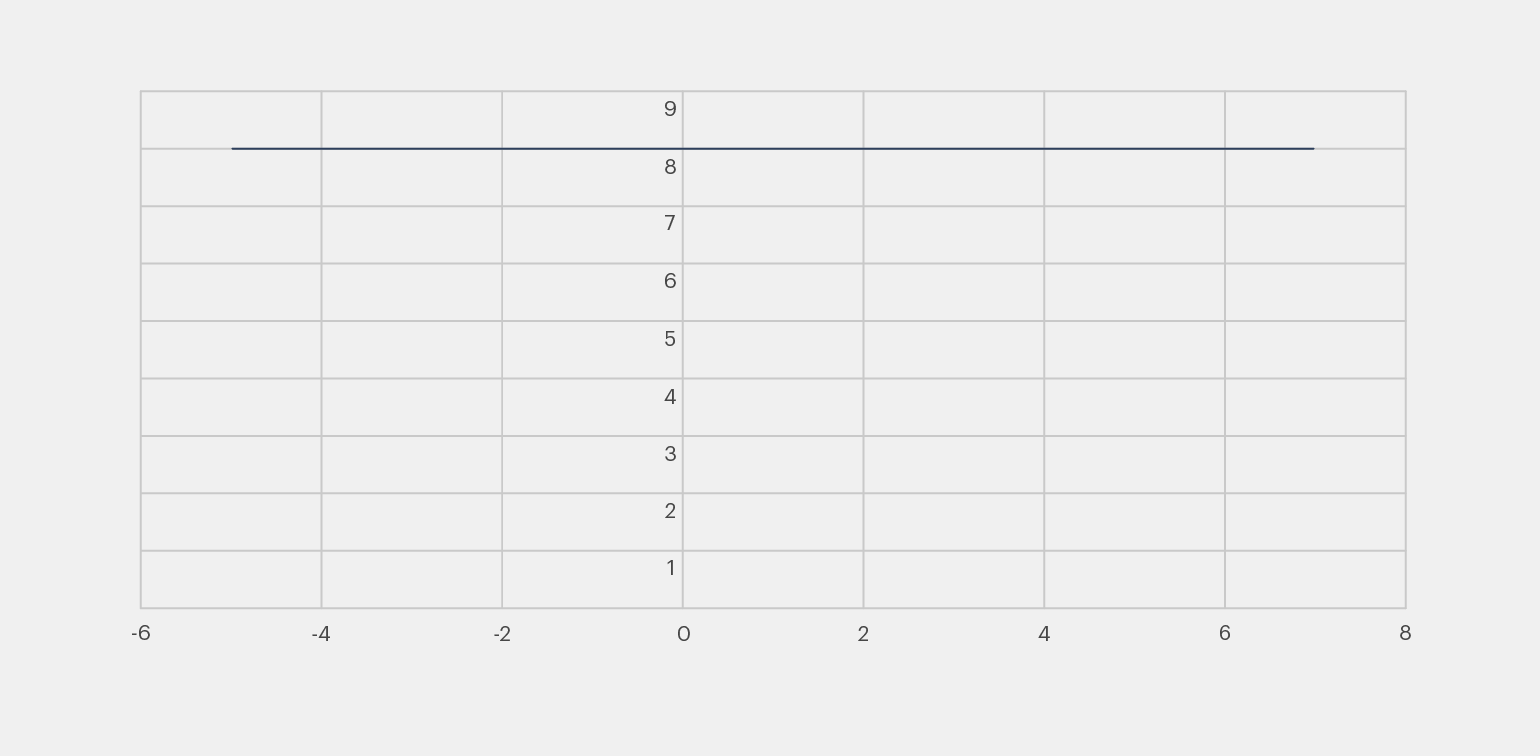
Как мы видим, при любом x функция принимает одно и то же значение: y = 8.

Существуют и другие теоремы для быстрого решения пределов:

• предел суммы нескольких функций равен сумме их пределов;
• предел произведения функций равен произведению их пределов;
• предел частного двух функций равен частному их пределов. Работает при условии, что знаменатель не обращается в ноль.

Некоторые задачи можно решить с помощью приведения к первому или второму замечательному пределу. В этом случае не нужно раскрывать содержащиеся в них неопределённости — это уже сделано и оформлено в готовый шаблон.

Но иногда от неопределённостей так легко не избавиться. Придётся достать тетрадь, ручку и вспомнить математику.

Неопределённости в пределах

Прежде чем перейти к неопределённости, вспомним, что такое непрерывные функции.

Непрерывность функции в точке означает, что в этой конкретной точке нет разрывов. Если говорить просто, то на построенном графике для неё в этой точке мы можем определить значение y по x.

Например, функция f(x) = 1/x имеет разрыв в точке x = 0. То есть в этой точке вычислить значение функции невозможно. Это хорошо видно на графике:

Мы видим, что для х = 0 значения y не существует — график не имеет точки с такой координатой.

Чтобы найти предел функции в любой точке непрерывности, достаточно просто подставить значение этой точки в функцию. Например, подставим 1 в f(x) = 1/x. Получаем:

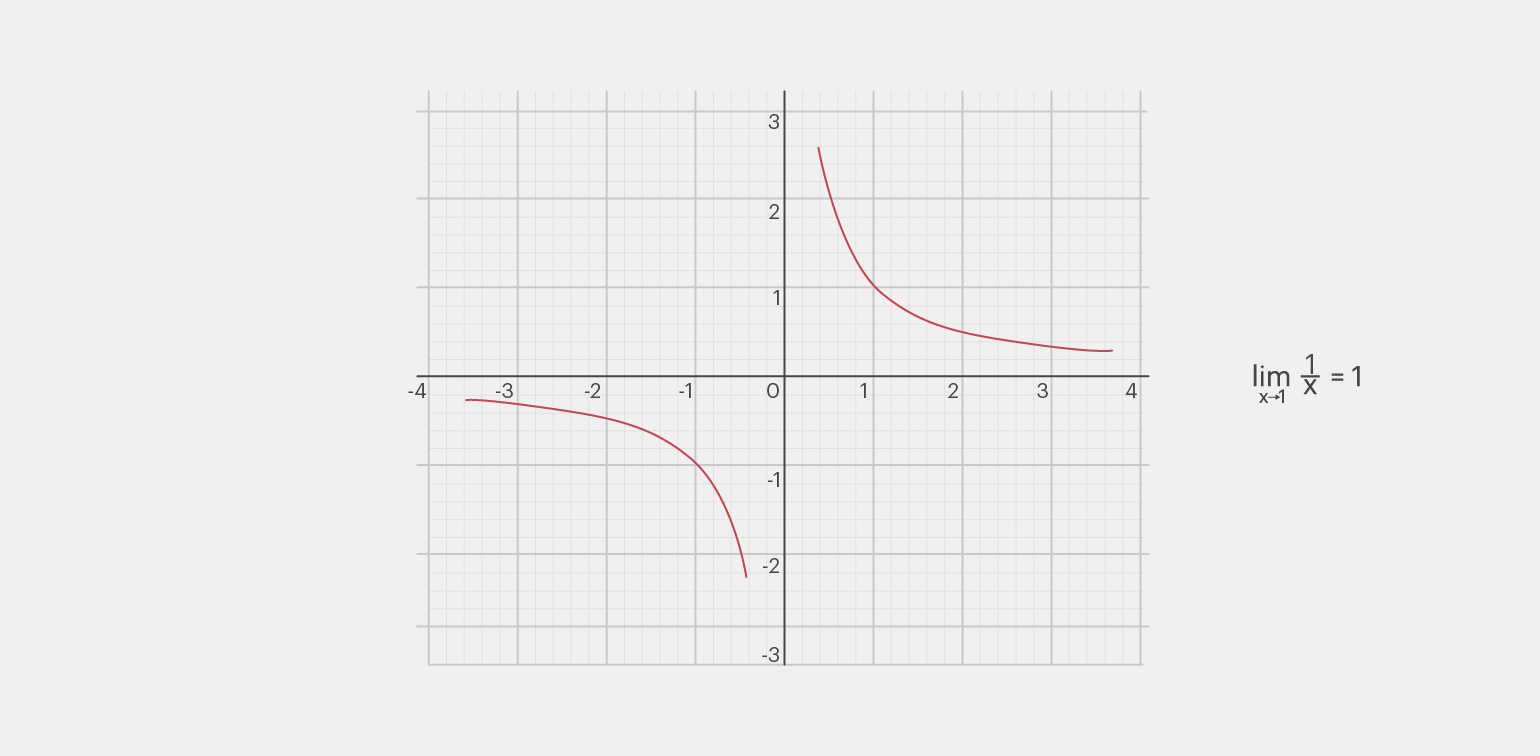
Предел в этом случае будет равен 1.

Но иногда такой способ решения приводит к неопределённости — то есть невозможности определить, существует ли предел функции в заданной точке и каково его значение.

Неопределённости бывают разных видов: ∞/∞ и 0/0.

Неопределённость ∞/∞

Рассмотрим функцию:

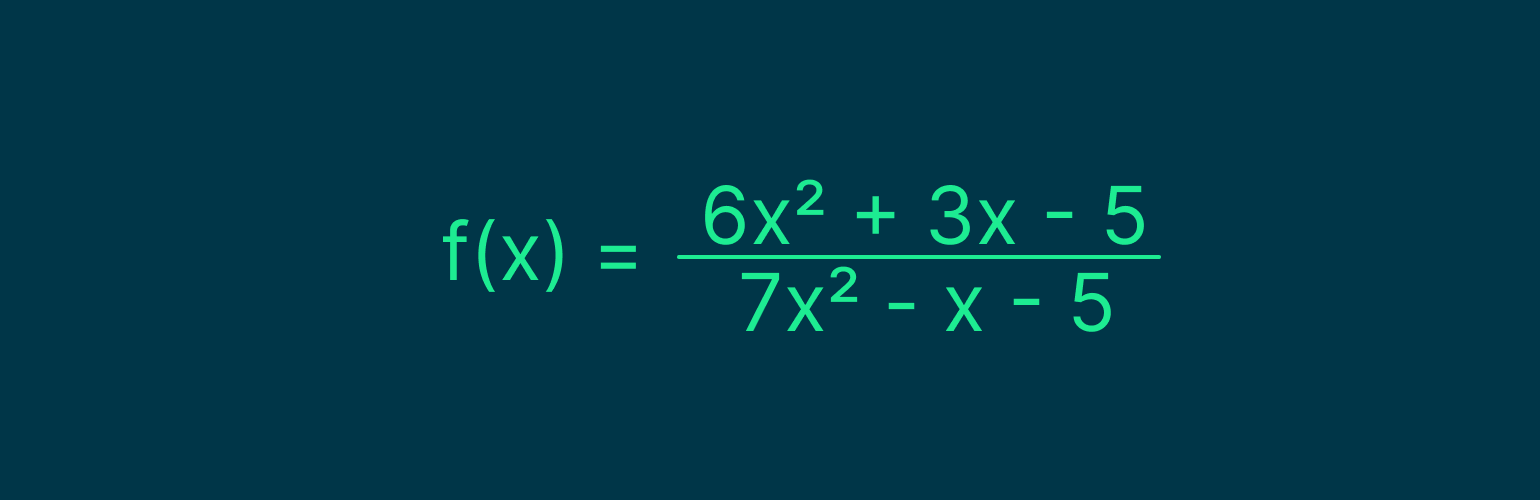
Найдём её предел при x, стремящемся к бесконечности.

Если мы подставим в формулу x, равный бесконечности, то получим в числителе и знаменателе бесконечность.

Бесконечность, делёная на бесконечность, — это неопределённость, так как результат деления может быть равен любому числу. Поэтому нам нужно от неё избавиться.

Для этого разделим числитель и знаменатель на x², то есть на переменную в старшей степени:

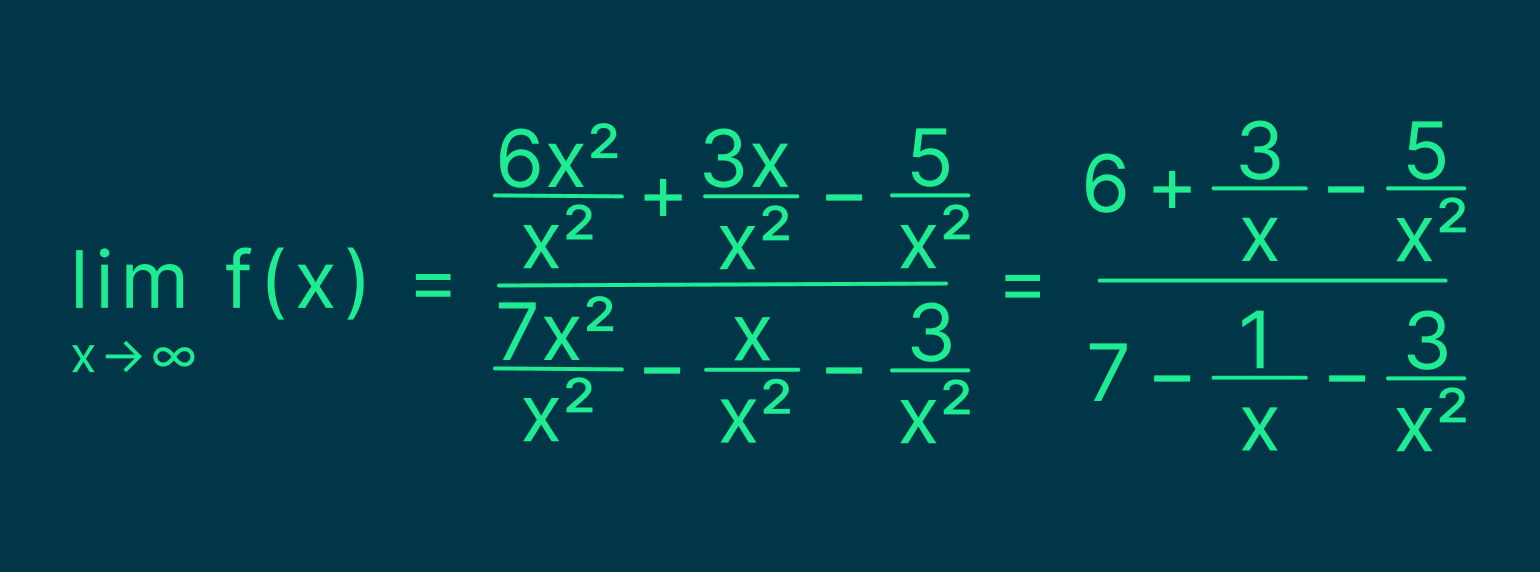
Теперь, если мы подставим бесконечность вместо х, то дроби с х в знаменателе превратятся в 0. В результате получим:

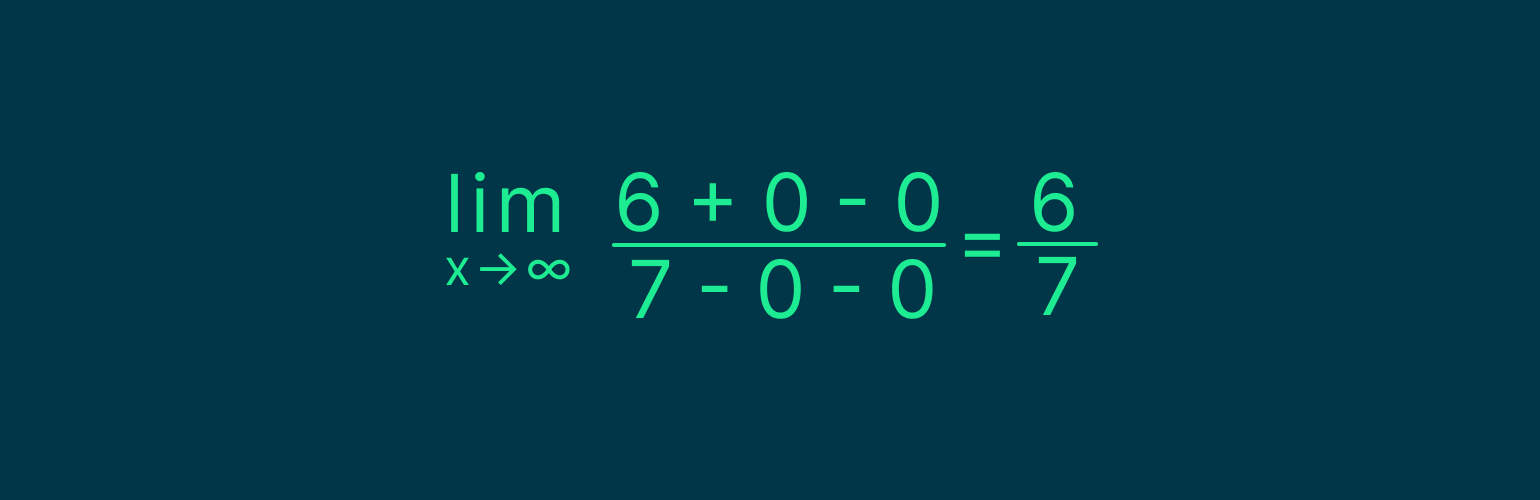
Таким образом, чтобы раскрыть неопределённость ∞/∞ в многочленах, нужно разделить числитель и знаменатель на переменную в старшей степени.

Неопределённость 0/0

Найдём предел функции:

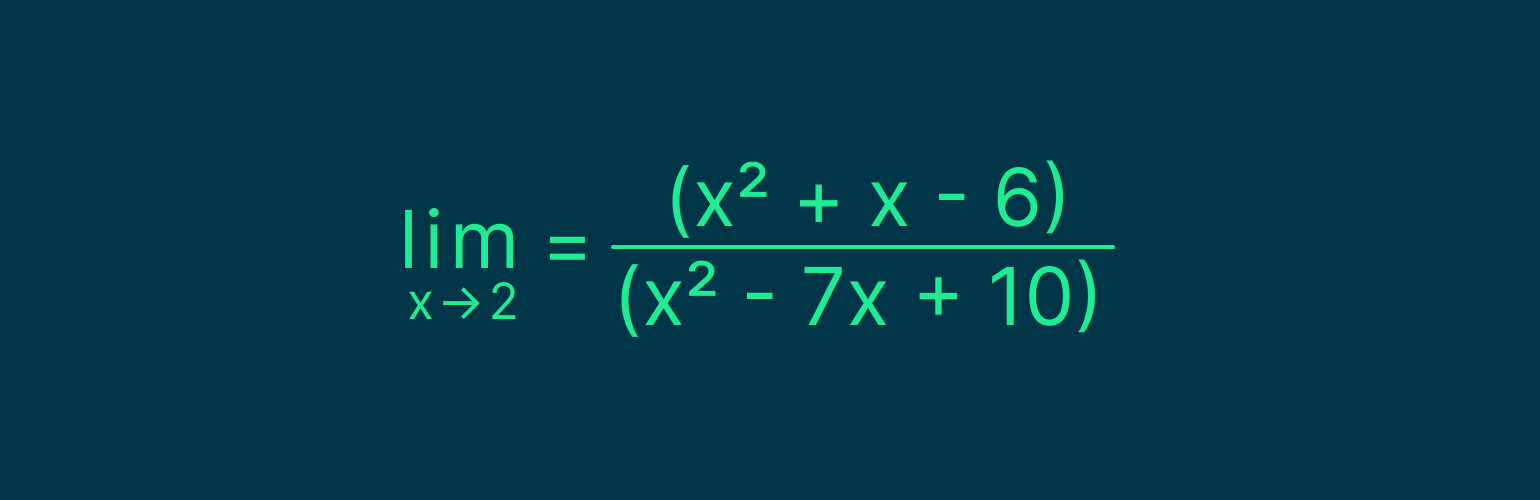
Если мы просто подставим в формулу x = 2, то в числителе и знаменателе получим 0.

Ноль, делёный на ноль, — это тоже неопределённость, которая может быть равна любому числу. Чтобы избавиться от неё, разложим числитель и знаменатель дроби на множители.

Числитель можно разложить так:

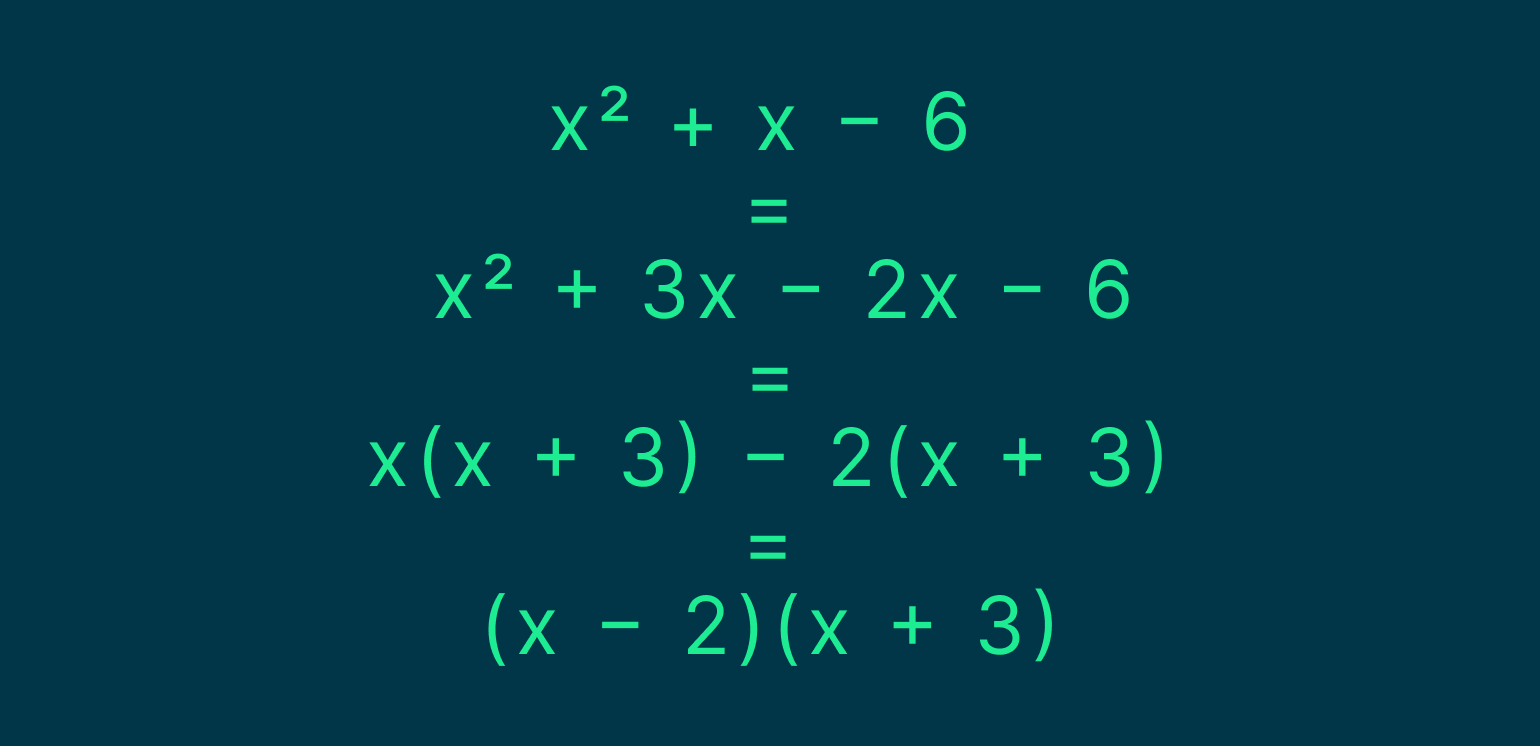
А знаменатель — так:

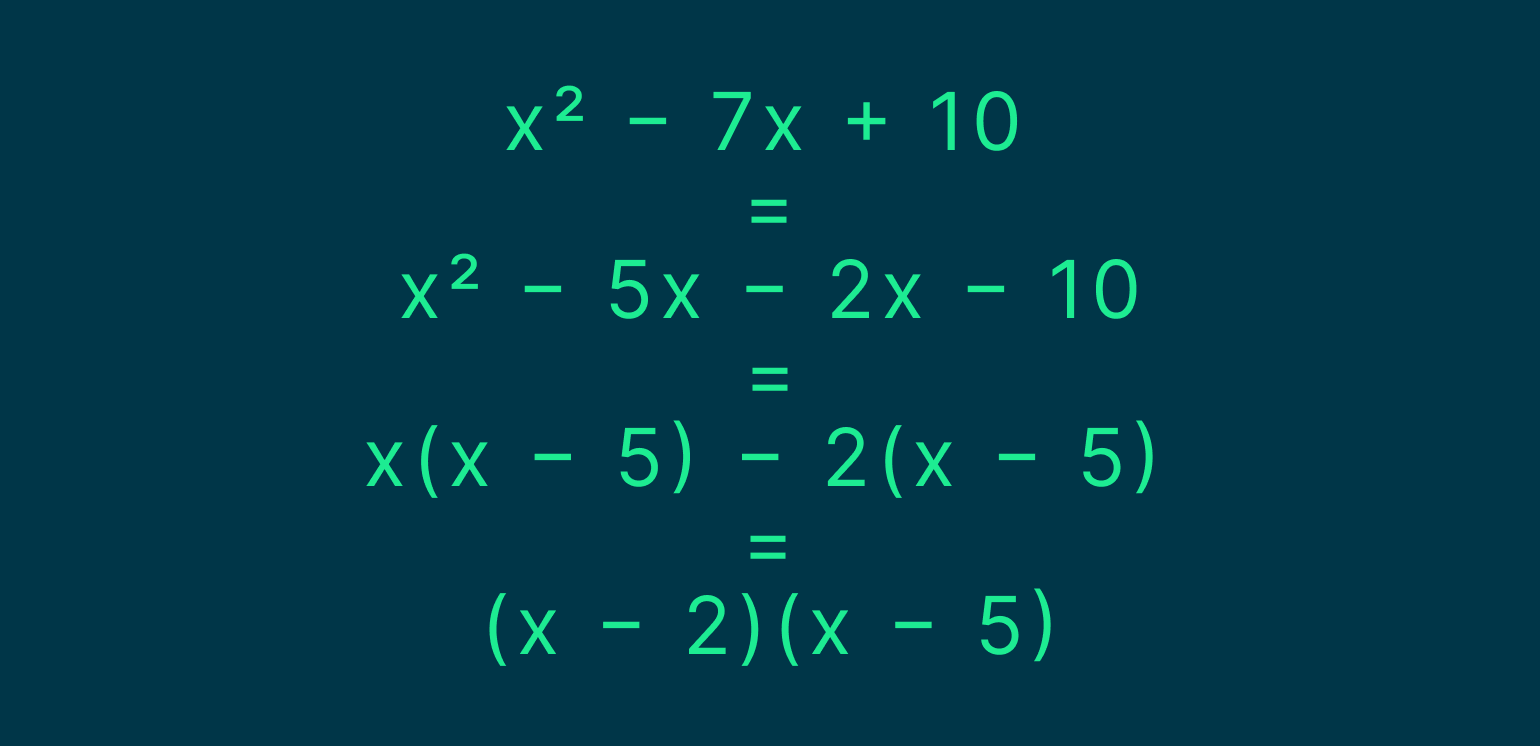
Подставим в функцию числитель и знаменатель:

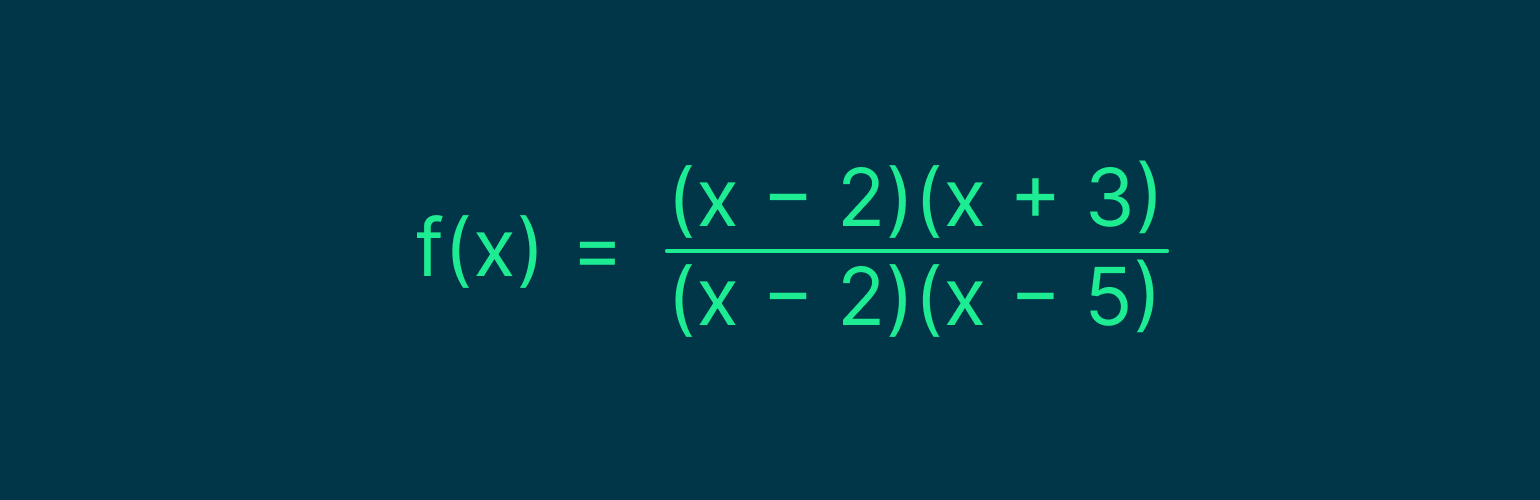
Сократим дробь на (x − 2). В результате получим:

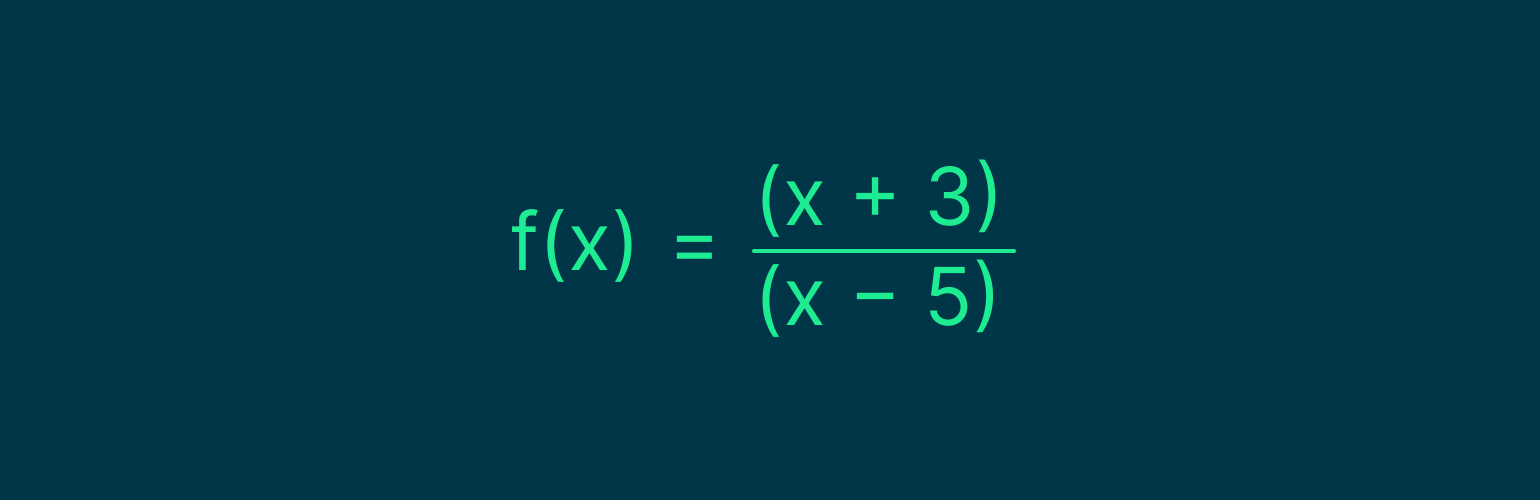
Найдём предел функции при х, стремящемся к 2. Для этого просто подставим в формулу х = 2. Получим:

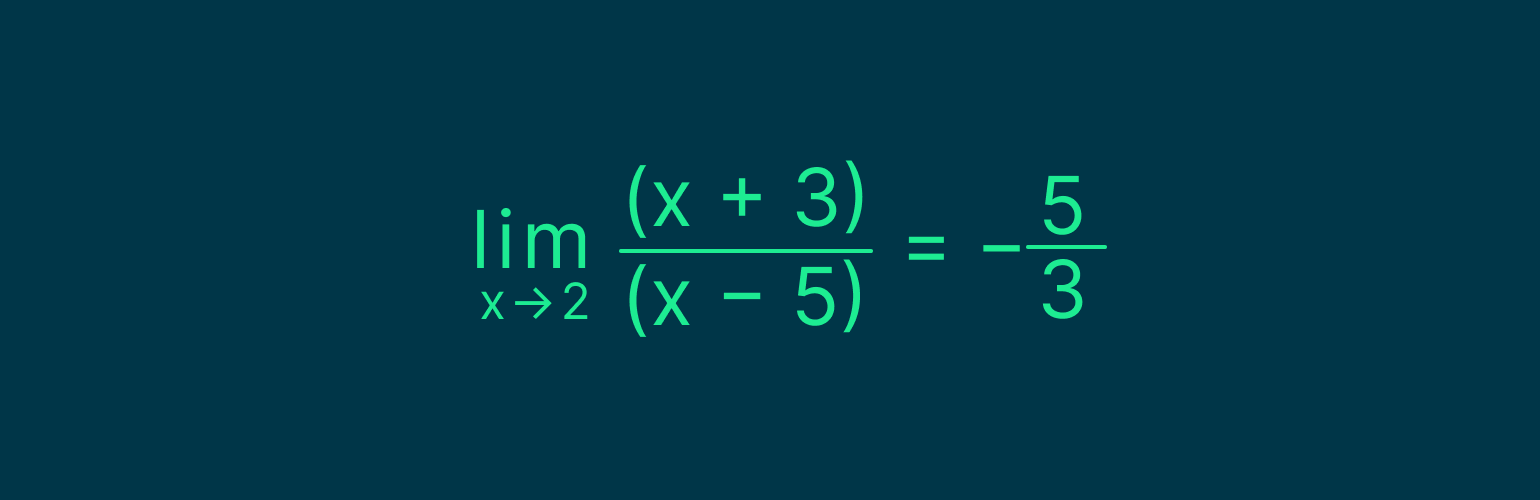
Неопределённость ∞ − ∞

Рассмотрим пример:

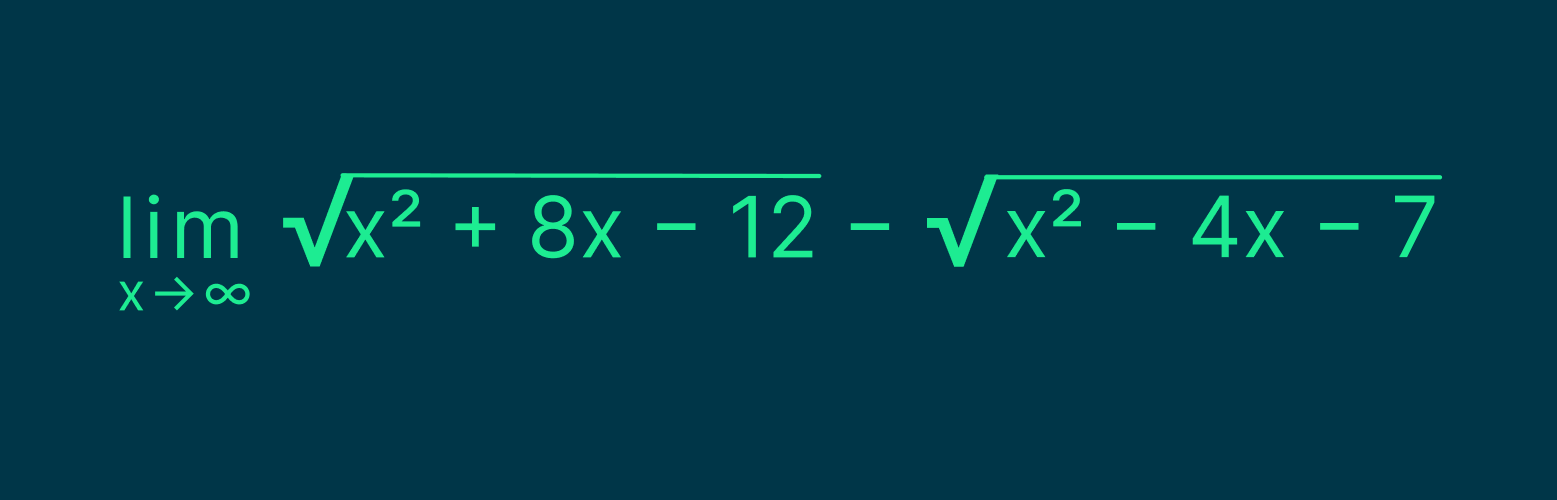
Здесь имеет место неопределённость вида ∞ — ∞, которая может быть равна любому числу.

Избавимся от неё. Для этого умножим и разделим выражение на сопряжённое, чтобы прийти к следующей формуле:

В результате получим:

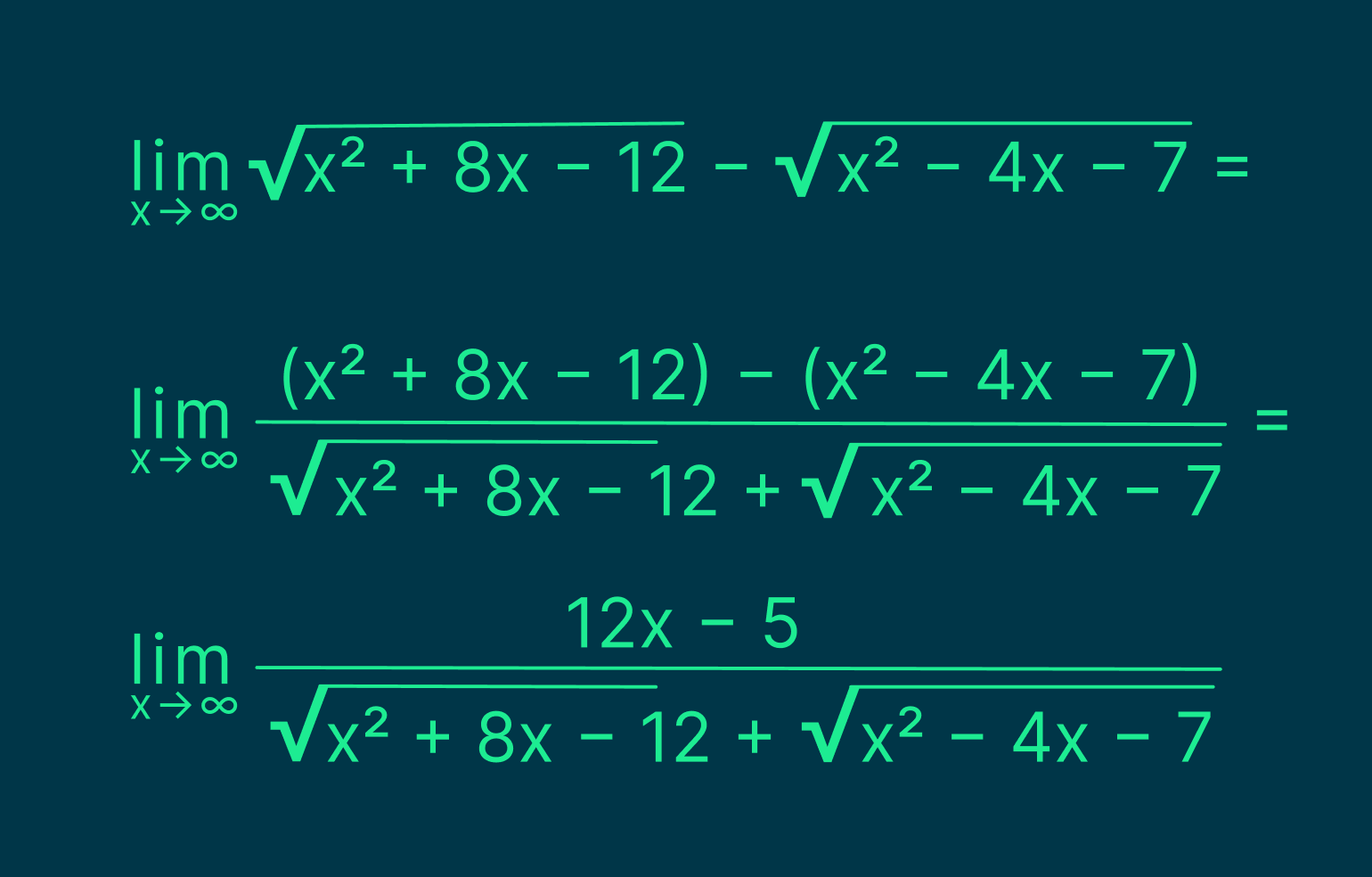
Таким образом мы пришли к неопределённости ∞/∞, которую уже умеем раскрывать.

Разделим числитель и знаменатель на x. Так как дроби с x в знаменателе стремятся к 0 при x, стремящемся к бесконечности, мы получим:

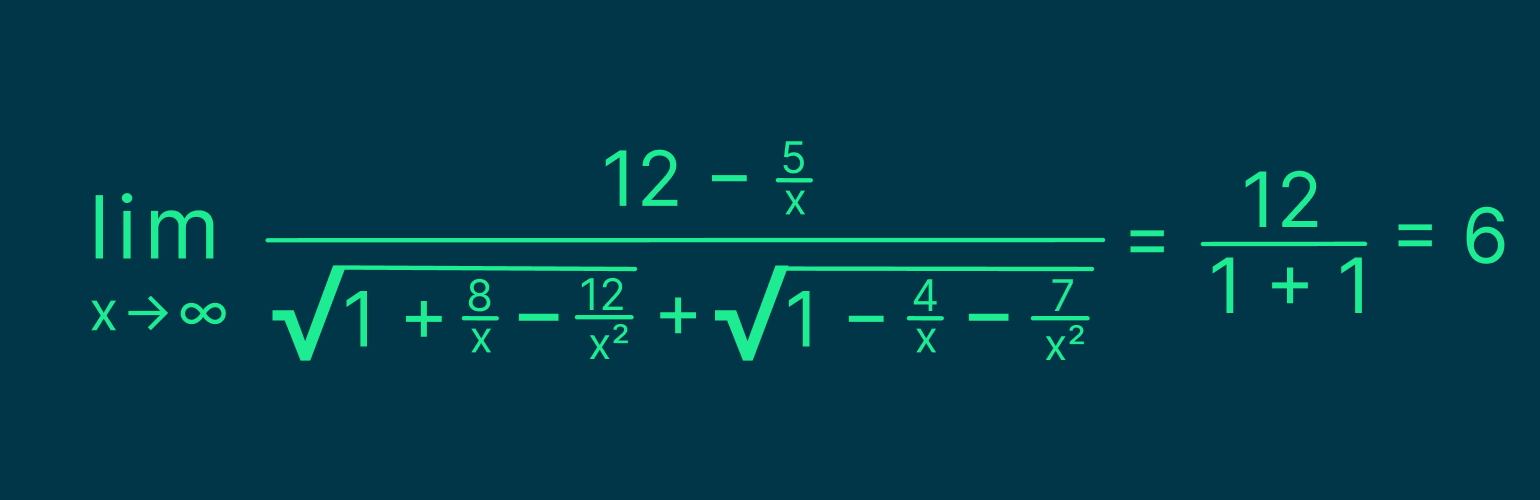
Таблица пределов

При решении задач удобно пользоваться списком пределов — он помогает понять поведение стандартных функций. Для вычисления достаточно подставить числа в формулу.

Что запомнить

Вспомним то, что узнали сегодня:

• Предел функции — это значение, к которому стремится функция, когда её аргумент приближается к определённой точке, то есть к какому-то числу.
• Самый простой способ найти предел функции — подставить в функцию значение, к которому стремится её аргумент.
• Не существует универсального метода нахождения любого предела и раскрытия всех неопределённостей. Выбор способа решения зависит от конкретной задачи. В этом помогут таблицы пределов для стандартных функций.