Пасхальные алгоритмы: как делают механические компьютеры для расчёта православных дат
Почему Христос каждый раз воскресает по-новому и при чём здесь Гаусс и компьютеры, — а также пара слов о российском калькуляторе.


В этом году православные отметили Пасху 24 апреля. В следующем она будет 16 апреля, а в прошлом и вовсе была 2 мая. При этом у католиков Светлое Христово Воскресение прошло на неделю раньше, а иудеи вообще относятся к этой идее, мягко говоря, настороженно и справляют Песах.
Откуда такая путаница? Да и путаница ли это? Или этакий краковяк вприсядку, подчинённый строжайшим математическим алгоритмам? Давайте разбираться.
Исторические предпосылки дат с «плавающей точкой»
Начнём с небольшого исторического экскурса. В первые годы и даже века христианства всё шло ровно.
Счастливые часов не наблюдают. Апостолы так обрадовались воскресению Христа, что забыли зафиксировать точную дату. Причём все сразу — и Матфей, и Лука с Марком, и даже неверующий Фома, который тщательно исследовал все шрамы и следы гвоздей на Чреслах Господних, но постеснялся составить протокол установленной формы: с числом, месяцем, годом и подписями понятых. И пошло-поехало.

Изображение: Public Domain
В каждой избушке — свои погремушки. Не прошло и века, как случился первый раскол. В Малой Азии, если верить Евсевию Кесарийскому, «праздновали Пасху в день, когда народ иудейский отлагал квасный хлеб», а именно в 14-й день нисана — лунного иудейского месяца, приходящегося где-то на март-апрель. Остальные христиане отмечали праздник строго по воскресеньям (что логично), хотя и старались придерживаться той же недели, что и палестинские братья по вере.
Проблема была в том, что иудейский календарь не унифицировали и в каждом городе использовали собственную методику расчёта. Кроме того, 14-й день нисана периодически случался до весеннего равноденствия, что категорически не устраивало многих богословов, считавших, что праздновать надо строго после. В общем, требовалось какое-то решение.
Стандарт — основа качества. Впервые получилось прийти к какому-то согласию на Никейском соборе в 325 году. Там решили отказаться от иудейской практики и праздновать Пасху после полнолуния. Правда, единой методики расчёта так и не разработали — на это потребовалось ещё несколько веков.
Некоторое время существовало два наиболее популярных способа: по александрийским и по римским таблицам. И только в VI веке римский аббат Дионисий Малый объединил их, перевёл в юлианский календарь и составил собственные таблицы. Через двести лет они стали более или менее общеупотребимыми и применялись в Западной Европе вплоть до григорианской календарной реформы.
Новая метла по-новому метёт. В 1582 году Папа Римский Григорий XIII ввёл григорианскую пасхалию, которая используется Римско-католической церковью по сей день.
Что русскому хорошо, то немцу смерть. Через год Григорий XIII предложил перейти на единый стандарт и патриарху Константинопольскому Иеремии II, но получил отказ. На том сердце и успокоилось, и обе методики в практически неизменном виде сохранились до наших дней.
Компьютер в помощь
Как же происходит расчёт? Вы будете смеяться, но уже более двух тысячелетий его ведут с помощью «компьютера». На латыни способ вычисления пасхальных дат так и называется — computus, или computare, от слов com (вместе) и putare (считать, полагать, рассматривать, рассчитывать).
В основу алгоритма положена так называемая лунная епакта, то есть возраст Луны на определённую дату. Да, не забудьте ещё, что лунные годы бывают простые, с двенадцатью месяцами в году, и эмболисмические — с тринадцатью. Дальше всё просто.

Изображение: Public Domain
В александрийской пасхалии, которую использует православная церковь, под епактой понимается возраст Луны 22 марта. Пасхальное полнолуние определяется так:
- Первый год 19-летнего цикла выбирают с епактой на 22 марта, равной 0 (nulla epacta).
- Епакта следующего года = епакта предыдущего года + 11, если предыдущий год был простым, или епакта = епакта предыдущего года –19, если эмболисмическим).
- Если епакта ≤ 15, то следующее полнолуние (22 + 14 − епакта) марта является пасхальным полнолунием.
- Если епакта > 15, то к текущему лунному году нужно добавить полный месяц (30 дней), сделав год эмболисмическим, и пасхальным полнолунием будет (22 + 30 + 14 − епакта) марта = (35 − епакта) апреля.
Что, запутались? А как вы хотели: пасхальный день вычислять — это вам не зарплату в Excel набивать. Компьютер — наука серьёзная, тут думать надо.
Тут и Гаусс подоспел
Возможно, все эти епактические мучения продолжались бы до сих пор — но тут на помощь человечеству пришёл сумрачный гений немецкого математика Карла Гаусса, который предложил гораздо более простой алгоритм. Следите за руками.
Для православной Пасхи:
- Разделить номер года на 19, определить остаток от деления a.
- Разделить номер года на 4, определить остаток от деления b.
- Разделить номер года на 7, определить остаток от деления c.
- Разделить сумму 19a + 15 на 30, определить остаток d.
- Разделить сумму 2b + 4c + 6d + 6 на 7 и определить остаток e.
- Определить сумму f = d + e.
- По старому стилю: если f ≤ 9, Пасха будет 22 + f марта; если f > 9, Пасха будет f − 9 апреля.
- По новому стилю: если f ≤ 26, Пасха будет 4 + f апреля; если f > 26, Пасха будет f − 26 мая.
Посчитаем для 2022 года:
2022 = 106 × 19 + 8; а = 8
2022 = 505 × 4 + 2; b = 2
2022 = 288 × 7 + 6; с = 6
19а + 15 = 167; 167 = 5 × 30 + 17; d = 17
2b + 4c + 6d + 6 = 136; 136 = 19 × 7 + 3; е = 3
f = d + e = 17 + 3 = 20
f < 26, значит, Пасха по новому стилю 4 + f = 24 апреля. Всё сходится — спасибо Карлу Гауссу!
Автоматическая Пасха
Имея на руках такой замечательный алгоритм, грех было не воплотить его в механизированное, а лучше автоматизированное, устройство. Так и получилось.
Первые часы-пасхалии были сконструированы даже до Гаусса. Сделал их итальянский мастер Джованни де Донди; работа заняла 16 лет, с 1348 по 1464 год. Правда, у Астрариума (так назывались часы) был существенный недостаток: табличный указатель под кольцом индикации изготовили под обычный, 365‑дневный, год. В високосные де Донди предлагал останавливать часы на сутки.

Фото: Wikimedia Commons
Позже появлялись более мудрёные конструкции — часовщики трудятся над ними и в наше время. В частности, в этом году мы отмечаем 15-летие со дня установки Comput Orthodoxe — пасхального православного калькулятора, изобретённого россиянином Константином Чайкиным на основе Гауссова алгоритма.
Ход работы изобретатель описывает так:
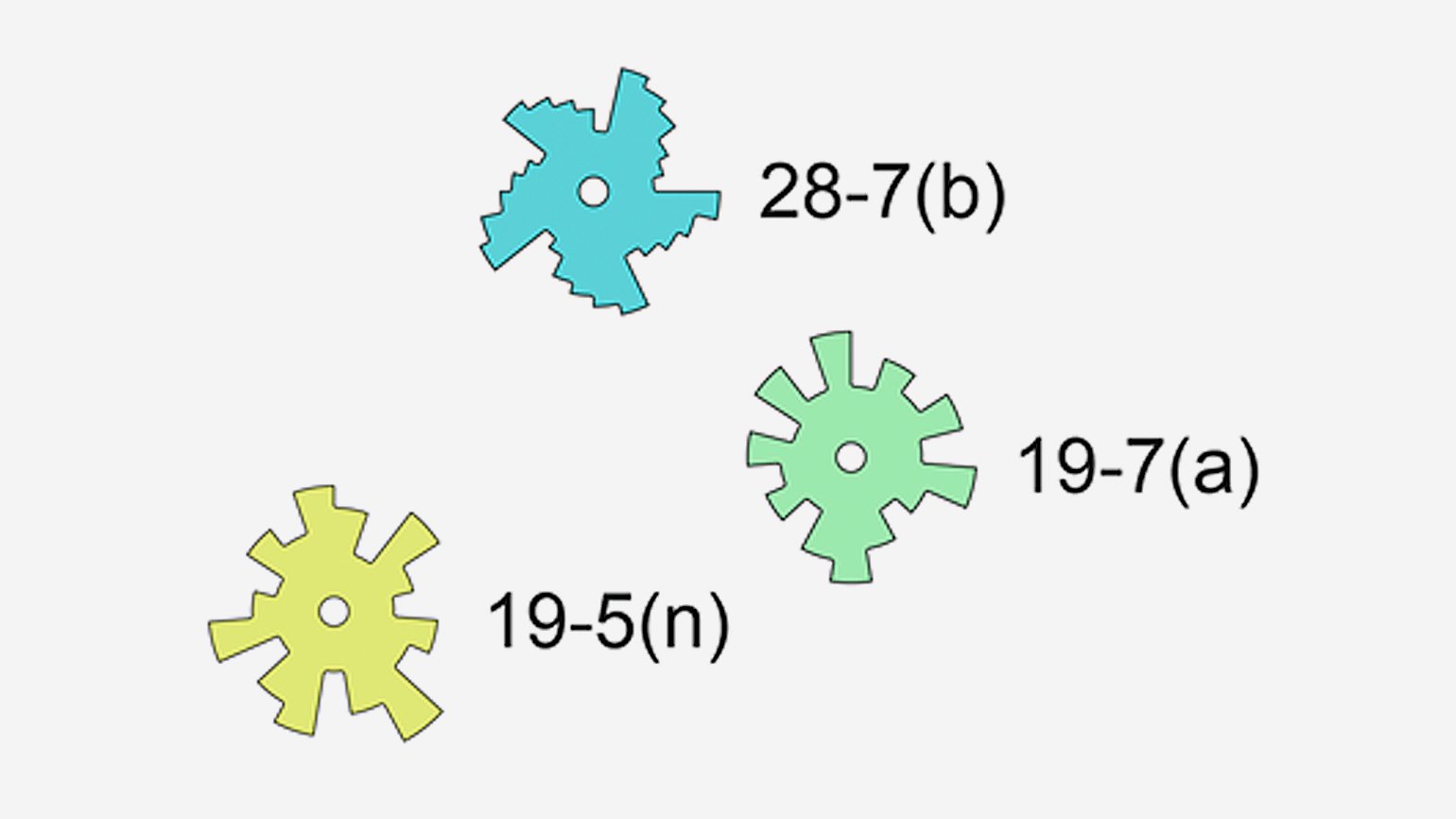
«Суть моего способа заключалась в получении наименьших габаритов программного устройства. Например, не представляется проблемным сделать указатель Пасхи на больших башенных часах, требуется только изготовить колесо, имеющее 532 зуба, разбить его на кулачок с 35 уровнями, и всё готово. Для малогабаритных устройств использование как большого количества зубьев, так и большого количества программных уровней требует экстра-повышенной точности, что с учётом возможностей изготовления непременно вызовет большие погрешности показаний. Таким образом, целью было снизить количество уровней до приемлемого.
Я проанализировал формулы Гаусса, свёл их в таблицы и по их результатам построил три программных диска».
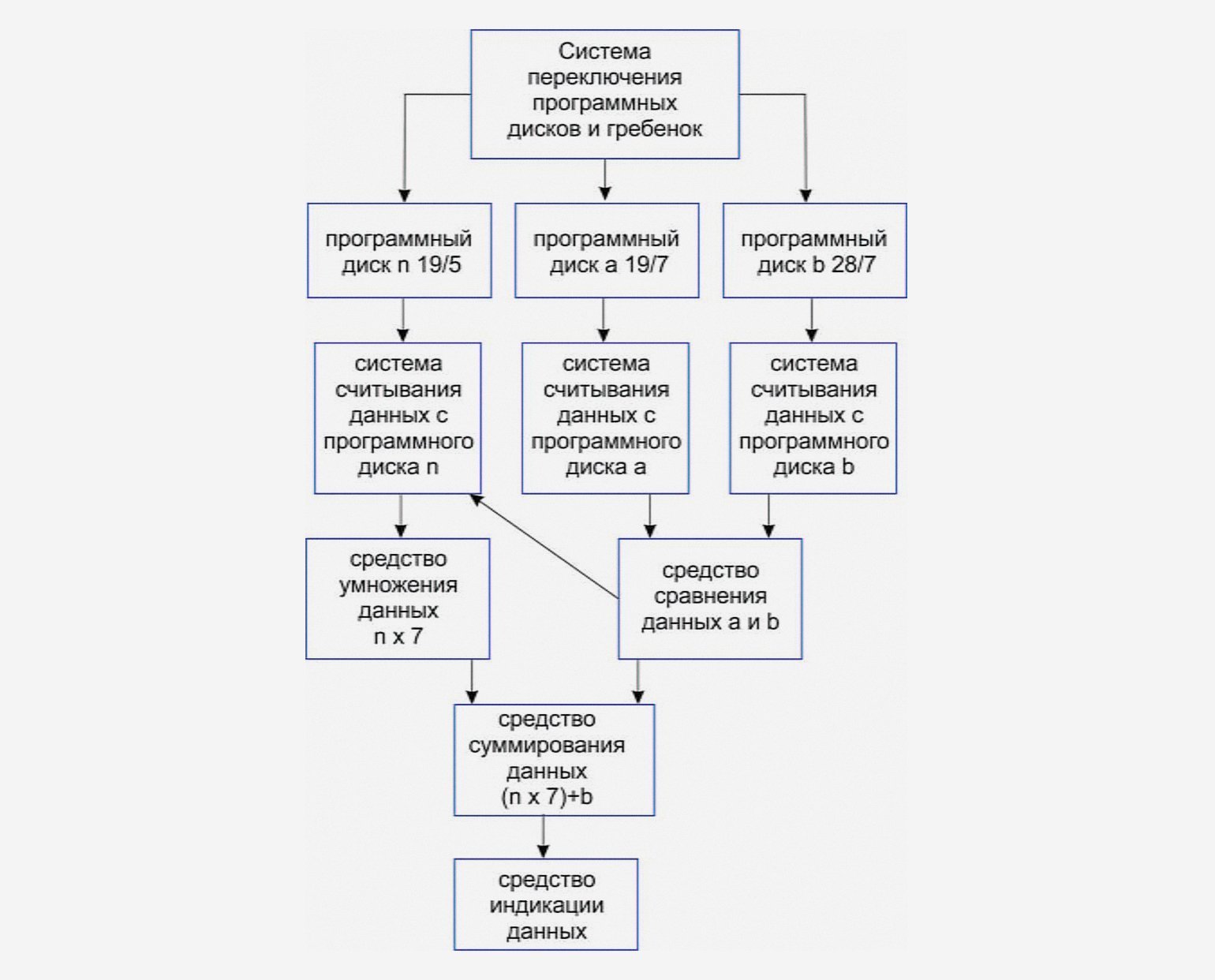
Блок-схема пасхального механизма Чайкина выглядит так:
Так Константин Чайкин собрал механизм, которому по зубам и високосные годы, и объединил в своём изобретении науку и религию.










