Парадокс Монти Холла: одна из самых странных задач в теории вероятностей
Коротко о том, как математика помогает побеждать в телешоу.


Вы только что проиграли машину. Да-да, прямо сейчас — потому что, скорее всего, не знаете, как работает парадокс Монти Холла. В 1990 году из-за него разгорелся один из самых жарких научных споров: после колонки в Parade Magazine Мэрилин вос Савант получила шквал возмущённых писем от профессоров с фразами «Вы позорите науку!».
Сегодня этот парадокс незаметно влияет на A/B-тесты, поиск багов в коде и рекомендательные системы. В этой статье разбираемся, как устроен парадокс Монти Холла и почему иногда выгоднее не стоять на своём упорно.
Содержание
- Что такое парадокс Монти Холла
- Математика за парадоксом: холодный расчёт против интуиции
- Проверяем парадокс с помощью Python
- Почему мы не верим парадоксу Монти Холла
- Парадокс в действии: как IT-специалисты используют стратегию Монти Холла
Что такое парадокс Монти Холла
Парадокс Монти Холла — это знаменитая задача из теории вероятностей, решение которой не так очевидно, как кажется на первый взгляд. Условия задачи основаны на правилах популярной в 1960-х ТВ-игры Let’s Make a Deal, а сам парадокс назван в честь её первого ведущего — Монти Холла.
Представьте, что вы оказались на телевизионном шоу. Перед вами три двери: за одной спрятан автомобиль, а за двумя другими — козы. Ведущий, знающий расположение приза, предлагает вам выбрать любую дверь.
После того как вы делаете выбор, ведущий открывает одну из двух оставшихся дверей — обязательно ту, за которой оказывается коза. Теперь перед вами две закрытые двери, и ведущий предлагает изменить свой первоначальный выбор. На первый взгляд кажется, что шансы победить — 1/2 (или 50 на 50) и менять дверь бессмысленно. Однако математический расчёт говорит обратное.
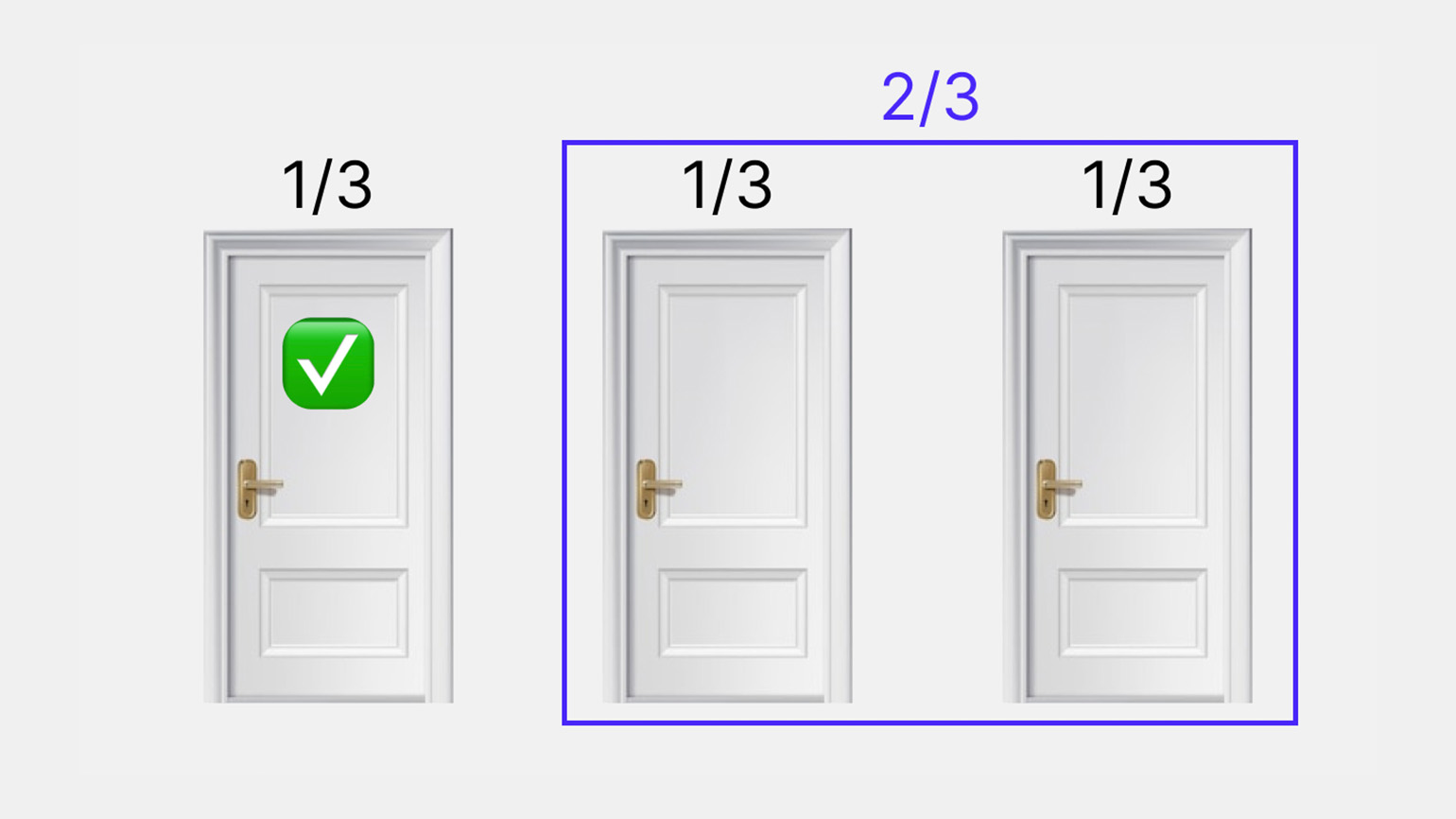
Изображение: Skillbox Media.
Согласно теории вероятностей, если остаться при первоначальном выборе, то вероятность победы составит 1/3. Если выбрать другую дверь — 2/3. Чтобы увеличить шансы на выигрыш, надо соглашаться на предложение ведущего и выбирать другую дверь.
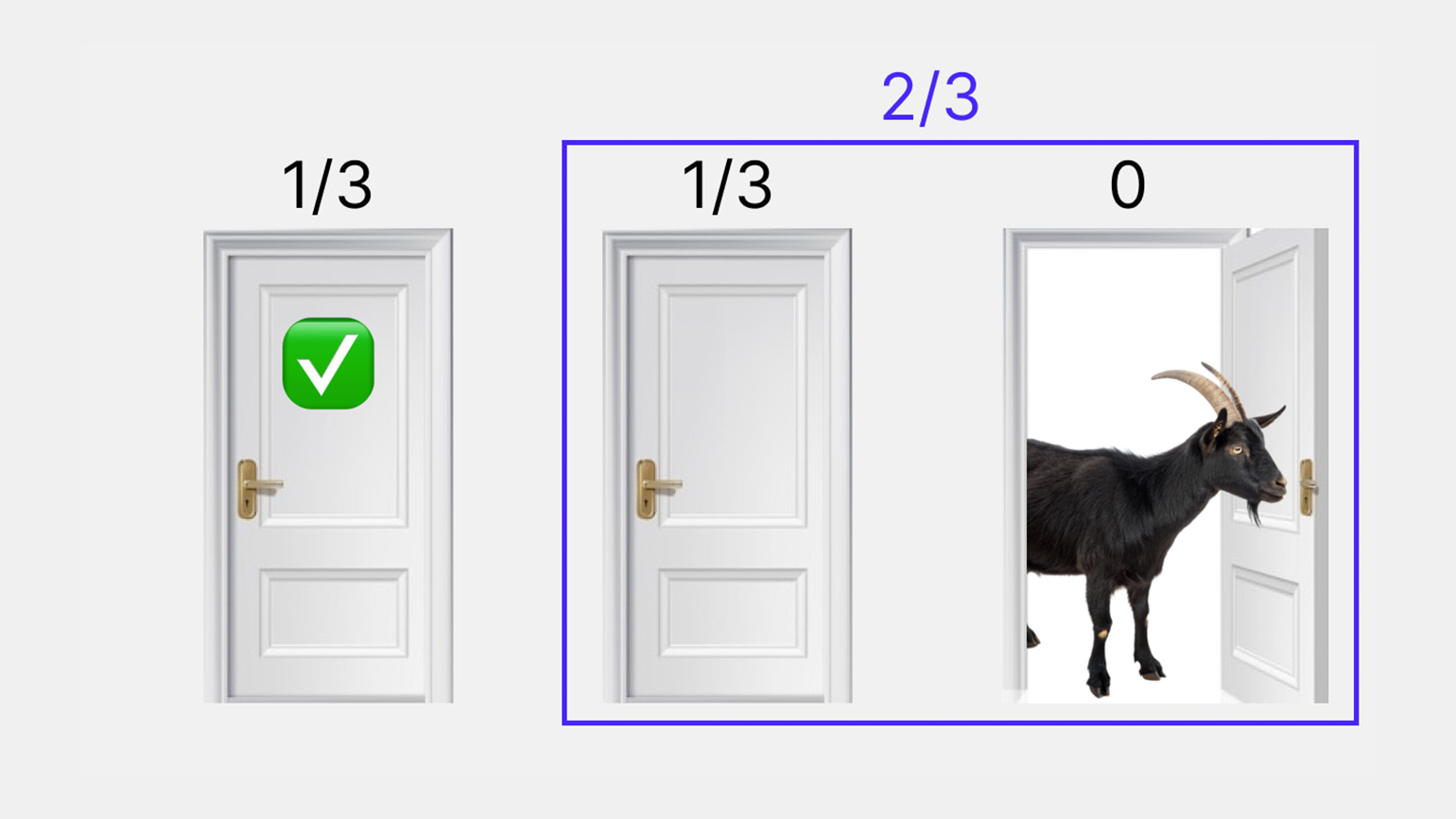
Изображение: Skillbox Meida
Кажется странным, что отказ от первоначального выбора помогает выиграть, — но с математикой спорить сложно. Именно в этом и состоит парадокс Монти Холла: нам кажется, что смена стратегии никак не влияет на вероятность победы, но на деле именно в этом и кроется ключ к ней.
Математика за парадоксом: расчёт против интуиции
Чтобы лучше понять парадокс, представьте: вам нужно поучаствовать в шоу 300 раз. По статистике, в 100 случаях из 300 (примерно 1/3) вы сразу выберете правильную дверь. В оставшихся 200 случаях (2/3) ваш изначальный выбор окажется ошибочным — вы выберете дверь с козой.
Теперь ключевой момент:
- В 200 случаях, когда вы ошиблись, смена выбора приведёт к победе.
- В 100 случаях, когда вы с первого раза угадали дверь, результат будет обратным: смена первоначального выбора приведёт к проигрышу.
- Именно на этом основано математическое преимущество смены стратегии.
Математически это описывается формулой условной вероятности:
P1 = P2 × P3
Где:
- P1 — вероятность выиграть при смене стратегии.
- P2 — вероятность того, что первый выбор был неправильным.
- P3 — условная часть, обозначающая, что ведущий откроет одну из оставшихся дверей, обязательно с козой за ней. Её обозначают единицей.
В итоге получаем:
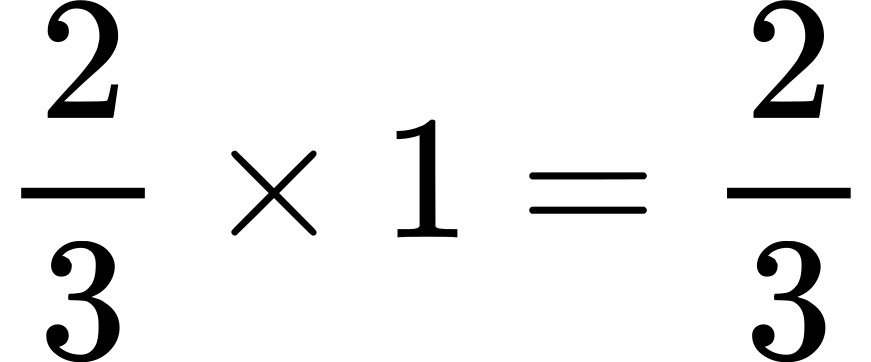
Эта формула показывает, что при смене стратегии шанс выиграть машину с 1/3 увеличивается до 2/3.
Важная оговорка: это справедливо, только если ведущий знает, где находится приз, и специально открывает неправильную дверь. Если по условию задачи он будет открывать случайную дверь, то вероятность победы составит 1/2 и преимущества при смене стратегии не будет.
Проверяем парадокс с помощью программирования
Математические формулы не всем кажутся убедительными, поэтому давайте проверим парадокс Монти Холла с помощью Python. Заставим компьютер 100 тысяч раз поучаствовать в телевизионном шоу и узнаем, поможет ли смена стратегии чаще побеждать. Если вы пока не очень хорошо разбираетесь в Python, то предлагаем сделать паузу и изучить наш гайд.

Читайте также:
В коде симуляции игры Монти Холла мы будем случайным образом размещать приз за одной из трёх дверей, давать компьютеру возможность сделать выбор и сразу же открывать одну неправильную дверь. После этого компьютер будет делать два выбора: со сменой стратегии и без неё.
Вот так выглядит код симуляции на Python:
import random
def monty_hall_simulation(iterations):
stay_wins = 0
switch_wins = 0
for _ in range(iterations):
prize = random.randint(1, 3) # Случайно размещаем приз
choice = random.randint(1, 3) # Игрок выбирает дверь
# Ведущий открывает дверь с козой
opened = next(d for d in [1, 2, 3] if d != prize and d != choice)
# Финал при разных стратегиях
if choice == prize:
stay_wins += 1 # Угадали с первого раза
else:
switch_wins += 1 # Смена выбора привела к победе
print(f"Побед при сохранении выбора: {stay_wins/iterations:.1%}")
print(f"Побед при смене выбора: {switch_wins/iterations:.1%}")
monty_hall_simulation(100_000)Запустим код и получим следующие значения:
Побед при сохранении выбора: 33.4%
Побед при смене выбора: 66.6%Выходит, что смена стратегии на самом деле даёт преимущество — в два раза. Компьютер, в отличие от человека, не сомневается и выигрывает чаще, строго следуя математике.
Почему мы не верим парадоксу Монти Холла
В 1990 году Мэрилин вос Савант, обладательница самого высокого в то время IQ, опубликовала колонку в журнале Parade, где утверждала: в задаче Монти Холла стратегия смены выбора действительно выгоднее.
Реакция читателей была бурной. В редакцию журнала пришло более 10 тысяч гневных писем — от учёных, математиков и преподавателей вузов — с просьбами перестать позорить науку. Вот лишь несколько выдержек:
«Вы очень глубоко заблуждаетесь! Похоже, вам сложно понять основополагающий принцип, поэтому я объясню. После того как ведущий открывает дверь с козой, у вас остаётся шанс угадать правильную дверь 1/2. Не важно, меняете ли вы свой выбор или нет. В этой стране и так полно математической безграмотности, нам не нужен человек с самым высоким IQ, усугубляющий ситуацию. Позор!»
Скотт Смит, доктор наук Университета Флориды
«Я надеюсь, что вы получили много писем на эту тему от учеников старшей школы и студентов колледжей. Сохраните их контакты, возможно, они смогут помочь вам с выпуском следующих колонок».
Роберт Смит, доктор наук Университета Джорджии
«Вы ошиблись в ответе на вопрос телевикторины. Я надеюсь, ваша ошибка поможет привлечь внимание общества к национальному кризису математического образования. Если вы признаете свою ошибку, то это поможет найти выход из сложившейся ситуации. Сколько разъярённых математиков заставит вас поменять точку зрения?»
Рэй Бобо, доктор наук Университета Джорджтауна
Почему было столько негодования?
Дело в том, что Мэрилин не обозначила правила поведения ведущего: специально он открывает неправильную дверь или действует случайно. А это критично:
- Если ведущий знает, где приз, и намеренно открывает неправильную дверь, — смена выбора действительно увеличивает шансы на победу до 2/3.
- Если же он открывает двери наугад — вероятность выигрыша при любом действии становится ½.
Следующие три колонки Мэрилин посвятила детальному разбору задачи Монти Холла и чётко оговорила все условия. Несмотря на это, некоторые читатели всё равно были не согласны с её решением. Их можно понять: парадокс бросает вызов самой природе человеческого мышления.
Наш мозг — продукт миллионов лет эволюции. Он создан для быстрых решений: «Беги от саблезубого тигра», «Не ешь эти ягоды». Но он совершенно не приспособлен для ситуаций, в которых кто-то сознательно манипулирует информацией. Когда ведущий открывает дверь, мы ошибочно воспринимаем это как случайное событие, а не как часть тщательно продуманного сценария.
В 1991 году профессор математики Стэнфордского университета Перси Диаконис отметил, что мозг очень плохо решает задачи по теории вероятностей. Именно поэтому парадокс Монти Холла нам кажется странным.
Парадокс в действии: как IT‑специалисты используют стратегию Монти Холла
Рассмотрим, как парадокс Монти Холла используют на практике:
- A/B-тестирование. Когда вы тестируете три варианта дизайна и один явно проваливается, перераспределение трафика между оставшимися двумя — это буквально «смена двери». Статистика показывает: такие переключения дают в среднем на 22% более точные результаты.
- Оптимизация запросов в базах данных. Представьте, что SQL-запрос можно выполнить тремя способами. После анализа плана выполнения смена стратегии часто ускоряет обработку в 1,5–2 раза.
- Поиск багов. Разработчики часто используют метод трёх гипотез, когда ищут ошибке в коде. Допустим, ваш проект работает очень медленно. В этом случае лучше всего выдвинуть три причины и начать проверять их по очереди. При этом вы, скорее всего, отдаёте предпочтение одной из гипотез. Когда первая теория окажется ошибочной, просто смените своего претендента, чтобы повысить вероятность.
- Рекомендательные алгоритмы. Маркетологи в IT-компаниях ловко используют парадокс Монти Холла для рекомендаций. Например, в 2017 году аналитики Netflix заметили закономерность. Если предложить пользователю выбрать один фильм из трёх, а затем посоветовать переключиться на альтернативный вариант, то показатели досматриваемости будут в 1,8 раза выше.
Что в итоге
Парадокс Монти Холла перестал быть просто занимательной задачей из теории вероятностей. Как мы убедились, его принципы находят неожиданное применение в современных IT-системах.
Вот что важно помнить:
- Интуиция часто даёт сбой — даже опытные специалисты склонны недооценивать влияние дополнительной информации на вероятности.
- Стратегия «переключения» работает: будь то выбор алгоритма, поиск уязвимостей или A/B-тестирование — смена начальной гипотезы часто приводит к успеху.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!








