Основы систем счисления: от счётных палочек до машинного кода
Путешествие по математической летописи человечества.


В работе специалистов по кибербезопасности часто встречаются разные системы счисления. Например, при анализе логов они сталкиваются с IP-адресами в различных форматах. Тот же IP-адрес 192.168.1.1 можно встретить в двоичном виде как 11000000.10101000.00000001.00000001, а в шестнадцатеричном — как C0.A8.01.01. Понимание этих форматов помогает анализировать сетевой трафик и находить потенциальные угрозы.
Но что такое система счисления? В этой статье мы заглянем в историю их развития и разберёмся, как переводить числа между разными системами.
Содержание
- Единичная система счисления
- Древнеегипетская десятичная система
- Римская система счисления
- Греческая и славянская системы счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Десятичная система счисления
- Шестнадцатеричная система счисления
Основные системы счисления
Система счисления — это математический язык, в котором вы можете использовать символы для записи чисел по определённым правилам.
На протяжении истории человечества люди разработали множество способов записи чисел, но сегодня принято выделять два основных типа:
- Непозиционные системы — древнейшие системы счисления, в которых значение символа остаётся неизменным вне зависимости от его места в числе. Например, в римской системе символ X всегда обозначает 10, независимо от того, стоит ли он в начале (XVI = 16) или в конце (LX = 60).
- Позиционные системы — системы счисления, где значение цифры определяется её положением в числе. Например, в числе 333 у каждой тройки разное значение: первая означает 300, вторая — 30, а третья — 3.
Каждая система счисления имеет свою область применения. Позиционные системы подходят для вычислений — сложить числа 23 и 45 проще, чем XXIII и XLV в римской системе. Непозиционные системы используются реже — например, в нумерации глав книг (I, II, III) или обозначении веков (XX век).
В следующих разделах мы рассмотрим обе системы счисления. Начнём с непозиционных систем и выясним, почему они уступили место позиционным. После изучим позиционные системы — познакомимся с их видами и научимся конвертировать числа между разными форматами.
Непозиционные системы счисления
Непозиционные системы счисления сформировались естественным образом с развитием человечества. Вот основные предпосылки их появления:
- Древним цивилизациям требовался надёжный способ учёта товаров, землемерия, строительства и астрономических наблюдений.
- Развитие письменности позволило записывать числовые значения.
- Использование отдельных символов для записи чисел оказалось интуитивно понятным способом счёта.
К наиболее известным непозиционным системам счисления относятся единичная, древнеегипетская, римская, греческая и славянская. Далее мы рассмотрим особенности и историческую значимость каждой из них.
Единичная система счисления
Единичная система счисления — это простейший способ записи чисел, в котором количество обозначается повторением одного и того же символа столько раз, сколько единиц содержится в числе. Она возникла естественным путём из процесса подсчёта предметов в период, когда более сложные математические концепции ещё не существовали.
Люди изображали предметы счёта в виде разных символов: палочек, камешков, узелков — всего, что было под рукой. Применялась система в разных сферах: от древних способов подсчёта дней с помощью зарубок на дереве или камне до современного использования в простых играх для ведения счёта. Записать число в этой системе очень просто — например, число 5 записывается как пять палочек (|||||), а число 3 — как три палочки (|||).
Единичная система хорошо подходила для простейших арифметических действий — сложения и вычитания. Однако при работе с большими числами возникал риск ошибок как в записи, так и в подсчёте. Например, запись числа 100 потребовала бы изображения ста отдельных палочек. Именно поэтому в ходе развития цивилизации люди перешли к группировке символов, что привело к появлению более эффективных систем счисления.
Изображение: Benjamin D. Esham / Wikimedia Commons
Древнеегипетская десятичная система
Древнеегипетская десятичная система — это система счисления с основанием 10. Она была неотъемлемой частью жизни древних египтян и применялась в торговле, строительстве пирамид, земледелии и астрономии. Для записи чисел использовались особые символы: палочка (1), арка (10), моток верёвки (100), водяная лилия (1000), согнутый палец (10 000), лягушка или головастик (100 000) и человек с поднятыми руками (1 000 000).
Древние египтяне не придавали особого значения направлению записи чисел — они могли писать их слева направо, справа налево или сверху вниз. Учёные обнаружили у них особый знак, который выполнял функции нуля — изображался в виде сердца с трахеей. В бухгалтерских папирусах этот знак указывал на полный расход средств, а в чертежах обозначал уровень земли.
Египтяне также использовали дроби в своих вычислениях. Они записывали их похожим на современный способом — размещали над числом специальный иероглиф в форме рта, который обозначал часть целого.
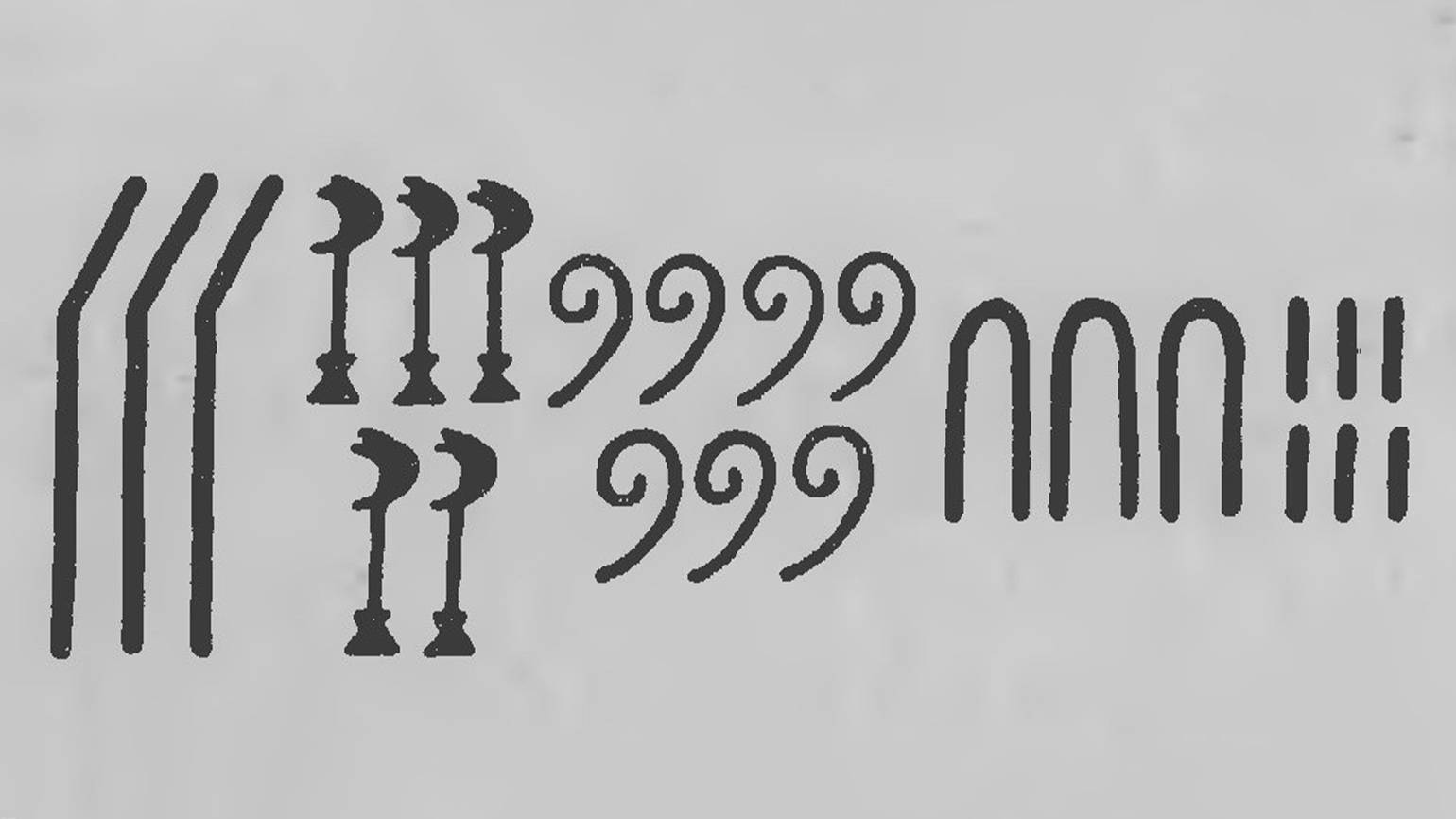
Изображение: Public Domain / Wikimedia Commons
Римская система счисления
Римская система счисления — это система записи чисел с помощью букв латинского алфавита. В её основе лежит принцип сложения и вычитания значений символов, где каждая буква обозначает определённое число. Основные символы: I (1), V (5), X (10), L (50), C (100), D (500) и M (1000).
Каждое число — это последовательность символов, записанная по определённым правилам. Значение такого числа складывается из значений всех его символов. Например, число 32 записывается как XXXII (30 + 2 = 32).
Если слева от большего символа стоит меньший, то его значение вычитается из большего. Например, число 48 записывается как XLVIII: из 50 (L) вычитается 10 (X), после чего прибавляется 5 (V) и 3 (III). Важно отметить, что слева от большего символа может стоять только один меньший символ — запись XXL недопустима и не может обозначать число 30.
В современном мире римские цифры используются для обозначения веков, глав в книгах, часов на циферблатах, а также порядковых номеров правителей и мероприятий — XXI век, глава IV, Карл V, том III, Пётр I.

Фото: Alex1011 / Wikimedia Commons
Греческая и славянская системы счисления
Греческая и славянская системы счисления — алфавитные системы записи чисел, где числовые значения передаются буквами. Греческая система использовала греческий алфавит, а славянская — кириллицу. Обе системы применялись в религиозных текстах, летописях и деловых документах.
В греческой системе буква «альфа» означала 1, «бета» — 2, «йота» — 10, а в славянской системе буква «аз» означала 1, «веди» — 2, «и десятеричное» — 10. Для обозначения тысяч применялся специальный знак, а числовое значение буквы выделялось титлом (надстрочным знаком).
Числа записывались слева направо по убыванию — от большего к меньшему. Особый случай представляли числа от 11 до 19: в них единицы записывались перед десятками. Этот принцип можно увидеть и в современном языке при сравнении чисел разного порядка. Например, когда мы говорим «шестьдесят один», сначала называем десятки («шестьдесят»), потом единицы («один»). А в числе «шестнадцать» порядок обратный — сначала называем единицы («шесть»), затем числительное «надцать», обозначающее прибавление к десяти.
Главными достоинствами этих систем были их органичное слияние с письменностью и доступность для образованных людей того времени.

Изображение: Tcr25 / Wikimedia Commons
Позиционные системы счисления
Несмотря на свою историческую значимость, непозиционные системы счисления имеют существенные недостатки, которые привели к их замене позиционными системами в большинстве сфер применения:
- Сложность арифметических действий — например, в римской системе умножение и деление требуют сложных поэтапных вычислений.
- Отсутствие универсальности — каждая система требует уникального набора символов, что затрудняет международное взаимодействие.
- Громоздкость — большие числа требуют чрезмерно много символов.
Позиционные системы, напротив, очень удобны: в них не возникает разночтений при записи чисел, а количество разрядов не имеет ограничений — можно записать любое число, каким бы большим оно ни было.
Все позиционные системы делятся на две основные категории: однородные и неоднородные (смешанные). Рассмотрим особенности каждой из них.
Однородные позиционные системы счисления
Однородная система счисления — это позиционная система, в которой применяется единое основание для всех разрядов числа. Значение числа в такой системе определяется как цифрами, так и их позицией. Каждая позиция в числе имеет свой «вес» — это основание системы, возведённое в степень, равную номеру позиции. Чтобы получить значение числа, нужно умножить каждую цифру на «вес» её позиции и сложить результаты.
Наиболее распространенными позиционными системами счисления являются двоичная, восьмеричная, десятичная и шестнадцатеричная.
Двоичная система счисления
Это способ представления чисел с помощью всего двух символов: 0 и 1. В этой системе каждая позиция числа представляет степень двойки, начиная с нулевой степени справа налево. Например, число 42 в двоичной системе записывается как 101010, где каждая позиция соответствует степени двойки (32 + 0 + 8 + 0 + 2 + 0 = 42).
Данная система получила широкое применение в вычислительной технике:
- Простота реализации — электронные схемы эффективно работают с двумя состояниями: наличием либо отсутствием электрического тока.
- Надёжность — использование всего двух состояний значительно уменьшает вероятность ошибок при передаче и обработке сигналов.
- Экономичность — обработка двоичных данных требует минимума компонентов: транзисторов, резисторов, конденсаторов и микросхем.
Восьмеричная система счисления
Это способ записи чисел с использованием восьми цифр (от 0 до 7). В этой системе значение каждого разряда определяется умножением на соответствующую степень числа 8. Например, 147₈ в восьмеричной системе можно разложить так: 1 × 8² + 4 × 8¹ + 7 × 8⁰ = 64 + 32 + 7 = 103 в десятичной системе.
Восьмеричная система была создана для упрощения работы с двоичными числами благодаря более компактной записи. Это было важно на раннем этапе развития компьютерной техники, когда память была ограничена. Так, восьмеричное число 7₈ соответствует двоичному 111₂, а 6₈ — числу 110₂.
В современных компьютерных системах восьмеричная система счисления применяется, но уступает место шестнадцатеричной. Шестнадцатеричная система эффективнее для записи байтов — один байт данных можно представить всего двумя шестнадцатеричными знаками. Это делает её особенно удобной для низкоуровневого программирования и отладки.

Читайте также:
Десятичная система счисления
Это способ записи чисел с помощью десяти цифр (от 0 до 9), в котором каждая позиция числа представляет определённую степень десятки. Число 567 можно разложить 5 × 10² + 6 × 10¹ + 7 × 10⁰, или записать проще — 500 + 60 + 7.
Появление десятичной системы связано с естественным фактором — десятью пальцами рук человека, которые издревле служили для счёта. Система широко распространилась в Индии в V–VI веках нашей эры, откуда через арабских математиков пришла в Европу. Арабские цифры заменили римские, что значительно упростило сложные математические вычисления и заложило фундамент современной десятичной системы.
В нашей повседневной жизни десятичная система применяется повсеместно — в торговле, банковском деле, науке и технике. В денежных расчётах мы используем рубли и копейки (1 рубль = 100 копеек), а при измерении температуры — градусы Цельсия с десятыми долями (например, 36,6 °C). А ещё для записи дробных чисел у нас есть десятичная точка или запятая, которые позволяют выражать числа с любой необходимой точностью.

Фото: Research and Conservation Center for Excavated Texts / Tsinghua University / Wikimedia Commons
Шестнадцатеричная система счисления
Это способ записи чисел с использованием 16 символов. Она включает цифры от 0 до 9 и шесть букв латинского алфавита (A, B, C, D, E, F), которые обозначают числа от 10 до 15. Эта система была создана специально для работы с компьютерными данными, так как позволяет компактно представлять двоичные числа.
Сегодня шестнадцатеричная система применяется в различных областях:
- В веб-разработке — для обозначения цветов в CSS. Например, код #FF5733 обозначает оранжевый цвет.
- В криптографии — для представления хеш-значений. Так, код 8A4B2C1D служит для проверки целостности данных.
- В сетевых технологиях — для записи IP-адресов. Например, адрес 2001:0db8:85a3 используется в протоколе IPv6.
- В игровой индустрии — для отладки программ и тестирования игр, например, код 0xDEADBEEF указывает на сбой программного обеспечения.
- В системном программировании — для обозначения ошибок и состояний системы, где код 0×0000FFFF указывает на тип сбоя.

Читайте также:
Смешанные системы счисления
Неоднородные, или смешанные, системы счисления — это особый тип позиционных систем, где каждый разряд может иметь своё основание. В таких системах числа записываются с разными базами, которые зависят от позиции цифры. Ключевая особенность состоит в том, что вес каждой цифры вычисляется как произведение оснований всех младших разрядов.
Рассмотрим смешанную систему, где каждый разряд имеет своё собственное основание: первый разряд — 2, второй — 3, третий — 4 (записывается как [2, 3, 4]). В такой системе число 123 раскладывается следующим образом:
- Первая цифра (1) умножается на произведение всех младших оснований:
1 × (3 × 4) = 12. - Вторая цифра (2) умножается на основание младшего разряда: 2 × 4 = 8.
- Третья цифра (3) умножается на 1: 3 × 1 = 3.
- Сумма всех значений (12 + 8 + 3) даёт число 23 в десятичной системе.
Вавилонская шестидесятеричная система считается одной из древнейших смешанных систем. В ней используются символы от 0 до 59, а каждый разряд представляет собой степень числа 60. Значение символа зависит от его позиции, при этом каждый следующий разряд увеличивает число в 60 раз.
Вавилонская система использовала два основных символа: вертикальный клин для обозначения единиц и горизонтальный клин для десятков. Числа записывались справа налево, а новый разряд начинался после определённой комбинации этих символов. Вертикальный клин имел двойное значение — обозначал как единицу, так и число 60 с его степенями, откуда и пошло название «шестидесятеричная система». Позиционный характер системы проявлялся в том, что при записи чисел больше 60 значение символа (1 или 60) определялось его положением в числе.
С развитием торговли и астрономии вавилоняне начали записывать не только целые числа, но и дроби. Для этого они усовершенствовали систему и добавили дополнительные разряды после целой части числа. Так появилась смешанная форма записи: целая часть записывалась в шестидесятеричной системе, а каждый разряд дробной части представлял деление на 60.
Вавилонская система оказалась настолько эффективной, что стала основой множества современных измерительных приборов — от наручных часов до высокоточных навигационных систем GPS. Рассмотрим современные часы с точным временем. Например, 10:45:30. В этом формате каждый компонент использует свою систему счисления: часы отображаются в 12- или 24-часовом формате, а минуты и секунды — в 60-ричной системе (от 0 до 59).

Изображение: Josell7 / Wikimedia Commons
Перевод из одной системы в другую
Разработчики приходится регулярно сталкиваться с разными системами счисления. Вот несколько ситуаций, где нужно выполнять преобразования:
- При работе с битовыми операциями и масками для оптимизации кода и улучшения производительности программ. Например, число 1111 в двоичной системе (0b1111) соответствует F в шестнадцатеричной (0xF).
- При анализе и отладке программ для эффективного управления памятью и поиска ошибок. Пример: адрес в памяти 4095 в десятичной системе соответствует 0xFFF в шестнадцатеричной.
- При настройке сетевого оборудования для конфигурации и диагностики устройств. Например, IP-адрес 127.0.0.1 в десятичной записи соответствует 7F.00.00.01 в шестнадцатеричной.
- В криптографии и защите информации для обработки и верификации зашифрованных данных. К примеру, ключ шифрования может быть представлен как в двоичном, так и в шестнадцатеричном виде.
- При работе с цветовыми кодами в веб-разработке и графическом дизайне. Так, чистый синий цвет RGB (0, 0, 255) в десятичной системе записывается как #0000FF в шестнадцатеричной.
Для перевода чисел между система есть три основных метода: деление с остатком, умножение с накоплением и использование таблиц соответствия.
Метод деления с остатком работает следующим образом: исходное число делим на основание новой системы счисления и записываем остаток от деления. Повторяем эти действия с полученным частным до тех пор, пока оно не станет равным нулю. Затем записываем все остатки в обратном порядке — это и будет результат. Переведём число 83₁₀ в двоичную систему:
- 83 ÷ 2 = 41 (остаток 1);
- 41 ÷ 2 = 20 (остаток 1);
- 20 ÷ 2 = 10 (остаток 0);
- 10 ÷ 2 = 5 (остаток 0);
- 5 ÷ 2 = 2 (остаток 1);
- 2 ÷ 2 = 1 (остаток 0);
- 1 ÷ 2 = 0 (остаток 1);
- Результат: 83₁₀ = 1010011₂.
Метод умножения с накоплением — это способ перевода чисел в систему с большим основанием. Например, из двоичной в десятичную. Метод состоит из двух шагов. Сначала нам нужно взять каждую цифру исходного числа и умножить её на основание системы в степени её позиции (позиции считаем справа налево от нуля). После этого просто складываем все полученные результаты. Переведём 101₂ в десятичную систему:
Метод умножения с накоплением — это способ перевода чисел в систему с большим основанием. Например, из двоичной в десятичную. Метод выполняется в два шага: сначала мы каждую цифру исходного числа умножаем на основание системы в степени её позиции (позиции считаются справа налево, начиная с нуля), а затем складываем полученные результаты.
Переведём 101₂ в десятичную систему:
- Первая цифра справа (1): 1 × 2⁰ = 1.
- Средняя цифра (0): 0 × 2¹ = 0.
- Последняя цифра (1): 1 × 2² = 4.
- Складываем: 4 + 0 + 1 = 5₁₀.
Таблицы соответствия — самый простой метод перевода чисел. Он основан на готовых таблицах, которые показывают соответствие цифр между разными системами счисления. Вот несколько полезных ресурсов:
- RapidTables — универсальный онлайн-конвертер для всех основных систем счисления.
- BaseCalc — сервис для перевода чисел между системами счисления с основаниями от 2 до 36.
- Online Binary-Decimal Converter — инструмент для быстрого перевода между двоичными и шестнадцатеричными числами.
- Calculator.net — калькулятор с поддержкой шестнадцатеричных, двоичных, десятичных и восьмеричных вычислений.
- Math Is Fun — полезный образовательный ресурс с подробными объяснениями процесса конвертации чисел.
- WolframAlpha — продвинутый математический ресурс, который не только конвертирует числа, но и показывает пошаговое решение.
В дополнение к описанным методам можно использовать возможности современных языков программирования, так как многие из них имеют встроенные функции для конвертации между системами счисления.
Например, вот некоторые методы языка JavaScript:
// Пример перевода десятичного числа в двоичную систему
let dec = 42;
console.log(dec.toString(2)); // Результат: 101010
// Перевод двоичного числа в десятичную систему
let bin = "1100";
console.log(parseInt(bin, 2)); // Результат: 12
// Перевод из шестнадцатеричной системы в двоичную
let hex = "2F";
console.log(parseInt(hex, 16).toString(2)); // Результат: 101111
// Перевод из восьмеричной системы в двоичную
let oct = "52";
console.log(parseInt(oct, 8).toString(2)); // Результат: 101010Информацию по работе с системами счисления можно найти в официальной документации. Подробные руководства доступны для Python, JavaScript, Java, C++, Ruby, PHP, Go и других языков программирования.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!






