Код

11 май 2022
0

Майк Паунд: что такое регистры сдвига с обратной связью и для чего они нужны

Доктор Майк Паунд рассказывает, как с помощью регистров LFSR генерируют псевдослучайные числа и как их используют для защиты информации.

Фото: Университет Ноттингема

Марина Демидова

Программист, консультант, специалист по документированию. Легко и доступно рассказывает о сложных вещах в программировании и дизайне.

Майкл П. Паунд

Научный сотрудник Ноттингемского университета. Известен своими работами в области анализа биоизображений, компьютерного зрения, распознавания изображений и компьютерной безопасности.

Регистры сдвига с линейной обратной связью, или LFSR (linear feedback shift register), широко применяются в криптографии, в статистике и имитационном моделировании.

Что мне в них действительно нравится — они невероятно просты по структуре и в то же время могут выдавать невероятно сложные результаты. Кроме того, их легко кодировать.

Чтобы понять, о чём речь, вспомним, что регистр — это набор связанных между собой битов, который может хранить, записывать, считывать двоичные данные. А в регистрах сдвига с линейной обратной связью (LFSR) дополнительно установлены некоторые правила того, как перемещать и рассчитывать значения этих битов.

Это пересказ лекции Майкла с канала Computerphile.

Регистры LFSR используются для генерации псевдослучайных чисел, отличающихся от случайных тем, что каждое последующее число рассчитывается по определённой формуле в зависимости от предыдущих чисел.

Последовательность псевдослучайных чисел полностью определяется формулой и первоначально заданным числом. В какой-то момент она зацикливается — например, сначала в ней будет 4095 разных чисел, а с 4096-го числа она начнёт повторяться. Во многих приложениях такой последовательности вполне достаточно.

Регистры LFSR работают так:

Содержимое регистра сдвигается на один бит вправо.
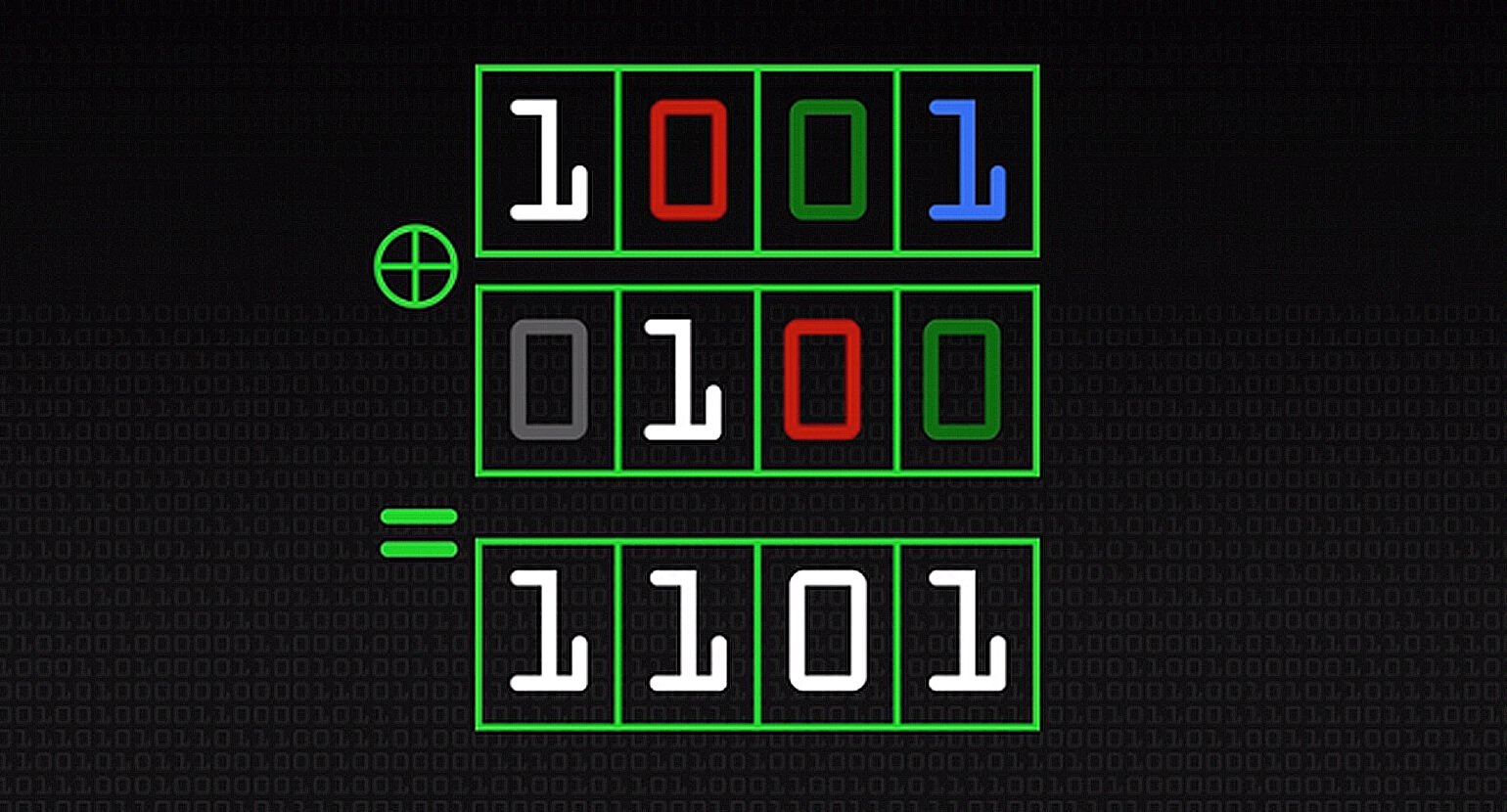
Значение освободившегося бита рассчитывается с помощью линейной булевой функции, в качестве аргументов которой можно использовать все или некоторые значения битов регистра. Очень часто в LFSR используется операция xor — исключающее «или», сложение по модулю 2, — которая обозначается знаком ⊕.

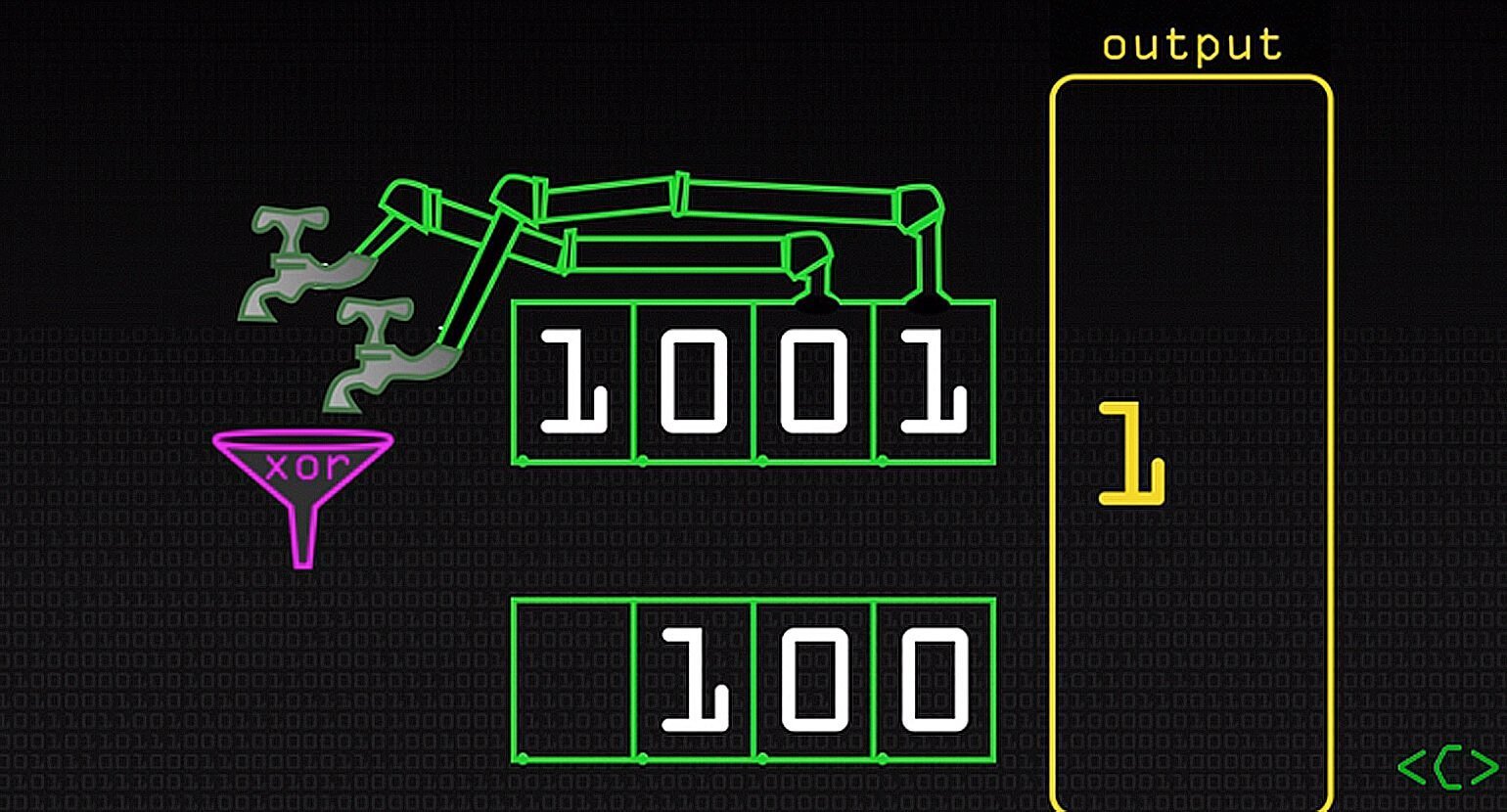
Рассмотрим работу генератора на примере регистра длиной 4 бита. Назовём биты b0, b1, b2, b3. Каждый из битов может принимать значение 0 или 1.

Зададим начальное значение случайным образом, например:

b0	b1	b2	b3
1	0	0	1

Это будет первое состояние регистра.

Сдвинем содержимое регистра вправо на один бит. Получим:

b0	b1	b2	b3
-	1	0	0

Единица из бита b3 потерялась, а b0 освободился.

Так как это линейный регистр с обратной связью, нам нужно определить функцию, которая будет вычислять значение освободившегося бита. Пусть в нашем регистре используется функция b2 ⊕ b3. Биты b2 и b3 в LFSR называются отводами.

Функция вычисляется так:

b2	b3	b2 ⊕ b3
0	0	0
0	1	1
1	0	1
1	1	0

Как видим, результат выполнения битовой операции xor в случае двух переменных равен 1, когда одна из переменных равна 1, а другая — 0. Если обе переменные имеют одинаковое значение, результат равен 0.

Новое значение бита b0 рассчитывается до сдвига и записывается в ячейку только после сдвига. Освободившийся бит будет рассчитываться так: 0 ⊕ 1 = 1 (значения b2 и b3 из первого состояния регистра).

Второе состояние нашего регистра будет таким:

b0	b1	b2	b3
1	1	0	0

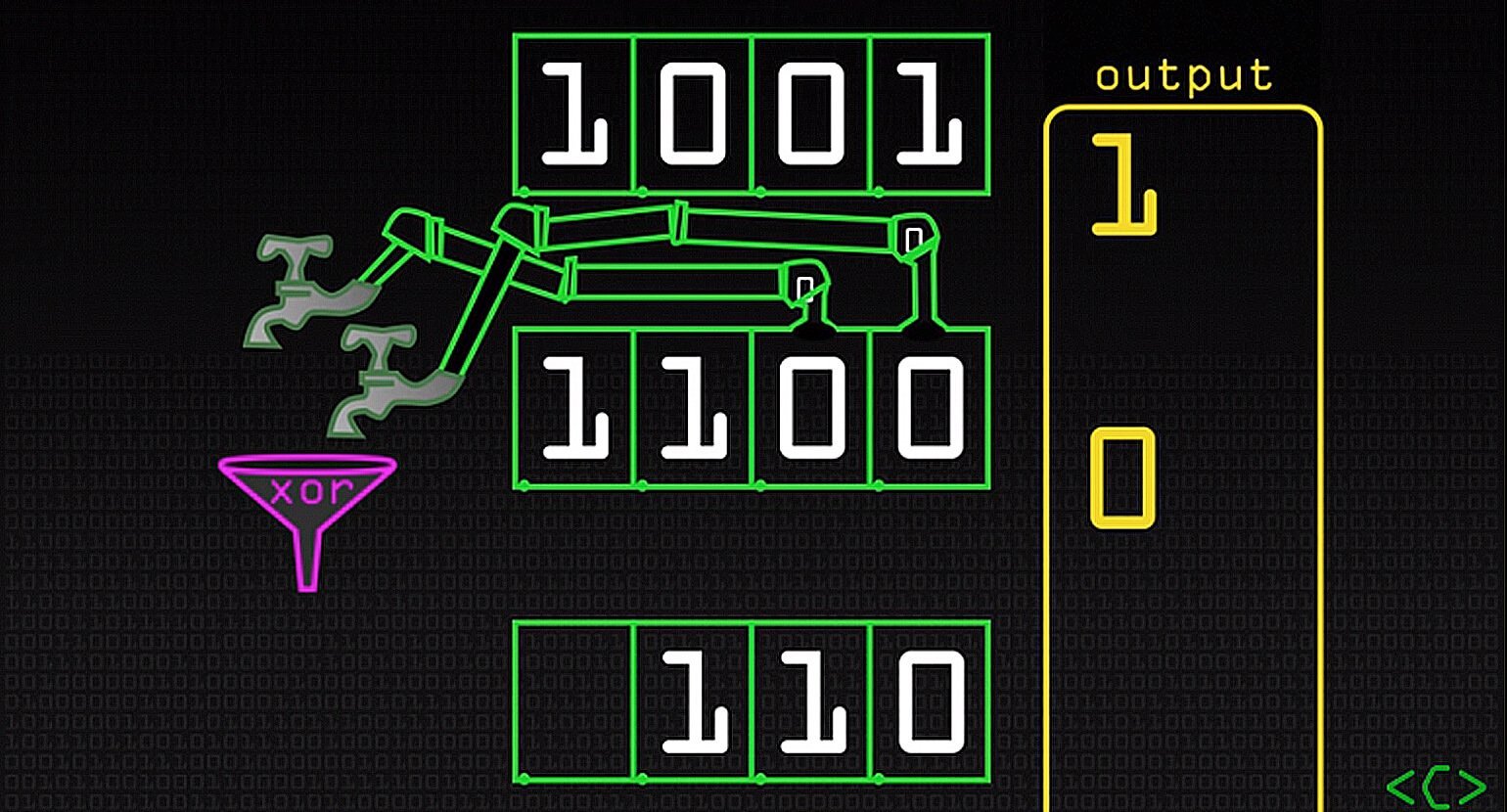
Аналогично, чтобы получить третье состояние, сдвигаем биты влево:

И получаем:

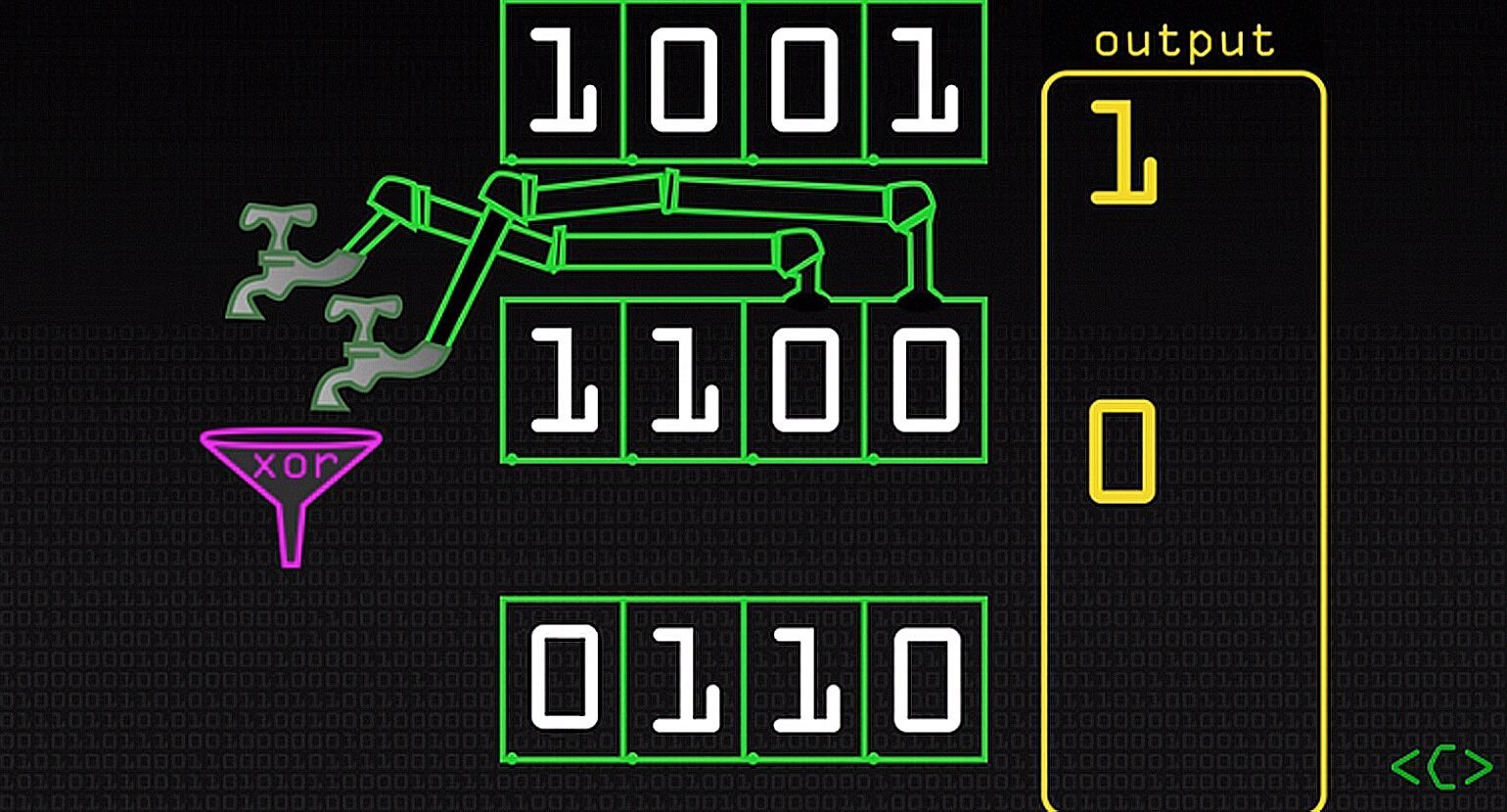
Таких состояний довольно много. И вот что мы получим в результате:

В конце концов мы вернулись к первоначальному состоянию регистра — 1001.

А теперь справа подпишем значения, которые были выведены из регистра.

Фактически это результат работы нашего генератора.

Можно заметить, что было состояние, в котором регистр состоял из одних единиц, но не было полностью нулевого состояния (0000). Дело в том, что в этом случае при любом количестве сдвигов мы бы не получили ничего интересного:

0 ⊕ 0 = 0

Нули так и остались бы нулями. Поэтому сдвиговому регистру всегда нужно присваивать ненулевое начальное значение.

У нас получилось 15 состояний — максимальный период для нашего сдвигового регистра. Генератор выдал все возможные комбинации нулей и единиц.

В общем случае для регистра из n бит максимальный период составляет 2ⁿ – 1.

Теперь рассмотрим другой пример. Пусть функция, вычисляющая освободившийся бит, выглядит так:

b0 ⊕ b2 ⊕ b3

А вычисляется таким образом:

b0	b2	b3	b0 ⊕ b2 ⊕ b3
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Как мы видим, функция равна единице там, где единице равно нечётное число аргументов, и нулю — в противном случае. На мой взгляд, здесь происходит гораздо больше интересного. Возьмём то же самое первоначальное заполнение регистра.

Состояние 1:

b0	b1	b2	b3
1	0	0	1

b0 ⊕ b2 ⊕ b3 = 0

Сдвинем биты вправо и подставим в освободившуюся ячейку вычисленное значение, равное 0.

Состояние 2:

b0	b1	b2	b3
0	1	0	0

b0 ⊕ b2 ⊕ b3 = 0

Состояние 3:

b0	b1	b2	b3
0	0	1	0

b0 ⊕ b2 ⊕ b3 = 1

Состояние 4:

b0	b1	b2	b3
1	0	0	1

Цикл закончился, регистр вернулся к первоначальному состоянию. Это означает: если у вас есть какое-то состояние и правило перевода, то вы всегда сможете перейти в то же состояние, которое было у вас раньше.

Есть математические способы выбора отводов таким образом, чтобы они могли давать максимальный период для регистра определённой длины. Но здесь мы их рассматривать не будем.

Самое классное в таких генераторах — их очень легко программировать. Правда, программы получаются не слишком эффективными, так как много времени тратится на циклы и перестановки, выполняется множество операций xor.

Программы работают медленно, поэтому регистры LFSR часто выполняют в виде электрической схемы, состоящей из дискретных элементов — триггеров, или интегрируют в микросхему.

Для примера напишем программу для нашего 4-битного генератора. Сделаем это на Python — в нём много битовых функций, и он позволяет работать с целыми числами произвольной длины.

Возьмём условия из первого примера:

первоначальное значение регистра — 1001;
функция, вычисляющая освободившийся бит, — b2 ⊕ b3.

Значение освободившейся ячейки будем рассчитывать следующим образом:

Найдём результат операции xor над текущим состоянием регистра и состоянием, когда он сдвинут на одну позицию вправо:

Нам нужен последний бит результата — это и будет b2 ⊕ b3:

Наша программа будет выглядеть так:

state = 0b1001 # задаём первоначальное значение регистра


for i in range(20): # для примера рассчитаем 20 состояний регистра
    print("{:04b}".format(state)) # вывод состояния на печать
    newbit = (state ^ (state >> 1)) & 1  # рассчитываем новое значение освободившегося бита 
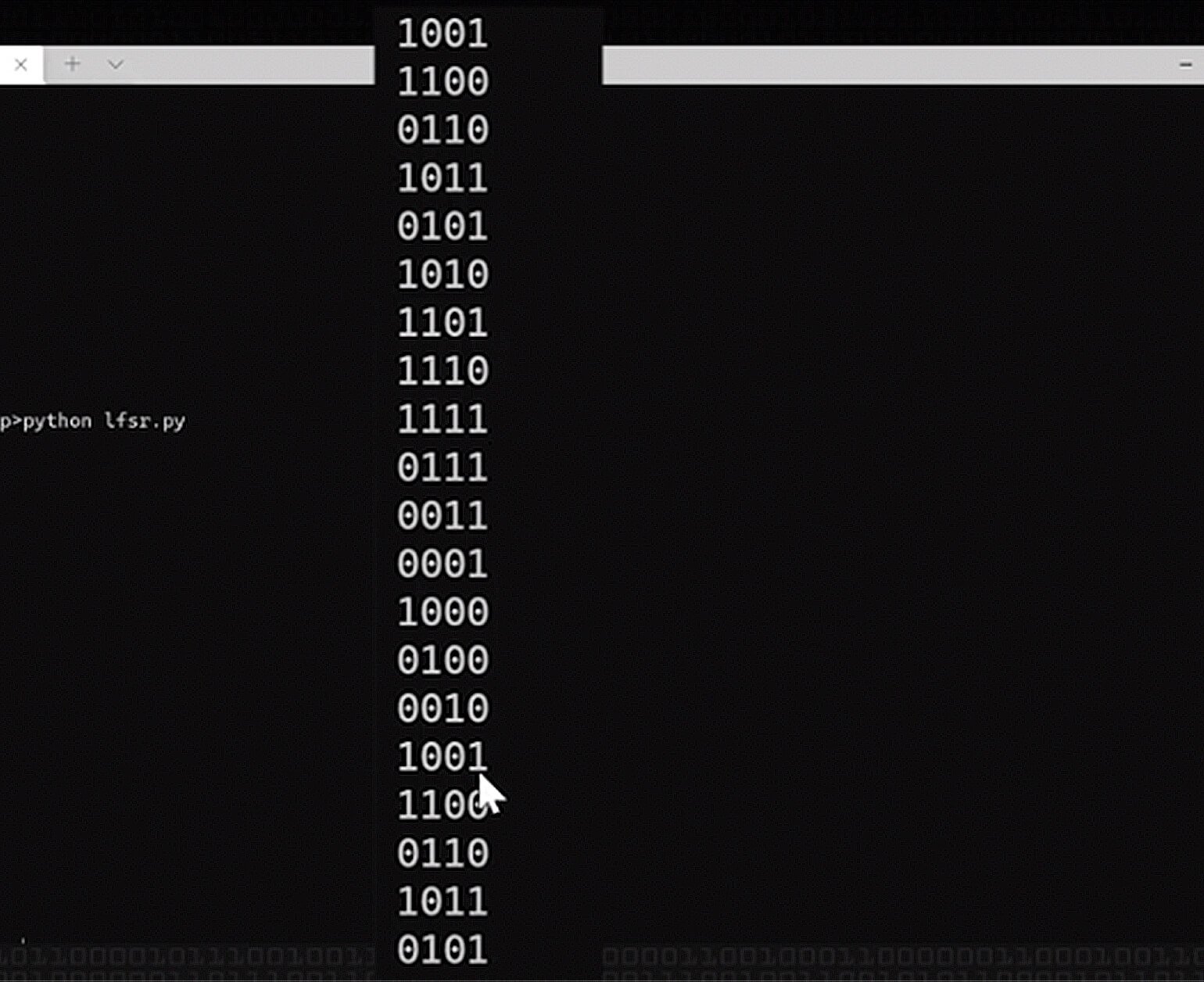
    state = (state >> 1) | (newbit << 3) # новое состояние регистра: сдвигаем содержимое вправо и вставляем в первую позицию слева новый бит

Запустим программу и рассмотрим результат:

Мы видим, что с 16-й позиции генерация значений зациклилась.

Если вы используете LFSR в качестве генератора случайных чисел, то не обязательно распечатывать каждое состояние полностью, так как между итерациями оно не сильно меняется: содержимое регистра сдвигается вправо, меняется только левый бит. Каждый раз оно будет выглядеть очень похоже.

Вместо того чтобы выводить всё состояние целиком, выведем на печать только последний бит. Программа будет выглядеть так:

state = 0b1001    
for i in range(20):   
    print(state &1, end = '')  
    newbit = (state ^ (state >> 1)) & 1 
    state = (state >> 1) | (newbit << 3)

В результате получим псевдослучайную битовую последовательность:

10011010111100010011

Созданный нами 4-битный сдвиговый регистр можно использовать в качестве небольшого генератора случайных чисел, но для создания потокового шифра он не годится — слишком мал.

Рассмотрим ещё один пример — создадим регистр, подходящий для потокового шифра. Увеличим число разрядов регистра до 128, а в качестве начального значения зададим 128-значное число, у которого левый и правый биты равны единице, остальные — нулю.

Сделаем бесконечным количество итераций и будем останавливать программу, когда захотим. Максимальный период 2¹²⁸ – 1 для нашего сдвигового регистра даст операция xor над битами номер 0, 1, 2, 7 справа.

Исправим нашу программу:

state = (1 << 127) | 1    
while True:   
    print(state &1, end = '')  
    newbit = (state ^ (state >> 1) ^ (state >> 2) ^ (state >> 7)) & 1 
    state = (state >> 1) | (newbit << 127)

Запустим программу и получим такой результат:

Вы спросите: когда цикл повторится? Мой компьютер выдаёт на экран около миллиона бит в секунду. Вероятно, нам придётся ждать повторения цикла в 1020 раз дольше, чем существует Вселенная.

Такие системы используются для генераторов случайных чисел. Статистическая вероятность этих потоков очень хорошая — приблизительно как случайное подбрасывание монеты. Но криптографически они не слишком безопасны — если у вас есть большая часть потока, то вы можете решить множество линейных уравнений и найти числа, которые его сгенерировали, а затем сгенерировать следующий поток. То есть вы взломаете шифр.

Существуют разные способы повышения криптоустойчивости генераторов — например, использование нескольких регистров LFSR. Числа, которые они выдают, становятся аргументами булевой функции, а результаты работы этой функции используются для шифрования. Также возможно использование нелинейной комбинации прямой и обратной связи в регистре — так работает шифр Trivium.

Регистры LFSR очень быстры в аппаратной реализации, поэтому их часто используют в маломощных устройствах, например в смарт-картах.

Читайте также: