Математика для джунов: что нужно повторить перед собеседованием по Data Science
Говорят, что всю математику знают только Бог и Григорий Перельман. Но джуниору на собеседовании вся и не нужна.

Возможно, наступит время, когда дата-сайентисту вообще не нужно будет знать математику, а вся работа сведётся к нажатию на кнопку Analyze data. Но пока для начала карьеры в Data Science требуется знать хотя бы базовые математические понятия.
Причина простая: уровень соискателей-джуниоров примерно одинаков. Поэтому из двух кандидатов скорее выберут знакомого с принципами, на которых построены инструменты анализа данных, машинного обучения и глубокого обучения.
Мы отобрали семь фундаментальных тем из вопросов к собеседованиям на вакансию Junior Data Scientist:
- по теории вероятностей,
- линейной алгебре,
- математическому анализу,
- математической статистике.
И написали к ним краткие ответы-шпаргалки. Держите!
1. Закон больших чисел: всё усредняется
Сложность: 1/3
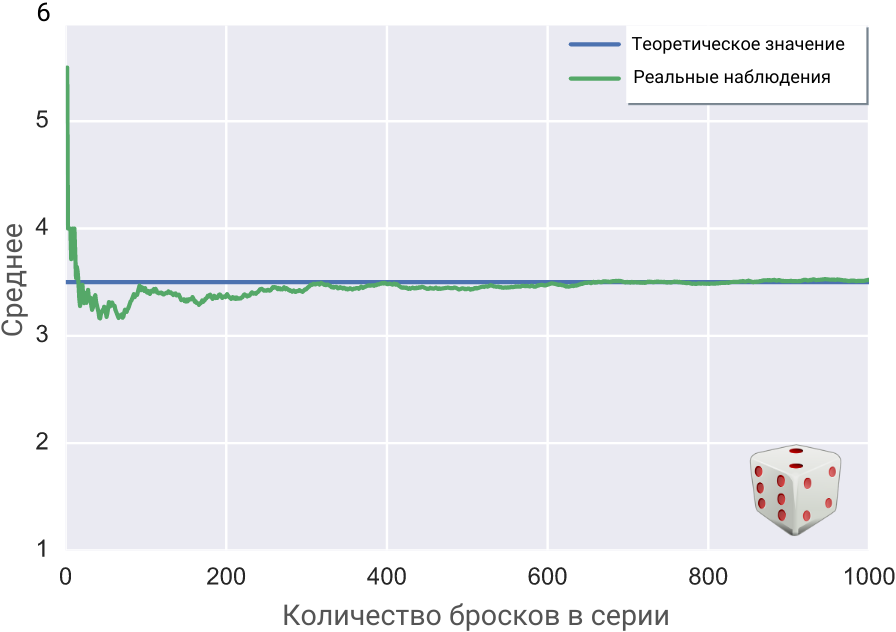
Бросим игральный кубик десять раз. Затем запишем среднее значение всех десяти бросков: сложим все выпавшие очки и поделим на 10.
После этого подбросим снова, но теперь уже серией из двадцати бросков, и также запишем среднее. Сумму выпавших очков поделим на 20.
Закон больших чисел утверждает, что при увеличении количества бросков от серии к серии среднее арифметическое всех выпавших в ней очков будет стремиться к определённому числу, которое называется математическим ожиданием.
Для игрального кубика оно равно среднему арифметическому очков на его шести гранях: (1 + 2 + 3 + 4 + 5 + 6) / 6 = 21 / 6 = 3,5.
Для других случайных величин математическое ожидание будет вычисляться иначе, но суть останется та же: при увеличении количества реальных попыток случайная величина усредняется. А точнее, стремится к своему теоретически вычисленному ожидаемому значению. Закон, таким образом, связывает реальность и теорию.
Для Data Science этот закон настолько фундаментален, что кажется абсолютно очевидным: чем больше данных, тем точнее предсказание. Впору переименовывать его в «Закон больших данных».
2. Матрица — это преобразование
Сложность: 1/3
Внешне матрица — это прямоугольная таблица из m строк и n столбцов, состоящая, как правило, из чисел. Если в матрице только одна строка или только один столбец, то получается вектор. Вектор — это тоже матрица.
Матрицы можно умножать на число, а матрицы одинакового размера — ещё и складывать между собой поэлементно. Умножение матрицы на матрицу сложнее, чем умножение чисел, и лучше всего постигается в упражнениях. Главное — помнить, что строка умножается на столбец и что менять местами две умножаемых матрицы нельзя.
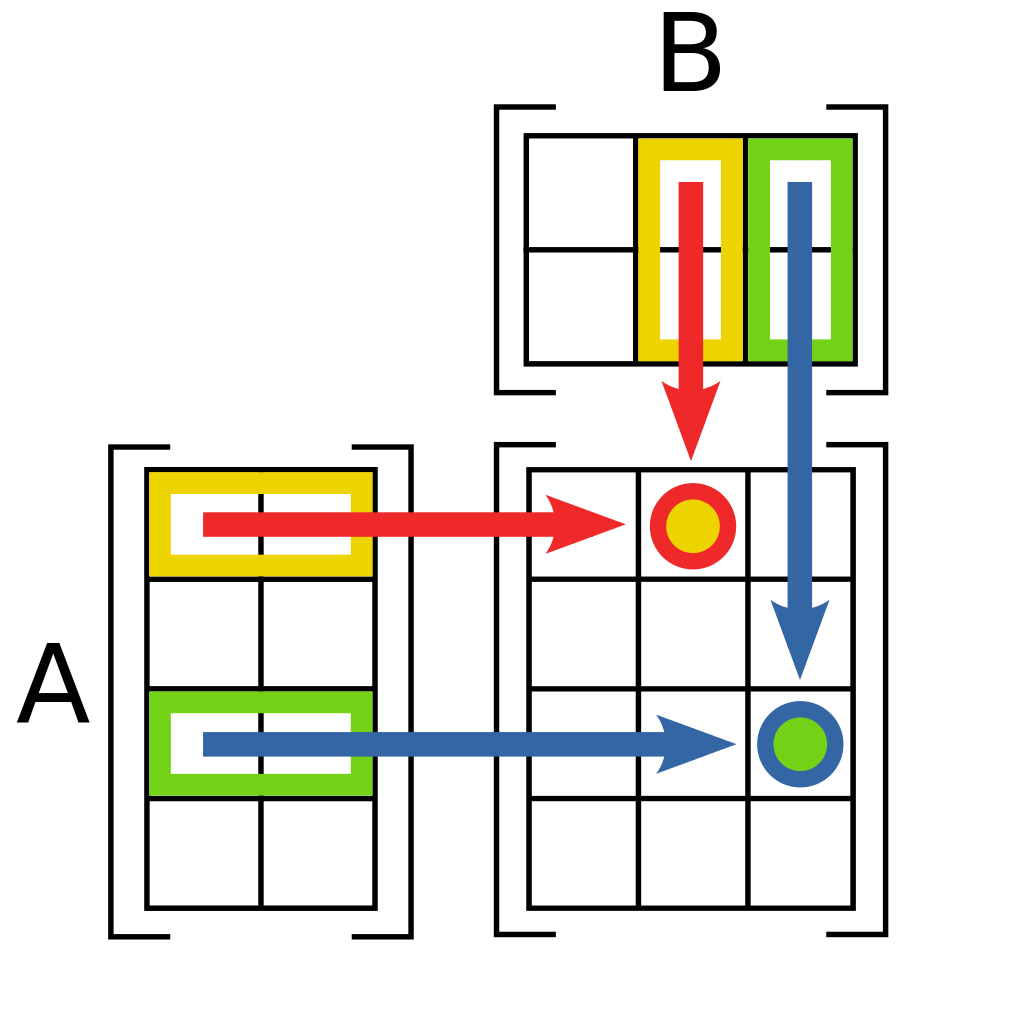
Матрицу правильнее всего понимать как «численный протокол» некоего преобразования. Например, чтобы преобразовать один вектор в другой, нужно умножить его на соответствующую матрицу. Более сложные преобразования тоже задаются или матрицами, или похожими на них объектами, например тензорами (которые сами состоят из матриц).
В Data Science без векторов и матриц никуда. Например, метод главных компонент, который применяют, чтобы избавиться от лишних данных, использует вычисление собственных векторов матриц. А латентно-семантический анализ, необходимый для «понимания» машинами смысла слов, основан на преобразовании матриц и вычислении скалярного произведения векторов.
3. Градиент — это направление
Сложность: 2/3
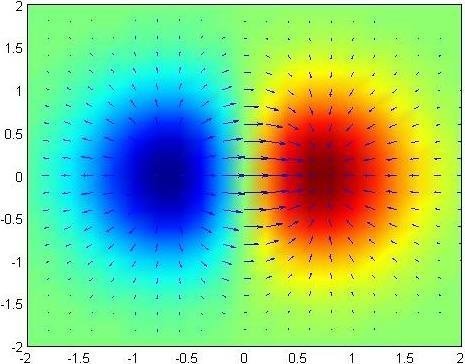
Градиент, если простыми словами, это вектор-указатель. Стрелка указывает в направлении наибольшего роста какой-нибудь величины, а длина этого вектора соответствует скорости роста этой величины.
Векторы обычно рассматривают не в одной точке: точками покрывают сразу весь интересующий участок — и на нём уже рисуют градиенты. Если к этому добавить цвет, чтобы подчеркнуть размеры и направленность векторов, то получаются занятные абстрактные композиции.
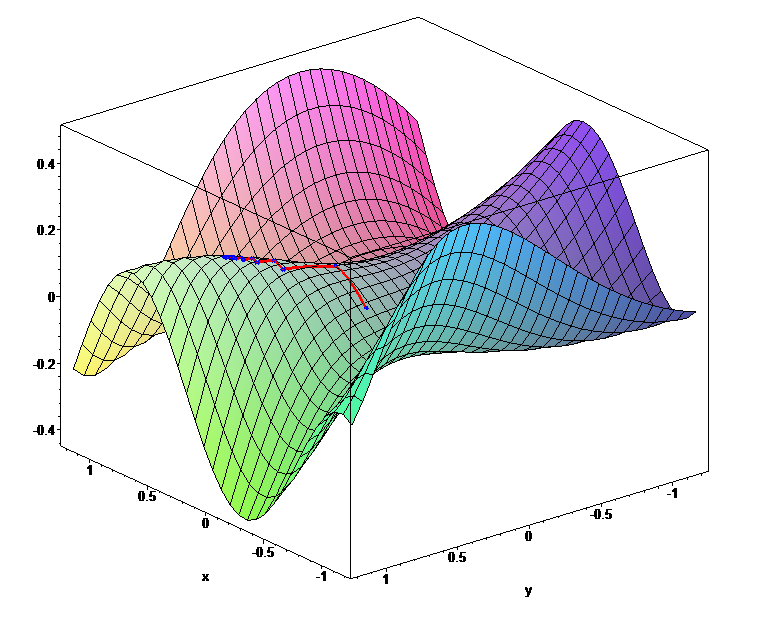
В deep learning процесс обучения нейросети состоит в том, что мы много-много раз меняем вес каждого нейрона (его авторитет) в зависимости от размера ошибки, которую он передал нейронам следующего слоя. Совокупность величин этих ошибок образует поверхность в многомерном пространстве весов. Задача — найти минимум этой поверхности, то есть «яму» или «ложбину», где ошибки будут наименьшими.
Чтобы найти этот минимум, и нужен градиент. Он, правда, указывает в сторону максимума, но ничто не мешает идти в прямо противоположном направлении — спускаться в направлении антиградиента. Поэтому класс этих методов и называется градиентным спуском.
4. Теорема Байеса: следствие указывает причину
Сложность: 1/3
Эта теорема говорит, насколько нужно изменить ожидания, когда мы узнаём новый факт или наблюдаем новое свидетельство.
Условие задачи: Энтомолог нашёл жука с узором на корпусе и надеется, что это редкий подвид. Надежда его основана на том, что жуки редкого подвида в 98% случаях с узором, а среди обычных жуков узор имеют только 5%. Редкий подвид действительно редок: таких жуков всего 0,1% от всей популяции.
Вопрос: Какова вероятность, что найденный жук с узором относится к редкому подвиду?
Теорему Байеса и связанную с ней формулу полной вероятности лучше всего изучать на задачах, подобных этой. Самое сложное, что вас ждёт, — это вычисление дробей и рисование древовидных диаграмм. По этой ссылке можно посмотреть и доказательство формулы, и несколько примеров.
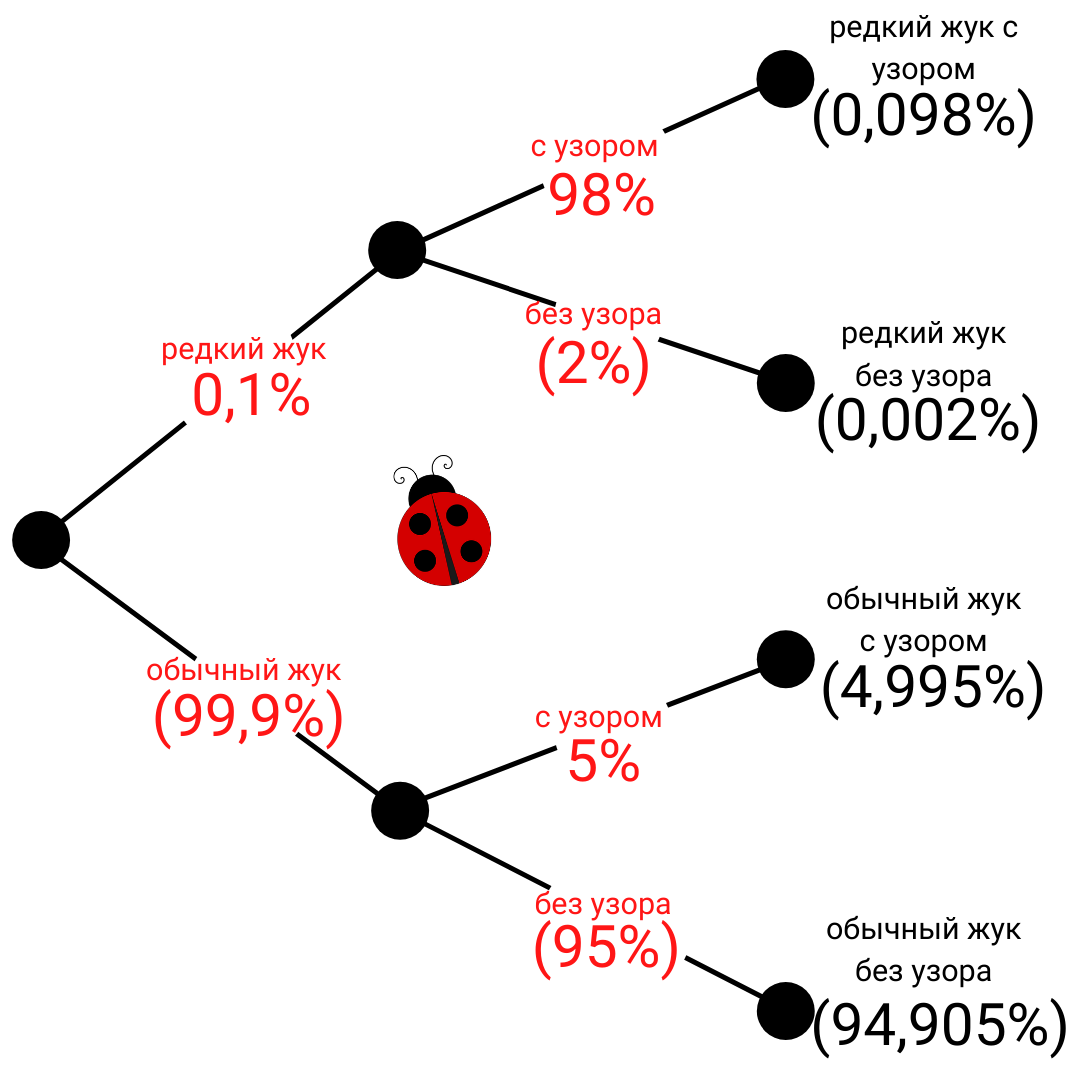
Оценка потенциального заёмщика (кредитный скоринг), определение точности медицинского теста, поиск признаков банковского мошенничества (антифрод) или взлома корпоративной сети — все эти прикладные задачи Data Science используют байесовский подход.
5: Распределение: главное — график
Сложность: 1/3
Распределение — просто закон соответствия одной величины другой. Например, в теории вероятностей, где появился этот термин, это было соответствие между значением случайной величины и вероятностью того, что она примет это значение.
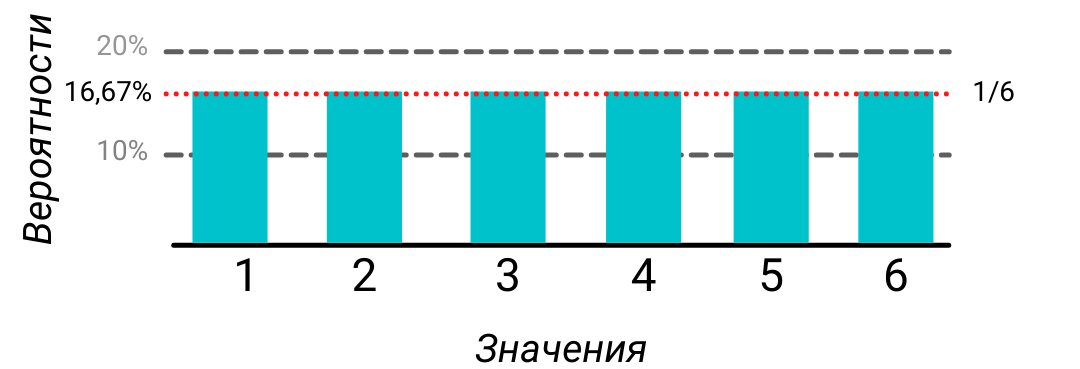
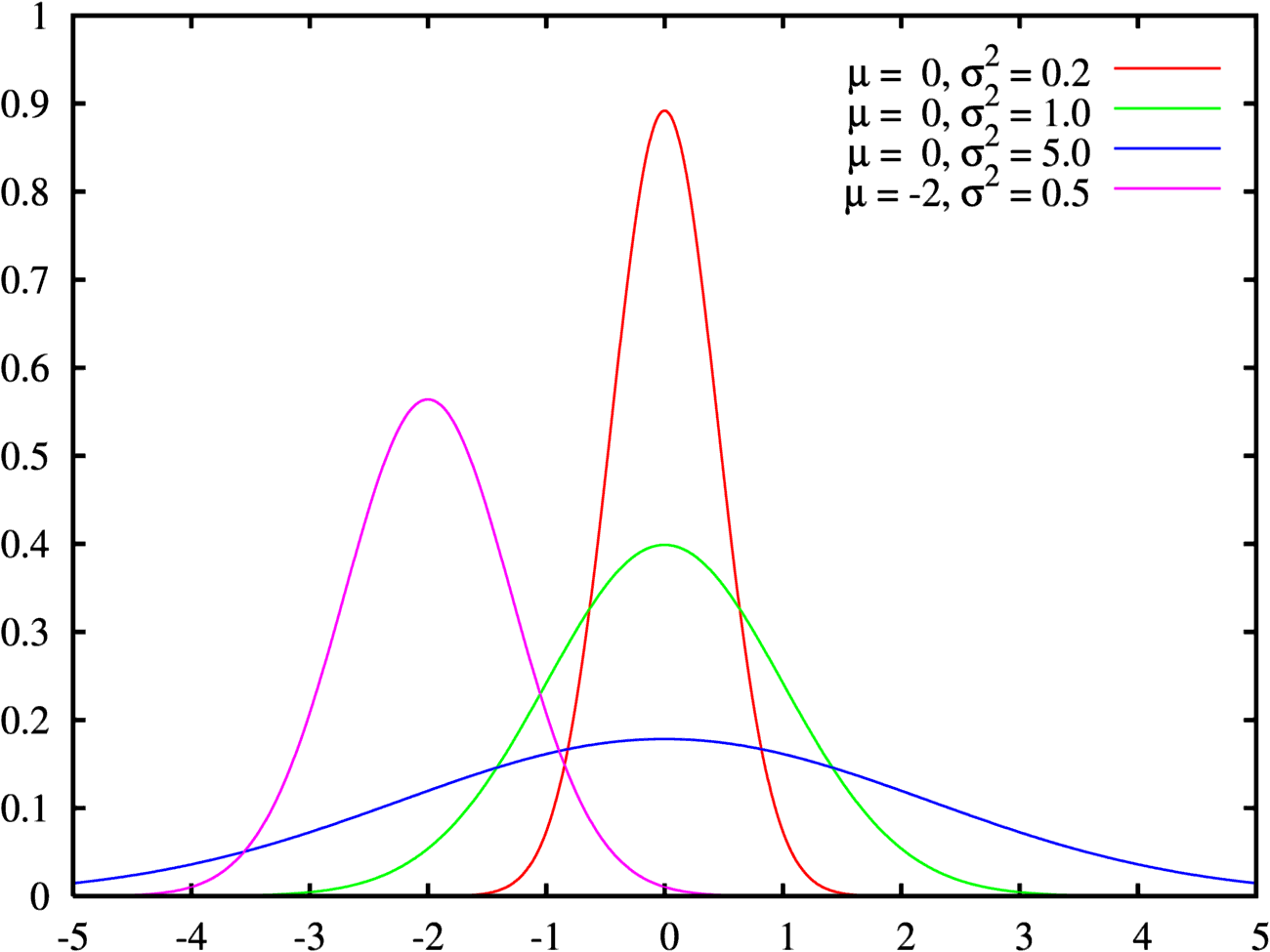
Но дата-сайентисту распределения требуются не для вероятностей, а чтобы понять, какой именно процесс скрывается за данными. Поэтому ему (то есть вам) нужно запомнить названия, графики и параметры всех основных распределений, благо их не так много.
Например, у знаменитой гауссианы, или нормального распределения, есть всего два параметра, которые влияют на форму графика: μ (произносится «мю»), двигающий «колокол» вправо-влево, и σ (сигма) — определяющий одновременно и ширину, и высоту.
Так что если график ваших данных внешне напоминает какое-нибудь распределение, то первым делом нужно подогнать параметры в формуле этого распределения так, чтобы его итоговый вид примерно совпадал с вашими данными. Если это удалось, тогда то, что вы сделали с данными, называется регрессией.
6. Регрессия: от разного к средним
Сложность: 1/3
Регрессия, простыми словами, это закон, определяющий соотношения между средними значениями каких-либо величин. Например, средний рост сыновей линейно зависит от среднего роста отцов: чем выше средний рост отцов, тем выше и средний рост сыновей.
В Data Science регрессия возникает в задаче исследования реальных данных, которые визуально часто выглядят как группы точек на координатной плоскости.
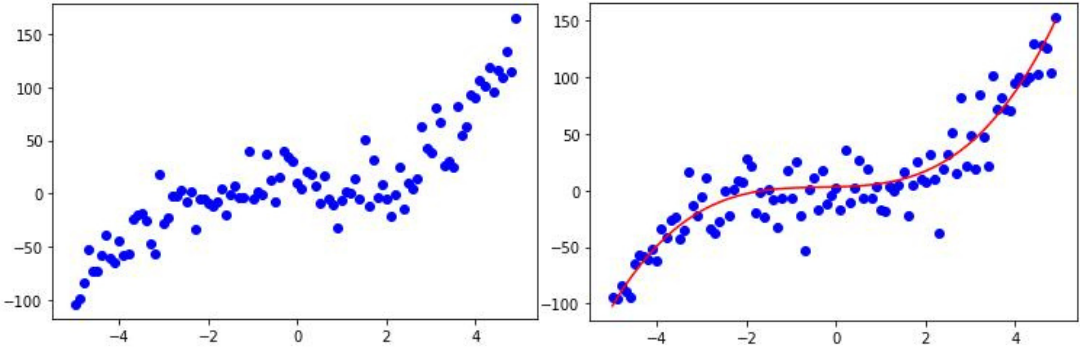
Если через эти точки можно провести линию, которая соответствует их общему тренду и не слишком далека от каждой из них, говорят, что формула, задающая эту линию, аппроксимирует (приближает) данные.
Иными словами, в задачах регрессии мы заменяем (аппроксимируем) реальные значения средними и исследуем соответствие уже между ними. Это не только проще для вычислений, но и даёт основания для прогноза и предсказаний. А дата-сайентиста хлебом не корми — дай что-нибудь предсказать.
7. Статистическая значимость — порог доверия
Сложность: 2/3
Статистически значимая величина — это «скорее всего, неслучайная» или «маловероятно, что случайная» величина. Мера случайности и неслучайности определяется по-разному, но всегда заранее.
Статистическая значимость используется при проверке статистических гипотез. Например, мы предположили, что зелюки в основном хрюкочут. Это будет нашей основной статистической гипотезой. Альтернативной гипотезой будем считать, что зелюки в основном не хрюкочут, а пыряются. И договоримся, что величина статистической значимости будет, например, 5%.
Возьмём результаты наблюдения за зелюками. Если хрюкочущих зелюков в них окажется 95% или больше, будем говорить, что основная гипотеза прошла статистическую проверку при уровне значимости α (альфа) = 0,05. А количество альтернативных (пыряющихся) зелюков не оказалось статистически значимой величиной.
Другими словами, уровень α — это вероятность отклонить основную гипотезу. Если гипотеза истинна, то есть в реальности зелюки действительно в основном хрюкочут, это ещё и вероятность совершить ошибку первого рода — ошибочное отвержение, или ложную тревогу. Если гипотеза неверна и зелюки таки больше пыряются, чем хрюкочут, то величина α — это вероятность не отвергнуть ложную гипотезу и допустить ошибку второго рода, которую называют ошибочным принятием или пропуском события.
Собеседование не предел
«Математику уже затем учить надо, что она повышает шансы на оффер», — гласит старинная поговорка дата-сайентистов.
По неведомым науке причинам математика удивительно эффективна на собеседованиях: придаёт уверенности словам, располагает к вам интервьюеров и повышает ваш авторитет в глазах людей, совершенно с ней незнакомых. Есть даже подозрения, что существует мировой заговор математиков, которые: а) проникли везде и всюду; б) поддерживают друг друга всегда и во всём.