Как решать линейные уравнения: правила, примеры и пошаговые алгоритмы

Линейные уравнения звучат скучно только в школьных задачниках. На деле они встречаются повсюду: от простых покупок до сложных моделей в программировании и науке. Например, вы покупаете в магазине 3 шоколадки по 50 рублей. Попытка найти общую сумму покупки — уже уравнение.

В этой статье рассказываем всё про линейные уравнения: какие они бывают, сколько в них может быть неизвестных, что называют корнем уравнения и как его найти.

Содержание

• Что такое линейное уравнение
• Виды линейных уравнений
• Свойства линейных уравнений
• Решение линейных уравнений
• Частые ошибки при решении линейных уравнений
• Где применяются линейные уравнения

Что такое линейное уравнение

Линейное уравнение — это уравнение, в котором переменная не умножается сама на себя и не находится под корнем или в знаменателе. Переменная — это неизвестное число.

Простейшее линейное уравнение выглядит так:

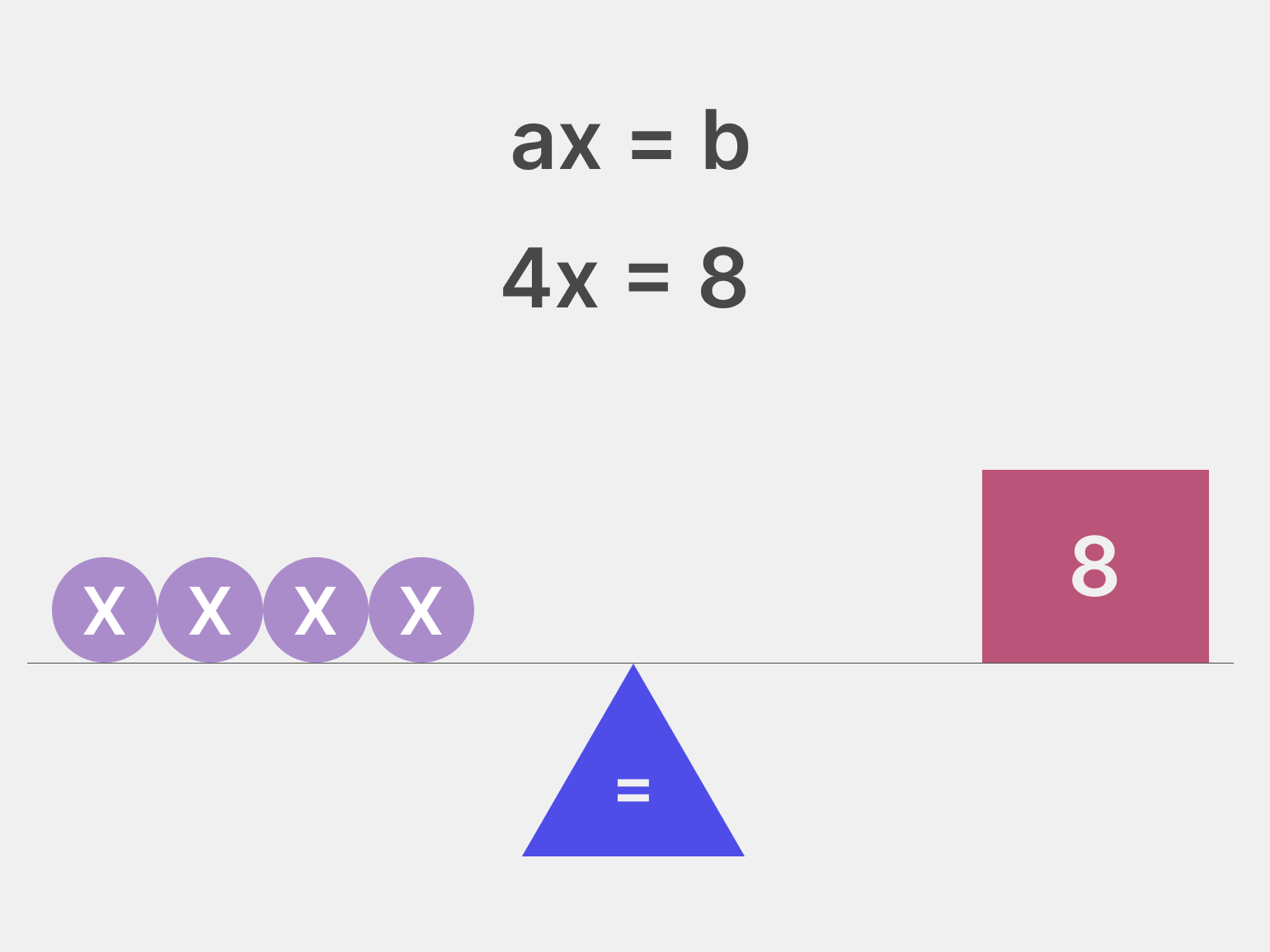
В линейном уравнении выше a и b — это числа, а x — неизвестная переменная. Переменную ещё называют корнем уравнения, а в математике часто можно встретить задачу «найти корень уравнения».

Корень линейного уравнения — это число, которое уравнивает две стороны уравнения — a * x и b. Например, если b = 2, то и a * x тоже должно равняться 2. Но если никак не получается уравнять две стороны, то обычно говорят: корней нет.

Виды линейных уравнений

Линейные уравнения бывают разных видов: с множеством чисел, с одной или несколькими переменными (корнями) и другие. Рассмотрим самые известные из них.

Простое представление линейного уравнения с одной переменной:

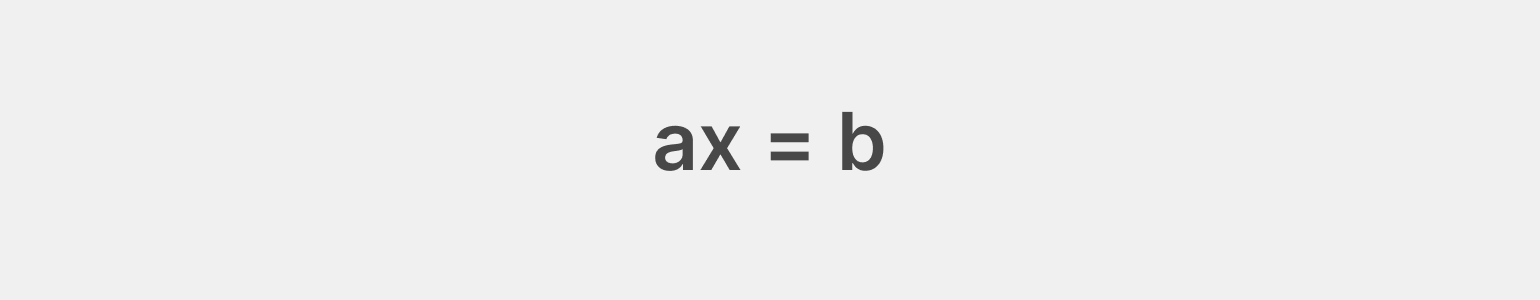
Формула решения такого уравнения выглядит так:

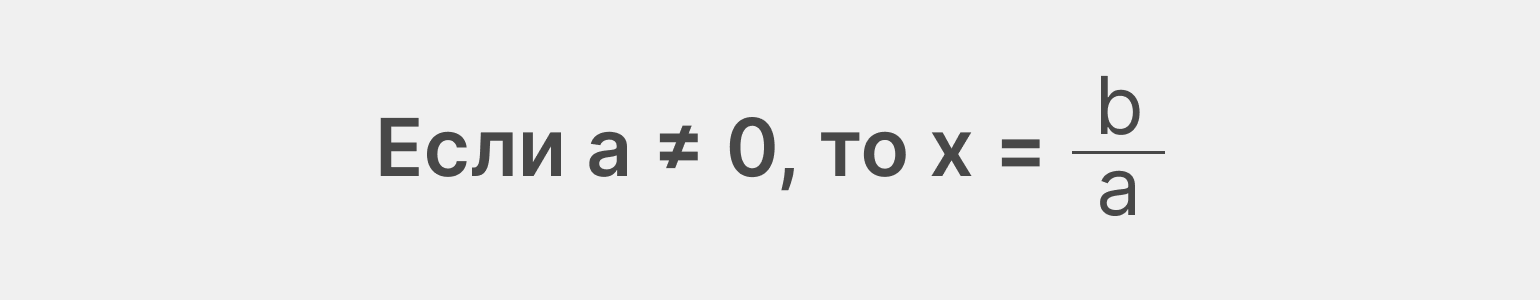
Важно учесть, что, так как мы b делим на a, a не должно быть равно нулю, потому что на 0 делить нельзя.

Это применимо и к следующей расширенной вариации линейного уравнения с двумя числами и нулём:

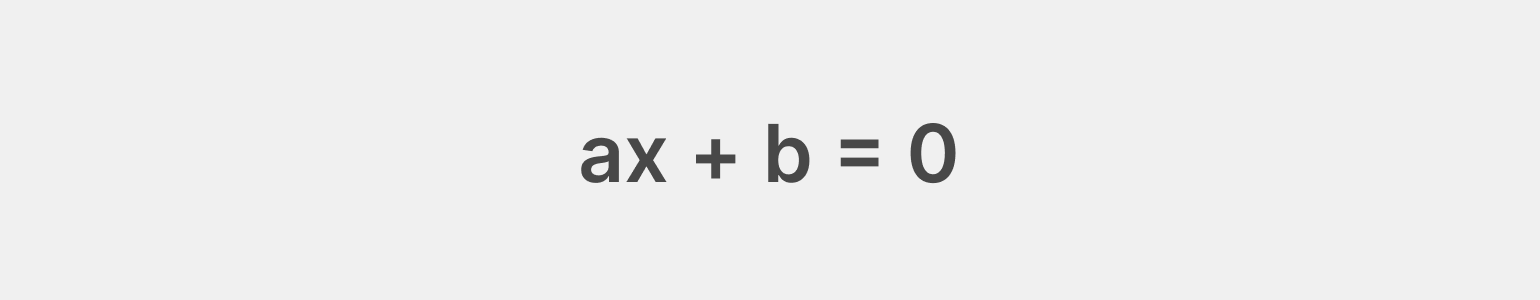
Найти корень такого уравнения можно с помощью следующей формулы:

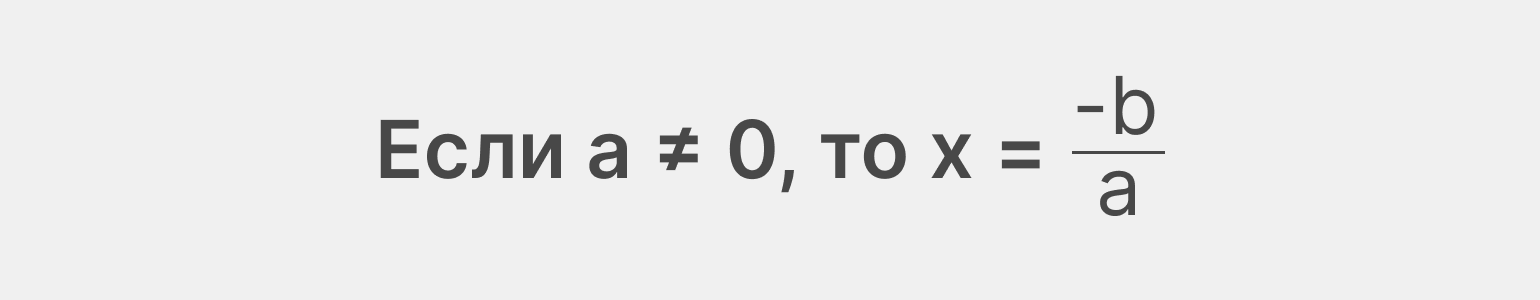
Формула похожа на предыдущую, но мы делим отрицательное число b на a, потому что при решении такого уравнения b переносится из левой в правую часть и меняет свой знак на противоположный.

Существует общее линейное уравнение с тремя числами a, b, c и одной переменной x. Такое уравнение называют линейным уравнением общего вида:

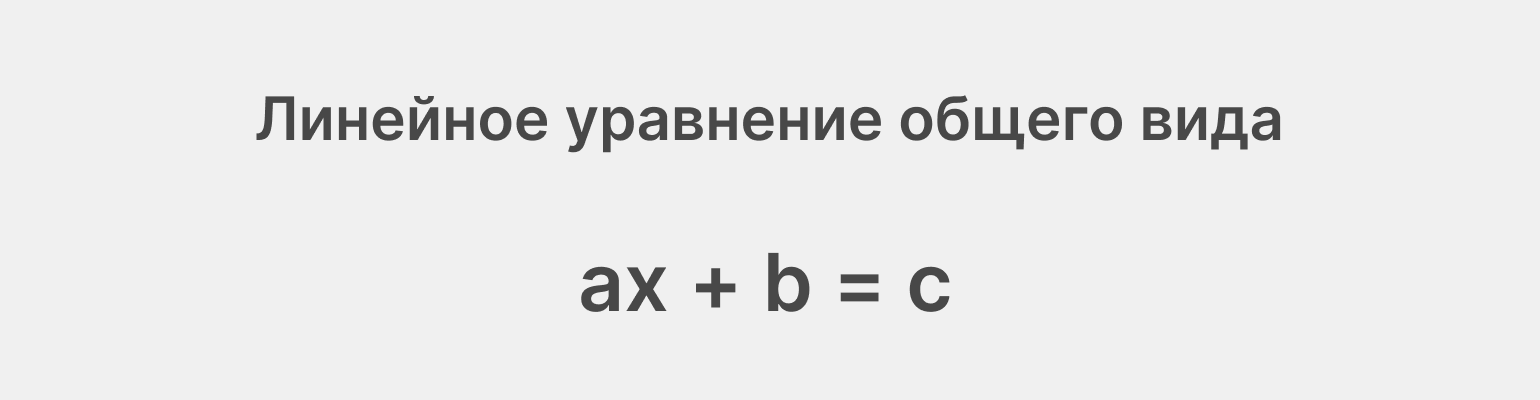
Формула для его решения выглядит так:

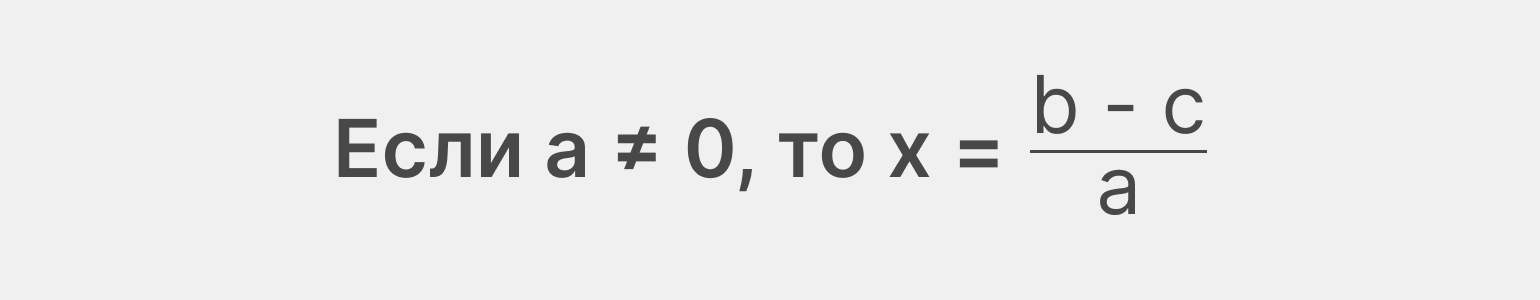
Свойства линейных уравнений

Способы решений и свойства линейных уравнений с одной неизвестной переменной тесно перекликаются. Из всего, что сказано выше, можно вынести следующие правила:

• Если a ≠ 0, то уравнение имеет одно решение x = b / a.
• Если a = 0 и b = 0, то уравнение имеет бесконечное множество решений.
• Если a = 0, а b ≠ 0, то уравнение не имеет решений.

Кроме того, у линейных уравнений есть следующие свойства:

• В линейном уравнении нет корней или степеней — переменная x всегда представлена в первой степени. То есть переменная не может иметь следующий вид: x², √x, 1/x.
• При переносе элементов с одной стороны в другую через знак равенства знак меняется на противоположный. Например: 2x + 4 = 6 → 2x= 6 − 4.
• Обе части линейного уравнения можно разделить или умножить на одно и то же число, при этом корень уравнения не изменится.
• Любое линейное уравнение с одной неизвестной переменной можно привести к виду ax = b.

Все изученные свойства мы далее применим на практике.

Решение линейных уравнений

Пример 1

Найдите корень уравнения 2x = 6.

Решение

Решением этого уравнения будет формула x = b / a:

x = 6 / 2

Если 6 разделить на 2, то получится 3 — это и есть корень уравнения.

x = 3

Проверим равновесие сторон, подставив в x полученное число 3:

2 × 3 = 6

6 = 6

Левая и правая части равны, значит, линейное уравнение решено верно.

Как мы сказали выше в свойствах — левую и правую часть можно разделить или умножить на одно и то же число, чтобы упростить выражение. В этом примере мы можем разделить 2 и 6 на 2.

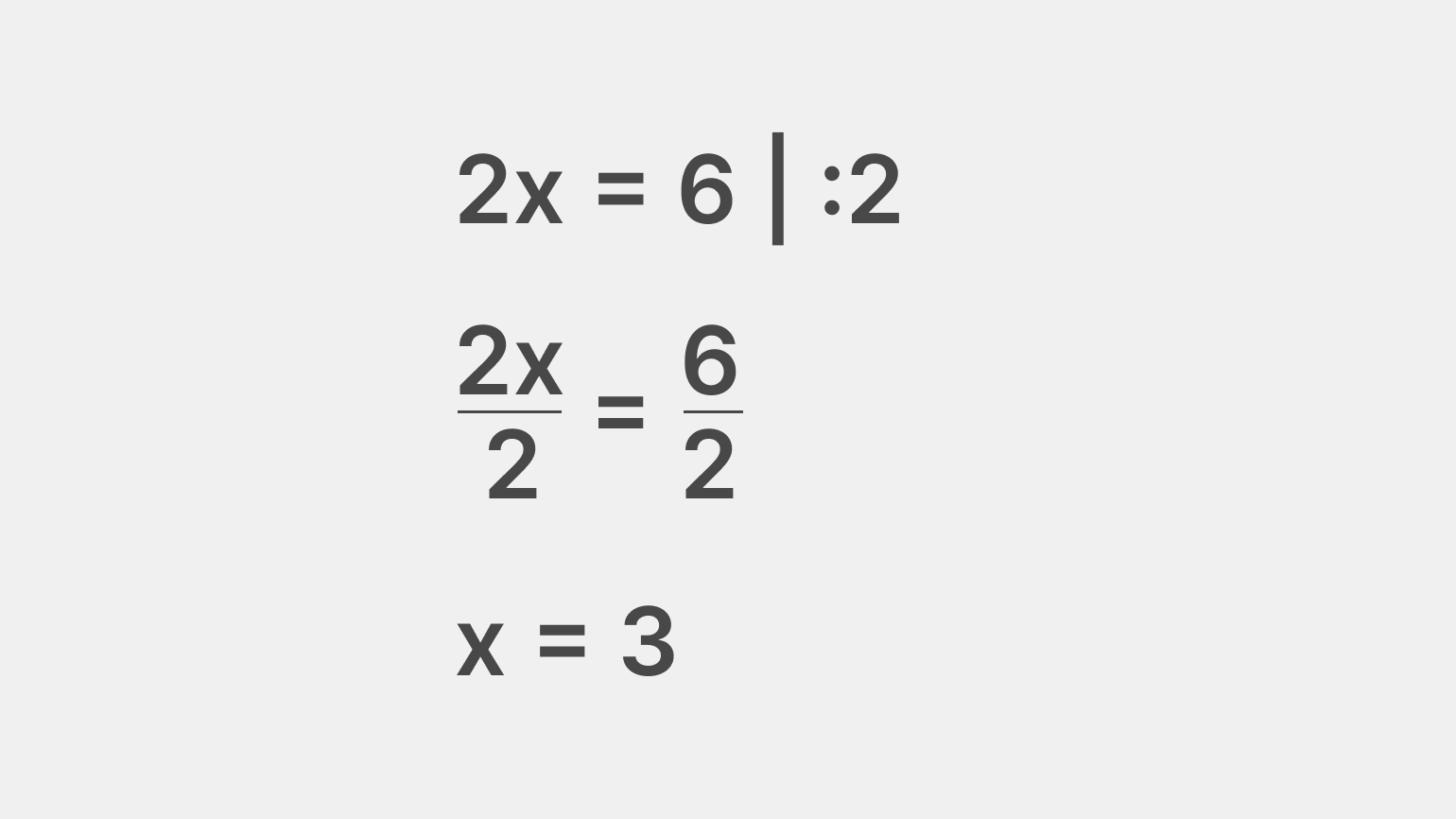
Если разделить 2x на 2, то мы получим 1x, то есть просто x. Если разделим 6 на 2, то получим 3. С помощью этого метода можно упрощать более сложные линейные уравнения.

Пример 2

Найдите корень уравнения 0x = b.

Пример 3

Найдите корень уравнения 0x = 5.

Пример 4

Найдите корень уравнения 2x + 3 = 11.

Пример 5.

Найдите корень уравнения 3x − 5 = 2x + 4.

Частые ошибки при решении линейных уравнений

Рассмотрим распространённые ошибки, которые новички часто допускают при решении линейных уравнений.

Перенос с неправильным знаком

При переносе чисел и переменных из одной части уравнения в другую знак меняется на противоположный. Например, в уравнении x − 5 = 10 при переносе отрицательное −5 станет положительным 5.

x − 5 = 10

x = 10 + 5

x = 15

15 − 5 = 10

10 = 10

Неправильная последовательность действий

В уравнении 2(x + 3) = 4x + 6 можно ошибочно сначала разделить левую и правую часть, а потом раскрыть скобки и решить уравнение вот так:

2(x + 3) = 4x + 6

x + 3 = 2x + 3

x = 0

Значение корня уравнения верное, но ход решения — нет. Даже если в этом случае мы случайно пришли к верному значению, в другом примере такая логика поломает весь пример и приведёт к путанице.

Правильно сначала раскрыть скобки, а потом уже делить все стороны. То есть вот так:

2(x + 3) = 4x + 6

2x + 6 = 4x + 6

2x = 0

x = 0

Деление всех частей линейного уравнения

В уравнении выше можно сделать и другую ошибку. Допустим, вы правильно раскрыли скобки:

2(x + 3) = 4x + 6

2x + 6 = 4x + 6

После этого можно сократить запись, разделив обе части уравнения на одно число. Здесь лучше всего разделить на 2, так как все числа разделятся без остатка.

В этом случае надо внимательно производить деление, чтобы ничего не пропустить.

Где применяются линейные уравнения

Рассмотрим, где применяют линейные уравнения:

• В математике линейные уравнения — базовая часть алгебры. Их используют повсеместно, а уравнения с одной переменной — фундамент для более продвинутых тем: линейных уравнений с несколькими переменными, систем уравнений, графиков, функции и других.
• Во многих алгоритмах в основе логики лежат линейные уравнения вида ax + b = c.
• В быту с помощью линейных уравнений можно найти неизвестные данные. Представьте, что вы купили две футболки и отдали за них 3000 рублей. Одна футболка стоит 1200 рублей, а цену второй можно узнать с помощью уравнения.
• В бизнесе с помощью линейных уравнений рассчитывают цены на товары и услуги. Например, клиент сдаёт в службу доставки x коробок. Доставка каждой коробки стоит 50 рублей, и надо ещё заплатить комиссию 2000 рублей. С помощью уравнения можно узнать, сколько всего коробок сможет отправить клиент на определённую сумму.