Иррациональные числа: определение, свойства и примеры

Числами можно описать всё в мире, и мы с вами имеем дело с ними повсеместно. Но есть такие числа, величину которых по сей день невозможно определить точно — они называются иррациональными. Их открыли ещё в VII веке до нашей эры, когда древние математики поняли, что не из всех натуральных чисел можно извлечь квадратный корень.

Сегодня мы узнаем, что такое иррациональные числа, чем они отличаются от остальных, а также посмотрим на них в коде на Python.

Главное об иррациональных числах

• Определение
• Свойства
• Отличия от рациональных чисел
• Использование в геометрии
• Примеры работы на Python
• Повторим пройденное

Валерий Линьков

Эксперт Skillbox по компьютерным сетям и кибербезопасности. Автор телеграм-канала «Кудрявый микрофон».

Иррациональные числа: определение

Иррациональное число — это число, которое невозможно представить в виде дроби m/n, где m — целое число, а n — натуральное. Это определение довольно сухое и формальное — сейчас объясним понятнее.

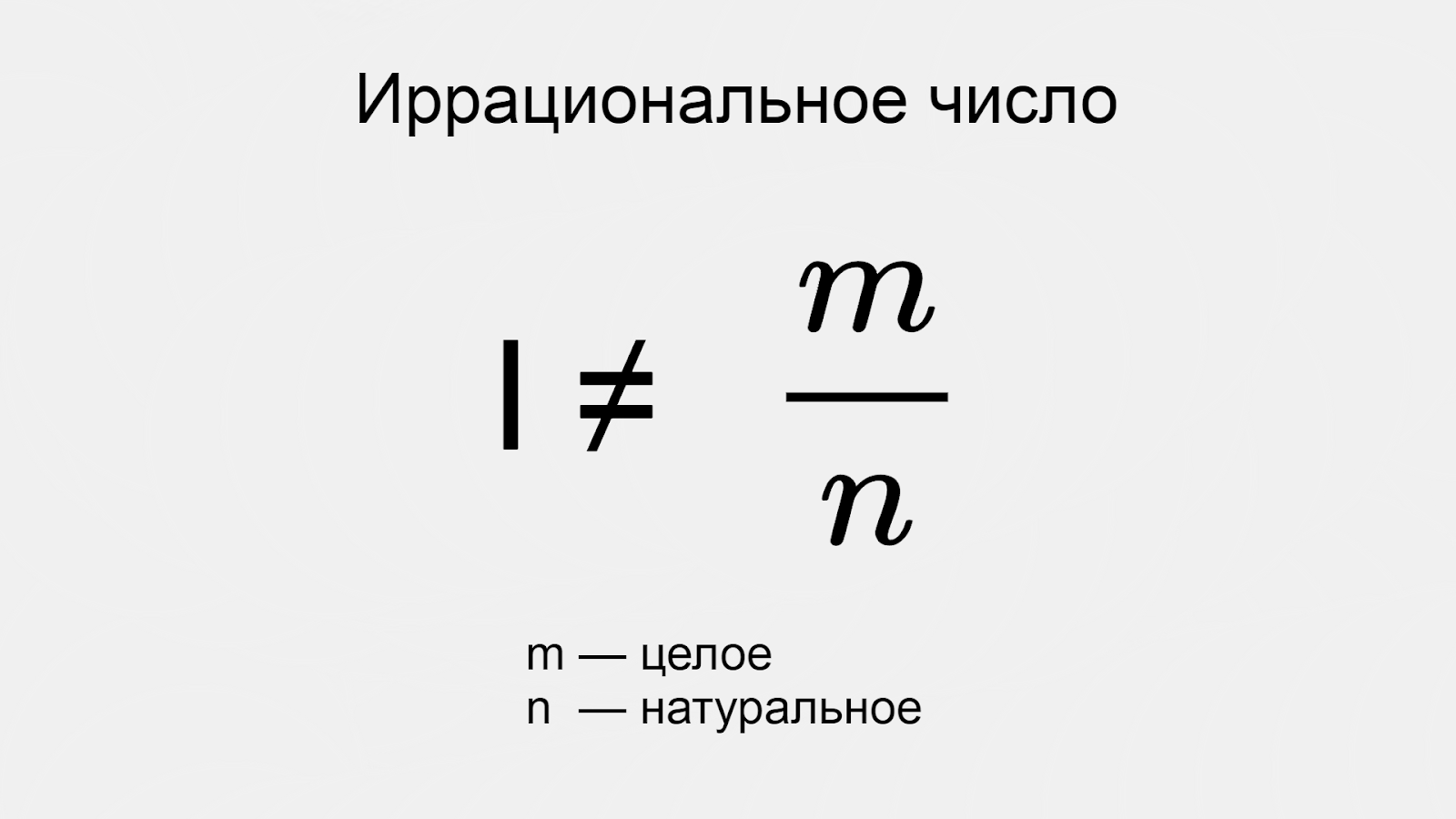
Простыми словами, иррациональное число — это бесконечная непериодическая дробь. «Бесконечная» означает, что у дроби есть бесконечное количество цифр после запятой. «Непериодическая» — что у этих цифр нет никакой повторяющейся закономерности.

Например, число √2 — иррациональное. Если попробовать извлечь из него корень с помощью калькулятора, получится число 1,4142135623… Цифры после запятой будут высчитываться бесконечно, а в их последовательности не будет никакой логики.

Другие примеры иррациональных чисел:

• Число Пи: π = 3,1415926535…
• Число Эйлера: e = 2,7182818284…
• Золотое сечение: φ = 1,6180339887…
• √2 = 1,4142135623…
• √3 = 1,7320508075…
• √5 = 2,2360679774…
• √7 = 2,6457513110…
• √11 = 3,3166247903…

Ещё один известный пример иррационального числа — число π (Пи). Учёные и по сей день соревнуются в попытках вычислить максимальное количество знаков после запятой у этого числа. Так, в 2022 году команда разработчиков из Google побила мировой рекорд, вычислив около 100 трлн знаков, в которых всё так же не находилось повторяющегося периода.

Так как иррациональные числа бесконечны, чисто гипотетически в нём рано или поздно можно встретить свой номер телефона, дату рождения или какую-либо закодированную информацию бесконечное количество раз.

Чем иррациональные числа отличаются от рациональных

Рациональные числа — это числа, которые можно представить в виде обыкновенной дроби — то есть деления двух целых чисел. Например, 0,5 можно записать как 5/10, а 6 — как 6/1.

Если в этих дробях разделить числитель на знаменатель, у нас получится ясный и предсказуемый результат — либо целое число, либо десятичная дробь. В крайнем случае, на выходе будет бесконечная периодическая дробь — такая, где есть повторяющееся значение после запятой.

Иррациональные числа устроены по-другому. Как бы вы ни старались, оно всегда будет принимать форму бесконечной непериодической дроби. Что-то вроде уже знакомого нам числа Пи: 3,1415926535… Поэтому их нельзя представить в виде дроби — просто нет двух чисел, которые при делении давали бы такого монстра :)

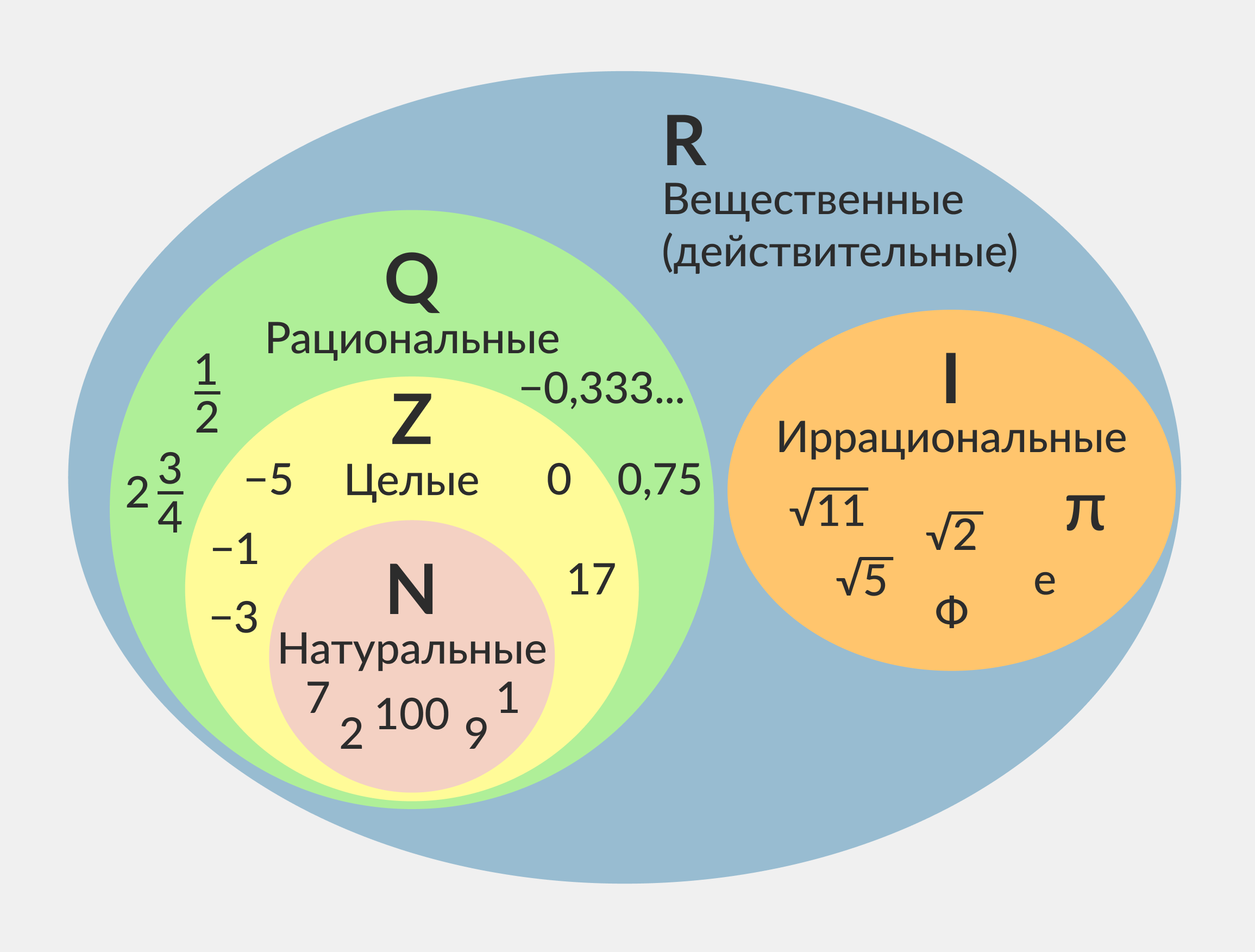
А вообще, оба вида чисел — иррациональные и рациональные — вместе образуют множество вещественных чисел. Это все числа, которые мы используем при повседневных расчётах. За пределами этого «пузыря» есть и другие числа — например, мнимые, но это уже тема для отдельной статьи.

Свойства иррациональных чисел

У иррациональных чисел, как и у любых других, есть свои свойства. Давайте пройдёмся по каждому из них.

1. Если сложить иррациональное число с рациональным, получится иррациональное число:

Это же правило действует и при вычитании:

2. Если умножить иррациональное число на рациональное, получится иррациональное число:

3. Если вычесть одно иррациональное число из другого, может получиться рациональное или иррациональное число:

4. При сложении или умножении двух иррациональных чисел может получиться рациональное или иррациональное число:

Иррациональные числа в геометрии

Иррациональное значение можно встретить, вычисляя длину гипотенузы единичного равностороннего треугольника. Это такой треугольник, где оба катета равны единице. Если мы попробуем вычислить гипотенузу такого треугольника, то получим иррациональное число — √2.

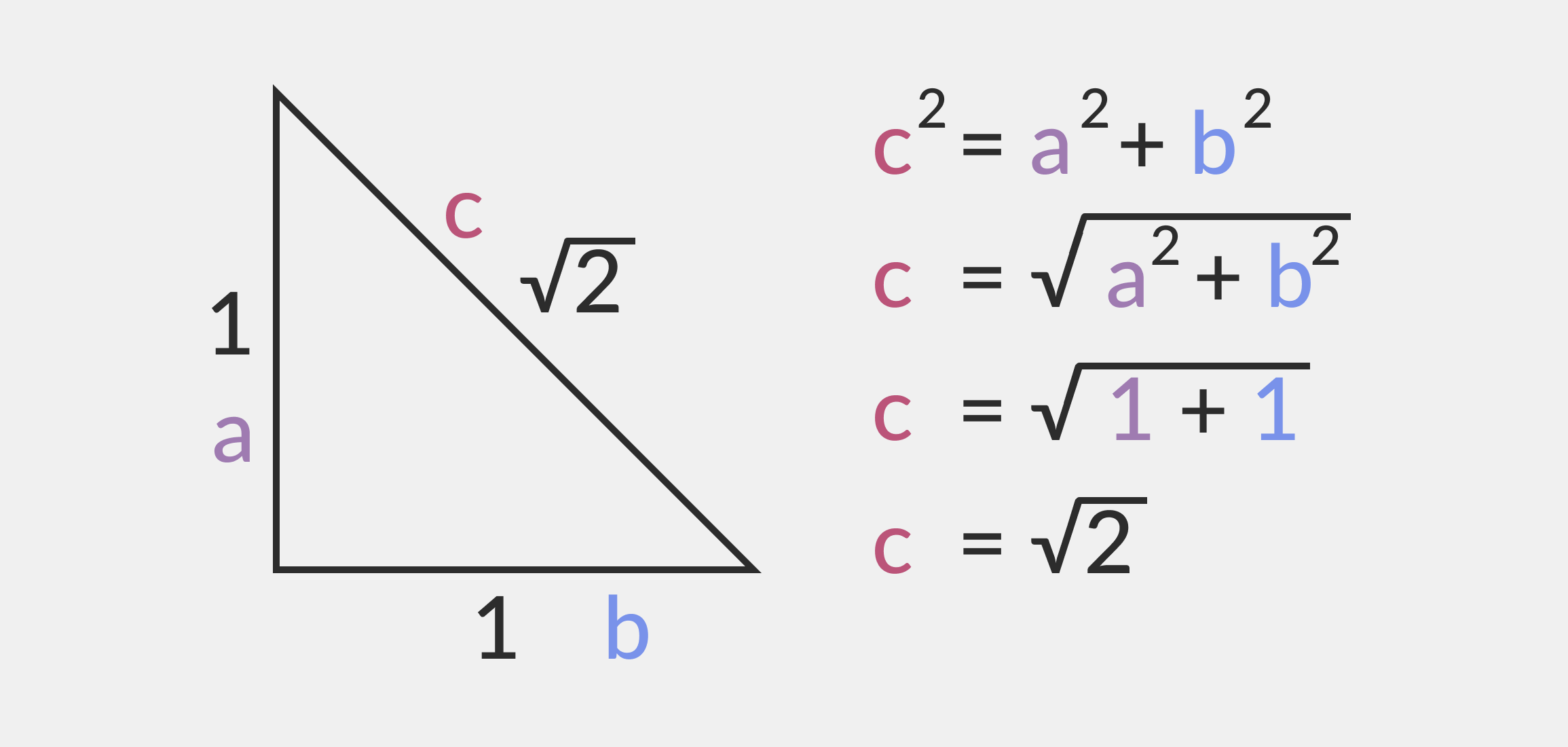
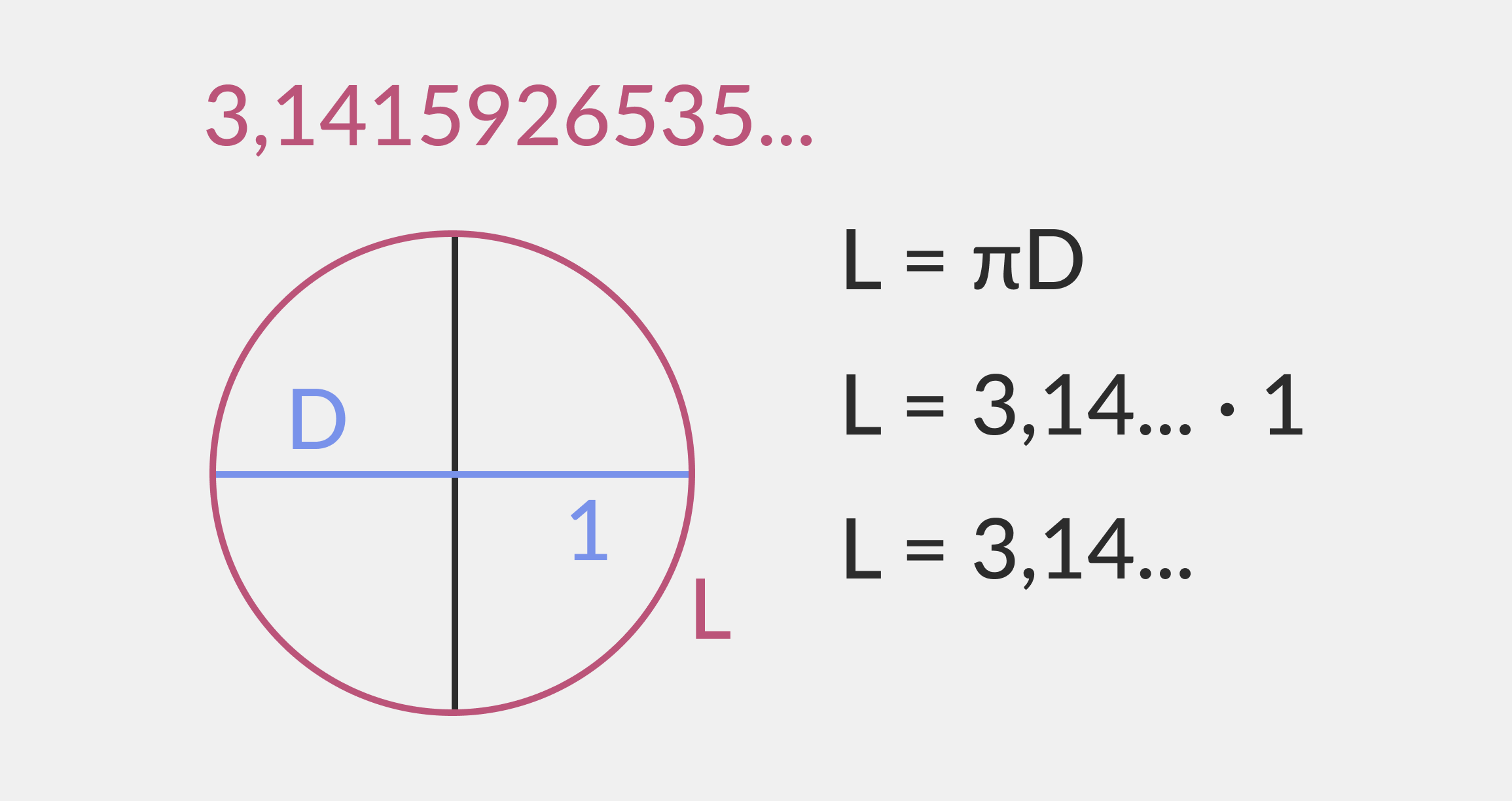
Другой пример — вычисление длины окружности, которое невозможно без иррационального числа π (Пи). Для этого диаметр окружности умножается на число Пи: L = πD = 2πr, где L — длина окружности, D — диаметр, r — радиус. Из этого можно сделать вывод, что число Пи — это длина окружности, разделённая на её диаметр.

Работаем с иррациональными числами в Python

Выведем некоторые иррациональные значения в консоль на языке Python. Для этого нам понадобится математический модуль math, для работы с константами и извлечением корня, а также модуль и класс Decimal, для более точного исчисления. Импортируем эти объекты для начала работы:

import math
import decimal
from decimal import Decimal

В модуле math уже имеются для работы три константы — число Пи, два Пи и число Эйлера. Вывести их на экран довольно просто:

# Число Пи
print(math.pi)
# Два Пи
print(math.tau)
# Число Эйлера
print(math.e)

3.141592653589793
6.283185307179586
2.718281828459045

Вы можете заметить, что количество знаков после запятой всего 15, хотя эти значения иррациональны. Это связано с тем, что тип данных переменных является float, и большее значение он хранить не может.

Попробуем извлечь квадратный корень из 2 с помощью функции sqrt () модуля math и специального оператора возведения в степень **:

print(math.sqrt(2))
print(2 ** 0.5)

1.4142135623730951
1.4142135623730951

Оба способа работают одинаково, но вывод ограничивается 16 знаками. Чтобы увеличить точность, воспользуемся классом Decimal. Для этого поместим объект в переменную x, зададим ему параметр prec (precision — точность), например 10000, и вызовем метод sqrt () для этой переменной:

x = Decimal(2)
decimal.getcontext().prec = 10000
print(x.sqrt()) # Извлечение корня

1.41421356237309504880168872420969807856967…// 10000 знаков

Мы получили 10 000 знаков после запятой при извлечении квадратного корня из 2. Таким же образом можно поиграться и с другими иррациональными значениями:

print(Decimal(3).sqrt())
print(Decimal(11).sqrt())
print(Decimal(17).sqrt())
print(Decimal(math.pi).sqrt())

1.732050807568877293527446341505872366942805253810380628…
3.316624790355399849114932736670686683927088545589353597…
4.123105625617660549821409855974077025147199225373620434…
1.772453850905515992751519103139248439290428205003682302…

И напоследок вычислим иррациональное число Пи, используя характеристики нашей планеты. Длина окружности Земли составляет примерно 40 075,017 километров, а её диаметр — 12 756 километров. Зная формулу длины окружности L = πD, можно легко выйти на таинственное число Пи — π = L/D:

# Длина окружности Земли
L = Decimal(40075.017)
# Диаметр Земли
D = Decimal(12756)
# Вычисляем число Пи
pi = L / D
print(pi)

3.141660159924741284523127724960628592059619002822201317…

У нас получилось примерное число Пи, где точность после запятой совпала на три знака, потому что изначальные данные лишь приблизительные. Но в целом получились всё то же иррациональное число с бесконечным периодом.

Коротко о главном

Из этой статьи мы узнали, что такое иррациональные числа, какие у них есть свойства, и даже увидели кусочек бесконечного хаоса в консоли на Python :)

Повторим основные моменты:

• Иррациональные числа — это бесконечные десятичные дроби с неповторяющимся значением после запятой.
• Этим они отличаются от рациональных чисел, которые тоже могут быть бесконечными дробями, но всегда содержат повторяющийся период после запятой.
• При этом оба вида чисел относятся к одному и тому же множеству вещественных чисел.
• Самый известный представитель иррационального множества — число Пи (π = 3,141592…). Чаще всего оно используется в геометрии для нахождения длины окружности.
• К иррациональным числам применимы все математические операции: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.