Готовимся к собеседованию: случайные числа в Python
Случайность управляет миром, а вы будете управлять случайностью. С помощью Python, конечно.


Чтобы имитировать бросок кубика в игре или предсказать загруженность интернет-ресурса, нужны случайные числа.
Мы разобрали самые популярные вопросы о случайных числах в Python с собеседований. Чаще всего для ответа достаточно написать код и кратко его прокомментировать. Да пребудет с вами Великий Рандом!
Главное, что нужно помнить
- Случайные числа — это последовательность чисел, которая подчиняется одному из законов распределения.
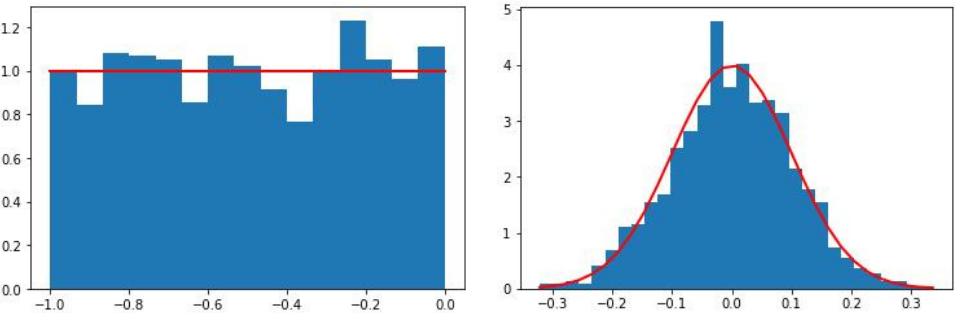
- Главных распределений два: равномерное, с графиком в виде горизонтальной линии, и нормальное, с графиком-колоколом (его ещё называют гауссианой).
- Основная Python-библиотека для генерации случайных чисел называется random.
- Большинство случайных чисел в программировании — не случайные, а псевдослучайные.
Вопрос 1. Что такое случайные числа?
Сложность: 1/3
Что нужно помнить: случайные числа — это математическое понятие, и их не следует путать с обыденными, произвольными числами. Случайное число в математике и программировании — это:
- число из определённого диапазона,
- у которого есть определённая вероятность выпадения.
Другими словами, существует закон или правило, которое называется «функцией распределения» или просто «распределением». И это самое распределение «раздаёт» каждому числу из диапазона определённую вероятность выпадения.
В качестве диапазона значений математикам и программистам привычнее всего использовать диапазон действительных чисел от 0 до 1, но это могут быть и целые числа от 1 до 6, как в игральном кубике, или от 100 до 1 000 000 — и так далее. Главное, что и распределение, и диапазон известны заранее, а само число нет.
Итого: случайные числа — это искусственно полученная последовательность чисел из определённого диапазона, которая подчиняется одному из законов распределения случайной величины.
Распределения бывают разные. Так, равномерное распределение — это когда любое значение из диапазона имеет одну и ту же вероятность выпадения (как у игрального кубика или монетки). Если же распределение, например, нормальное (гауссиана), то чаще выпадают числа из середины диапазона. Есть даже таблица — она поможет выбрать подходящее распределение.
Вопрос 2. Как получить случайные числа в Python?
Сложность: 1/3
Основных способов два: с помощью «родной» библиотеки random и с помощью модуля numpy.random из библиотеки numpy.
Прежде чем интервьюер придерётся, не забудьте сказать, что и random, и numpy.random — генераторы псевдослучайных чисел (о них ниже). Истинно случайные числа можно получить, например, c сайта Random.Org: там они генерируются с помощью атмосферного шума.
import random
# Случайное число между 0 и 1 (исключая 1)
random.random()
# Случайное число между 1 и 2, равномерное распределение
random.uniform(1,2)
# Случайное число, нормальное распределение
# 1 и 2 здесь уже не границы диапазона, а параметры mu и sygma
random.gauss(1,2)
Библиотека random имеет меньший объём, чем numpy.random, и проще в использовании. Зато numpy.random содержит дополнительные распределения для научных вычислений, а также функции для генерирования целых массивов случайных данных.
from numpy.random import default_rng
rng = default_rng()
vals = rng.standard_normal(10)
В первой строчке мы импортировали default_rng — это «генератор генераторов» случайных массивов из модуля numpy.random. Во второй — создали экземпляр такого генератора и присвоили ему имя rng. В третьей использовали его метод standard_normal, чтобы получить numpy-массив из 10 случайных чисел, и записали массив в переменную vals.
Вопрос 3. Псевдослучайные числа
Сложность: 3/3
Псевдослучайные числа — это, если очень упрощать, последовательность чисел, которая только выглядит случайной, а на самом деле каждое число в ней определяется алгоритмом, то есть вычисляется. Псевдослучайные последовательности цикличны: через какой-то период все числа повторяются в точности в том же порядке.
Библиотека random и модуль numpy.random содержат в себе генератор не истинно случайных, а именно псевдослучайных чисел.
Генерировать истинно случайные числа дорого и сложно. Основная трудность состоит в том, чтобы гарантировать отсутствие какого-либо цикла, правила или алгоритма. Чаще всего истинно случайные числа берут из физического мира: шумов атмосферы, детекторов частиц, колебаний электрического тока или из космического излучения.
То, что псевдослучайная последовательность, в отличие от истинно случайной, воспроизводима, очень удобно для практических задач: часто нужно подать на вход ту же самую последовательность второй раз, чтобы посмотреть, как работает программа после добавления новых фич.
Наиболее популярный современный алгоритм генерирования псевдослучайных чисел разработан в 1997 году и носит красивое название «Вихрь Мерсенна». Он используется и в Python. Последовательность чисел, порождённая им, статистически неотличима от истинно случайной и имеет период, равный числу с шестью тысячами знаков. Этого хватает для задач симуляции и моделирования, но с точки зрения криптографии такая последовательность всё равно небезопасна: для успешной атаки достаточно иметь сравнительно небольшую сгенерированную этим генератором последовательность.
Вопрос 4. Как повторить случайную последовательность?
Сложность: 2/3
Истинно случайную последовательность повторить невозможно. Но для повторения псевдослучайных чисел в обеих основных библиотеках — random и numpy.random есть функция seed (), которая отвечает за инициализацию («посев») последовательности.
import random
random.seed(42)
print(random.random()) # 0.6394267984578837
print(random.random()) # 0.025010755222666936
random.seed(42)
print(random.random()) # 0.6394267984578837
Передавая аргумент 42 в функцию seed (), мы указываем конкретное место в псевдослучайной последовательности, поэтому команда random.random () в третьей и последней строках выдаёт одинаковое число — оно идёт первым после точки, помеченной как seed (42).
В seed () можно передать целые и дробные числа, а также строки и кортежи. Если оставить скобки пустыми, то в качестве аргумента seed () возьмёт текущее системное время.
Аналогичная функция есть в модуле numpy.random:
import numpy as np
np.random.seed(42)
print(np.random.rand()) # 0.3745401188473625
print(np.random.rand()) # 0.9507143064099162
np.random.seed(42)
print(np.random.rand()) # 0.3745401188473625Вопрос 5. Красные и зелёные шары
Сложность: 1/3
Часто на собеседованиях просят написать программу, связанную с вероятностями. Например, код для численной проверки ответа к задачке «Какова вероятность вытащить зелёный шар из мешка, в котором 1 зелёный и 4 красных шара».
(Ответ ⅕ = 0,2).
Иными словами, если 100 раз вынимать шар из мешка, возвращая его обратно, количество выпадения зелёных шаров должно приближаться к 20. Вариант кода для проверки:
import random
green_ball_count = 0 # счётчик зелёных шаров
for i in range(0,100):
new_ball = random.choice(['green', 'red', 'red', 'red', 'red'])
if new_ball == 'green':
green_ball_count = green_ball_count + 1
print (green_ball_count)Функция random.choice () случайным образом выбирает значение из заданного диапазона — списка из одного «green» и четырёх «red». Код выведет количество зелёных шаров после 100 попыток.
Вопрос 6. Нечестная монетка
Сложность: 1/3
Другой вариант: предположим, у нас есть так называемая «нечестная» монетка, где орёл (H, «heads») и решка (T, «tails») выпадают не с вероятностью ½, как положено, а по-другому: орёл с вероятностью p (H) = 0,2, а решка, соответственно, p (T) = 0,8.
Тогда код для проверки будет выглядеть примерно так:
import random
H_count = 0
for i in range(0,10000):
new_flip = random.choices(['H', 'T'], weights=[0.2, 0.8])
if new_flip == ['H']: # внимание: функция choices возвращает список!
H_count = H_count + 1
print (H_count)Здесь используется другая функция, choices, в которую вместе со списком значений можно в параметре weights передавать вероятности их выпадения.
Код выведет количество выпавших орлов после 10 000 бросков.
К слову: задачи на нечестные монетки, наряду с поиском n-ного числа Фибоначчи и нахождением угла между часовой и минутной стрелками, кочуют из одного собеседования в другое уже не первый десяток лет. Есть вероятность, что одна из них попадётся и вам.
Вопрос 7. Проиллюстрируйте закон больших чисел
Сложность: 2/3
Закон больших чисел (ЗБЧ) говорит, что при увеличении количества попыток случайная величина стремится к своему математическому ожиданию — всё усредняется. Подробнее об этом можно прочитать в нашей статье об основах математики для Data Science.
Код для иллюстрации ЗБЧ на примере честной монетки выглядит так:
import random
import matplotlib.pyplot as plt
total_flips = 0
numerical_probability = []
H_count = 0
for i in range(0,5000):
new_flip = random.choices(['H', 'T'], weights=[0.5, 0.5])
total_flips = total_flips + 1
if new_flip == ['H']: # внимание: функция choices возвращает список, а не строку ‘H’ или ‘T’!
H_count = H_count + 1
numerical_probability.append(H_count/total_flips)
# рисуем график
plt.plot(numerical_probability)
plt.xlabel("Количество бросков")
plt.ylabel("Численная вероятность")Вначале мы импортировали уже знакомый нам модуль random и модуль matplotlib.plt — он нужен для рисования простых графиков. После этого определили переменные: общее количество бросков (total_flips), список из значений вероятностей (numerical_probability), количество выпавших орлов (H_count).
Теперь в цикле мы 5 000 раз «подбрасываем» монетку. Если выпадает орёл («H»), то делим текущее количество выпавших орлов на текущее количество бросков и добавляем итоговое значение в конец списка numerical_probability. В конце рисуем график.
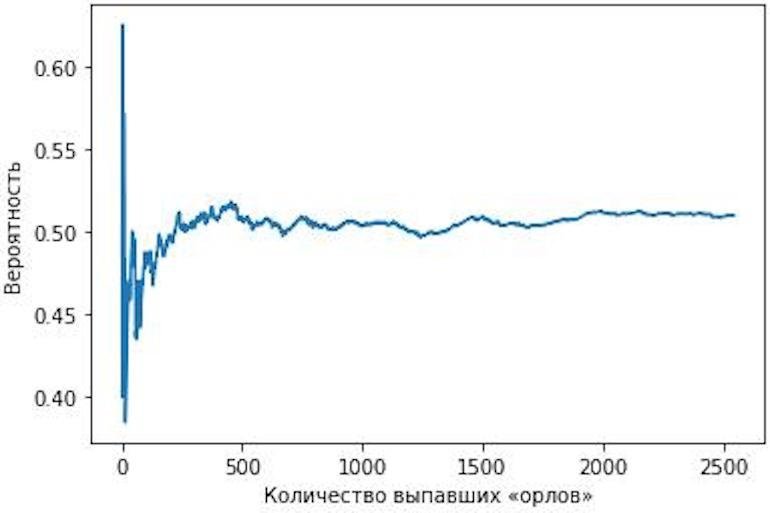
Чем больше бросков, тем ближе к 0,5 вероятность выпадения орла. Всё, как и предсказывает закон больших чисел.
Вопрос 8. Где применяются случайные числа?
Сложность: 2/3
В логистике: при расчётах страховых запасов товара — чтобы склад внезапно не опустел или, наоборот, не пришлось держать избыток товара слишком долго. Принято считать, что поведение покупателей случайно и подчиняется одной из разновидностей нормального распределения. В особо запущенных случаях считается случайным даже поведение поставщиков.
В науке: с помощью метода Монте-Карло учёные моделируют поведение частиц во фрактальном окружении в трёхмерном пространстве. Метод Монте-Карло основан на использовании большого количества генерируемых случайных чисел.
В микроэлектронике: броуновское движение частиц играет важную роль в формировании пористости плёночного покрытия полупроводников при напылении его на поверхность. Просчитать это на компьютере гораздо дешевле, чем экспериментировать с реальным покрытием, поэтому сначала его рассчитывают, а потом запускают в производство.
В криптографии: для генерации шифровальных ключей. Здесь становится особенно важным различие между псевдослучайными и истинно случайными числами.
Случайности не случайны
Так говорил мастер Угвэй, и мы теперь понимаем его чуть лучше: он жил довольно долго, мог заметить период повторения одних и тех же событий и догадаться, что все случайности в этом мире на самом деле псевдослучайны. У нас с вами времени меньше, поэтому придётся изучать документацию: random, numpy.random.










