Фракталы: что это такое и какие они бывают
Начнём с того, что это не только красивые психоделические картинки, но и универсальный способ описать геометрию живой природы.


Есть в математике вещи, настолько завораживающие своей красотой, что на них можно смотреть вечно. Одно из таких чудес — фракталы. Это фигуры, которые рекурсивно воспроизводят сами себя, создавая причудливые узоры в двух- и трёхмерном пространствах. Но дело не только в узорах: за этими картинками кроется целый подход к исчислениям и описанию живого мира.
Содержание
Что такое фрактал
Фрактал — это фигура, обладающая свойством самоподобия. Объект называют самоподобным, если одна или более его частей похожа на его целое. При этом количество повторяющихся частей у фрактала стремится к бесконечности — этим он отличается от самоподобных геометрических фигур с конечным числом звеньев (предфракталов).

Изображение: Лев Сергеев для Skillbox Media
Термин «фрактал» ввёл в 1975 году американский математик Бенуа Мандельброт. За основу он взял латинское слово fractus, означающее «разделённый на части». Позже Мандельброт выпустил книгу «Фрактальная геометрия природы» (The Fractal Geometry of Nature), в которой представил новый метод описания сложных природных объектов на основе фракталов. Обычные, или евклидовы, фигуры с этой задачей не справлялись, ведь в природе не существует прямых линий, треугольников, квадратов кругов и так далее.
Однако о концепции фракталов было известно задолго до первых работ Мандельброта. Первую такую фигуру, которая вошла в историю как «множество Кантора» (позже мы расскажем про неё подробнее), открыл Георг Кантор в 1883 году. На её основе математик продемонстрировал и самоподобие, и рекурсию.
Позже учёные обнаружили рекурсию в объектах живой природы: деревьях, молниях, облаках и других. Оказалось, что структура таких объектов подобна структуре их частей, а значит, их можно описать неким математическим законом и не пытаться изобразить квадратами, кругами и другими классическими геометрическими фигурами.

Читайте также:
Сегодня модели на основе фракталов применяются в физике, биологии, медицине и других науках. А учёные продолжают находить закономерности, связанные с ними, в самых разных явлениях нашей Вселенной.
Виды фракталов
Фракталы принято делить на геометрические, алгебраические и стохастические.
Геометрические — строятся на основе исходной фигуры, которая определённым образом делится и преобразуется на каждой итерации.
Алгебраические — строятся на основе алгебраических формул.
Стохастические — образуются в том случае, если в итерационной системе случайным образом изменяется один или несколько параметров.
Далее мы подробно разберём каждый класс.
Геометрические фракталы
Эти фигуры основаны на прямых линиях, квадратах, кругах, многоугольниках и многогранниках. Рассмотрим несколько примеров от самого простого к сложному.
Множество Кантора
В 1883 году Георг Кантор — немецкий математик, автор теории множеств — придумал множество, которое повторяло само себя снова и снова. Кантор взял произвольный отрезок и разделил его на две части, потом каждую — ещё на две и так далее:

Каждый этап деления прямых на две части называется итерацией.
Итерация — это повторение одного и того же действия, или, по аналогии с программированием, одно прохождение тела цикла. На первой итерации у нас был один отрезок, на второй мы получили два, на третьей — четыре и так далее. Если повторять это несложное действие бесконечное количество раз и увеличить масштаб изображения, то мы увидим ту же самую картину, что и в самом начале. Это и есть визуальное воплощение самоподобия:
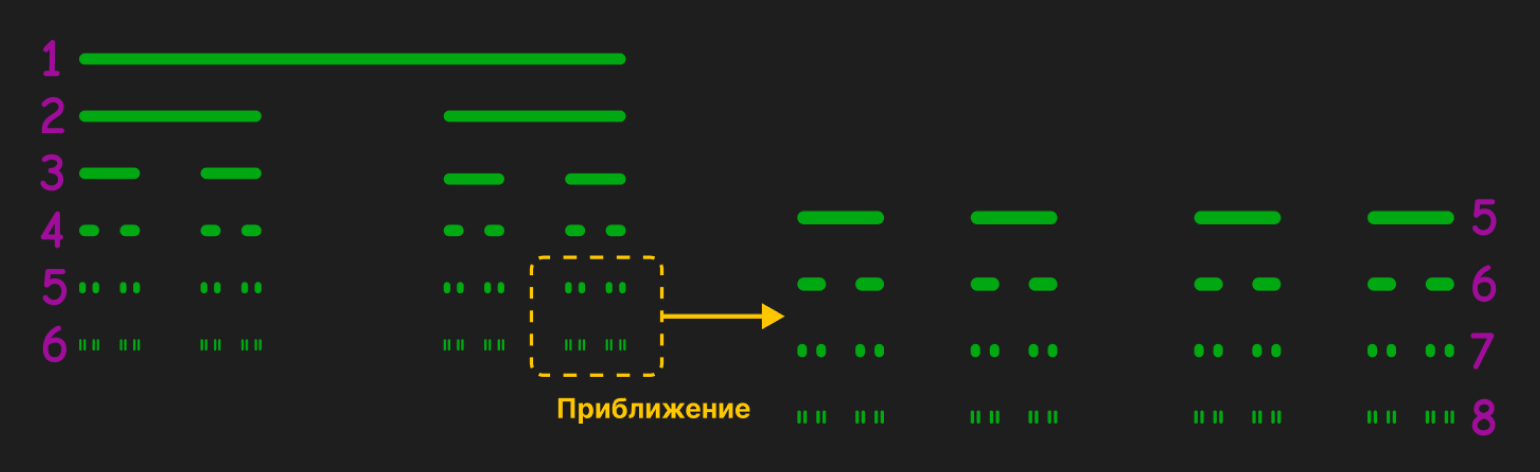
Снежинка Коха aka кривая Коха

Шведский математик Хельге Фон Кох в 1904 году описал кривую, воспользовавшись треугольником и методом самоподобия, в результате чего получилась фрактальная снежинка.
Ниже показаны четыре итерации построения такой фигуры. Слева изображены исходные кривые, а справа — получившаяся из этих кривых снежинка. Нетрудно заметить, что в снежинки идеально вписывается как равносторонний треугольник, так и сама кривая:

На какой бы итерации мы ни увеличили масштаб изображения, мы всегда сможем увидеть знакомый паттерн, как и с множеством Кантора. Посчитать периметр такой снежинки невозможно, потому что она может разрастаться всё дальше и дальше… Это ещё одно свойство фракталов — бесконечность.
Ковёр, треугольник и кривая Серпинского

Польский математик Вацлав Серпинский брал за основу фрактала не только кривую, но и квадрат с треугольником.
Для начала рассмотрим, как «размножается» кривая Серпинского. При каждой итерации количество её копий увеличивается в четыре раза, а рисунок становится сложнее:

Треугольник же на каждом шаге дробится на три равные части:

Квадрат, или ковёр, Серпинского получается так же, как и треугольник, но исходная фигура делится на восемь квадратов. Уже на пятой итерации становится тяжело разглядеть отдельные квадраты:

Губка Менгера

Как уже говорилось ранее: геометрические фракталы могут строиться на основе многогранников, то есть быть объёмными.
Ковёр Серпинского в трёхмерном пространстве превратится в кубический многогранник. Такой фрактал называют губкой Менгера:

Если бы мы влетели внутрь такого фрактала и попытались приблизиться к любой из сторон, то заблудились бы и никогда из него не выбрались, потому что внутри губки Менгера скрыто бесконечное пространство! По такому же принципу можно смоделировать и трёхмерный треугольник Серпинского.
Дерево Пифагора

Следующую рекурсивную фигуру построил математик Альберт Босман в 1942 году. В её основе лежит знаменитая теорема Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы. Полученный геометрический фрактал напоминает дерево, поэтому его и назвали деревом Пифагора.
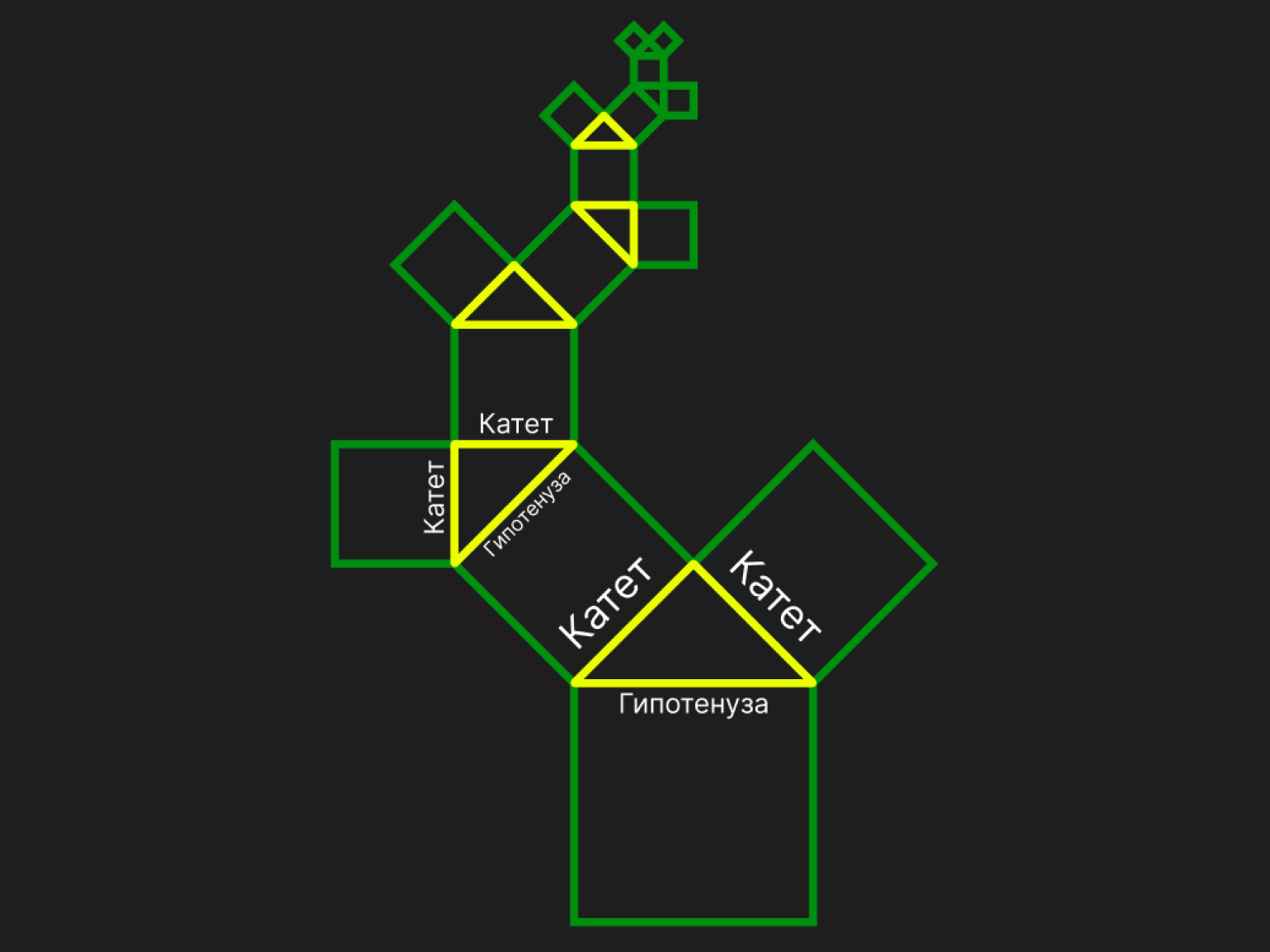
Знакомым с алгоритмами читателям дерево Пифагора может напомнить другое, бинарное дерево. В целом, бинарный поиск напоминает принцип Кантора, где на каждой итерации получается вдвое больше разветвлений (отрезков). Всё это — ещё одна иллюстрация самоподобия, о котором мы говорили ранее.
Алгебраические фракталы
Алгебраические фракталы, в отличие от геометрических, основываются на формуле, а не на фигурах, но также рекурсивно итерируются. Выглядят они ещё более причудливо, чем те, что мы рассмотрели выше.
Множество Мандельброта
В 1905 году французский математик Пьер Фату описал множество, которое в 1970-х было впервые смоделировано Бенуа Мандельбротом (с ним мы уже знакомы) с помощью компьютера на комплексной плоскости:

В основе такого множества лежит формула:
Zn+1 = Zn² + C,
где Z и C — комплексные числа.
Остановимся на комплексных числах. Вы наверняка знаете, что извлекать квадратный корень из отрицательных чисел нельзя — это следует из того, что любое отрицательное число в квадрате является положительным.
Логика железная и справедливая, но лишь для действительных чисел. Если не переходить на строгий математический язык, то к действительным относят все целые и дробные числа (в том числе периодические), которыми мы пользуемся в повседневных расчётах: 1, 0, -56,7, 1/3, 5/6, и так далее.
Помимо действительных, в математике есть ещё большее множество комплексных чисел, которые имеют следующий вид:
a + bi,
где a и b — это вещественные числа,
а i — мнимая единица, равная √-1.
Вот здесь-то и ломается привычная арифметика.
«Что за ересь?! Нас ведь с пятого класса учили, что из отрицательных чисел квадратный корень не извлечь», — скажете вы и будете правы! Да, такая запись на первый взгляд кажется парадоксальной, и многие математики на первых порах с подозрением относились к подобной «магии». Но именно она в XVI веке помогла решить некоторые проблемные кубические уравнения. А потом комплексные числа нашли применение и в других областях, например в тригонометрии.
Возвращаемся к нашему Мандельброту. Небольшая шпаргалка, чтобы напомнить, о чём шла речь:
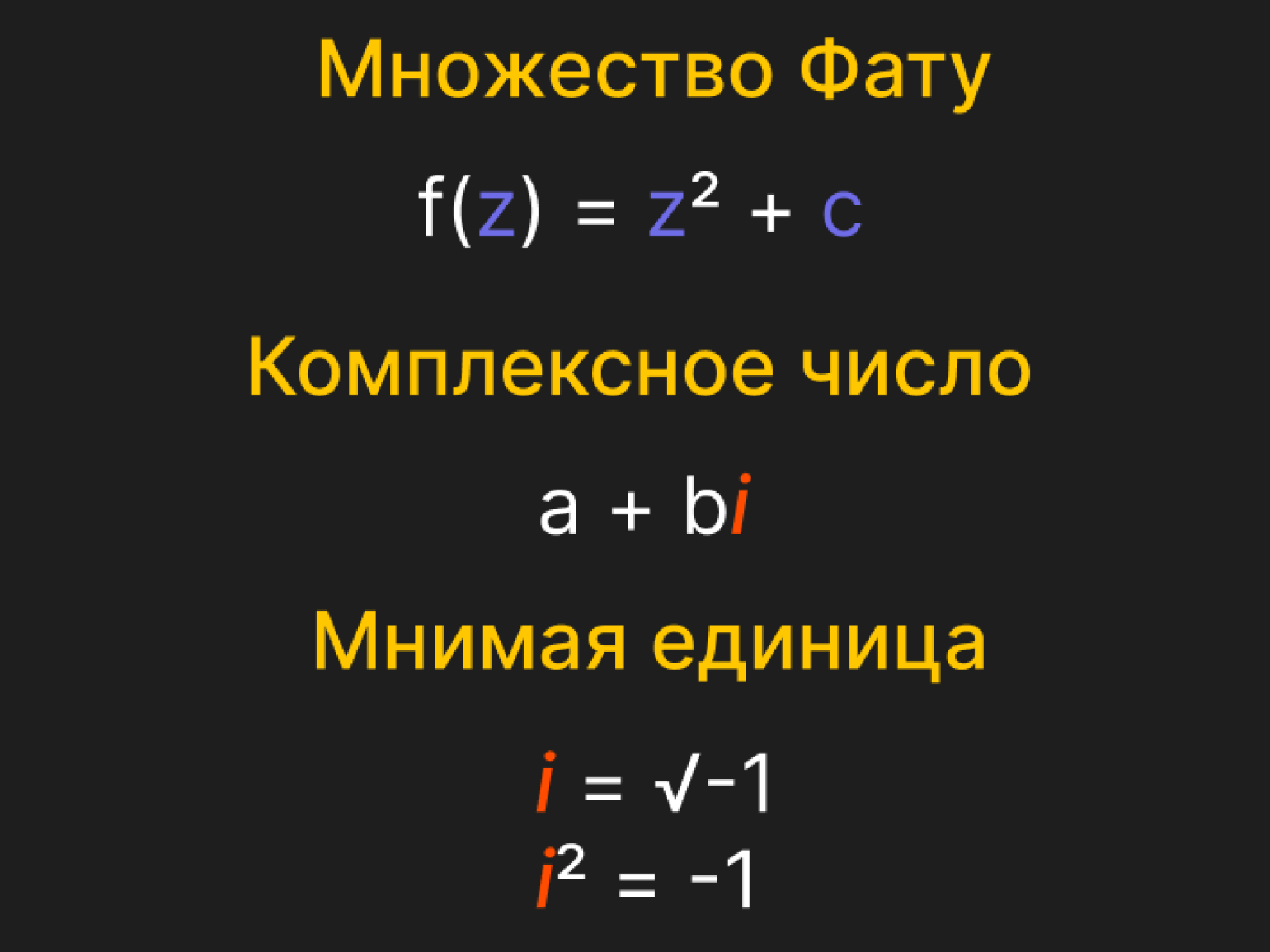
Суть фрактала Мандельброта та же, что и у предыдущих: на каждой новой итерации мы используем значение функции из предыдущего шага. В результате получаются невероятные картины!
Приближаясь к любым координатам множества Мандельброта, вы увидите всё новые и новые бесконечные узоры, которые напоминают изначальный вариант. Рассматривать и изучать такие фракталы можно бесконечно.
Ниже пример, на котором мы приблизились всего лишь к одной точке фрактала Мандельброта:
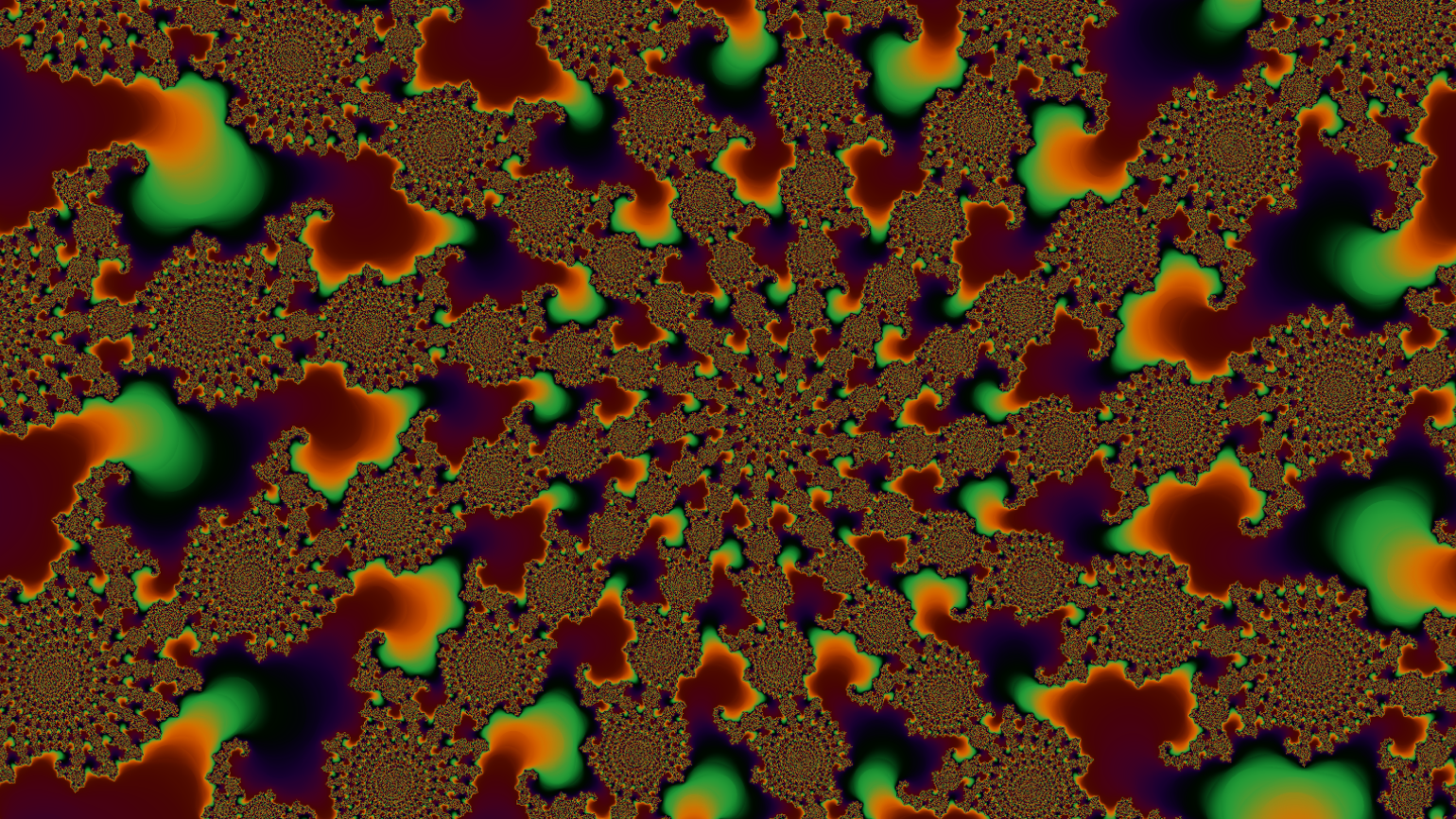
Множество Жюлиа
Множество, созданное французом Гастоном Жюлиа, также основывается на формуле Фату f (z) = z² + c и напоминает фрактал Мандельброта, но имеет некоторое математическое отличие, что влияет на конечный результат:

Если не углубляться в математические тонкости, можно сказать, что множество Мандельброта на каждой итерации использует новое значение параметра C, а Жюлиа оставил это значение на каждом новом цикле фиксированным. Поэтому при разных значениях C, фрактал Жюлиа можно визуализировать по разному, например так:

Стохастические фракталы
Если в геометрических и алгебраических фракталах формула постоянна, то в стохастических она меняется — и не один раз. Изменение может проходить как по конкретному закону, так и произвольно, но в обоих случаях это приводит к фантастическому визуальному эффекту!
Следующее изображение основано на нескольких фрактальных формулах:

С помощью сложных стохастических законов учёные могут воспроизводить структуры объектов живой природы. Добавляя отклонения на различных итерациях к таким фракталам, как дерево Пифагора, или снежинка Коха, мы можем получить изображение наклонившейся листвы или сгенерировать сколько угодно неповторимых снежинок.
Фрактальная графика
На принципе самоподобия основано целое направление в компьютерной графике. При таком подходе компьютер хранит не готовый объект, а лишь формулу его отрисовки, что значительно экономит память.
Таким образом, появляется возможность рисовать конкретные объекты и абстрактные 3D-модели, описывая лишь часть итогового изображения. Например, можно сгенерировать известный папоротник Барнсли, указав формулу для построения одной ветви, количество итераций и добавив хаотичные изменения на последующих итерациях:
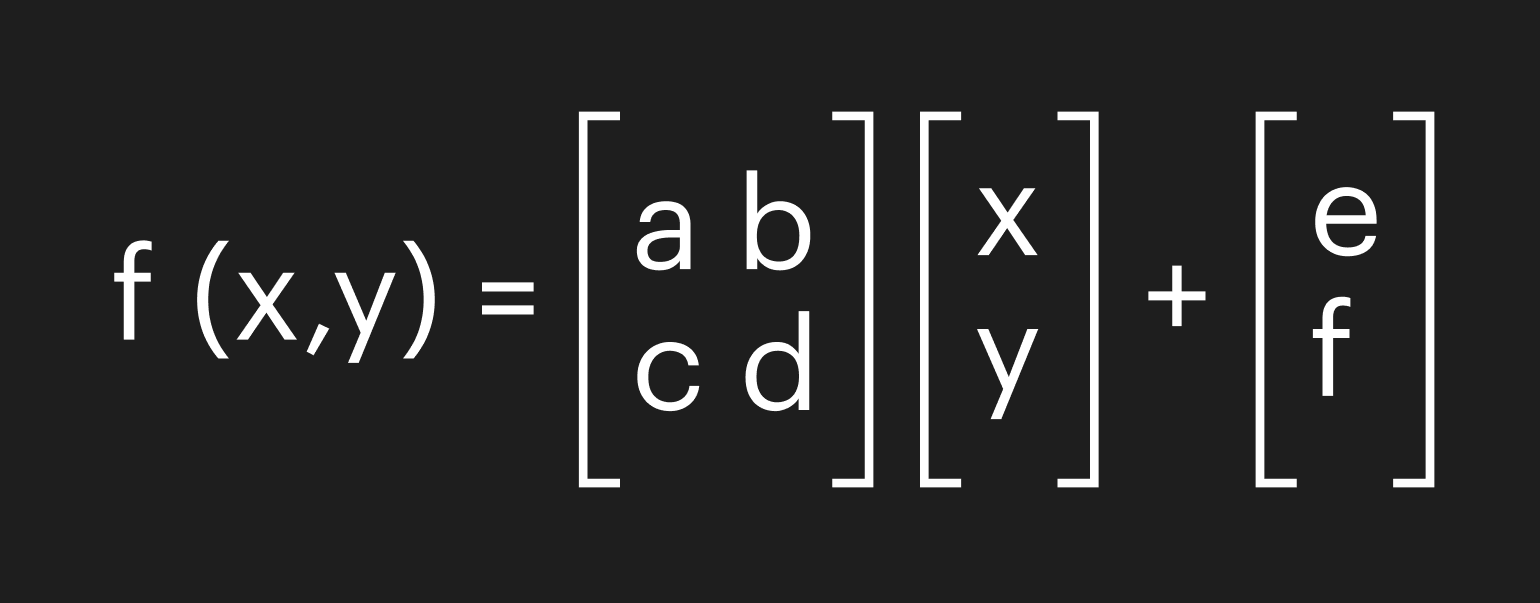
Изображение: Лев Сергеев для Skillbox Media
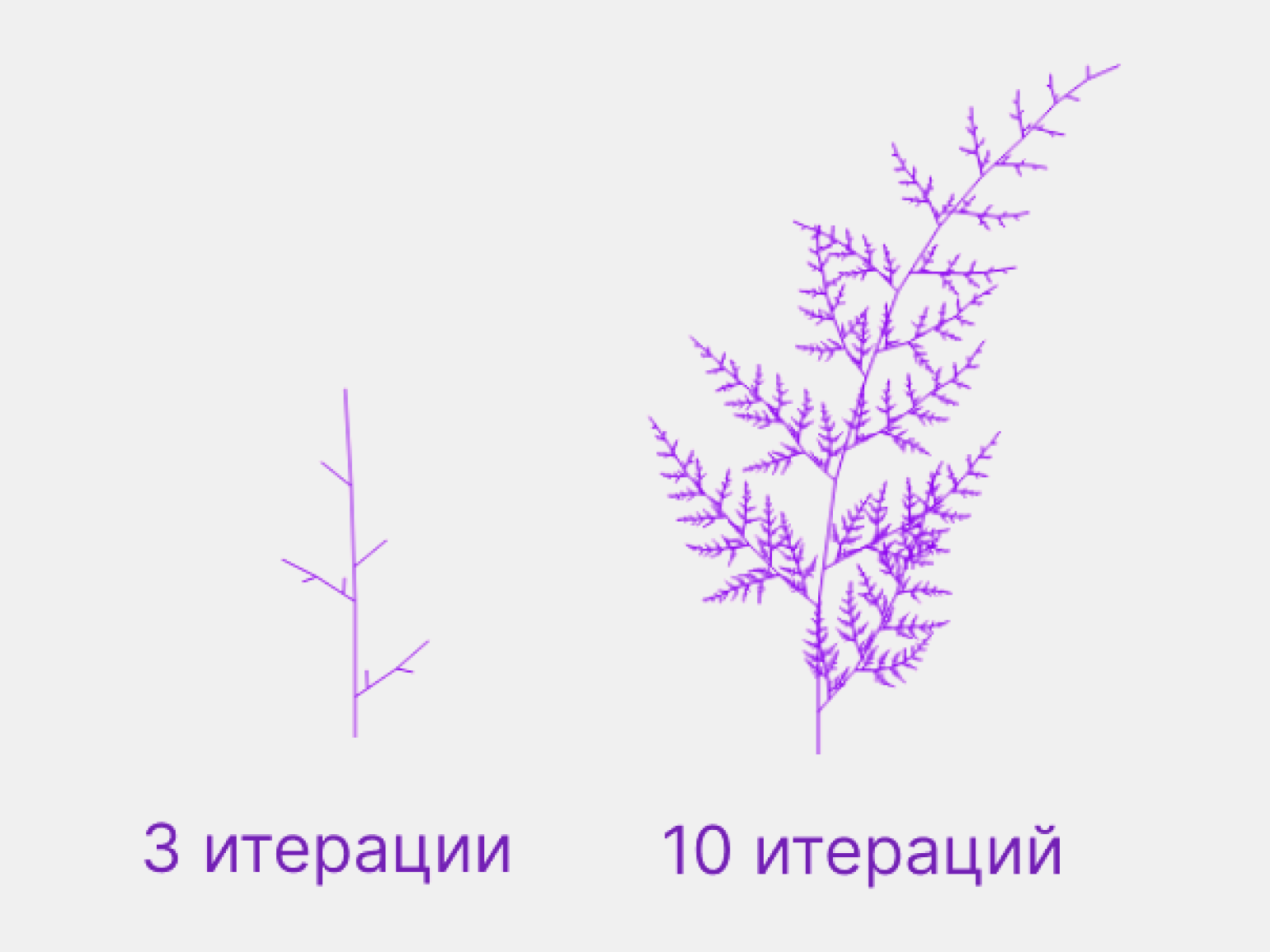
Изображение: Лев Сергеев для Skillbox Media
Фракталы в физике
Принципы построения фракталов используются в физике, в таких разделах, как гидродинамика, физика плазмы, электродинамика и радиоэлектроника. Одно из самых заметных изобретений в этой области — фрактальная антенна, которая была разработана американским инженером Натаном Коэном в 1995 году.
Главное преимущество такой антенны заключается в её широком диапазоне рабочих частот. А ещё она занимает намного меньший размер, чем аналоги классической формы, и может выступать в качестве основы для подводных антенн.
Конструкция Коэна напоминает снежинку Коха:
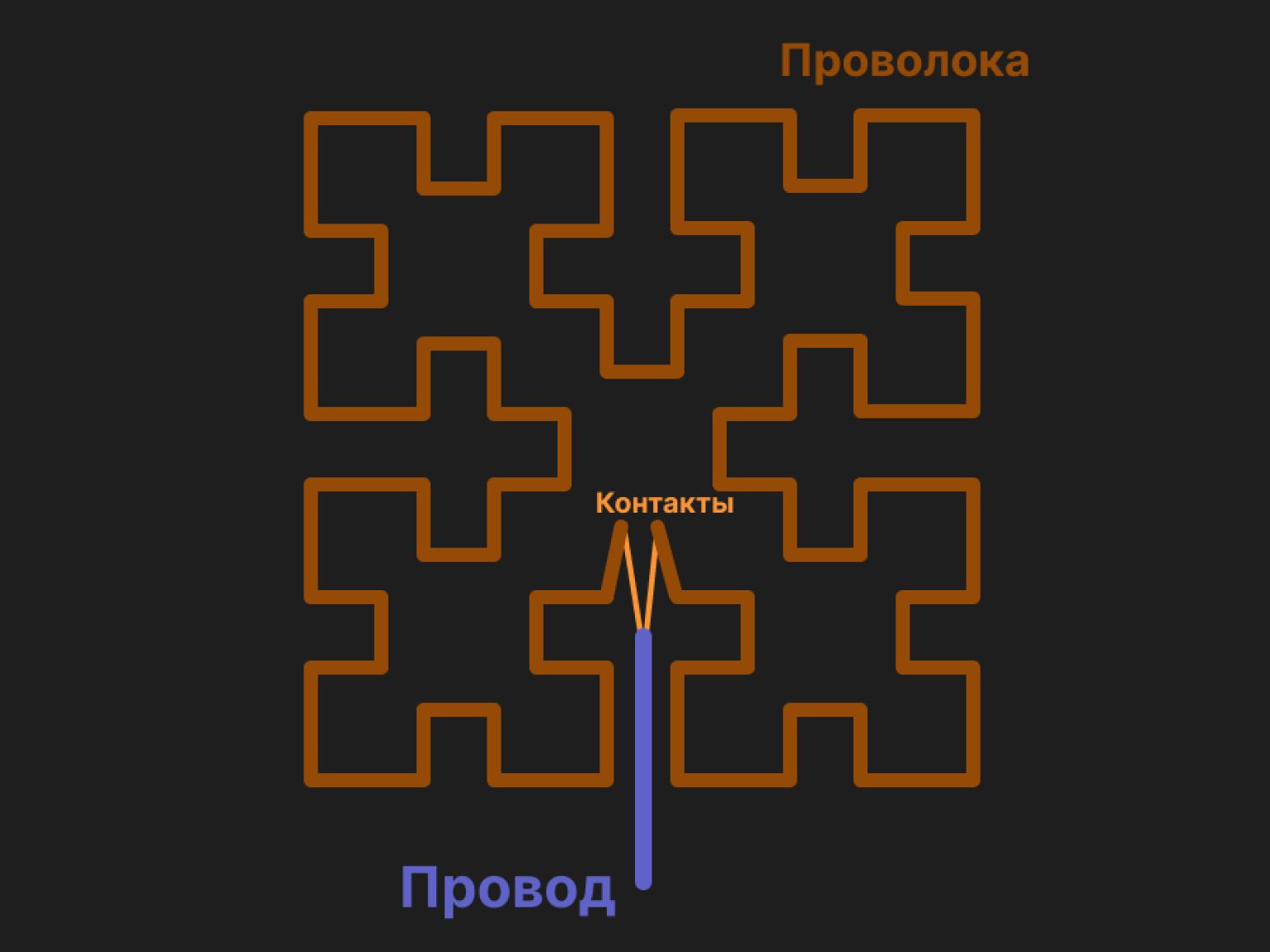
В 2000-х подобные антенны размером 30 × 40 мм стали использовать в мобильных устройствах. А чуть позже инженеры научились строить антенны на основе фракталов Серпинского, кривых Пеано и того же фрактала Коха.
Фракталы в природе
Как уже было сказано ранее, стохастические фракталы подарили науке новый подход к описанию природных объектов и явлений. А всё потому, что горы, облака, молнии, реки, растения, клетки живых организмов и даже галактики обладают общим свойством самоподобия.
Вот, например, один из самых красивых фракталов в природе — капуста Романеско:

Фото: Reissaamme / Pixabay.com
В реальной жизни фракталы встречаются практически на каждом шагу — достаточно выйти во двор оглядеться вокруг. Скажем, дерево Пифагора неслучайно получило своё название, ведь ветви деревьев ярче всего демонстрируют принцип самоподобия:

Вот ещё несколько примеров стохастических фракталов в листьях и растениях:

Вместо вывода: применение фракталов в жизни
Сегодня фракталы широко используются в самых разных областях — от математики до искусства:
- С их помощью описывают различные явления классической механики, гидродинамики, электродинамики и геофизики.
- В телекоммуникациях они позволяют моделировать электромагнитные поля в сотовой и спутниковой связи.
- В биологии — точно описывать структуру природных объектов, моделировать и предсказывать их поведение.
- Медицина использует фракталы для исследования внутренних процессов в организме человека, изучения сердечного ритма, работы кровеносных сосудов и нервной системы.
- В экономике на основе фракталов проводят анализ рынков и выявляют закономерности в поведении цен.
- В трёхмерной графике их используют для создания сложных текстур и моделей, таких как деревья, облака и морские волны.
- В искусстве и дизайне — когда нужно создать нестандартную «психоделическую» композицию, погрузить зрителя в новые измерения.
Это лишь одни из многих способов применения фракталов. Область математики, которая занимается их изучением, довольно молодая, поэтому мы продолжаем наблюдать новые открытия по сей день.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!






