Динамическое программирование — это просто. Решаем задачу о рюкзаке
Объясняем на пальцах, как использовать приёмы динамического программирования в жизни и на работе.


Вам никогда не хотелось бросить всё и уйти из дома с одним рюкзаком? Мне да, но институт, экзамены, сессия родственники, ипотека, кот — так что не вариант.
Но если бы я собирала такой рюкзак, то положила бы в него вещи, которые можно продать побыстрее и подороже, — чтобы выручить денег для новой жизни в новом месте.
Обозначим задачу
У нас есть довольно вместительный рюкзак и дорогие вещи, которые можно в него положить. Но вот беда — лямки рюкзака выдерживают, скажем, четыре килограмма, не больше.
А выбираем мы:
- из ноутбука, который весит три килограмма и стоит 2 000 долларов;
- бензопилы (ею ещё можно отмахиваться от назойливых попутчиков) — четыре килограмма мощи, которые обойдутся новому владельцу в 3 000 долларов;
- и мини-гитары — весит килограмм, а продать её можно за 1 500 долларов.
Нам нужно выбрать вещи наибольшей общей стоимости и не забывать про хилые лямки рюкзака.
Решаем вручную
Самый очевидный выход
Это полный перебор, конечно! Из трёх предметов можно составить всего восемь комбинаций. Подсчитаем стоимость для каждой и выберем самый выгодный вариант:
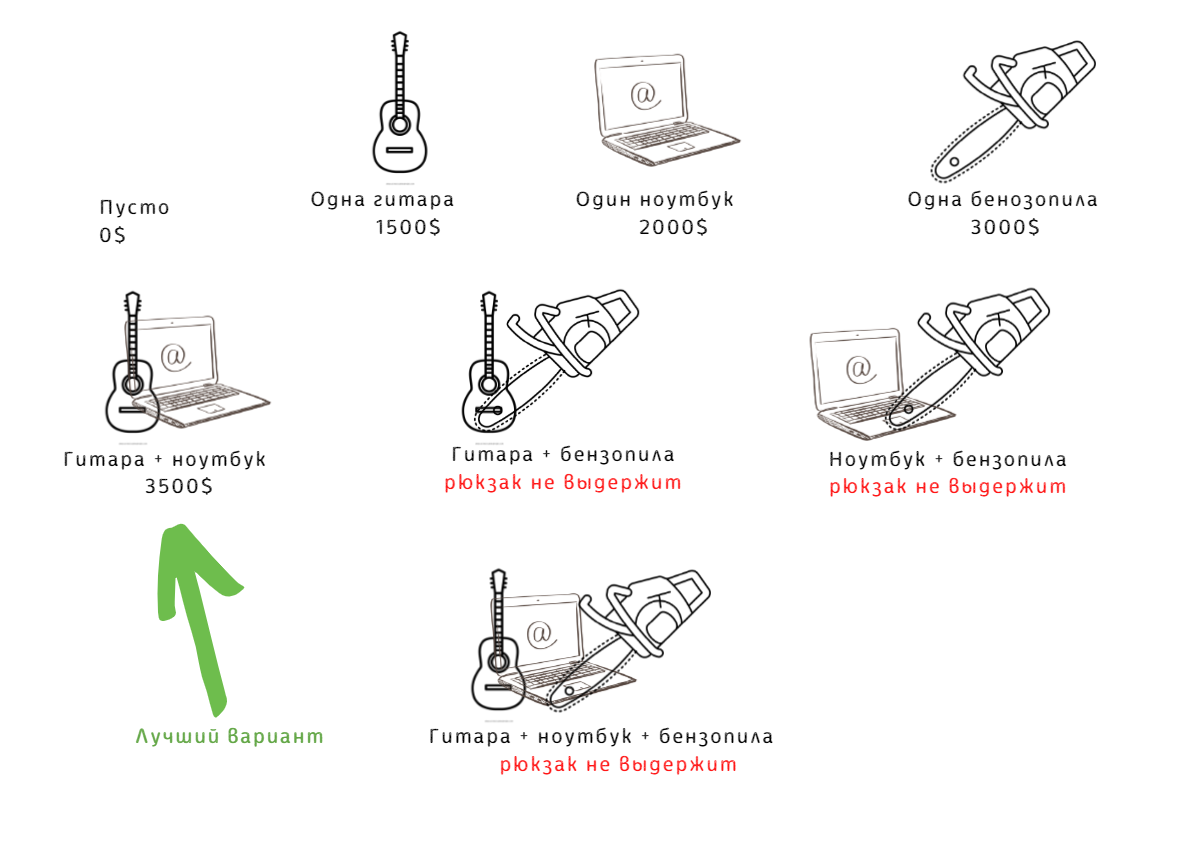
Пока предметов только три — вполне себе годное решение, но добавим ещё один — и вариантов станет 16, а для пяти их будет уже 32.
С добавлением каждого нового предмета число комбинаций удваивается, так что сложность такого алгоритма — O(2n). Это медленный способ.
Приблизительное решение
Применим так называемый жадный алгоритм: на каждом шаге добавляем в рюкзак самый дорогой предмет, пока лимит веса не превышен.
В случае с нашими предметами — одним шагом дело бы и закончилось. Мы сразу же взяли бы бензопилу за 3 000 долларов, потому что она самая дорогая. А при добавлении любого нового предмета в рюкзаке уже был бы перевес.
Было ли наше решение оптимальным? Нет, потому что гитару на пару с ноутбуком наш рюкзак тоже выдержит, но стоят они 1 500 долларов + 2 000 долларов = 3 500 долларов, что больше 3 000 долларов.
Оптимальное решение
Воспользуемся приёмами динамического программирования. Разобьём задачу на подзадачи и будем последовательно их решать. При этом на каждом следующем шаге используем результаты предыдущего.
Наглядно это можно представить в виде таблицы. Её ещё называют таблицей мемоизации. Столбцы нашей соответствуют килограммам (от одного до четырёх), а строки — предметам (гитара, бензопила, ноутбук).
| 1 кг | 2 кг | 3 кг | 4 кг | |
|---|---|---|---|---|
| гитара | ||||
| бензопила | ||||
| ноутбук |
Таблица до заполнения
На пересечении, в ячейках, будем записывать общую стоимость предметов в рюкзаке.
Гитара
Для каждого столбца (та или иная грузоподъёмность рюкзака) нужно решить: класть гитару в рюкзак или нет.
Так как гитара весит всего один килограмм, то она влезет уже на первом шаге. Поэтому в каждой ячейке первой строки напишем 1 500 — стоимость гитары.
Мы заполнили строку целиком и узнали, что промежуточный максимум для рюкзака в четыре килограмма составляет 1500 долларов.
| 1 кг | 2 кг | 3 кг | 4 кг | |
|---|---|---|---|---|
| гитара | 1 500 | 1 500 | 1 500 | 1 500 |
| бензопила | ||||
| ноутбук |
Таблица для первого предмета — гитары
Бензопила
На следующем этапе рассматриваем двух кандидатов — гитару и бензопилу.
В рюкзаки, рассчитанные на один, два или три килограмма, бензопилу не положить, так что оставляем там гитару и максимум стоимости вещей 1 500 долларов. А вот для случая «четыре килограмма» обновляем максимум: кладём бензопилу стоимостью 3 000 долларов.
| 1 кг | 2 кг | 3 кг | 4 кг | |
|---|---|---|---|---|
| гитара | 1 500 | 1 500 | 1 500 | 1 500 |
| бензопила | 1 500 | 1 500 | 1 500 | 3 000 |
| ноутбук |
Таблица для двух предметов — гитары и бензопилы
Ноутбук
Добавим последний предмет — ноутбук.
Для первых двух столбцов ничего не меняется, так как ничего, кроме гитары, в рюкзаки с грузоподъёмностью один и два килограмма положить не получится.
Зато в трёхкилограммовый рюкзак уже можно вместо гитары положить ноутбук — он дороже, обновляем максимум в этом столбце до 2 000 долларов.
Интереснее всего ситуация в последней ячейке: мы можем положить ноутбук, но он весит всего три килограмма, ещё один килограмм остаётся свободным.
И вот тут, наконец, пригодятся промежуточные результаты: мы узнали на предыдущих шагах максимальную стоимость для рюкзака, который выдерживает один килограмм, — она равна 1 500 долларов.
В итоге получаем ноутбук + гитара = 3 500 долларов, это больше предыдущего максимума в 3 000 долларов. Так что ответ в задаче — 3 500 долларов.
| 1 кг | 2 кг | 3 кг | 4 кг | |
|---|---|---|---|---|
| гитара | 1 500 | 1 500 | 1 500 | 1 500 |
| бензопила | 1 500 | 1 500 | 1 500 | 3 000 |
| ноутбук | 1 500 | 1 500 | 2 000 | 3500 |
Таблица для всех трёх предметов
В общем случае формула для стоимости в каждой ячейке выглядит так:
S[i, j] = max (S[i−1, j], цена i-го предмета + S[i−1, j−вес i-го предмета]),
где i — номер строки, j — столбца.
То есть на каждом шаге мы выбираем между предыдущим максимумом и суммой, которую составляют стоимость текущего предмета и максимальная цена незанятого веса.
Решим на Java
Определим класс для вещей, которые можно положить в рюкзак:
public static class Item {
private final String name; //название вещи
private final int weight; //вес
private final int price; //стоимость
public Item(String name, int weight, int price) {
this.name = name;
this.weight = weight;
this.price = price;
}
public String getName() {
return name;
}
public int getWeight() {
return weight;
}
public int getPrice() {
return price;
}
}И класс для промежуточного состояния — содержимого ячейки таблицы. Будем хранить, какие вещи на этом этапе лежат в рюкзаке, а также их общую стоимость.
public Backpack(Item[] items, int price) {
this.items = items;
this.price = price;
}
public Item[] getItems() {
return items;
}
public int getPrice() {
return price;
}
//Описание состояния рюкзака
public String getDescription() {
return items == null ? "" : Arrays.stream(items).map(Item::getName).collect(Collectors.joining("+")) + "-" + getPrice();
}
}
Чтобы сократить запись и уменьшить количество циклов, здесь и далее приводим вставки кода с использованием Java Stream API. Если вы мало знакомы с такой записью, почитайте о стримах здесь.
Определимся с исходными данными:
int n = 3; //число строк = число вещей
int k = 4; //грузоподъёмность рюкзака
//массив вещей
Item[] items = {new Item("гитара", 1, 1500),
new Item("бензопила", 4, 3000),
new Item("ноутбук", 3, 2000)};
//массив промежуточных состояний рюкзака
Backpack[][] bp = new Backpack[n + 1][k + 1];А теперь реализуем на Java описанный выше алгоритм заполнения таблицы:
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < k + 1; j++) {
if (i == 0 || j == 0) { //нулевую строку и столбец заполняем нулями
bp[i][j] = new Backpack(new Item[]{}, 0);
} else if (i == 1) {
/*первая строка заполняется просто: первый предмет кладём или не кладём в зависимости от веса*/
bp[1][j] = items[0].getWeight() <= j ? new Backpack(new Item[]{items[0]}, items[0].getPrice())
: new Backpack(new Item[]{}, 0);
} else {
if (items[i - 1].getWeight() > j) //если очередной предмет не влезает в рюкзак,
bp[i][j] = bp[i - 1][j]; //записываем предыдущий максимум
else {
/*рассчитаем цену очередного предмета + максимальную цену для (максимально возможный для рюкзака вес − вес предмета)*/
int newPrice = items[i - 1].getPrice() + bp[i - 1][j - items[i - 1].getWeight()].getPrice();
if (bp[i - 1][j].getPrice() > newPrice) //если предыдущий максимум больше
bp[i][j] = bp[i - 1][j]; //запишем его
else {
/*иначе фиксируем новый максимум: текущий предмет + стоимость свободного пространства*/
bp[i][j] = new Backpack(Stream.concat(Arrays.stream(new Item[]{items[i - 1]}),
Arrays.stream(bp[i - 1][j - items[i - 1].getWeight()].getItems())).toArray(Item[]::new), newPrice);
}
}
}
}
}Напишем небольшой фрагмент кода для вывода полученной в итоге таблицы:
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < k + 1; j++) {
System.out.print(bp[i][j].getDescription() + " ");
}
System.out.print("\n");
}И убедимся, что результат запуска этого фрагмента совпадает с таблицей, которую мы получили вручную:
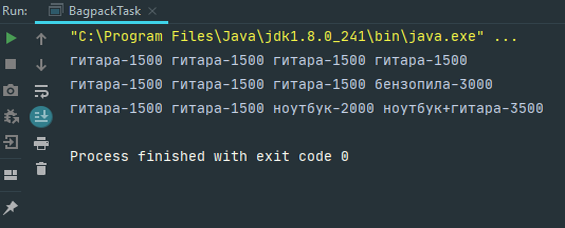
Дело за малым — найти в этой таблице ответ на задачу: какие предметы нужно взять и сколько за них в лучшем случае можно выручить. Ответ находится в последнем столбце таблицы: именно в нём записана стоимость предметов для четырёх килограммов — максимально допустимого веса нашего рюкзака.
Так что нужно перебрать все записи в этом столбце и найти сочетание с наибольшей стоимостью. Это можно сделать так:
List<Backpack> lastColumn = Arrays.stream(backpack).map(row -> row[row.length - 1]).collect(Collectors.toList());
Backpack backpackWithMax = lastColumn.stream().max(Comparator.comparing(Backpack::getPrice)).orElse(new Backpack(null, 0));
System.out.println(backpackWithMax.getDescription());
На что ещё способен наш алгоритм
Чтобы отдохнуть от рутины, необязательно уходить из дома насовсем, достаточно выбраться в новое интересное место на пару-тройку дней.
Скажем, вы приезжаете в Санкт-Петербург на выходные и хотите увидеть как можно больше достопримечательностей. Каждую вы оценили в баллах — насколько сильно вам это место интересно. Кроме того, прикинули время, которое уйдёт на осмотр.
Посмотрим, что там у вас:
- Эрмитаж — восемь баллов и половина дня;
- фонтаны в Петергофе — десять баллов и день;
- сфинксы на набережной — семь баллов и четверть дня;
- Исаакиевский собор с колокольней — шесть баллов и полдня;
- и так далее на ваш вкус.
По сути это ровно та же задача о рюкзаке. Только грузоподъёмность — это дни (у вас их два), стоимость — оценка в баллах, вес — время, которое уходит на осмотр. Нужно найти комбинацию достопримечательностей с наивысшей оценкой.
Для решения подойдёт таблица с шагом в четверть дня. В ней будет восемь столбцов, а строк столько, сколько достопримечательностей вы хотите увидеть.
Так вы без труда составите оптимальный план.
Что дальше?
Приходите на курс «Алгоритмы и структуры данных для разработчиков». Это та необходимая база, которая структурирует мышление — и меняет подход, делает программиста из обычного кодера. Студенты решают самые разные задачи, на практике осваивают важнейшие структуры данных и золотой арсенал алгоритмов, оценивают ресурсную эффективность решений и учатся оптимизировать чужой код.









