Деревья принятия решений: когда стоит их использовать и как их правильно строить
Краткий курс для начинающих и опытных разработчиков.


Бывают ситуации, в которых сложно принять решение, потому что нужно проанализировать много данных, а зависимость между входными данными и потенциальным результатом нелинейна. Например, когда компания хочет понять, стоит ли открывать новый магазин, или решает, кому поручить разработку приложения — штатной IT-команде или подрядчикам. Здесь и пригодятся деревья принятия решений.
Из этой статьи вы узнаете:
- что такое деревья принятия решений;
- когда их используют;
- какая у них структура;
- какие есть способы их построения;
- какие этапы включает создание дерева;
- как их остановить;
- когда следует подстригать ветви;
- какие преимущества и недостатки есть у алгоритма;
- где будут полезны деревья принятия решений.
Что такое дерево принятия решений
Дерево принятия решений — это метод машинного обучения, который используют, чтобы разделить большой объём входных данных на относительно небольшие группы и прогнозировать наступление события в зависимости от определённых условий.
Можно сказать, что это способ присвоения определённого «ярлыка» объекту путём поэтапной проверки заранее прописанного набора правил или простейших условий. Если представить этот процесс графически, получится древовидная схема, в которой конечные узлы соответствуют классу или решению, а промежуточные — проверяемым условиям.
Например, вот так может выглядеть дерево решений при наборе сотрудников на работу:
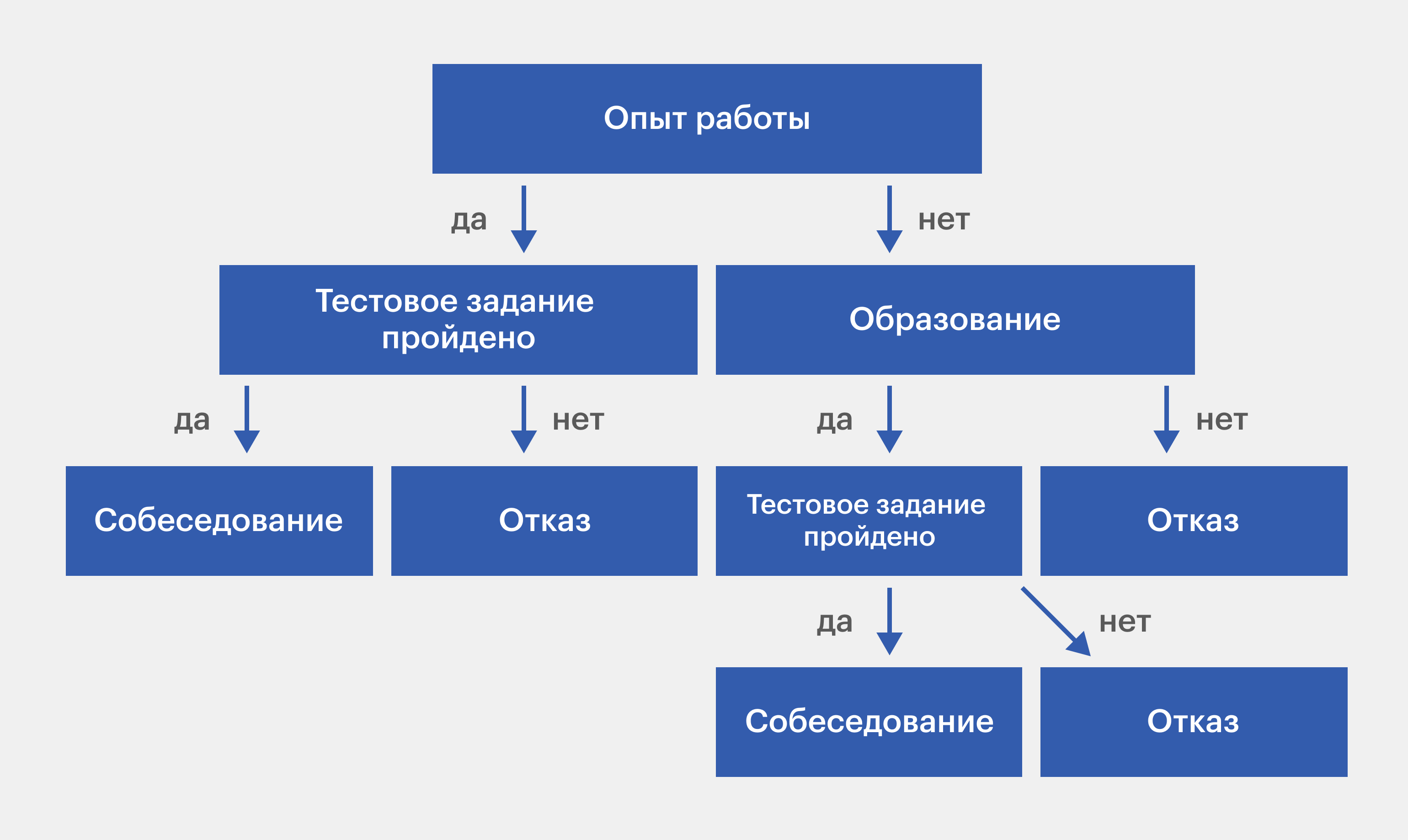
Изображение: Skillbox Media
В решении каких задач помогает дерево решений
Обычно деревья применяют, когда нужно решить следующие задачи:
- Представить данные в виде иерархической схемы или набора правил. Например, показать, как может вырасти прибыль магазина после расширения его ассортимента.
- Классифицировать объекты. Деревья помогают определить настроение пользователей по их комментариям, разделив все тексты на группы в зависимости от интонаций и эмоций.
- Сделать прогноз. Например, выяснить, как изменение графика движения транспортных судов повлияет на стоимость товара.
Структура дерева решений
Дерево принятия решений схематично можно представить в виде графа, в котором из каждой вершины, или узла принятия решений, выходят ветки. Узел без веток называется листом.
Посмотрим на пример:
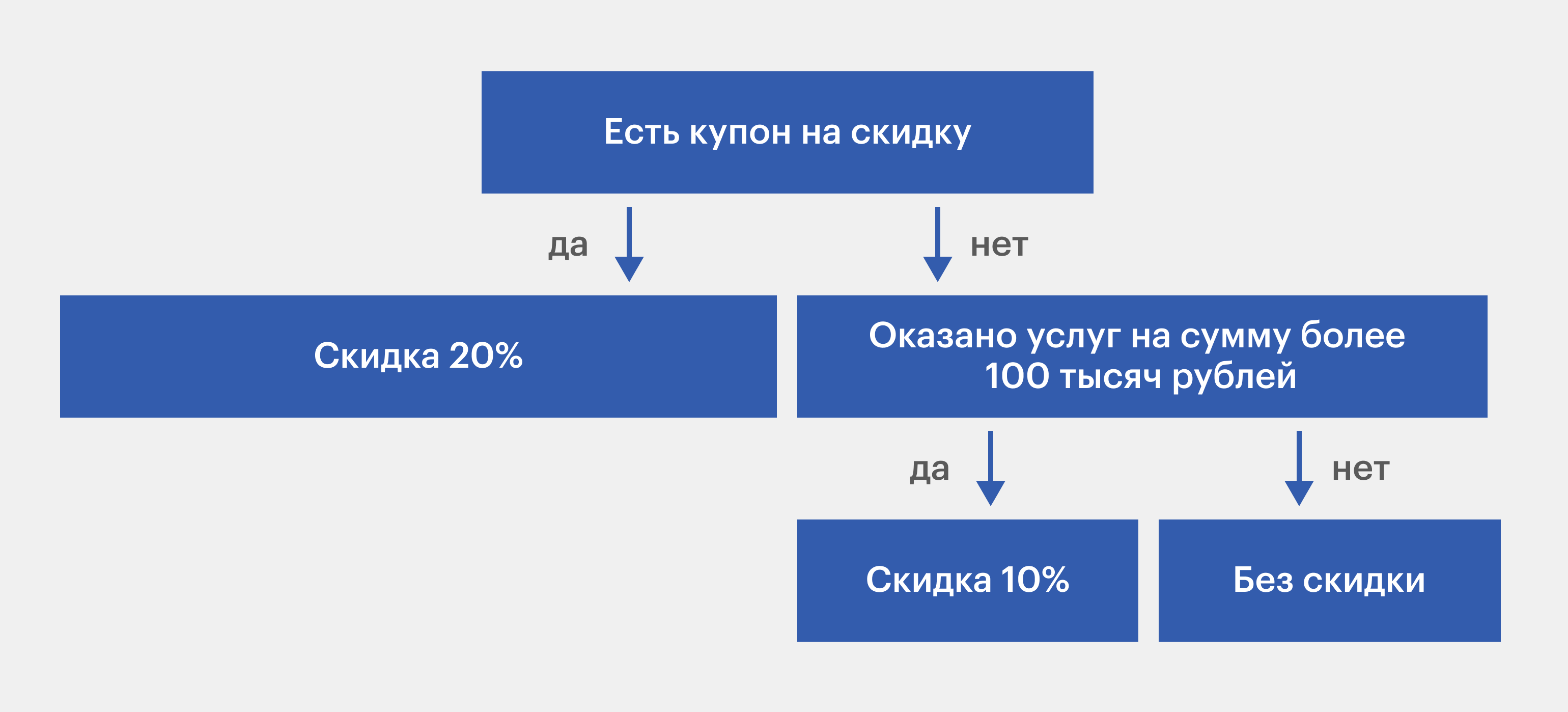
Изображение: Skillbox Media
Самый первый узел называют корневым, или решающим. В нашем случае это вопрос: «Есть купон на скидку?» Остальные узлы содержат условие, или правило в формате «если… то…», а количество выходящих из узла веток соответствует количеству вариантов ответа.
Обычно вариантов всего два — «да» или «нет»: если условие выполняется, то мы движемся по одной ветке, если нет — то по другой. То есть можно сказать, что в каждой вершине объекты, или, как их ещё называют, примеры, разбиваются на подмножества — удовлетворяющие и не удовлетворяющие условию.
Если нужно выбрать оптимальный вариант для инвестирования или объём закупок для максимизации прибыли, для каждой ветки указывают вероятность наступления нужного события.
Когда выполняется условие, при котором процесс построения дерева заканчивается, — допустим, в узле остался всего один пример, поэтому дальше выбирать не из чего, — ветка превращается в лист. Обычно листу присваивается значение целевой переменной, которая и определяет решение. Например, выдать человеку кредит в банке или нет.
Главное, что до каждого листа можно добраться только одним способом, то есть нельзя один и тот же пример разместить на нескольких листьях в разных ветках.
Как построить дерево принятия решений
На практике алгоритмы построения деревьев отличаются по нескольким признакам:
- Допустимое количество потомков в узле. То есть количество возможных вариантов ответа для узла.
- Возможность пропускать данные и значения атрибутов. Другими словами, можем ли мы их не анализировать и переходить к следующему узлу.
- Тип целевой переменной, с которой идёт работа. Переменная может быть дискретной или непрерывной. Например, переменная, в которой хранится ответ на вопрос, дать кредит или нет, принимает дискретное значение: «да» или «нет». А переменная, которая показывает цену на квартиру, может принимать любое значение из диапазона, скажем, от 2 до 10 миллионов. Это непрерывная переменная.
Деревья принятия решений можно строить прямым способом, то есть сверху вниз, и обратным — снизу вверх.
Прямой способ
Прямой способ построения деревьев принятия решений относится к «жадным» алгоритмам.
Например, при решении задачи о выдаче кредита логично отсечь кандидатов по возрасту, оставив только взрослых людей уже на первом шаге алгоритма. А при постановке диагноза лучше всего начать анализ с наиболее важного симптома.
Но этот алгоритм может не приводить к оптимальному решению. Например, при решении задачи о размене монет. Если нужно собрать 6 центов из 1-, 3- или 4-центовых монет, алгоритм на первом шаге выберет наибольший вариант — 4 — и в итоге предложит комбинацию 1 + 1 + 4, а оптимальным на самом деле будет вариант 3 + 3.
При построении деревьев прямым способом важно, чтобы в обучающей выборке были представлены все классы данных. От этого будет зависеть точность метода. Например, если мы решаем задачу про монеты, то в обучающей выборке должны быть все три варианта: 1-, 3- и 4-центовые. Во время построения деревьев они будут разбиты на неповторяющиеся подмножества, то есть отдельные варианты монет.
Показывать разбиение на классы удобно графически. Например, вот так будет разбито обучающее множество при классификации ирисов по видам, если рассматривать только два признака — ширину лепестков и чашелистиков. Каждая точка на плоскости соответствует одному набору признаков и одному виду ирисов. В общем случае, если рассматривать n признаков, то и пространство будет n-мерным.
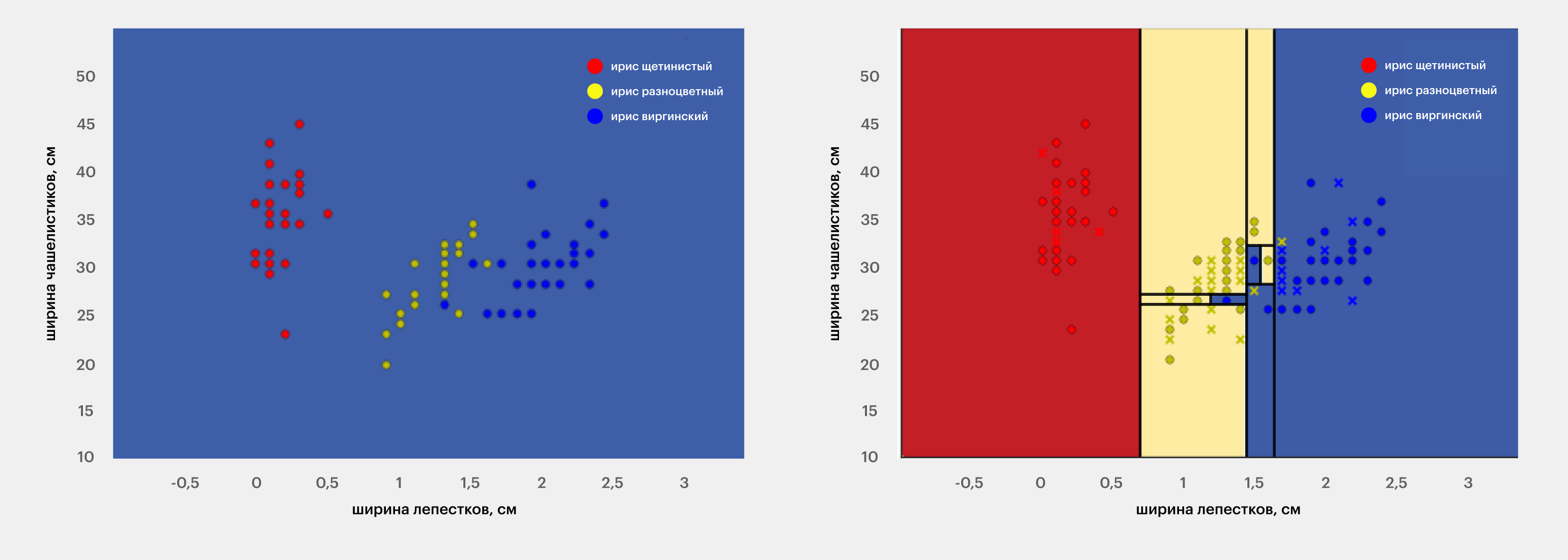
Источник: Towards Data Science
Примечание
Примеры «жадных» алгоритмов с прямым способом построения: ID3, С4.5, CART.
Обратный способ
Обратный способ построения деревьев рассмотрим на примере. Допустим, существует три инвестиционных проекта, они различаются размером первоначальных вложений и возможной прибыли, а также имеют разную вероятность потери денежных средств, то есть риски:
- Инвестиции — 250 миллионов, ожидаемая прибыль — 150 миллионов, вероятность потери — 10%.
- Инвестиции — 350 миллионов, ожидаемая прибыль — 250 миллионов, вероятность потери — 5%.
- Инвестиции — 550 миллионов, ожидаемая прибыль — 350 миллионов, вероятность потери — 20%.
Чтобы выбрать, куда стоит вложить деньги, нарисуем дерево решений и рассчитаем значение прибыли как сумму произведений, в которых первый множитель — значение, которое может принимать случайная величина, а второй — вероятность, с которой она может принимать это значение.
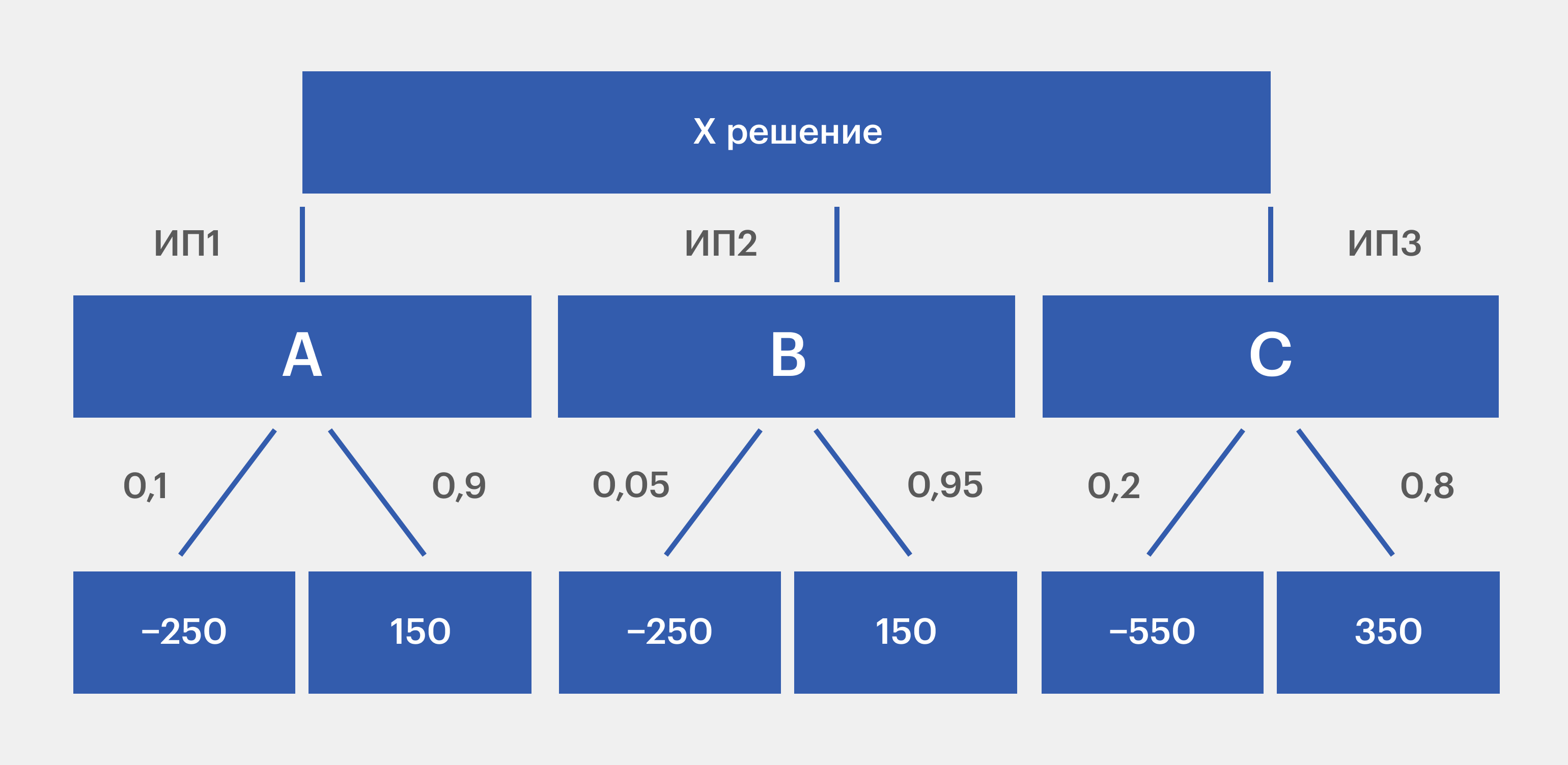
Изображение: Skillbox Media
Тогда:
- А = −250 × 0,1 + 150 × 0,9 = 110;
- В = −350 × 0,05 + 250 × 0,95 = 207,5;
- С = −550 × 0,2 + 350 × 0,8 = 170.
Оптимальный вариант — B, так как итог равен 207,5. То есть для инвестиций стоит выбрать второй проект.
Основные этапы построения дерева решений
Процесс построения дерева принятия решений включает три этапа: обучение, тестирование на наборе данных, отличном от того, на котором проводилось обучение, и верификация результатов. На последнем этапе оценивается точность метода с помощью определения верно и ошибочно классифицированных примеров.
Читайте также:
Для точности метода важны следующие этапы:
1. Выбор признака, по которому примеры будут разделяться на подмножества в конкретном узле. Разделение должно быть таким, чтобы в каждое подмножество попадали примеры, максимально близкие друг к другу по какому-либо одному значимому признаку. Благодаря этому мы сможем относить объекты к тому или иному классу.
Например, в дереве, которое разделяет целевую аудиторию на группы и считает размер скидки, зависящий от суммы оказанных услуг, не нужно анализировать возраст человека или его пол. Потому что люди любого пола и возраста могут оказаться во всех классах. То есть на размер скидки эти признаки не влияют.
Чтобы понять, что выбранный признак даёт лучший результат, чем другие признаки, можно рассчитывать энтропию (меру неопределённости) узла в дереве принятия решений, как это реализовано в алгоритмах C4.5 и ID3. Признак должен приносить наибольшее количество информации и уменьшать энтропию. Энтропия в узле может принимать значения от 0, когда все примеры относятся к одному классу, до 1, когда примеры распределяются между классами поровну.
А ещё можно использовать коэффициент Джини, как в алгоритме CART. Коэффициент Джини равен разности единицы и суммы квадратов вероятности каждого класса. Индекс равен нулю, если в узле все примеры относятся к одному классу. В таком случае говорят, что узел полностью чист. И он принимает максимальное значение (1 − 1/n), если примеры распределяются между n классами поровну. Например, при разделении населения на группы по уровню дохода коэффициент покажет, равномерно распределены доходы в обществе (коэффициент стремится к единице) или нет (коэффициент равен нулю).
Например, в задаче классификации ирисов по видам в первом узле множество будет разбито так:
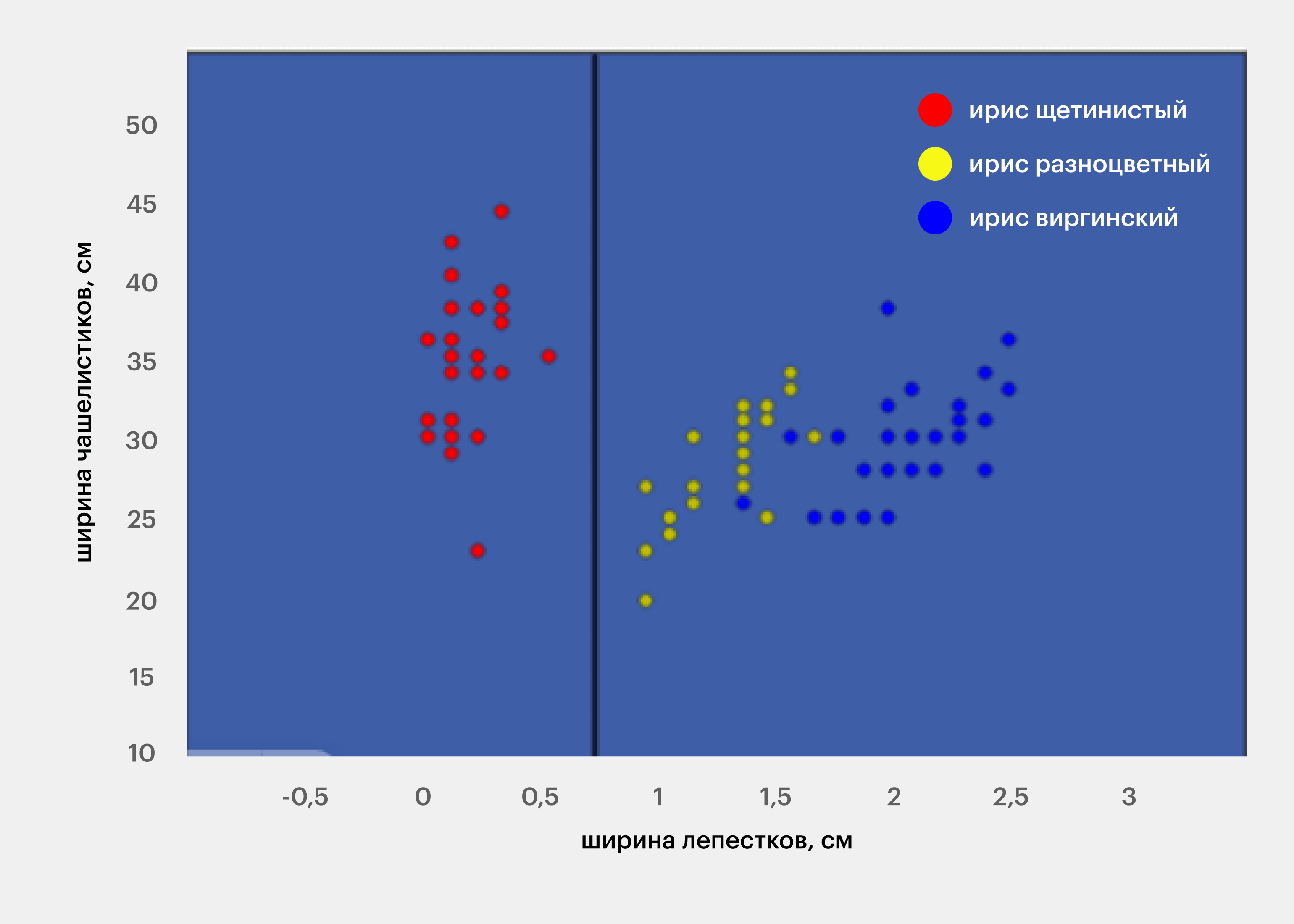
Изображение: Skillbox Media
В этом случае для левого подмножества (на рисунке — красные точки) коэффициент Джини будет равен нулю, а для правого — примерно 0,5.
2. Определение критерия остановки, то есть условия окончания обучения. Например, критерием может быть доля примеров в узле, которые можно отнести к одному классу. Если среди миллиона клиентов, у которых есть купон, только 10 человек заплатили за услуги больше 100 тысяч рублей, нет смысла разрабатывать под них отдельное предложение.
3. Упрощение дерева с помощью отсечения ветвей. Анализ построенного дерева и выявление ветвей, которые влияют на результат несущественно. Например, при поиске компании для разработки сайта можно не учитывать часовой пояс, в котором находится подрядчик, в том случае, если синхронная коммуникация не требуется.
4. Оценка точности дерева принятия решений. Если точность на этапе обучения будет высокой, а на этапе тестирования — низкой, это значит, что на этапе обучения построено слишком сложное дерево: оно эффективно только для обучающей выборки, а использовать его на реальных данных сложно.
Критерий остановки алгоритма
Алгоритм может останавливаться естественным способом — когда в листе остаётся один пример и делить становится нечего. Но практической ценности такое дерево не будет иметь из-за своей переобученности.
Чтобы построить оптимальное с точки зрения точности решений и сложности построения дерево, используют различные критерии. Например:
- максимальное количество узлов в дереве, или глубина дерева;
- минимально допустимое количество примеров в узле;
- процент верно распознанных примеров;
- доля примеров в узле, которые можно отнести к одному классу;
- степень увеличения информации и уменьшения энтропии при последующем дроблении.
Например, при разделении пользователей онлайн-магазина книг на группы нет смысла делить любителей фантастики на подгруппы по видам фантастики, если больше 98% из них предпочитают читать один из видов — например, про попаданцев.
Отсечение ветвей дерева
Заранее сложно сказать, каким должно быть оптимальное дерево решений. Один из способов понять это — построить все варианты деревьев, оценить их точность и выбрать вариант глубины с оптимальным балансом между сложностью построения и точностью. То есть, попросту говоря, решить задачу перебором всех возможных решений. Но задача поиска такого баланса не может быть однозначно решена за короткое время, то есть для её решения не существует «быстрых» алгоритмов.
Поэтому используют метод отсечения ветвей, или метод стрижки дерева. Ветви у деревьев отсекаются в направлении, обратном направлению построения деревьев. Вот общий алгоритм:
Шаг 1. Построить дерево, у которого в каждом листе останется только по одному элементу.
Шаг 2. Вычислить долю правильно распознанных примеров и количество неверно распознанных примеров.
Шаг 3. Удалить узлы, отсутствие которых минимально повлияет на показатели из шага 2. Под удалением узлов понимаем их превращение в листья.
Схематично этот процесс можно изобразить так:
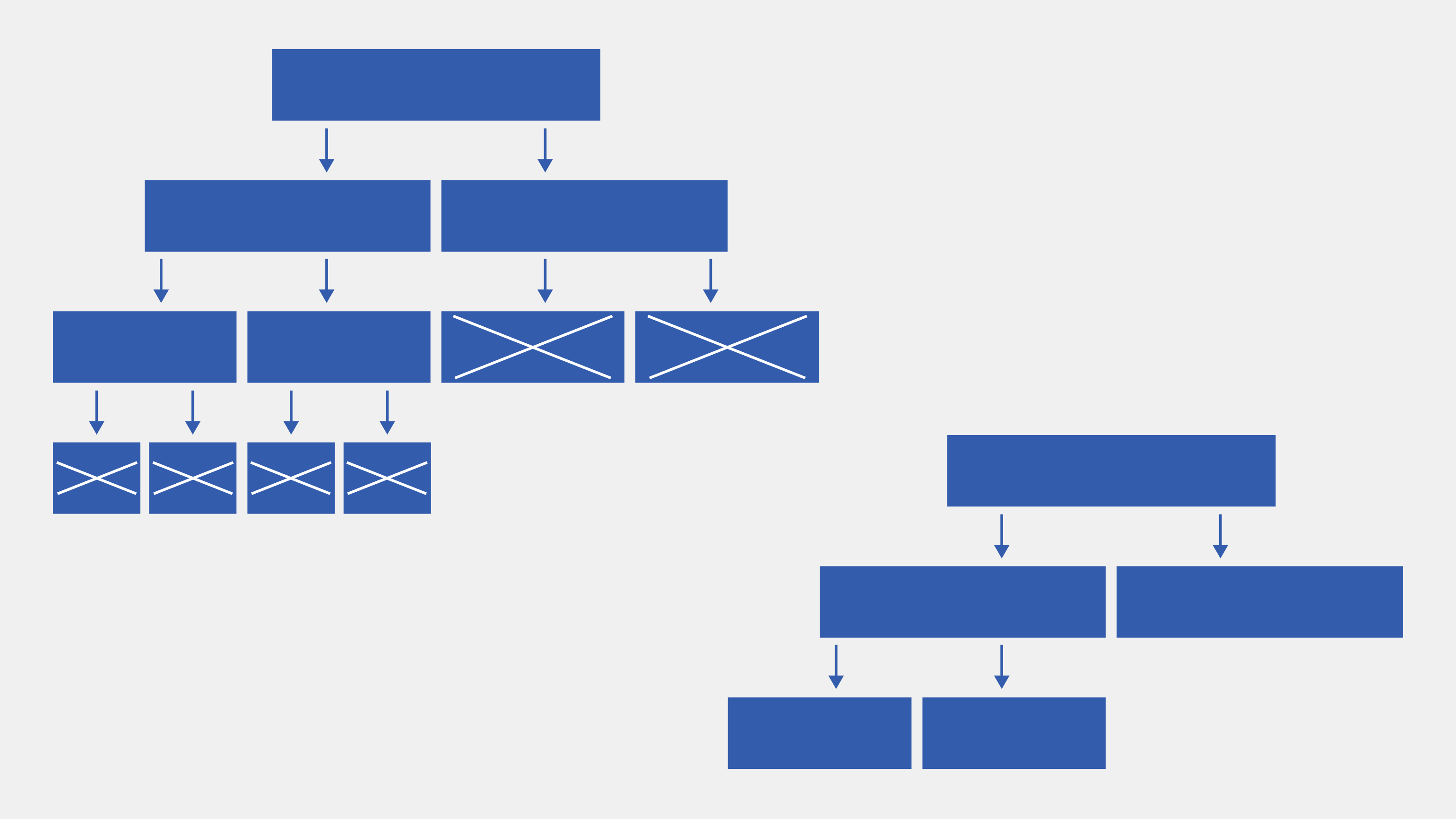
Изображение: Skillbox Media
Такой метод требует больше времени на обучение: сначала полностью строится дерево, потом рассчитываются критерии его точности. Но отсечение ветвей — более точный метод построения деревьев, чем, например, метод преждевременной остановки.
Преимущества и недостатки дерева решений
Использование дерева решений в машинном обучении имеет свои плюсы и минусы.
Преимущества:
- Просто представить информацию и решения в виде иерархической структуры и интерпретировать их.
- Подходит для работы как с дискретными, так и с непрерывными величинами.
- Позволяет работать с пропусками данных, так как дерево решений может заполнить их наиболее вероятными значениями.
Недостатки:
- Точность деревьев зависит от метода построения и содержания обучающей выборки. Одно значение, выбивающееся из ряда однородных (выброс), может повлиять на общий результат. Необходим предварительный анализ используемых в обучающей выборке данных и их подготовка.
- Точность на этапе обучения может быть выше, чем точность при эксплуатации на другом наборе данных из-за переобученности. Но это общая проблема методов машинного обучения.
Где применяют деревья решений
Ответ очевиден — там, где нужно принимать решения, но проанализировать вручную входные данные сложно из-за их огромного количества. Вот сферы, где метод распространён.
Банковский сектор и инвестиции. Например, система может принять решение о выдаче кредита после оценки возраста, уровня дохода, кредитной истории клиента, а также наличия у него недвижимости. Другие аналитические системы оценивают инвестиционные проекты и выбирают самый привлекательный, исходя из размера требуемых инвестиций и допустимых рисков.
Медицина. Проведение первичной диагностики для выявления симптомов или определения рисков развития заболевания. Например, деревья принятия решений используют при выявлении ранних признаков деменции.
Промышленность. Оценка качества продукции, подсчёт возможной прибыли — например, в зависимости от изменения времени поставок продуктов.
Сельское хозяйство и природопользование. Классификация растений и выявление стадий их роста, а также обнаружение лесных пожаров по спутниковым снимкам.
Менеджмент и маркетинг. Анализ способов модернизации сайта — силами штатных или сторонних разработчиков. Определение клиентов, которые планируют отказаться от услуг компании, на основе их транзакционной активности, чтобы затем предлагать им акции и скидки, мотивируя остаться. Построение скриптов для чат-ботов в клиентской службе и анализ текстов для определения настроения аудитории.
Метод построения деревьев широко используется в разных областях — от анализа данных в промышленности до чат-ботов в клиентских сервисах. Это один из базовых подходов в машинном обучении, его используют аналитики данных и дата-сайентисты.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!





