Что такое векторы и как их использовать
Объяснение для новичков с примерами и практикой в Google Colab.


В этой статье мы познакомимся с векторами в математике. Вы узнаете, что это такое, какие они бывают и как с ними работать. Чтобы не ограничиваться сухой теорией, мы будем запускать код на Python в бесплатном сервисе Google Colab.
Если вы никогда раньше не писали код — просто копируйте готовые примеры в Colab и нажимайте кнопку «Запустить». А если захотите поэкспериментировать, измените числа в коде и посмотрите, что произойдёт с вектором на рисунке.
Содержание
- Что такое вектор: определение и обозначение
- Основные виды векторов
- Координаты векторов
- Сложение и вычитание
Что такое вектор: определение и обозначение
Вектор — это математический объект, у которого есть два главных свойства: длина и направление. Его удобно представлять в виде стрелки или отрезка с начальной и конечной точкой. Например, вектор с координатами (3, 4) означает смещение на 3 единицы вправо и 4 единицы вверх от точки A.
Векторы часто встречаются в науке и технике: ими описывают силы, скорости, ускорения и перемещения. Главное их отличие от обычных чисел как раз в том, что они учитывают не только величину, но и направление. Так, скорость «10 м/с» — это просто число, а «ветер дует на север со скоростью 10 м/с» — это вектор.
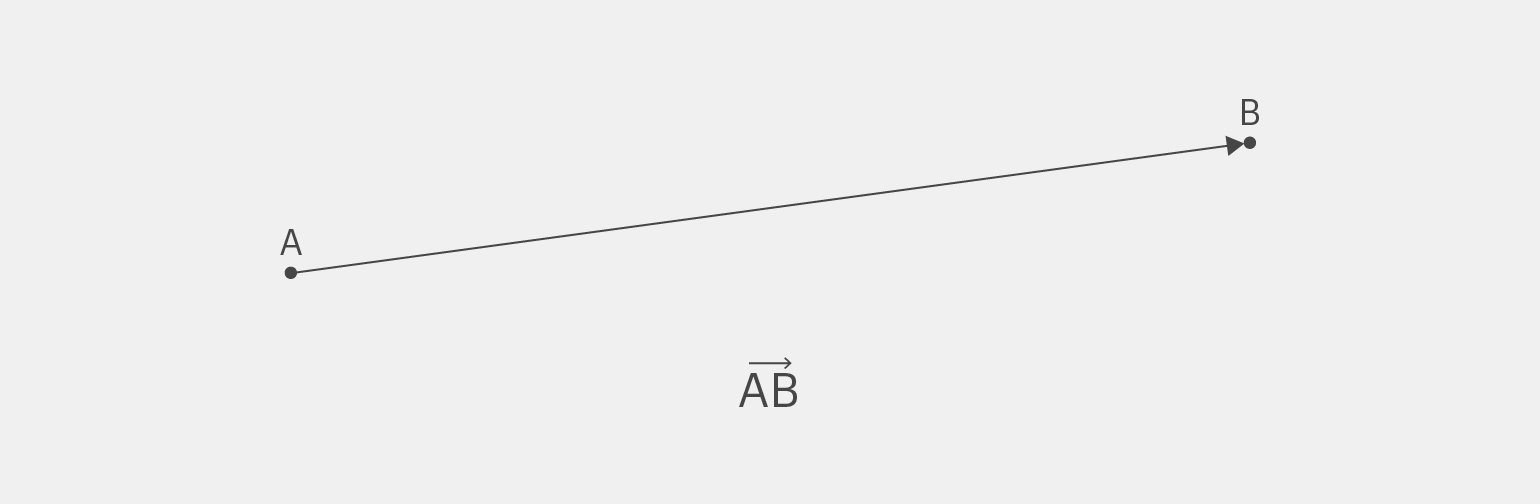
Иллюстрация: Skillbox Media
Прежде чем двигаться дальше, посмотрим, как можно записывать векторы:
- Буква со стрелкой. Самый привычный способ — латинская строчная буква с маленькой стрелкой сверху, например:
,
,
. Стрелка показывает, что это не просто число, а величина с направлением.
- Запись через начальную и конечную точки. Вектор обозначают двумя буквами: начальной и конечной. Например,
— вектор от точки A к B.
- Жирные буквы. В печатных текстах и на некоторых сайтах векторы пишут без стрелок жирными строчными буквами: a, b, v.
- Длина (модуль) вектора обозначается вертикальными линиями. Вот вариации такой записи: |
|, |
|, |
|, |
| или |a|, |v|, |b|.
- Запись через координаты. Вектор можно задать компонентами: в двумерной системе координат это
= (vx, vy), а в трёхмерной —
= (vx, vy, vz). Компоненты показывают, на сколько вектор смещается по каждой оси.
Теперь откройте Google Colab и вставьте следующий код. После запуска вы увидите красную стрелку — вектор , направленный от точки A к точке B:
import numpy as np
import matplotlib.pyplot as plt
# A — начальная точка, B — конечная точка. Меняйте их координаты, чтобы изменить вектор
A = np.array([0, 0])
B = np.array([3, 4])
AB = B - A
plt.figure()
plt.quiver(A[0], A[1], AB[0], AB[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.scatter([A[0], B[0]], [A[1], B[1]], color='black')
plt.text(A[0]-0.2, A[1]-0.2, "A")
plt.text(B[0]+0.1, B[1]+0.1, "B")
plt.xlim(-1, 5)
plt.ylim(-1, 5)
plt.axhline(0, color='gray')
plt.axvline(0, color='gray')
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.show()
Читайте также:
Виды векторов
Векторы можно классифицировать по длине, направлению, положению в пространстве и другим признакам. Давайте разберём самые основные виды.
Нулевой вектор — это вектор с нулевой длиной и без определённого направления. Его можно представить как человека, который стоит на месте и никуда не движется. В координатной системе он изображается в виде точки в начале координат и обозначается как ноль со стрелкой сверху :
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(0, 0, color='black', label='Нулевой вектор')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-0.5, 0.5); plt.ylim(-0.5, 0.5)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()Равные векторы имеют одинаковую длину и направление, даже если начинаются в разных точках. Например, вектор от A(1, 2) к B(4, 6) равен вектору от C(3, 1) к D(6, 5), поскольку оба задают одно смещение — (3, 4). Их можно сравнить с двумя велосипедистами, которые едут с одинаковой скоростью в одном направлении, но стартуют из разных мест по параллельным дорогам:
import matplotlib.pyplot as plt
plt.figure()
plt.quiver(0, 0, 2, 1, angles='xy', scale_units='xy', scale=1, color='r', label='Вектор 1')
plt.quiver(1, 1, 2, 1, angles='xy', scale_units='xy', scale=1, color='b', label='Вектор 2')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-1, 4); plt.ylim(-1, 3)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()Противоположные векторы обладают одинаковой длиной, но направлены в разные стороны. Если их сложить, то результатом всегда будет нулевой вектор. Они как два велосипедиста, которые начинают движение из одной точки и разъезжаются в противоположные стороны с одинаковой скоростью.
import matplotlib.pyplot as plt
plt.figure()
plt.quiver(0, 0, 2, 0, angles='xy', scale_units='xy', scale=1, color='r', label='Вектор 1')
plt.quiver(0, 0, -2, 0, angles='xy', scale_units='xy', scale=1, color='b', label='Вектор 2')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-3, 3); plt.ylim(-1, 1)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()Ортогональные векторы образуют угол 90°, а их скалярное произведение равно нулю. Представьте наших велосипедистов на перекрёстке: если одного отправить на север, а другого — на восток, то их траектории будут ортогональны:
import matplotlib.pyplot as plt
plt.figure()
plt.quiver(0, 0, 2, 0, angles='xy', scale_units='xy', scale=1, color='r', label='Вектор 1')
plt.quiver(0, 0, 0, 2, angles='xy', scale_units='xy', scale=1, color='b', label='Вектор 2')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-1, 3); plt.ylim(-1, 3)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()Свободный вектор можно перемещать параллельно самому себе в любую точку пространства без изменения его длины и направления. Такие векторы считаются равными, даже если они начинаются в разных точках. Представьте автомобиль: неважно, по какой улице он едет, — если его скорость и направление остаются прежними, то с точки зрения математики это всё тот же вектор:
import matplotlib.pyplot as plt
plt.figure()
plt.quiver(0, 0, 2, 1, angles='xy', scale_units='xy', scale=1, color='orange', label='Вектор 1')
plt.quiver(2, 2, 2, 1, angles='xy', scale_units='xy', scale=1, color='green', alpha=0.6, label='Вектор 2 (перемещённый)')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-1, 5); plt.ylim(-1, 4)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()Позиционный вектор соединяет начало координат с выбранной точкой и определяет её положение в пространстве. Это как путь от вашего дома до магазина: маршрут всегда начинается в нуле и ведёт к конкретной точке:
import matplotlib.pyplot as plt
plt.figure()
plt.quiver(0, 0, 2, 3, angles='xy', scale_units='xy', scale=1, color='brown', label='Позиционный вектор')
plt.scatter(2, 3, color='black')
plt.axhline(0, color='gray'); plt.axvline(0, color='gray')
plt.xlim(-1, 4); plt.ylim(-1, 4)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
ax.locator_params(nbins=5)
plt.legend()
plt.grid(True)
plt.show()
Читайте также:
Как определить координаты вектора
Помимо длины и направления, вектор можно описать с помощью координат — чисел, которые показывают, насколько он смещается по каждой из осей координатной плоскости. Если вектор начинается в начале координат A(0,0), то его координаты совпадают с координатами конечной точки. Например, если конец вектора находится в точке B(3,4), то и координаты вектора будут (3,4).
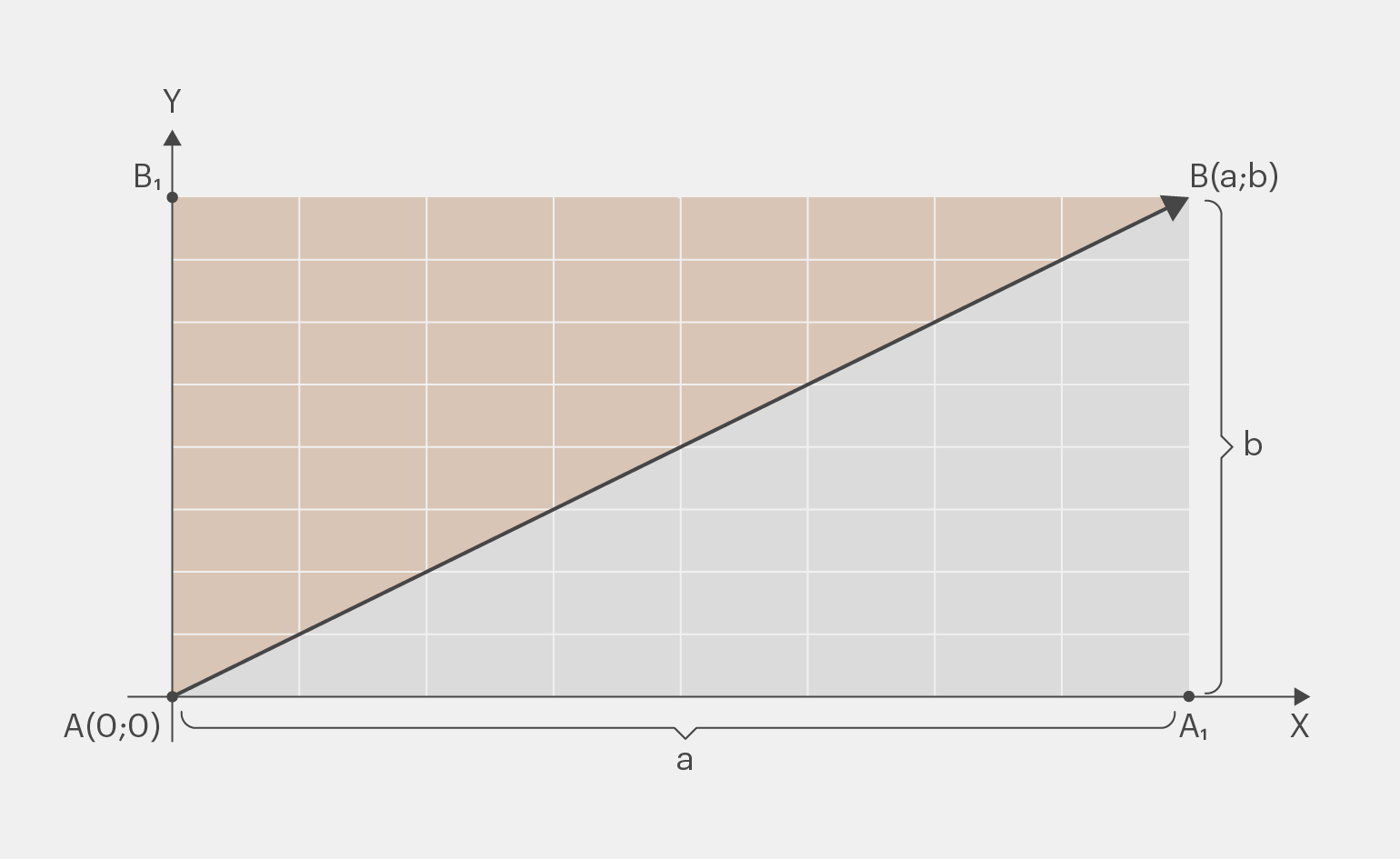
Иллюстрация: Skillbox Media
Для остальных случаев координаты вектора вычисляют как разность координат его конечной и начальной точек: = (x₂ − x₁, y₂ − y₁). Рассмотрим два примера:
- вектор
, у которого начальная точка A(1, 2), а конечная — B(5, 5);
- вектор
с начальной точкой C(−5, −6), и конечной — D(−1, −3).
Вектор имеет координаты (5 − 1, 5 − 2) = (4, 3), а вектор
— (−1 − (−5), −3 − (−6)) = (4, 3). Поскольку у обоих векторов одинаковые координаты (4, 3), они равны: их длина и направление совпадают, хотя они и начинаются в разных точках. Запустите код, чтобы увидеть векторы
и
на координатной плоскости:
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
# Меняйте координаты, чтобы построить другие векторы
A = np.array([1, 2])
B = np.array([5, 5])
C = np.array([-5, -6])
D = np.array([-1, -3])
AB = B - A
CD = D - C
AB_tuple = tuple(map(int, AB))
CD_tuple = tuple(map(int, CD))
plt.quiver(A[0], A[1], AB[0], AB[1], angles='xy', scale_units='xy', scale=1,
color='r', label=f'AB = {AB_tuple}')
plt.quiver(C[0], C[1], CD[0], CD[1], angles='xy', scale_units='xy', scale=1,
color='b', label=f'CD = {CD_tuple}')
for p, name in zip([A, B, C, D], ['A', 'B', 'C', 'D']):
plt.scatter(p[0], p[1], color='black')
plt.text(p[0] + 0.1, p[1] + 0.1, name)
plt.axhline(0, color='gray')
plt.axvline(0, color='gray')
plt.xlim(-7, 7)
plt.ylim(-7, 7)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
ax.tick_params(axis='both', labelsize=8)
plt.grid(True)
plt.legend()
plt.show()
Читайте также:
Сложение и вычитание векторов
Сложение и вычитание векторов позволяют находить результирующие перемещения, силы или скорости. Это важно в задачах физики, математики и инженерии, где часто приходится учитывать сразу несколько воздействий.
Для понимания представьте человека, который делает три шага на восток, а затем четыре шага на север. Его итоговое смещение можно найти как сумму двух векторов. А если нужно определить, с какой скоростью один автомобиль приближается к другому, то для этого вычисляют разность векторов скорости.
Есть несколько способов сложения и вычитания векторов. Но поскольку мы только знакомимся с темой, рассмотрим самый простой — алгебраический метод. Его суть в том, что координаты векторов складываются или вычитаются по компонентам. Например, у нас есть два вектора = (ax, ay) и
= (bx, by). Тогда их суммарный вектор будет с такими координатами:
+
= (ax+bx , ay+by).
Для примера возьмём векторы = (2, 1) и
= (1, 3). Тогда их сумма равна:
+
= (2 + 1, 1 + 3) = (3, 4). Посмотрите, как это выглядит на графике:
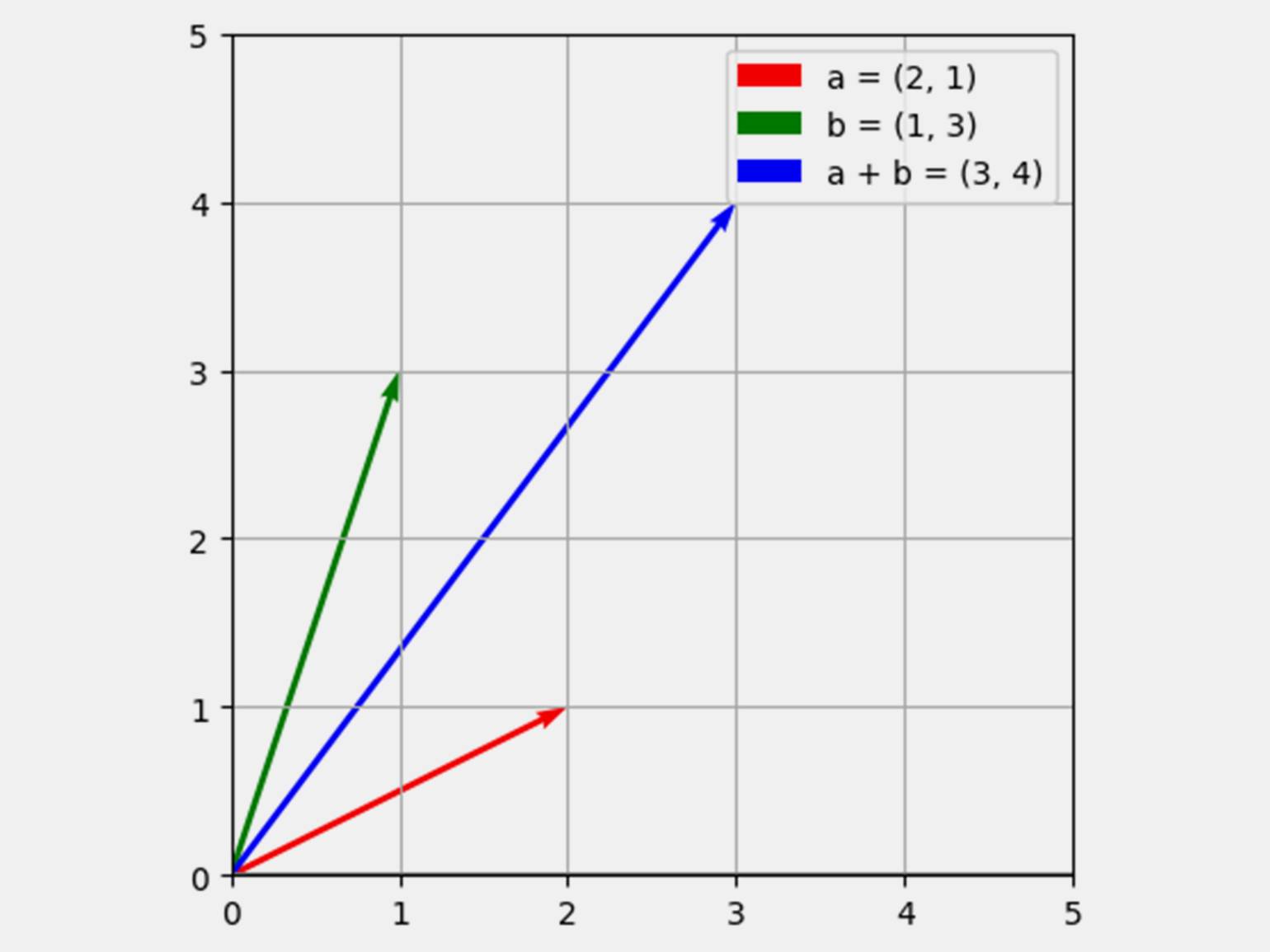
А вот код, который поможет построить такой график для сложения векторов:
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
# Меняйте координаты векторов для экспериментов
a = np.array([2, 1])
b = np.array([1, 3])
c = a + b
a_tuple = tuple(map(int, a))
b_tuple = tuple(map(int, b))
c_tuple = tuple(map(int, c))
plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1,
color='r', label=f'a = {a_tuple}')
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1,
color='g', label=f'b = {b_tuple}')
plt.quiver(0, 0, c[0], c[1], angles='xy', scale_units='xy', scale=1,
color='b', label=f'a + b = {c_tuple}')
plt.axhline(0, color='gray')
plt.axvline(0, color='gray')
plt.xlim(0, 5)
plt.ylim(0, 5)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
plt.legend()
plt.grid(True)
plt.show()Продолжим с векторами = (2, 1) и
= (1, 3), только теперь найдём их разность. Считаем:
—
= (2 — 1, 1 — 3) = (1, −2). И для наглядности создадим новый график:
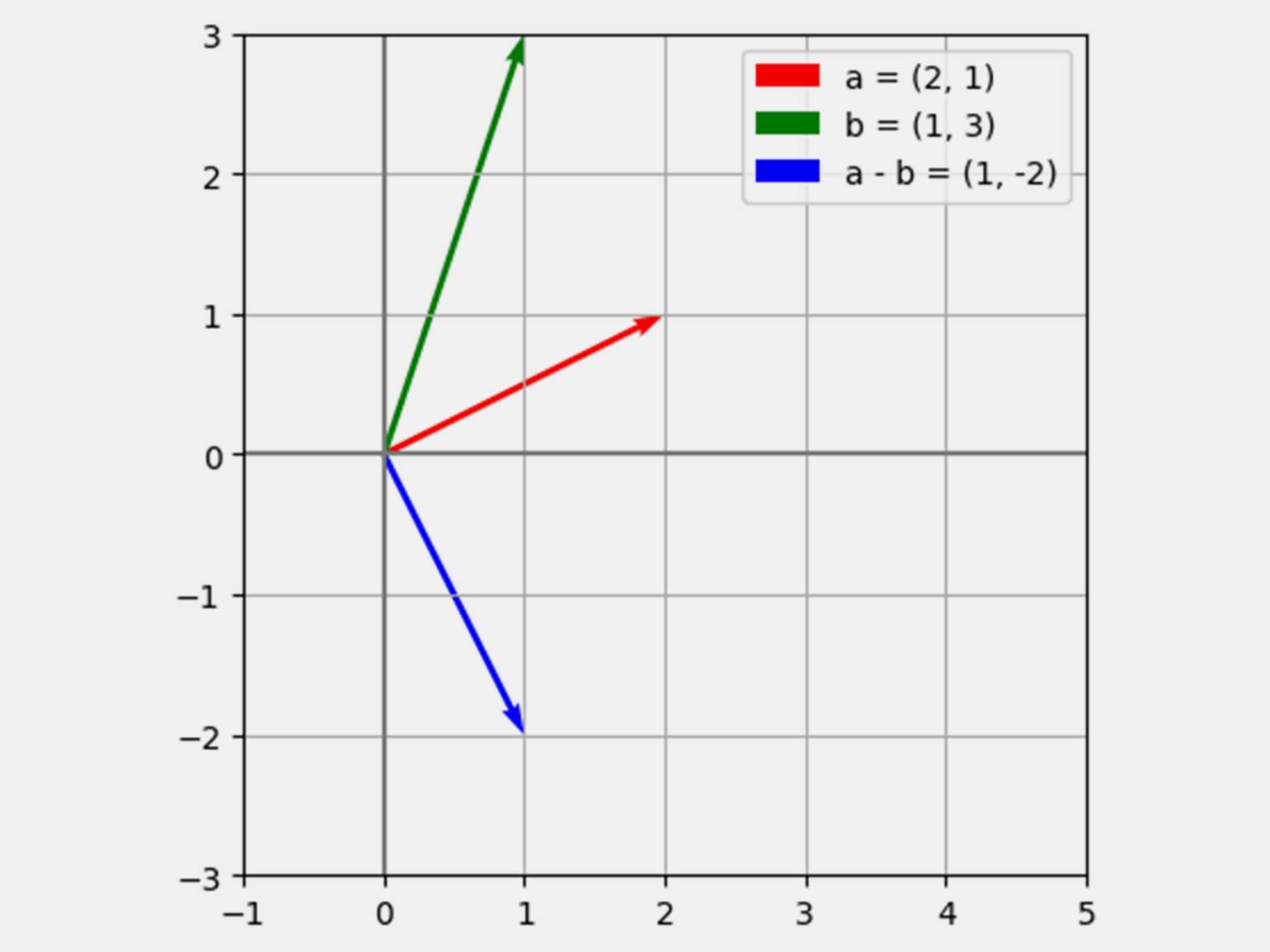
Оформляем код для Google Colab — обязательно поэкспериментируйте:
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
# Меняйте координаты и получайте разный результат вычитания векторов
a = np.array([2, 1])
b = np.array([1, 3])
d = a - b
a_tuple = tuple(map(int, a))
b_tuple = tuple(map(int, b))
d_tuple = tuple(map(int, d))
plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1,
color='r', label=f'a = {a_tuple}')
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1,
color='g', label=f'b = {b_tuple}')
plt.quiver(0, 0, d[0], d[1], angles='xy', scale_units='xy', scale=1,
color='b', label=f'a - b = {d_tuple}')
plt.axhline(0, color='gray')
plt.axvline(0, color='gray')
plt.xlim(-1, 5)
plt.ylim(-3, 3)
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
plt.legend()
plt.grid(True)
plt.show()Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!
Python для всех
Вы освоите Python на практике и создадите проекты для портфолио — телеграм-бот, веб-парсер и сайт с нуля. А ещё получите готовый план выхода на удалёнку и фриланс. Спикер — руководитель отдела разработки в «Сбере».
Пройти бесплатно



