Что такое теория игр и как она помогает побеждать
Изучаешь один раз — пользуешься всю жизнь.


Многие считают, что теория игр — это что-то про шахматы, «Монополию» и другие игры, за которыми мы так любим проводить время в компании друзей. На деле же её возможности куда шире — она помогает строить оптимальные стратегии почти во всех сферах человеческой жизни: от воспитания детей и переговоров о зарплате до политики и data science.
В этой статье мы разберёмся, что это за теория такая, как она помогает в реальной жизни и почему быть эгоистом зачастую выгоднее, чем идти на компромиссы.

Статью проверил
Пётр Емельянов
Эксперт Skillbox, CEO в Bloomtech, специалист по информационной безопасности и анализу данных. Опыт в IT — 20 лет.
Что такое теория игр
Теория игр — это раздел математики, который изучает поведение участников игры. Под игрой понимается любая ситуация, где конфликтуют интересы минимум двух людей. Это могут быть шахматы, президентские выборы, голосование в ООН, королевская битва Fortnite — что угодно.
Смысл теории игр в том, чтобы предсказать, как действия и решения одних игроков влияют на других. Давайте разберёмся, как это работает, на примере знакомой многим истории с утренним часом пик.
Ситуация: вы просыпаетесь утром и понимаете, что опаздываете на работу. Вам нужно как можно быстрее добраться до офиса — но помимо вас схожей проблемой озадачены другие 200 тысяч жителей микрорайона. Варианты у всех приблизительно одинаковые: спуститься в метро или поехать по земле — на автобусе, такси или на своей машине.
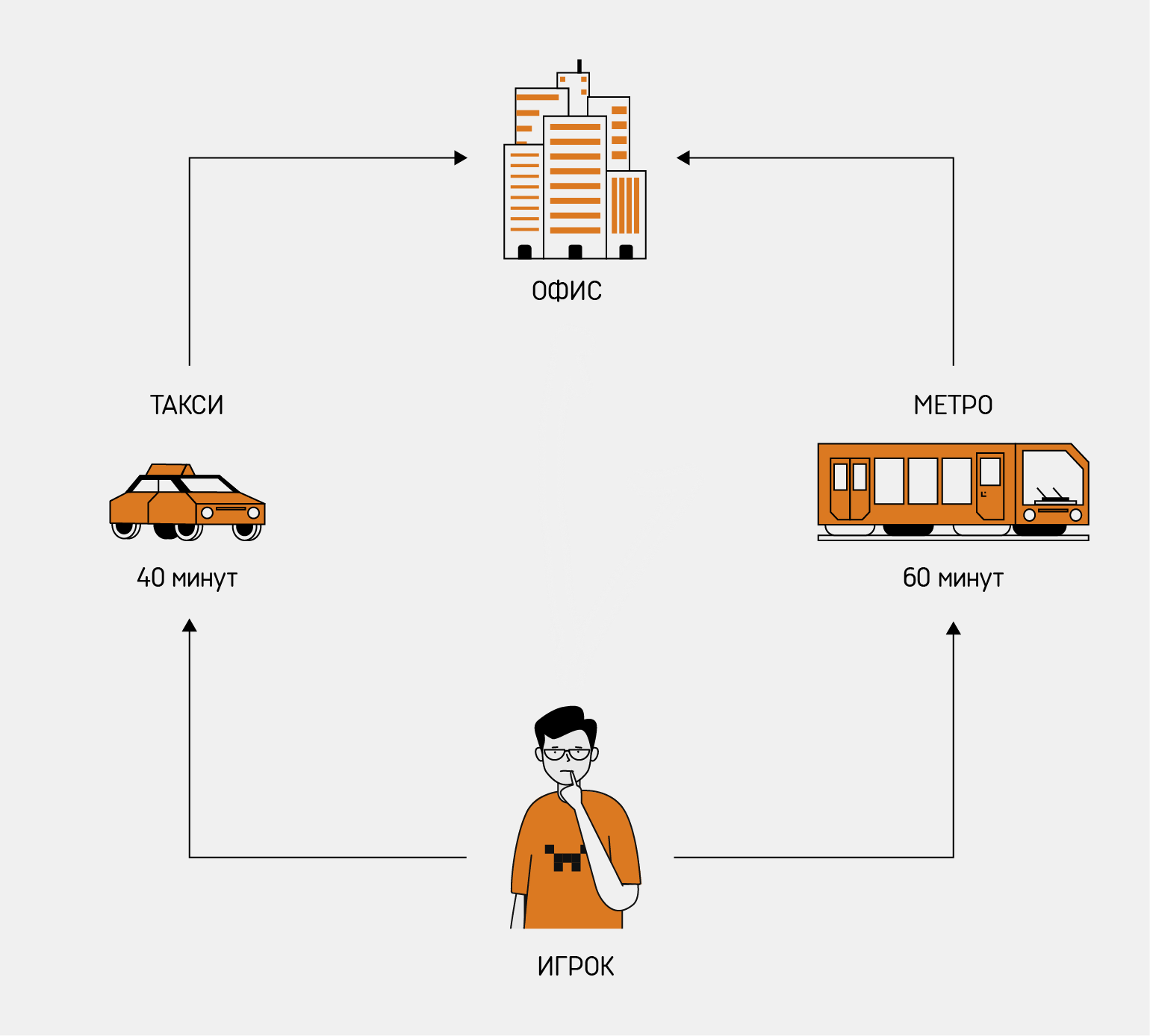
Иллюстрация: Оля Ежак для Skillbox Media
С точки зрения теории игр вы и другие жители района — это участники игры, объединённые одинаковой целью: как можно быстрее попасть из одной локации в другую. И успех каждого участника будет зависеть не только от его действий, но и от действий конкурентов.
Например, вы решили поехать на такси. Благодаря «Картам» вы уверены, что успеете, — поездка до офиса займёт 40 минут. Но если все жители решат поехать по земле, о таком времени можно будет забыть: выехав из дома, вы попадёте в пробку, виновником которой сами отчасти и станете. К тому же высокий спрос подогреет цену и вы заплатите за поездку целое состояние.
Окей, допустим, вы оказались хитрее и решили доехать на метро. Пускай вы и опоздаете на работу, зато будете точно знать на сколько: время в пути давно посчитано и составит, скажем, 35 минут — плюс 25 минут на то, чтобы доехать до метро, спуститься и подняться на эскалаторе.
Вариант с метро кажется оптимальным — но если большинство жителей района решат поступить так же, пиши пропало. Вас ждут:
- пробки на пути к метро;
- очереди на кассе и эскалаторах;
- толкучка на станции, из-за которой, возможно, придётся пропустить пару составов.
Получается, что лучший способ победить в этой игре — это попробовать угадать действия других жителей и найти такое решение, при котором будут учтены все возможные ситуации. Именно этим и занимается теория игр.
Пример оптимального решения в истории с пробками — арендовать самокат. Да, возможно, вас немного обдаст ветром и дорожной пылью, зато уже через 50 минут вы будете на месте — и никакой толкучки и пробок. К тому же сейчас лето и новую велодорожку надо оценить — в общем, берём.
Что такое игра
Технически игра — это любая ситуация, в которой конфликтуют интересы разных людей. У каждого игрока есть цель и несколько вариантов действий. От того, какое действие вы выберете, зависит результат других игроков — и наоборот. А ещё в игре должны быть правила, известные всем участникам.
Например, в королевской битве Fortnite соревнуются 100 игроков, где у каждого есть цель — остаться последним из выживших. Понятно, что эти интересы конфликтуют — не может же каждый быть тем самым последним выжившим. Поэтому приходится выкручиваться — выбирать такие действия, чтобы и других по возможности нейтрализовать, и самому не попасть под удар :)

Анимация: Fortnite / GIPHY
Раз уж мы заговорили о Fortnite, давайте попробуем разобрать основные компоненты игры на примере «Королевской битвы». Всего их шесть:
- Игроки: в каждом матче Fortnite участвует до 100 человек.
- Цель: остаться последним выжившим.
- Правила: участники начинают без снаряжения и должны искать оружие и ресурсы, в то время как карта постепенно сужается, чтобы принудить игроков к конфликту.
- Действия: можно строить структуры, собирать ресурсы, использовать оружие и предметы, а также перемещаться по карте.
- Информация: можно наблюдать, как другие игроки перемещаются по карте, используют оружие, возводят сооружения и так далее.
- Взаимосвязанность решений: если игрок строит башню, это может служить сигналом для других игроков — привлечь их в локацию или, наоборот, отпугнуть.
Конечно, теория игр не сводится к одному только математическому описанию компьютерных игр. Под её действие попадают любые житейские ситуации, где есть какой-то конфликт интересов — от выбора фильма для совместного просмотра до переговоров о скидке с продавцом на «Авито».
Что такое стратегия
Согласно теории игр любое действие приводит нас к какому-то результату — но не всегда к такому, который нас устроит. Поэтому действия в играх необходимо оптимизировать — то есть разработать стратегию.
Стратегия — это план действий, который учитывает все возможные ситуации в любой момент игры. При выборе стратегии принимают в расчёт ресурсы и возможные решения других игроков. Большинство стратегий заточены на максимизацию выигрыша — иначе зачем это всё?
Выигрыш — это то, что получает игрок в зависимости от того, какие действия он совершал. Если игрок принимал «хорошие» решения, ему достанется большой выигрыш, а если «плохие» — то небольшой или его не будет вовсе.
Например, если вы хотите одержать победу в шахматном поединке, сразу отдать ферзя противнику будет не лучшей стратегией. Гораздо эффективнее, если во время игры мы будем нападать на фигуры соперника и пытаться поставить шах королю. А если вдруг мы и потеряем ферзя, то попробуем продвинуть пешку до конца доски, чтобы его вернуть.
Анимация: Skillbox Media
В зависимости от целей, ресурсов и действий других игроков, стратегии в теории игр делятся на четыре основных типа:
- Чистая — игрок чётко знает, каким образом продолжит игру.
- Смешанная — игрок выбирает одну из чистых стратегий в зависимости от вероятности того или иного развития событий.
- Доминирующая — приводит к лучшему возможному результату для игрока, независимо от того, какие стратегии выбирают соперники.
- Компромиссная — используется в ситуациях, когда нет чёткого выигрыша или проигрыша. Вместо этого игроки могут искать компромисс, который позволит им достичь своих целей.
Чтобы выяснить, как выбор стратегии влияет на результат, разберём классическую ситуацию из теории игр, которая называется дилеммой заключённого.
Дилемма заключённого
Ситуация: двух преступников привели на допрос и содержат в разных камерах — они не могут разговаривать друг с другом. У следствия есть доказательства, чтобы обвинить их по незначительному преступлению, но нет улик, чтобы выдвинуть обвинение по более крупному делу.
Поэтому следствие предлагает преступникам сделку:
- Если оба преступника молчат и не сдают друг друга, то каждый из них получит небольшой срок за незначительное преступление — 2 года.
- Если один из них сдаст другого, а другой промолчит, то стукача отпустят на свободу, а второго посадят на 10 лет.
- Если оба сдают друг друга, то им грозит средний срок, но больше, чем если бы оба промолчали, — 5 лет.
На первый взгляд кажется, что лучшей стратегией было бы промолчать — ведь тогда оба преступника получили бы всего по два года. Но так как игроки не могут пообщаться друг с другом, появляются риски: если не дать показания, можно сесть в тюрьму либо на два года, либо на десять.
Поэтому лучшим выходом в этой игре будет… дать показания. Говоря формально, использовать доминирующую стратегию — то есть действовать в своих интересах и не думать о другом игроке. В этом случае можно либо выйти на свободу, либо получить пять лет, что вдвое меньше максимального срока.
Эту игру можно визуализировать в виде платёжной матрицы — таблицы, в которую заносят выигрыши каждого игрока в зависимости от его действий. Есть и другие способы математически представить игру — но нам пока хватит и этого.
| | Игрок 1 сознаётся | Игрок 1 молчит |
|---|---|---|
| Игрок 2 сознаётся | -5; -5 | -10; 0 |
| Игрок 2 молчит | 0; -10 | -2; -2 |
Ситуация, когда две доминирующие стратегии уравновешивают друг друга, называется равновесием Нэша. Того самого Нэша, про которого сняли фильм «Игры разума» с Расселом Кроу и который в целом является одним из основателей современной теории игр. Звучит этот принцип так:
Допустим, в игре есть несколько стратегий, которые приводят к определённым результатам. Но не все они эффективны для всех участников. Поэтому игроки могут найти такие стратегии, которые будут удовлетворять сразу всех игроков, хотя выигрыш может быть не максимальным.
Равновесие Нэша учит нас тому, что не стоит отклоняться от выгодной стратегии, если вы не знаете, как поведёт себя ваш оппонент, — пускай даже ваши действия будут максимально эгоистичными.
Какие бывают игры
Со стратегиями теории игр разобрались — теперь давайте расскажем об основных видах непосредственно игр. Всего их десять.
1️⃣ Кооперативные и некооперативные. В кооперативной игре участники могут объединяться в группы, чтобы достигать своих целей. Пример: Minecraft — в этой игре можно совместно исследовать мир и строить сооружения.
В некооперативных играх участники соревнуются друг с другом и никак не сотрудничают. Примеры — автогонки, шахматы.
2️⃣ С нулевой и ненулевой суммой. В играх с нулевой суммой один игрок забирает весь выигрыш, а проигравший — теряет всё. Примеры таких игр — покер, а также спортивные игры на выбывание.
Игры с ненулевой суммой — это те, в которых выигрыш можно распределить между разными игроками. Но самый успешный игрок всё равно получает больше остальных. И если один игрок потеряет часть выигрыша, то игра для него не закончится. Примеры: Civilization, Mount & Blade 2.
3️⃣ Параллельные и последовательные. В параллельных играх участники ходят или одновременно, или вслепую — то есть не знают, какое действие сделал соперник до тех пор, пока ход не закончится. Примеры: «Мафия» или та же самая дилемма заключённых.
Последовательные игры — это игры, в которых игроки ходят по очереди. Пример: шахматы.
4️⃣ С полной или неполной информацией. В первом случае игрок обладает всей информацией о действиях соперника, а во втором — либо не владеет ей вовсе, либо обладает только частью.
Полная информация есть в шахматах, а игры с неполной информацией — это, к примеру, онлайн-шутеры CS:GO или Call of Duty: Warzone.
5️⃣ Симметричные и несимметричные. Симметричные игры — это такие, в которых у всех игроков одинаковый набор стратегий, и если поменять их местами, конечный результат не изменится. Пример — дилемма заключённого.
В несимметричных играх стратегии у игроков могут быть разные.
Где применяется теория игр
Теорию игр можно использовать для моделирования практически любой ситуации — вплоть до самой бытовой. Давайте перечислим основные области, где её принципы используют уже сегодня:
- Бизнес — для анализа действий конкурентов и создания маркетинговой стратегии. Причём конкурентом может быть сама природа — например, если вы продаёте кроссовки и думаете, как сохранить размер выручки при любой погоде.
- Биология — для изучения поведения животных: как соперничество или, наоборот, объединение в группы помогает им выживать. Если обобщить — как сама эволюция строит оптимальные стратегии.
- Международные отношения — здесь это вообще один из основных инструментов. Например, теория игр помогает предсказать, как падение режима в стране повлияет на обстановку у соседей.
- Data science — для обучения нейросетей, которые взаимодействуют с людьми и другими ИИ. Например, нейронка от DeepMind научилась играть в «Захват флага» в процессе игры с людьми и машинами.
- Жизнь. Мы сами постоянно сталкиваемся с теорией игр, даже не осознавая этого. Пробки, выбор фильма на вечер, поход на свидание, совместное воспитание детей, переговоры о зарплате — все эти ситуации поддаются математическому моделированию.
Что почитать
В этой статье мы затронули только базовые определения из теории игр: понятие игры, игроков, действий и стратегий — но это только начало. Если хотите лучше разобраться в теории игр и научиться решать с её помощью сложные задачи, вот несколько ресурсов, где можно изучить тему поглубже:
- Видеолекции математика Алексея Савватеева.
- Бесплатный стэнфордский курс на Coursera.
- Б. Нейлбафф, А. Диксит, «Теория игр. Искусство стратегического мышления в бизнесе и жизни».
- Э. Гура, М. Машлер, «Экскурс в теорию игр. Нетипичные математические сюжеты».
- А. Диксит, С. Скит, Д. Рейли, «Стратегические игры».





