Что такое натуральные числа и как они устроены
Определение, свойства, примеры — погружаемся в основы математики.

Натуральные числа стали первой математической системой, которая заложила основу современной арифметики. Уже в 3000 году до н. э. древние египтяне использовали их для измерения полей и подсчёта урожая. В их записях каждому числу соответствовал свой символ: вертикальная палочка обозначала единицу, подкова — десятку, а свёрнутая верёвка — сотню.
Но что такое натуральные числа? Давайте в этом разберёмся: познакомимся с их свойствами, изучим особенности, а в конце — немного попрактикуемся с натуральными числами и напишем немного кода на языке JavaScript.
Содержание
- Понятие и определение натурального числа
- Количественный смысл натуральных чисел
- Свойства натуральных чисел
- Разряды натурального числа
- Практика с натуральными числами
Понятие и определение натурального числа
Натуральное число — это число, которое возникает при естественном счёте предметов. Например, при пересчёте яблок в корзине или книг на полке вы будете использовать натуральные числа: одно яблоко, два, три и так далее.
Единица считается минимальным натуральным числом, а ноль к таким числам не относится. Максимального натурального числа не существует, поскольку к любому такому числу вы всегда можете прибавить единицу и получить следующее большее: 999, 1000, 1001 … и так до бесконечности.

Читайте также:
Положительные числа от единицы до бесконечности образуют множество натуральных чисел, которое обозначается буквой N. Это множество служит основой для построения всех остальных числовых множеств в математике:
- Целые числа (Z) — расширение множества натуральных чисел, которое включает отрицательные числа и ноль: … , −3, −2, −1, 0, 1, 2, 3, …
- Рациональные числа (Q) — все числа, которые можно записать как отношение двух целых чисел (дробь): ½, ¾, −5/2.
- Иррациональные числа (I) — бесконечные непериодические десятичные дроби, которые невозможно представить в виде отношения целых чисел.
- Действительные числа (R) — это всё, что можно отметить точкой на числовой прямой (включая рациональные и иррациональные числа).
- Комплексные числа (C) — это числа вида a + bi, где a и b — действительные числа, а i — мнимая единица. Например: 2 + 3i, −1 + i.
Множество не следует путать с натуральным рядом чисел. Множество — это набор натуральных чисел, в котором порядок не имеет значения. Например, {3, 1, 4, 2} и {1, 2, 3, 4} — это одно и то же множество. В натуральном ряду числа всегда идут последовательно и упорядочены по возрастанию: 1, 2, 3, 4, 5…
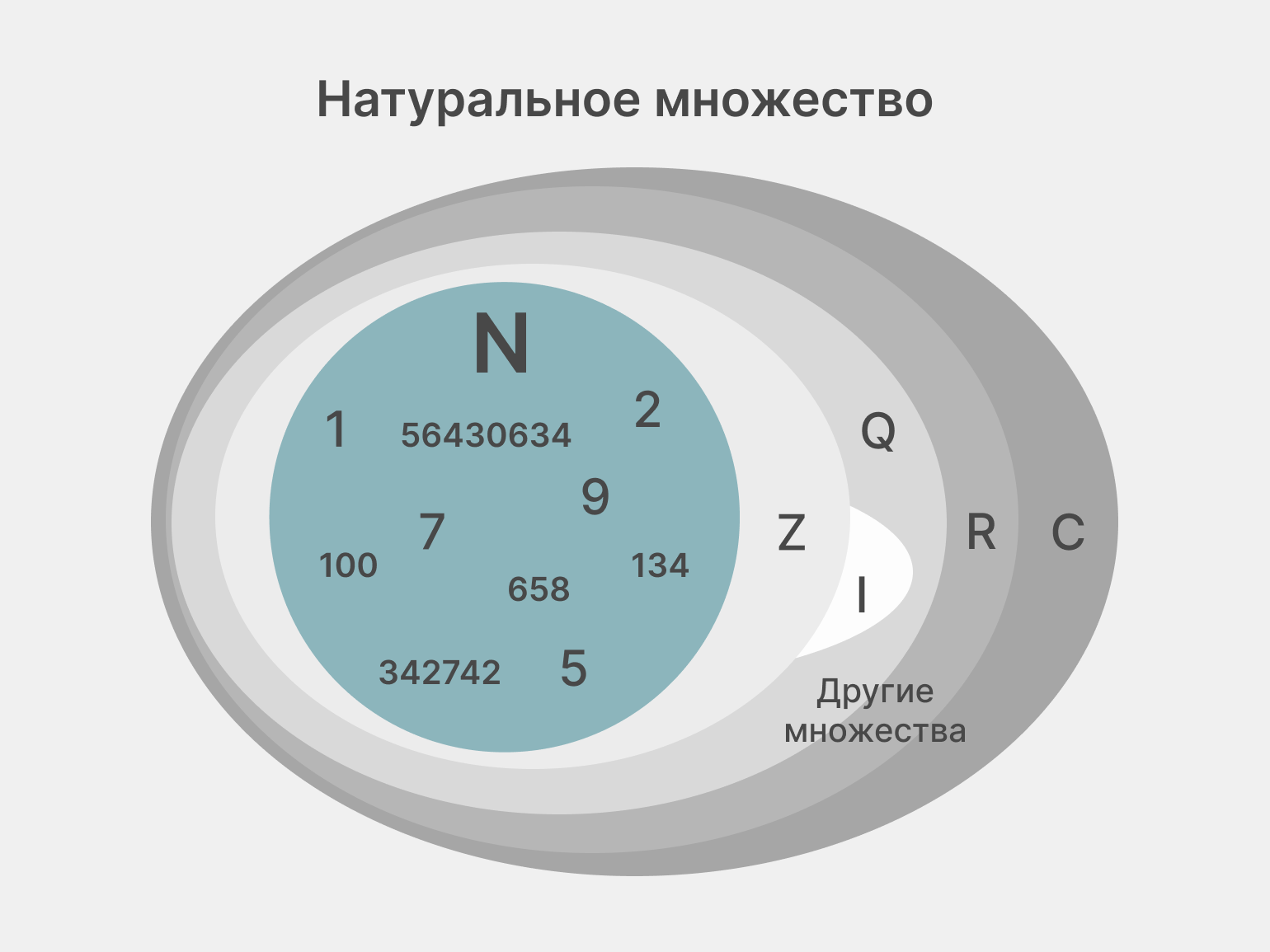
Инфографика: Skillbox Media
⚠️ Есть ещё один подход к определению натуральных чисел, который включает ноль в их множество. Это связано с разными взглядами математиков на природу нуля: одни не считают его ни положительным, ни отрицательным числом, а другие вовсе не рассматривают его как число. Поэтому в математической записи множество с нулём обозначается как N₀.
Количественный смысл натуральных чисел
Количественный смысл натурального числа заключается в том, что оно выражает целое количество реальных объектов в окружающем мире. Вы можете показать на руках три пальца, но не можете показать ноль пальцев или их отрицательное количество — это просто физически невозможно.
Количественный принцип применим к любым предметам, которые можно сосчитать: звёздочкам, камешкам, деревьям, книгам и чему угодно другому.

Инфографика: Skillbox Media
Возьмём пример с матрицами из математики. Матрица — это объект со строками и столбцами, похожий на страницу в клетку из тетради. У каждой строки и каждого столбца матрицы есть свой порядковый номер, причём их индексация начинается с единицы. Таким образом, номер любой ячейки строки или столбца матрицы всегда будет натуральным числом.
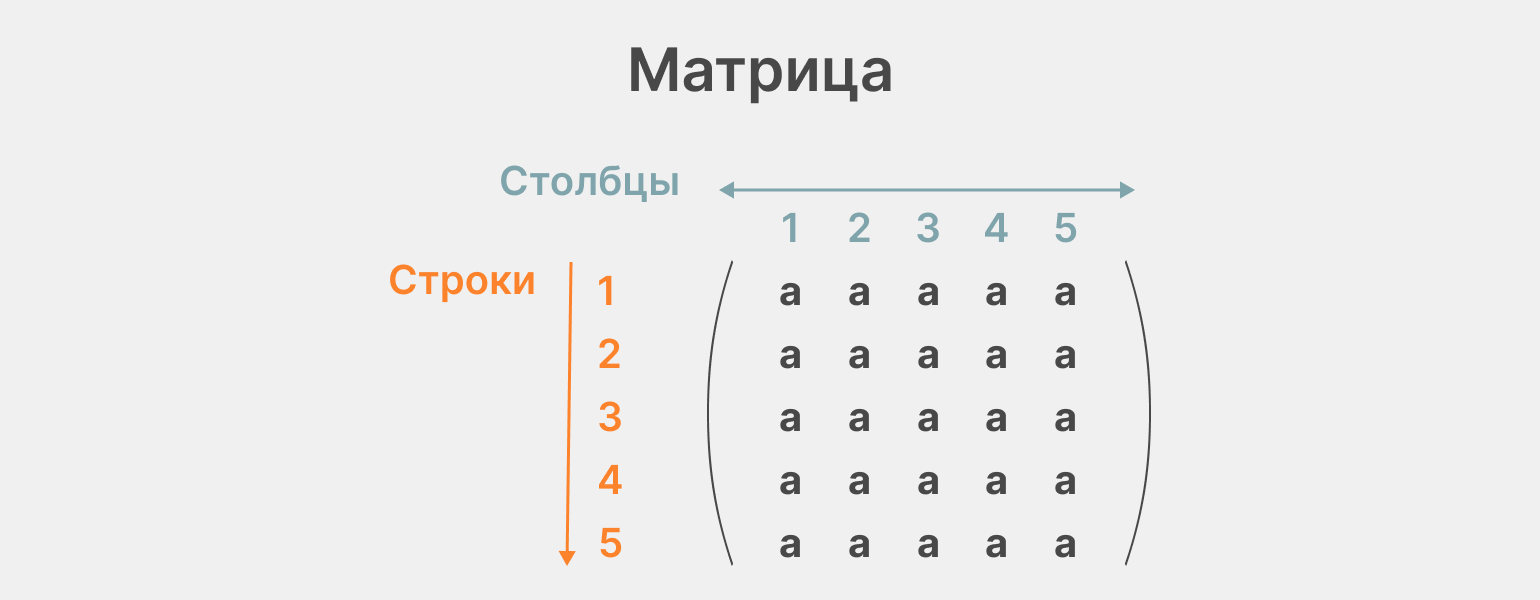
Инфографика: Skillbox Media
Массивы в программировании похожи на матрицы, но имеют важное отличие: нумерация их ячеек начинается с нуля. И хотя ноль не относится к натуральным числам, физически массив всегда начинается с первого элемента (с индексом 0) и не может иметь отрицательную длину. При этом длина массива обычно выражается натуральным числом.
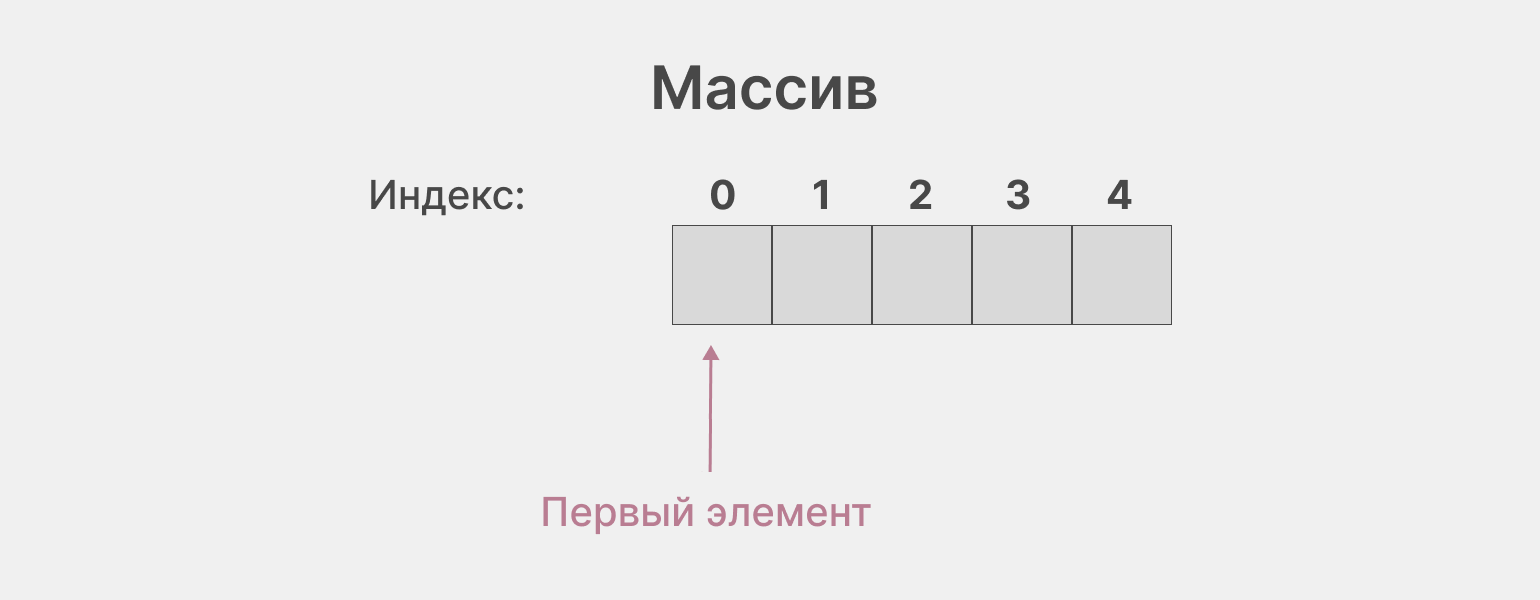
Инфографика: Skillbox Media
Свойства натуральных чисел
Вы уже знаете, что все натуральные числа положительны, начинаются с единицы и никогда не заканчиваются. Однако у них есть и другие свойства:
- При сложении и умножении натуральных чисел всегда получается натуральное число. Например: 5 + 3 = 8, 4 × 6 = 24.
- При делении любого натурального числа на единицу результат равен самому числу (8 ÷ 1 = 8). Если разделить натуральное число на само себя, всегда получится единица (8 ÷ 8 = 1).
- Переставляя местами числа при сложении или умножении, мы получим тот же самый результат 2 + 3 = 3 + 2 = 5, 2 × 4 = 4 × 2 = 8.
- Результат сложения или умножения не зависит от порядка действий с числами. Пример: (2 + 3) + 4 = 2 + (3 + 4) = 9, (2 × 3) × 4 = 2 × (3 × 4) = 24.
- Если мы вычитаем из меньшего числа большее (3 − 5 = −2), то получаем отрицательное целое число, которое не является натуральным числом.
- Умножение числа на сумму равно сумме произведений этого числа на каждое слагаемое. Проще говоря: 2 × (3 + 4) = (2 × 3) + (2 × 4) = 6 + 8 = 14.
- При умножении любого числа на ноль результат всегда равен нулю (5 × 0 = 0), причём сам ноль не является натуральным числом.
- Любое натуральное число можно представить как сумму единиц. Например, 4 = 1 + 1 + 1 + 1.
- Натуральные числа можно сравнивать между собой: одно число всегда будет больше (5 > 3), меньше (2 < 7) или равно (4 = 4) другому.
Разряды натурального числа
Каждое натуральное число состоит из разрядов. Разряд показывает позицию цифры в числе, если считать справа налево. Возьмём число 425: в первом разряде стоит цифра 5, во втором — 2, а в третьем — цифра 4.
У разрядов есть порядковый номер и название: единицы, десятки, сотни, тысячи и так далее. Крайний левый разряд называется старшим, а крайний правый — младшим. Разберём для примера выбранное число 425: первый разряд (5) — это единицы, второй (2) — десятки, третий (4) — сотни. Получается, старший разряд здесь — сотни (4), а младший — единицы (5).
В программировании при работе с битами также используются понятия старшего и младшего бита. Например, в двоичном числе 10100010 самая левая единица — старший бит, а крайний правый ноль — младший бит.

Инфографика: Skillbox Media
Натуральные числа можно классифицировать по их длине: однозначное число — с одним разрядом, двузначное — с двумя, трёхзначное — с тремя, и так по возрастанию. При этом число с четырьмя и более разрядами называется многозначным. Например, число 1234 — это четырёхзначное многозначное число, а число 12345 — пятизначное многозначное число.
Чтобы легче читать большие числа, разряды объединяют в классы. Каждый класс состоит из трёх разрядов. Для наглядности разберём число 123 456 789. В нём три класса: класс единиц (789), класс тысяч (456) и класс миллионов (123). Затем идут классы миллиардов, триллионов и другие. Такое деление помогает лучше понимать структуру больших чисел.
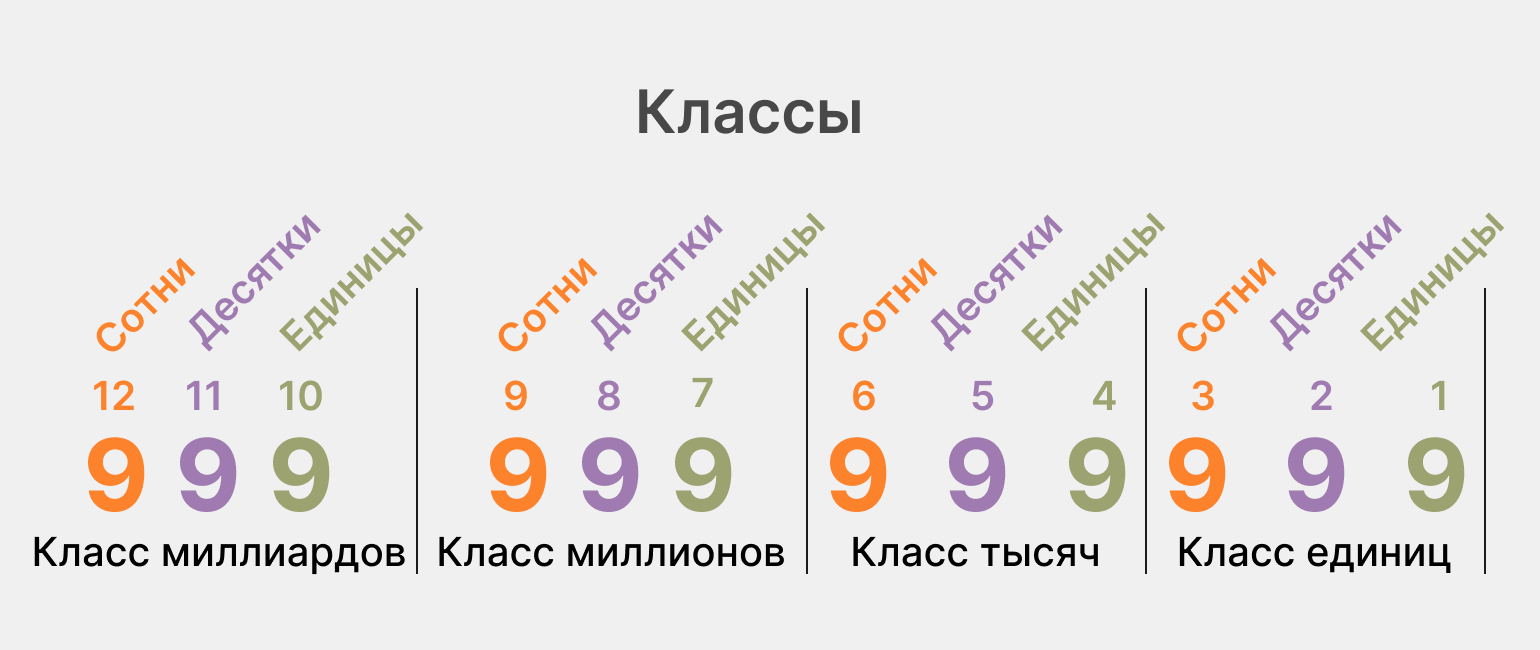
Инфографика: Skillbox Media
Практика с натуральными числами на JavaScript
В этом разделе мы создадим массив, заполним его произвольным количеством натуральных чисел и посчитаем их сумму.
Для начала откройте консоль браузера и приготовьтесь писать код. Не переживайте, если вам что-то непонятно — просто повторяйте и смотрите результат. Немного практики, и JavaScript перестанет казаться загадкой.
Создадим массив и наполним его произвольным количеством чисел:
let naturalNumbers = [1, 5, 8, 12, 15];Посмотрим длину массива:
console.log(naturalNumbers.length); // 5Теперь создадим функцию и заполним наш массив случайными числами:
function fillArray(arr, count) {
for(let i = 0; i < count; i++) {
arr.push(Math.floor(Math.random() * 100) + 1);
}
return arr;
}
naturalNumbers = fillArray(naturalNumbers, 15);
console.log(naturalNumbers);Посмотрим длину обновлённого массива:
console.log(naturalNumbers.length); // 20Осталось посчитать сумму натуральных чисел и вывести результат:
const naturalNumbersSum = naturalNumbers.reduce((acc, curr) => acc + curr, 0);
console.log(`Сумма всех чисел массива: ${naturalNumbersSum}`);В нашем примере сумма всех натуральных чисел массива составила 726. Попробуйте запустить код и узнайте, какой результат получится у вас! 🤔
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!