Числа с плавающей точкой: что это такое и как они работают
Рассказываем, как дробные числа хранятся в памяти компьютера — всё сложно и волшебно, но оправданно.


Компьютеры придумали, чтобы производить вычисления более точно и быстро. Но парадокс в том, что на самом деле их вычисления почти всегда неточны. Например, мы не можем представить число Пи или корень из двух в памяти компьютера — потому что имеем дело с бесконечной дробью (хотя и с «короткими» числами всё не так просто из-за двоичной системы счисления, в которой числа представлены в памяти компьютера, к этому мы тоже вернёмся).
Так что компьютер в какой-то момент идёт на уступки и ограничивается вычислениями с той точностью, которая необходима для решения стоящей за ними практической задачи.
Чтобы эффективно проводить вычисления, учёные придумали числа с плавающей точкой — они стали отличным инструментом для представления вещественных чисел (это, по сути, все числа числового ряда, даже те, у которых дробная часть бесконечна).
Под числа с плавающей точкой даже создан единый стандарт IEEE 754 — чтобы все компьютеры, языки программирования, программы и операционные системы работали с ними одинаково и результат получался предсказуемым. В этой статье мы расскажем, что это за стандарт и как он работает.
Кто придумал числа с плавающей точкой
1970-е годы, начало компьютерной революции. Учёные-программисты разрабатывают новые компьютеры и алгоритмы для вычислений, а также стараются всеми силами доказать, что их изобретения должны изменить мир.
Тогда все компьютеры работали по-разному: у них были собственные операционные системы, принципы организации памяти и способы представления данных. И это создавало проблему: нельзя было перенести программу с одного компьютера на другой, для этого каждый раз приходилось переписывать её под новую систему и «железо».
И если переделать пару функций было не так сложно, то подстраиваться под разные системы представления чисел было действительно мукой. Из-за этого иногда нужно было полностью менять поведение программы, что могло повлиять на её работоспособность и надёжность. В общем — проблема с представлениями чисел была поистине болезненной.

Фото: Wikimedia Commons
Компания Intel решила помочь программистам со всего мира и создать единый стандарт представления вещественных чисел. Для этого была создана проектная группа из лучших инженеров. Но на пятки Intel наступали и другие компании — например, у той же DEC появилась похожая идея.
Началась настоящая гонка за лучшее решение: каждая компания фанатела исключительно от своей разработки и надеялась, что именно её примут как промышленный стандарт. А IT-гиганты IBM и Cray наблюдали за всем происходящим со стороны и ждали, пока появится победитель, — чтобы тут же реализовать его стандарт в своих компьютерах.
Сегодня из всех стандартов, возникших в то время, в живых остались только два: спецификация VAX от DEC и K-C-S от Intel. У каждой из них были как свои преимущества, так и недостатки.
Преимущества K-C-S:
- Десятичный формат. Он позволял представлять вещественные числа в десятичной записи, что очень удобно для человека, но так себе для компьютера.
- Высокая точность. Десятичное представление повышало точность вычислений и снижало возникновение ошибок при округлении — особенно для операций с большими числами.
- Меньше ошибок. Стандарт включал специальные значения, которые помогали легко избегать переполнения чисел и проще справляться с ошибками при вычислениях.
Преимущества VAX:
- Двоичный формат. Все числа записывались только в двоичном представлении, что повышало эффективность вычислений, особенно на компьютерах с VAX-архитектурой.
- Широкое распространение. Спецификацию VAX уже использовали на разных компьютерах того времени, что позволяло быстро адаптировать её под новые устройства.
- Высокая производительность. Спецификация VAX была оптимизирована под высокую скорость работы и требовала меньших вычислительных мощностей.
| K-C-S | VAX |
|---|---|
| Десятичный формат | Двоичный формат |
| Высокая точность | Высокая производительность |
| Меньше ошибок | Широкая распространённость |
Компания DEC пыталась сделать всё, чтобы VAX признали единым стандартом. Она даже пыталась убедить авторитетных учёных в том, что конкурирующий K-C-S никогда не станет таким же производительным и успешным. Однако у разработчиков из Intel были свои секретики: например, они знали, как ускорить свою спецификацию и обогнать DEC.
В итоге победила Intel, а её спецификация легла в основу стандарта IEEE 754, который утвердил Институт инженеров электротехники и электроники (IEEE) в 1985 году.
Что такое фиксированная точка
Чтобы понять стандарт IEEE 754, нам нужно сперва разобраться, как числа представляют в двоичной системе. Всего существует два представления десятичных чисел в компьютере: с плавающей точкой и фиксированной. Первые основаны на вторых, поэтому есть смысл начать с них.
И да, дальше мы будем употреблять слово «точка», однако в других статьях и литературе можно встретить термин «запятая». Они означают одно и то же, но в англоговорящих странах чаще используют второй, а в русскоговорящих — первый.
Числа с фиксированной точкой — это двоичные числа, у которых ограничен размер их целой и дробной части. Например, если число состоит из 16 битов, то мы можем выделить для целой части первые 10 битов и оставшиеся шесть — для дробной части.
Разделение между целой и дробной частью как раз и обозначают точкой. Когда компьютер получает число, он сразу понимает, что в нём 2 байта, или 16 битов, из которых 10 — это целая часть, а шесть — дробная. Получится так:

На картинке — двоичное представление десятичного числа 689.6875 в виде двоичного числа с фиксированной точкой. Вот ещё один пример с числом поменьше:

Здесь закодировано число 13.0. Видим, что в дробной части одни нули и, соответственно, дробная часть десятичного числа — нулевая.
Давайте подробнее разберём, почему всё получилось именно так. Сначала посмотрим на целую часть — это обычное представление десятичного числа в двоичной записи. Каждый разряд числа относится к степени двойки. Число из примера выше можно разложить так:
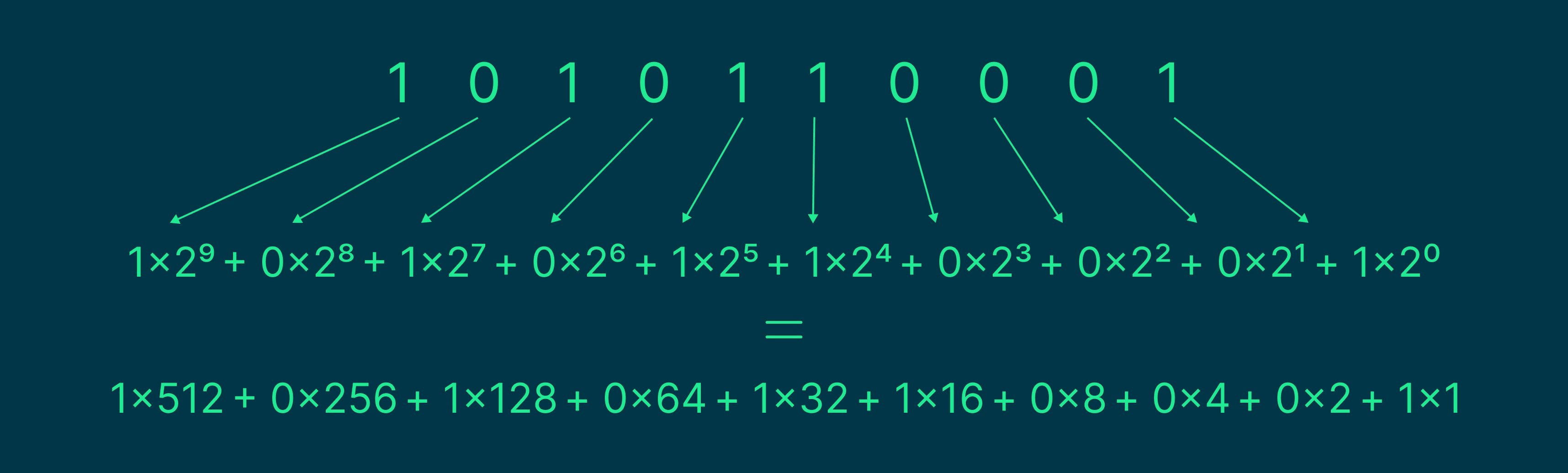
Чтобы перевести двоичную запись в десятичную, нужно сложить все степени двойки, у которых в разряде стоит единица. Получим:

Теперь рассмотрим дробную часть. Принцип перевода дробной части двоичного числа в десятичную систему такой же. Единственное отличие в том, что там степени двойки — отрицательные. Рассмотрим число из примера выше:

Степень двойки начинается с −1 и с каждым разрядом уменьшается на единицу: −2, −3 и так далее, а чтобы перевести её из отрицательной в положительную, нужно просто перевернуть дробь. И теперь мы также складываем все степени двойки, у которых в соответствующем разряде стоит единица:

Теперь нам осталось сложить целую часть с дробной:

Преимущества чисел с фиксированной точкой в том, что они всегда представляются в виде конечного числа. Это значит, что если мы захотим представить число Пи, то оно будет ограничено на определённом знаке, а остальные мы просто отбросим. Например, так:

Это число — приближённое представление числа Пи, и оно не является его точным значением.
Недостатки у чисел с фиксированной точкой, конечно же, тоже есть. Например, если мы возьмём 16-битные числа, у которых первые 10 битов относятся к целой части и остальные шесть — к дробной, то в нашем распоряжении окажется такой диапазон значений:

И тут мы переходим к главному недостатку чисел с фиксированной точкой. Давайте возьмём самое большое число, которое можно записать таким образом, и вычислим число перед ним, то есть такое число:

Видим интересное: когда мы убрали одну единицу в конце двоичного числа, то получили разницу между двумя числами не 0.000001, как в десятичных числах, а 0.015625. Это число представляет собой как бы минимальный шаг в числах с фиксированной точкой, или максимально возможную точность.
Если мы возьмём следующее число, то разница останется такой же:

Эта точность, во-первых, позволяет превращать десятичные числа в двоичные, а во-вторых, уменьшает нагрузку на компьютер, ведь компьютер всегда знает, что первые 10 битов — это целая часть, а оставшиеся шесть — дробная.
С фиксированной точкой разобрались, теперь перейдём к плавающей, а затем узнаем уже о формате IEEE 754.
Что такое плавающая точка
Если говорить техническим языком, то число с плавающей точкой (или число с плавающей запятой) — это численное представление вещественного числа в программировании. Иначе говоря, оно является его приближённым значением.
Двоичное представление чисел с плавающей точкой содержит три части: знаковый бит, экспоненту и мантиссу.
- Знаковый бит указывает, положительное число или отрицательное.
- Экспонента показывает, на какое число нужно умножать мантиссу.
- Мантисса — это фиксированное количество битов, которое выражает точность числа.
Эти определения слегка сложноваты, поэтому давайте сначала разберёмся с основами.
В научной нотации числа удобнее представлять как что-то небольшое, умноженное на 10 в какой-то степени. Например, число 123.456 удобнее представить в виде 1.23456 × 102 Это удобнее, потому что для умножения двух чисел в таком виде не приходится тратить много сил. Звучит неочевидно, но давайте посмотрим на практике — умножим число 0.0006 на 0.0002:
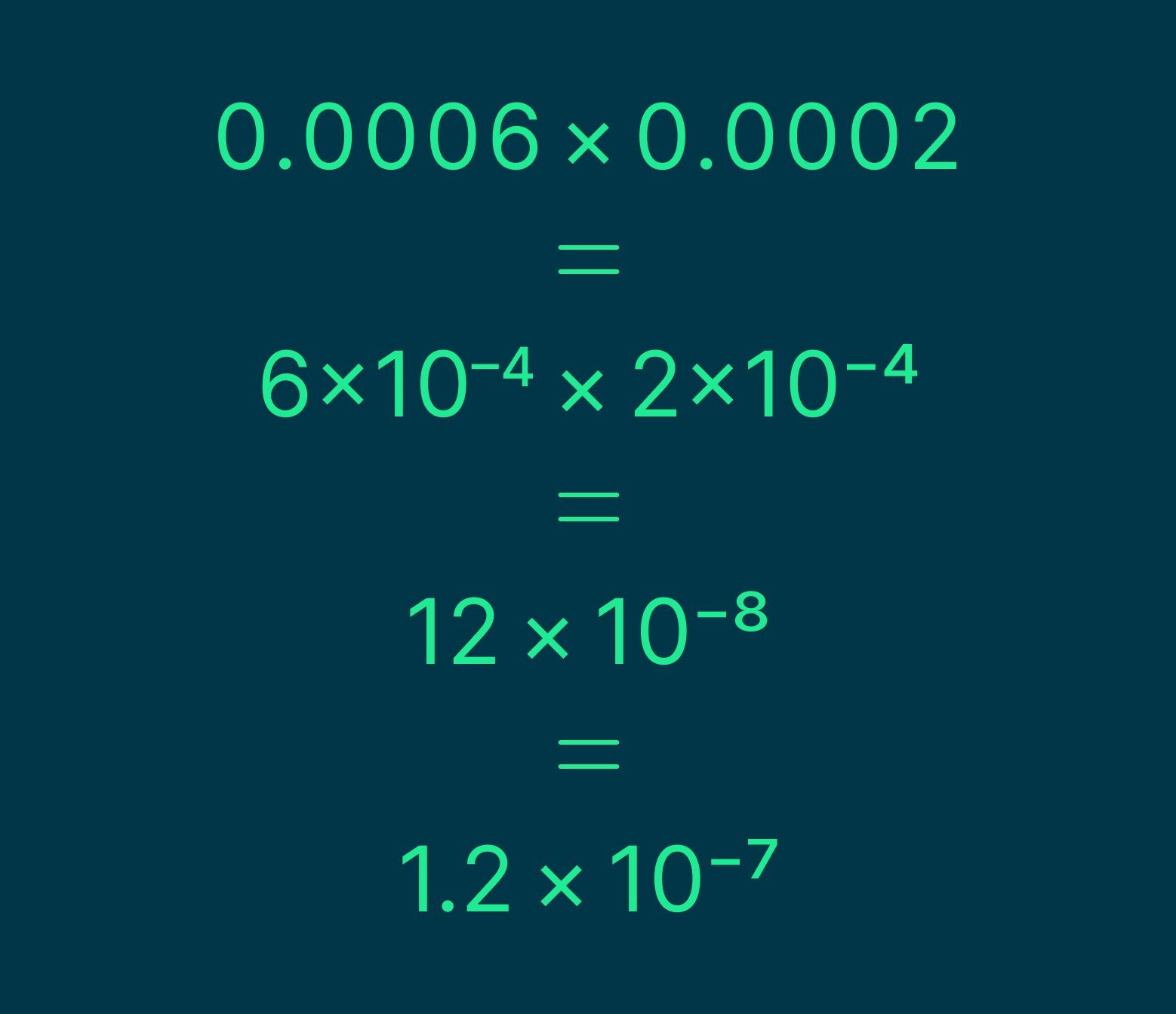
Как мы видим, в научной нотации нужно было просто сложить степени и произвести несложное умножение. А в обычном виде нам нужно было умножить два числа и ещё не запутаться, сколько нулей слева нужно дописывать. Одним словом — научная нотация проще.
В этой нотации число состоит тоже из трёх компонентов: экспоненты, коэффициента, мантиссы и знака числа.
- Знак числа указывает, какое это число: положительное или отрицательное. Он нужен, чтобы мы постоянно работали с положительным числом, а уже потом при необходимости перевели его в отрицательное.
- Коэффициент — это основная часть десятичного числа, записанного обычно в диапазоне от 1 до 9. Но для чисел с плавающей точкой он находится в диапазоне от 0 до 1.
- Мантисса — это дробная часть коэффициента.
- Экспонента — это то, на что мы умножаем коэффициент.
Так, число 1.2 × 10−7 можно представить следующим образом:

Вот что мы получили:
- +1 — знак числа (положительный),
- 0.12 — мантисса,
- −8 — экспонента.
Можно заметить, что мы сразу заменили коэффициент 1.2 на 0.12. Мантисса — 0.12.
Число 10 называют основанием. Принято использовать его, потому что мы считаем всё в десятичной системе. Однако основание можно и поменять. Давайте представим число 0.12 × 10−8 в виде числа с основанием 5.

Мантисса стала более устрашающей, но заметьте, что экспонента (то есть степень) не поменялась. И это абсолютно нормально, ведь мы применяли базовые правила умножения.
Почему не поменялась экспонента? Следите за руками :) Сначала мы разбиваем число 10 на множители — 5 и 2, а раз у исходного числа была степень −8, то у нас будут множители 5−8 и 2−8.
Теперь давайте перейдём к двоичному представлению. В нём основанием будет число 2, потому что это эквивалент числу 10 в двоичной системе. А мантисса будет точно так же лежать в диапазоне от 0 до 1 (не включительно). Поэтому всё, что меняется, — это основание.
Выглядеть десятичное число 0.12 × 10−8 в двоичном представлении будет вот так:
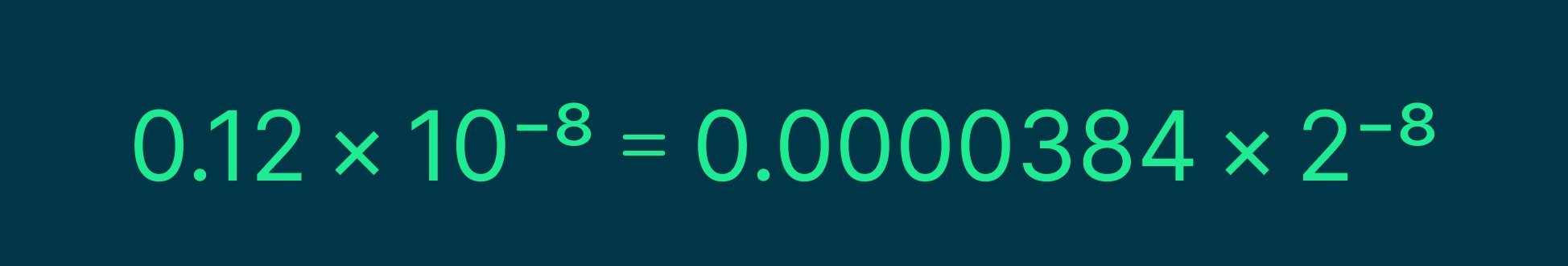
Научная нотация — это тот принцип, по которому строится двоичное представление десятичных чисел в компьютерах. Теперь давайте разбираться, что за стандарт IEEE 754 и как он работает.
Как представляют числа с плавающей точкой
Стандарт IEEE 754 — это набор правил, которые описывают, как вещественные числа представляются в компьютере. Этот формат стал самым распространённым в программировании, когда дело доходит до арифметики чисел с плавающей точкой.
Числа представляются фиксированным количеством битов, каждый из которых отвечает своим задачам. В IEEE 754 обычно используют 32 бита. Они делятся на всё те же категории: один знаковый бит, 7 битов для экспоненты (то, на что мы умножаем мантиссу) и 24 бита для мантиссы (она выражает точность числа).

Чтобы получить из этого представления десятичное число, используют следующую формулу:
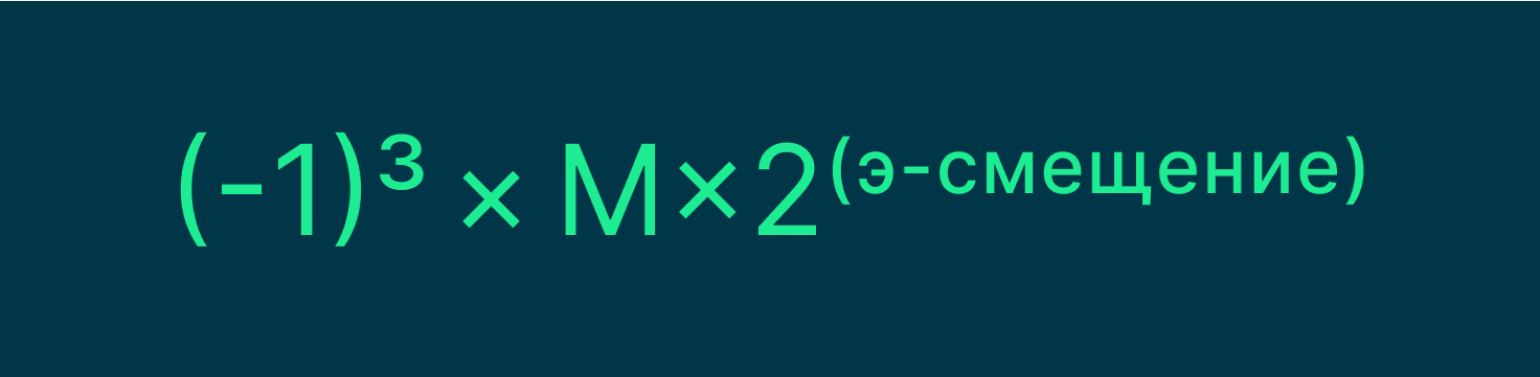
Здесь З — это знаковый бит, М — мантисса, Э — экспонента. А ещё у нас появилось смещение. Оно необходимо, чтобы экспонента могла принимать положительные и отрицательные значения, и в стандарте IEEE 754 представляет собой константу — число 127.
Если без смещения экспонента может принимать значения от 0 до 255, то со смещением от −127 до 128. Это нужно, чтобы представлять маленькие числа.
Чтобы вычислить мантиссу, мы должны добавить к ней слева единицу и после неё поставить точку, как будто это число с фиксированной точкой. А затем вычислить это число:
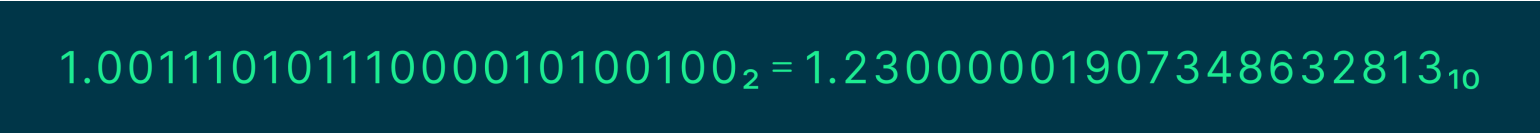
Получили наше число 1.23, но не совсем. То, что вы видите, называется приближением двоичных чисел к десятичным. Если бы у нас было бесконечное количество битов, то мы смогли бы довольно точно представить число 1.23 в двоичной системе, и оно получило бы вид: 1.2300000000000000000000000000000001. Что уже неплохое приближение. Но так как у нас ограниченное число битов, приходится идти на округление.
Теперь давайте подставим все числа в формулу:

Всё сходится. Попробуем перевести ещё одно число в десятичную систему. На этот раз двоичное число будет таким:
0 10000000 11100000000000000000000
Пройдём все те же шаги:
- знаковый бит — 0;
- экспонента — 128;
- мантисса — 1.875.
Теперь подставляем в формулу:

Получили число 3.75 в десятичной записи.
Какие особенности у чисел с плавающей точкой
Мы узнали, как числа с плавающей точкой хранятся в памяти компьютера, какие биты за что отвечают и как происходит преобразование из стандарта IEEE 754 в десятичные числа. Теперь давайте узнаем, какие у них есть нюансы, о которых точно нужно знать.
Специальные числа: ноль, бесконечность и неопределённость
Числа с плавающей точкой имеют два нуля (положительный и отрицательный), две бесконечности (положительную и отрицательную) и неопределённость. И всё это нужно, чтобы правильнее считать числа.
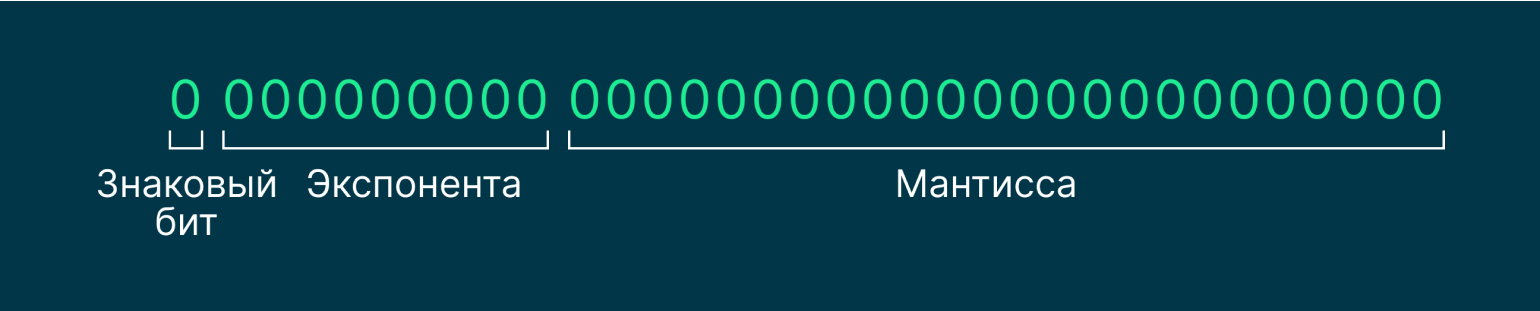
Два нуля. В стандарте IEEE 754 существуют два нуля — положительный и отрицательный. Они нужны, чтобы компьютер мог различать значения, которые близки к нулю, но имеющие разные знаки. Это важно при умножении и делении.
Например, представьте, что у банка есть финансовое приложение, которое работает с очень маленькими процентными ставками, такими как 10−15. Если бы у нас не было двух нулей, то при округлении мы бы получали неточные значения. Мы бы не смогли знать, отрицательная ставка у клиента или положительная, а это бы влияло на то, сколько он будет платить денег, что очень важно для него.
В стандарте IEEE 754 эти два нуля записываются так:
Изображение: Skillbox Media

Изображение: Skillbox Media
Экспонента и мантисса должны содержать все нули, а знаковый бит будет указывать, какой мы имеем ноль: положительный или отрицательный.
Две бесконечности. Они напрямую связаны с двумя нулями. На уроках математики вам могли говорить, что делить на ноль нельзя, но это не совсем так. Делить на ноль можно, просто мы будем получать бесконечность, с которой не очень удобно работать.
У бесконечности есть два типа: положительная бесконечность и отрицательная бесконечность. Чтобы получить положительную, нужно положительное число поделить на положительный ноль или отрицательное число на отрицательный ноль:

Отрицательную бесконечность можно получить похожим образом, только если поделить отрицательное число на положительный ноль или положительное число на отрицательный ноль:

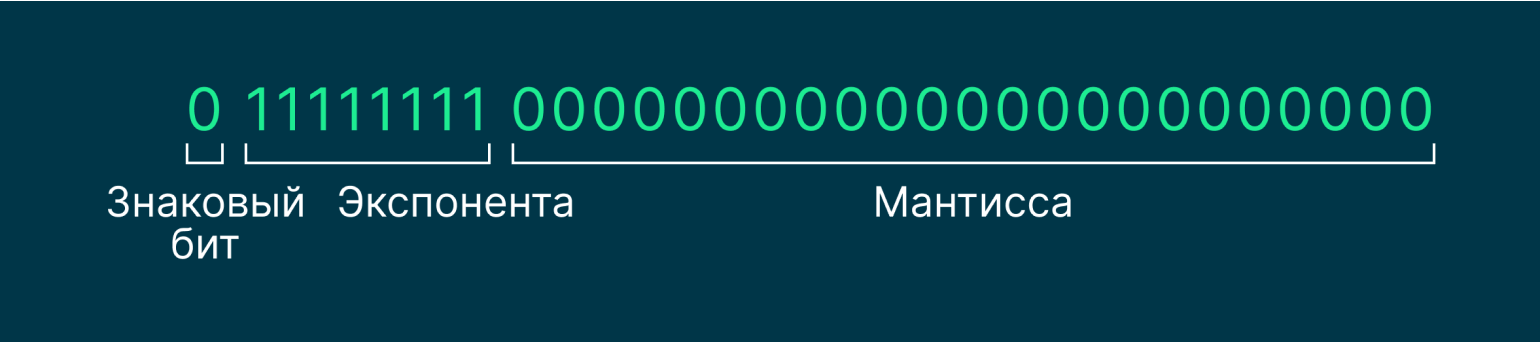
Чтобы понять, где и когда применяют бесконечности, нужно обращаться к математическому анализу, но это сложная тема, которую мы не будем затрагивать. Давайте просто посмотрим, как выглядят бесконечности в виде двоичной записи стандарта IEEE 754:
Изображение: Skillbox Media

Изображение: Skillbox Media
В бесконечностях экспонента всегда должна состоять из единиц, а мантисса — из нулей. При этом знаковый бит указывает, какая это бесконечность: положительная или отрицательная.
Неопределённость. В математике есть понятие неопределённости. Это когда мы делим что-то на что-то и не знаем, какой результат получили. Звучит странно: как это мы можем не знать результат? Но давайте на примерах.
Что мы получим, если поделим ноль на ноль, бесконечность на бесконечность, бесконечность на ноль или ноль на бесконечность? Никто не знает. Поэтому математики говорят, что мы получим неопределённость. А в стандарте IEEE 754 вводят понятие Not-a-Number — NaN. Выглядит оно так:

Неопределённость очень похожа на бесконечность, но главное её отличие в том, что в числе NaN должен быть хотя бы один ненулевой бит в мантиссе.
Нормализованные и денормализованные числа
Стандарт IEEE 754 поддерживает два вида вещественных чисел: нормализованные и денормализованные. Нормализованные числа нужны, чтобы представлять очень большие значения, а денормализованные — очень маленькие, которые близки к нулю.
Нормализованные числа. Они нужны, чтобы хранить и обрабатывать значения с максимально возможной точностью, что может быть критическим для некоторых приложений. Ещё для нормализованных чисел нужно меньше места в памяти.
Если говорить просто, нормализованные числа — это научная нотация чисел. Например, чтобы записать число 123 в научной нотации, нужно привести его к такому виду: 1.23 × 102. Это и будет нормализованным числом. В нём коэффициент (число 1.23) должен находиться в диапазоне от 1 до 9.
Чтобы отличать нормализованные числа, в стандарте IEEE 754 первый бит мантиссы делают равным единице. И тогда число принимает следующий вид:

Изображение: Skillbox Media
Удобство такого метода в том, что нам нужно хранить меньше битов в памяти, потому что первый бит мантиссы всегда равен единице. А также у нормализованных чисел гораздо больше диапазон значений.
Но при этом возникает другая проблема: если число близко к нулю, то мы не можем представить его с нужной нам точностью. Это число просто пропадёт из нашего вида, потому что компьютер округлит его до нуля. Поэтому работать с очень маленькими значениями в нормализованном виде не получится.
Денормализованные числа. Чтобы решить проблему округления при близких к нулю значениях, используют денормализованные числа. Они менее эффективны, так как нужно хранить больше битов в памяти, но при этом более точны.
Если коэффициент нормализованных чисел принимает значения от 1 до 9, то у денормализованных — от 0 до 1, не включая последнюю. А первый бит мантиссы у таких чисел всегда равен нулю. Поэтому двоичная запись будет выглядеть так:
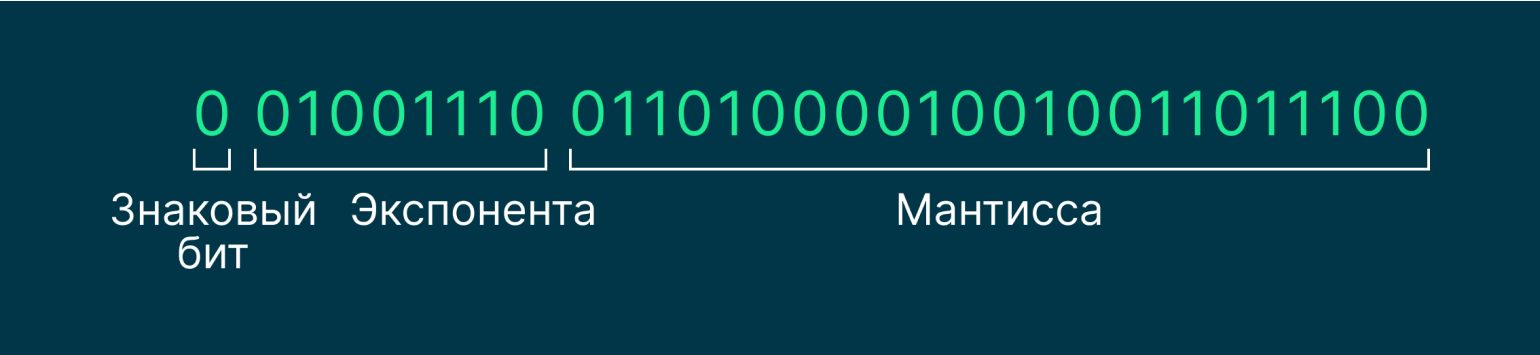
Изображение: Skillbox Media
Денормализованные числа могут привести к потерям в точности во время математических операций, что само по себе приводит к нестабильности вычислений — а это очень плохо.
Некоторые системы предпочитают обращаться с денормализованными числами очень просто: считать, что они все равны нулю. Другие — используют специальные способы обработки таких значений. Но все они неэффективны, потому что компьютеры сами по себе не умеют с ними взаимодействовать.
Интересно заметить, что граница между нормализованными и денормализованными числами лежит ровно на числе 0.75.
Числа одинарной и двойной точности
Выше мы рассматривали привычные числа с плавающей точкой. Они состоят из 32 битов: одного знакового бита, восьми для экспоненты и 23 для мантиссы. Этот стандарт называется одинарной точностью и является самым распространённым форматом среди вещественных чисел.
В разных языках программирования есть свои представления десятичных чисел, и в некоторых они суперточные. Например, в Java существуют типы BigInteger и BigDecimal, которые, по сути, не ограничивают размер числа. Такая переменная может хранить и 32 бита, и 302 бита. Но, конечно же, такой размах влияет на производительность, потому что хранятся эти числа как строки.
Одинарная точность может представить числа в диапазоне от −3.40282347 × 1038 до +3.40282347 × 1038. И сама точность составляет семь знаков после точки. Этот формат часто используют в компьютерной графике, научном моделировании и других приложениях, которым нужен баланс между диапазоном значений и точностью.
Кроме одинарной точности, есть ещё и двойная. Такие числа состоят из 64 битов, из которых один принадлежит знаку, 11 — экспоненте, 52 — мантиссе. Доступный диапазон значительно шире: от −1.7976931348623157 × 10308 до +1.7976931348623157 × 10308. А точность уже составляет 15–17 чисел после запятой.
Числа с двойной точностью используют там, где важна высокая точность. Например, их применяют для научных и инженерных вычислений, в которых допустить ошибку бывает критично. Но это всё усложняется большими ресурсными тратами — в памяти и компьютерных мощностях.
Что запомнить
Мы разобрали, как устроены и как работают числа с плавающей точкой. Это тема гораздо шире и глубже, а её изучение может занять не один день. Поэтому давайте подведём итог и перечислим, что можно вынести из этой статьи:
- Числа с плавающей точкой — это приближённое представление вещественных чисел в программировании. Все правила их представления записаны в стандарте IEEE 754.
- Этот стандарт нужен, чтобы разные компьютерные архитектуры могли одинаково удобно и эффективно работать с вещественными числами.
- Числа с плавающей точкой бывают с одинарной точностью и двойной. Числа с одинарной точностью состоят из 32 битов: одного знакового бита, восьми битов для экспоненты и 23 битов для мантиссы. Числа с двойной точностью — из 64 битов: одного знакового бита, 11 битов для экспоненты и 52 битов для мантиссы.
- В стандарте IEEE 754 есть специальные значения, которые нужны для представления положительного и отрицательного нуля, бесконечностей и неопределённости.
Больше интересного про код в нашем телеграм-канале. Подписывайтесь!






