Числа Фибоначчи: для чего нужны и почему так популярны
Их проходят почти на каждом курсе по программированию, но не объясняют, зачем они нужны. Пришло время в этом разобраться.


Тысячу лет назад люди увлекались вовсе не нейросетями, а числами и их свойствами. Так, в XII веке главным трендом были загадочные числа Фибоначчи, следы которых и сейчас можно найти практически везде: от расположения лепестков на дереве до формы ураганов и галактик.
Давайте узнаем, откуда появились эти числа, зачем они нужны и что нам с ними делать.
Что за числа Фибоначчи
Числа Фибоначчи — это последовательность чисел, которые задаются по определённому правилу. Оно звучит так: каждое следующее число равно сумме двух предыдущих. Первые два числа заданы сразу и равны 0 и 1.
Вот как выглядит последовательность Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, … , ∞
Длиться этот числовой ряд может бесконечно, но для большинства задач обычно хватает первых десяти чисел:
- первое — 0;
- второе — 1;
- третье — 1;
- четвёртое — 2;
- пятое — 3;
- шестое — 5;
- седьмое — 8;
- восьмое — 13;
- девятое — 21;
- десятое — 34.
Ну умеем мы складывать числа друг с другом, и что с того? Можно придумать ещё несколько таких же последовательностей — например, где следующее число будет равно сумме трёх или четёрых предыдущих. Как это пригодится в науке и технике? Но обо всём по порядку.
Для начала — заберёмся чуть глубже в историю.
Как появились числа Фибоначчи
Первым эту последовательность описал итальянский учёный Леонардо Пизанский по прозвищу Фибоначчи. Он жил в XII веке и усердно изучал работы античных и индийских математиков. В них Леонардо нашёл много полезных знаний — например, что десятичная система удобнее, чем римская нотация, и что по ней проще считать.

Изображение: I benefattori dell’umanita. L. Ducci e C., 1850 / National Library of Naples / Icas94 / DeAgostini / Getty Images
Полученные знания Леонардо систематизировал в своём главном труде — «Книге абака». Там же появилось и первое упоминание о числах Фибоначчи — как ни странно, в контексте решения задачи о кроликах:
Задача о размножении кроликов
В огороженный загон посадили двух кроликов — самку и самца. Каждый месяц пара являет миру ещё одну пару кроликов. Вопрос: сколько пар кроликов будет в загоне через год?
Конечно, решить эту задачу не так просто, потому что на размножение кроликов влияет много факторов — например, они могут умереть или убежать. Поэтому Леонардо ограничил задачу такими условиями:
- кролики не могут умереть;
- они достигают половой зрелости за месяц;
- самки беременны ровно месяц;
- кролики всегда рождаются парами: самка + самец.
Теперь задачу вполне можно решить: ответом на неё как раз будет последовательность Фибоначчи. Логика такая: каждая взрослая пара кроликов будет создавать ещё одну пару через месяц после рождения. Эти кролики-дети будут расти месяц, а потом размножаться с другими кроликами. И так двенадцать месяцев.
Чуть лучше этот процесс можно представить с помощью этой схемы:
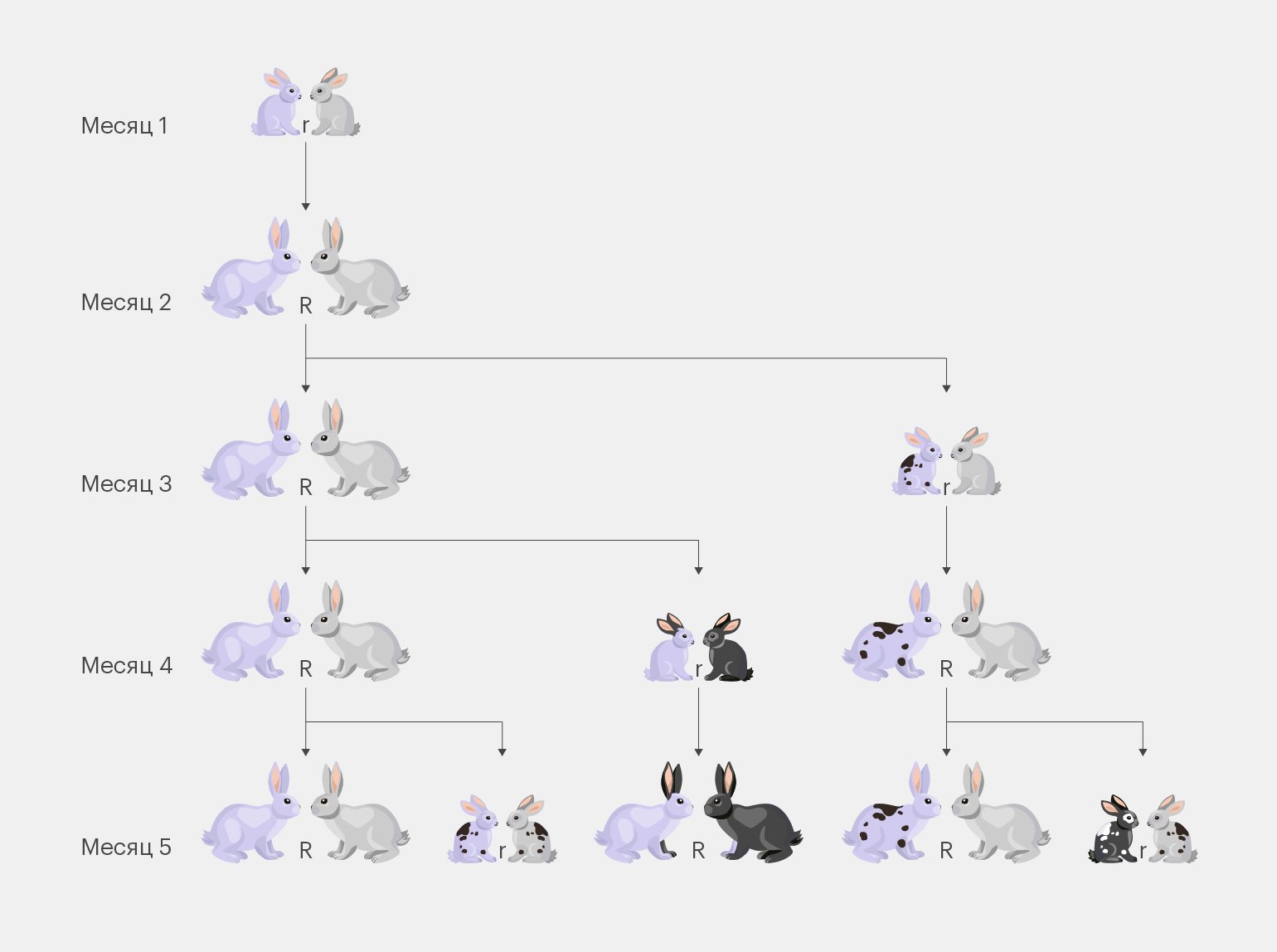
Смотрите, первая пара кроликов ещё совсем молодая, поэтому пока не может дать потомство. Но уже через месяц кролики подрастут и смогут размножаться — соответственно, на третий месяц пар будет уже две. Дальше количество пар будет равняться сумме пар за два предыдущих месяца, и последовательность примет уже знакомый нам вид:

Получаем ответ на задачу: 233 пары кроликов.
И в этом весь смысл чисел Фибоначчи — считать кроликов в загоне? Нет! Оказывается, Леонардо лишь приоткрыл дверь в возможности этой последовательности. Основное применение она нашла в математике, архитектуре и искусстве.
Как связаны числа Фибоначчи и золотое сечение
Архитекторы античных и средневековых городов много времени уделяли идеальным пропорциям. Они хотели создавать красивые постройки, которыми бы наслаждались все жители города. Так появилось понятие золотого сечения.
Золотое сечение — это число, которое помогает делить вещи на красивые части. Оно равно примерно 1,618. Золотое сечение можно найти так: если взять два отрезка чего-то, то большой отрезок должен быть в 1,618 раза больше маленького отрезка, а вся вещь должна быть в 1,618 раза больше большого отрезка. Это число называется «фи» и пишется так: φ.
Читайте также:
Если коротко, когда мы слышим о золотом сечении — речь идёт о чём-то привлекательном и пропорциональном. Например, с помощью золотого сечения спроектированы знаменитые архитектурные сооружения прошлого:

Изображение: Dimitris Koskinas / Shutterstock / Skillbox Media

Изображение: Anton Belo / Shutterstock / Skillbox Media
Вернёмся к числам Фибоначчи. Оказывается, отношение каждого числа к предыдущему примерно равно значению золотого сечения. Правда, на первых числах последовательности этого не будет заметно:
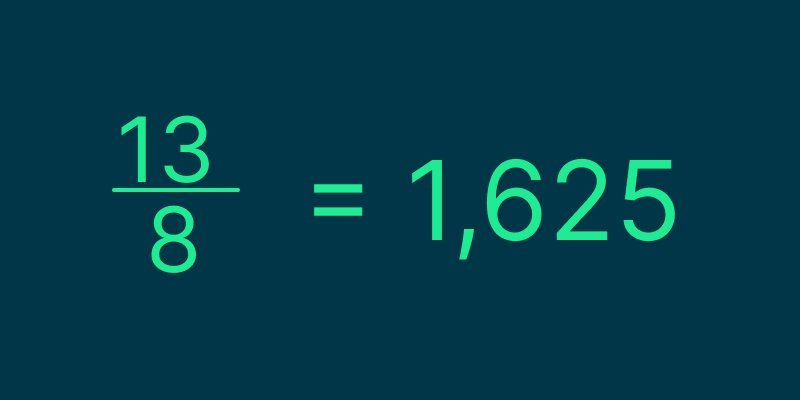
Но если мы возьмём, например, тридцать первое число и поделим на тридцатое, то получим следующее:
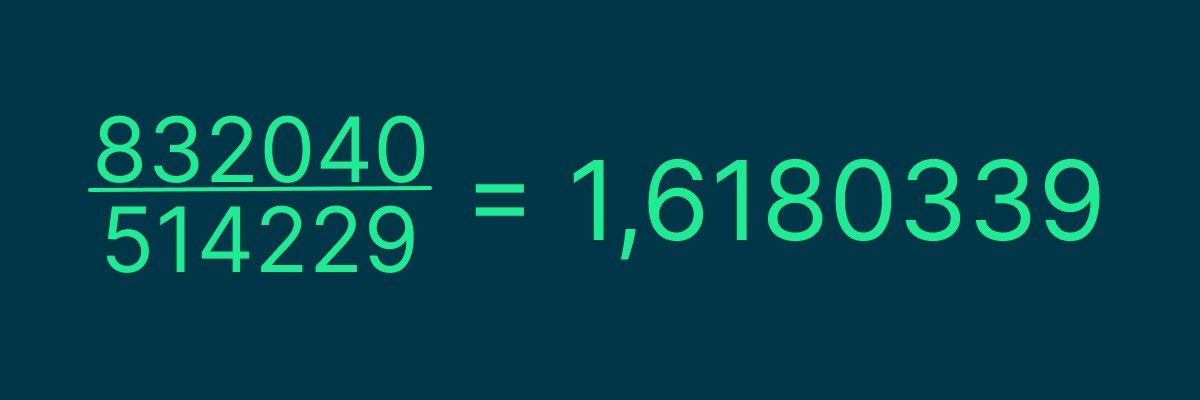
И ещё пара тысяч знаков после запятой. Оно очень похоже на значение золотого сечения, но всё же не равно ему точно. А чем дальше мы идём по числам, тем ближе к нему будет приближаться это отношение.
Золотое сечение используется не только в архитектуре, но и, например, в фотографии, живописи и дизайне. Даже некоторые интерфейсы сайтов сделаны по этим принципам:

Изображение: tubik / Dribbble
Но и на этом применение последовательности Фибоначчи не заканчивается. Дальше мы узнаем, как эти числа использует сама природа и какое применение они нашли в программировании.
Где используются числа Фибоначчи
Числа Фибоначчи нашли своё применение не только в математике, но и в других науках и даже в творчестве. Они описывают природные явления и помогают людям больше зарабатывать на акциях. Давайте посмотрим поближе на всё это.
Числа Фибоначчи в природе
Первое, на чём можно проследить последовательность Фибоначчи, — это растения, а конкретно — подсолнух. Скорее всего, вы видели его в детстве и, возможно, даже пробовали жарить семечки на сковородке.
Оказывается, семена внутри цветка расположены в виде двух рядов спиралей — коротких и длинных. Первые наклонены по часовой стрелке, а вторые — против. Смысл в том, что количество коротких спиралей в подсолнухе равно 21, а длинных — 34. А это как раз соседние числа в последовательности Фибоначчи.

Фото: NataBystrova / Shutterstock
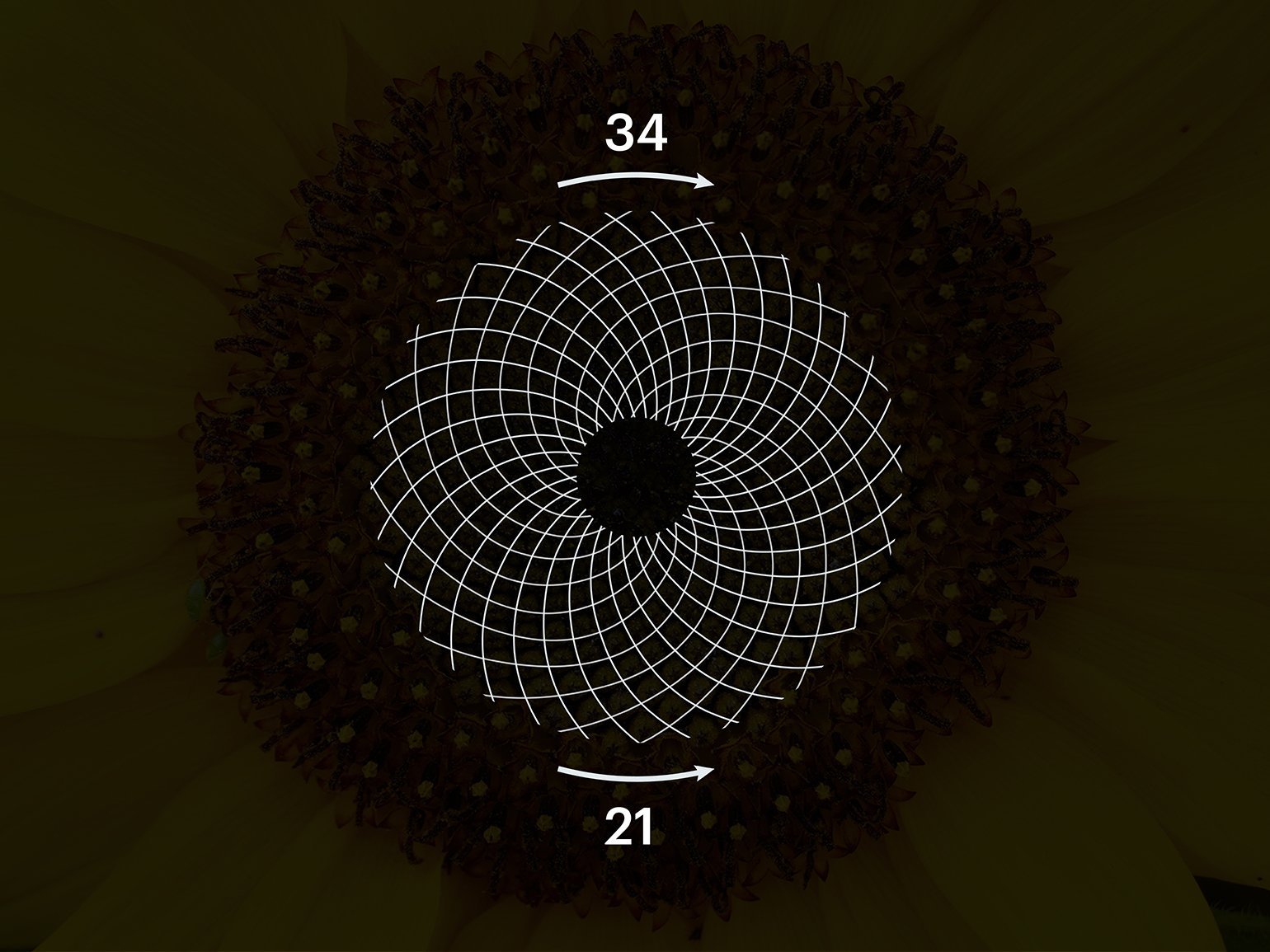
Ещё числа Фибоначчи можно встретить, если посмотреть на стебли и ветви деревьев. Каждая ветвь создаёт новые ветви, количество которых равно следующему числу в последовательности Фибоначчи.
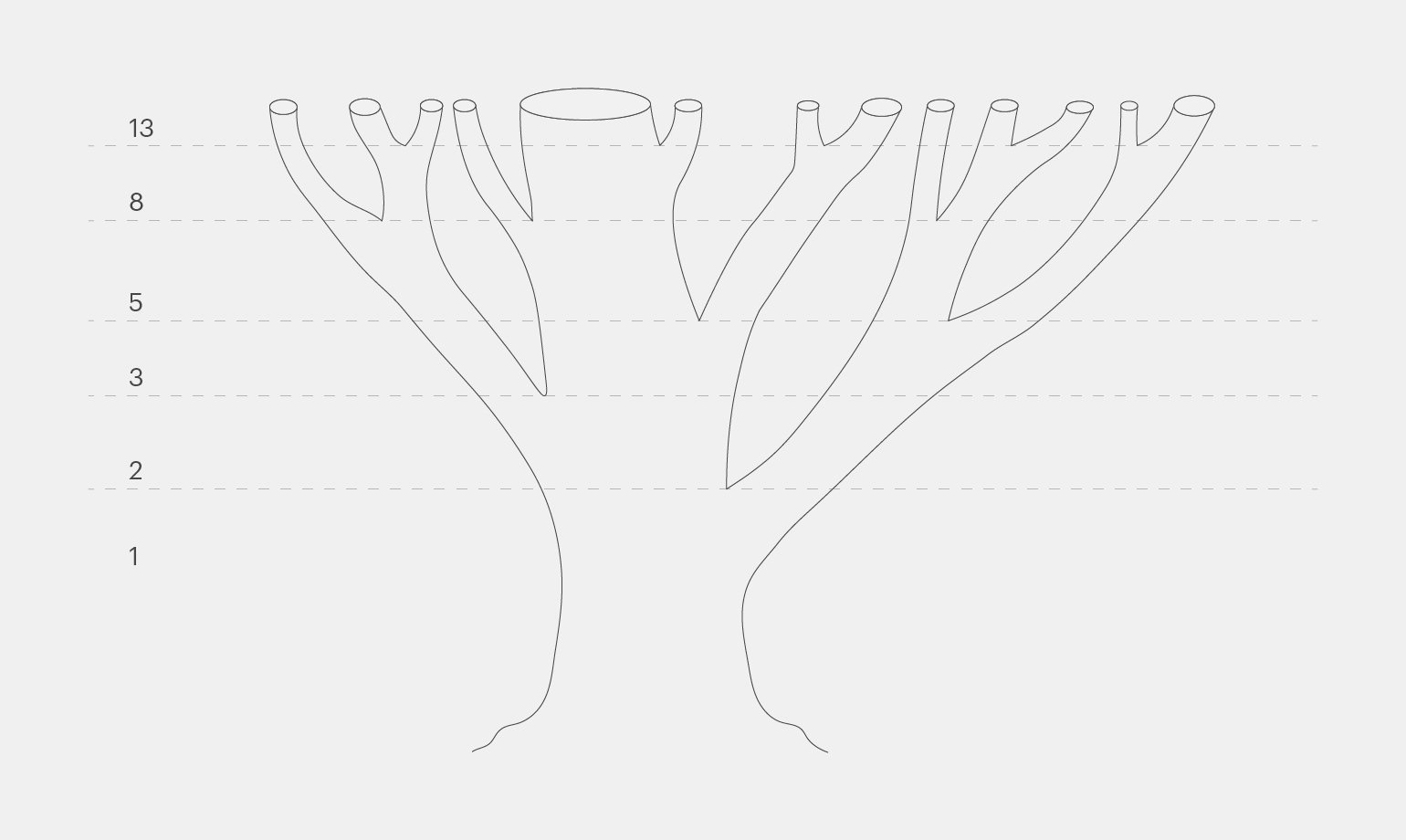
Инфографика: Майя Мальгина для Skillbox Media
Если говорить о золотом сечении, то по нему закручиваются панцири улиток, вихри ураганов и даже некоторые галактики. Если ещё не убеждены, что мы живём в матрице, то вот доказательства:
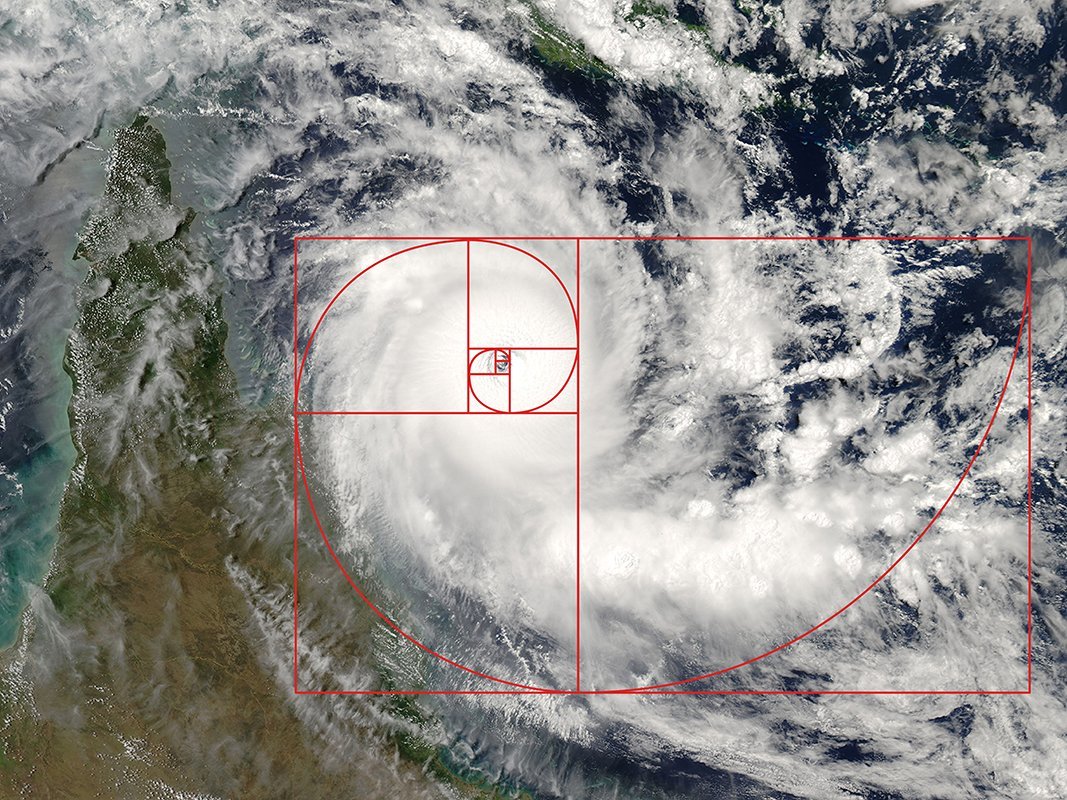
Изображение: NASA / Skillbox Media

Изображение: NASA / Skillbox Media
Как видите, природа прямо-таки пронизана магией чисел Фибоначчи, причём на всех уровнях: от семян подсолнуха до далёких галактик. Поэтому не стоит удивляться, если вдруг встретите эту последовательность где-нибудь в привычном для вас месте.
Числа Фибоначчи в искусстве и дизайне
Мы уже рассказали, как некоторые архитекторы древности и античности использовали числа Фибоначчи для создания известных построек. Давайте теперь поговорим и о других сферах искусства.
Часто художники используют золотое сечение, чтобы эстетично располагать объекты на картине и создавать гармоничные образы. Фотографы пользуются такими же хитростями:

Изображение: lehic / Shutterstock / Skillbox Media
Ещё числа Фибоначчи помогают создавать более пропорциональные лица, фигуры людей и другие элементы. Так картины приобретают реалистичный вид:
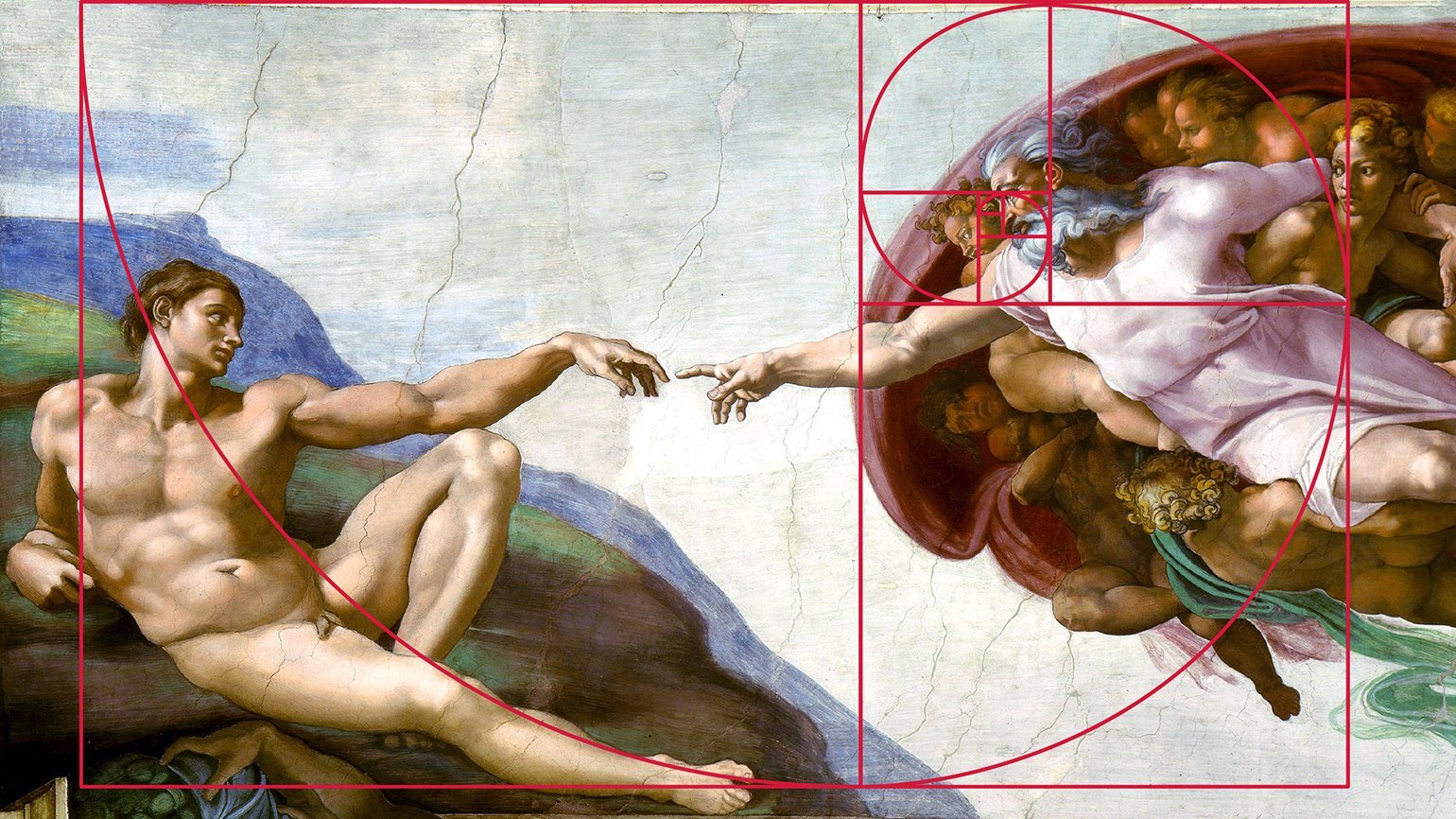
Изображение: Микеланджело Буонарроти, «Сотворение Адама», около 1511 г. / Vatican Museums
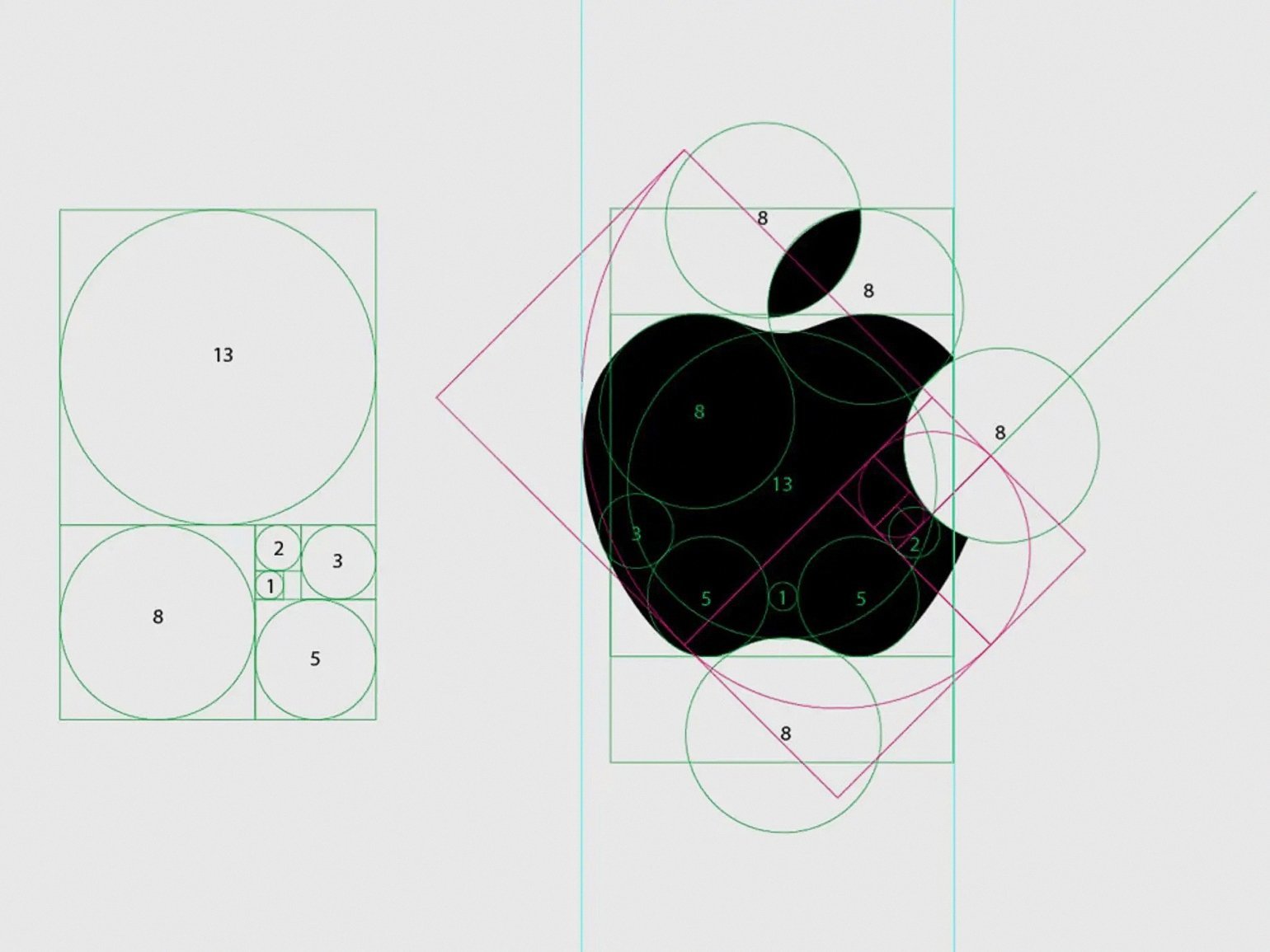
Дизайнеры тоже подхватили эту идею и начали использовать золотое сечение в своих макетах. Например, по этим правилам можно создавать более приятные глазу логотипы. В той же Apple, к слову, давно поняли, что золотое сечение — это круто. В её фирменном знаке как раз используются повторяющиеся спирали, навеянные числами Фибоначчи.
Древние греки одними из первых углубились в эту тему. Для них золотое сечение было символом красоты и гармонии. На этих принципах они даже разработали понятие канонических пропорций, которые легли в основу, например, известных античных скульптур богов, героев и атлетов.
Самый яркий пример — статуя Давида работы Микеланджело.

Изображение: Jörg Bittner Unna / Wikimedia Commons / Skillbox Media
Однако золотое сечение — это вовсе не панацея и универсальный канон красоты. Хотя некоторые исследования показывают, что существует сходство между золотым сечением и аспектами человеческого тела, такими как пропорции лица и тела. Но прямых доказательств нет, потому что красота — неизмерима.
Числа Фибоначчи в финансах и программировании
А теперь давайте разберёмся, как последовательность Фибоначчи себя чувствует в естественной среде обитания — то есть в сферах, связанных с логикой и вычислениями.
Финансы и биржевая торговля. Трейдеры используют числа Фибоначчи для анализа изменений на рынке. Они помогают определить, когда цена акции может вырасти или упасть.
Кадр: Warrior Trading / YouTube
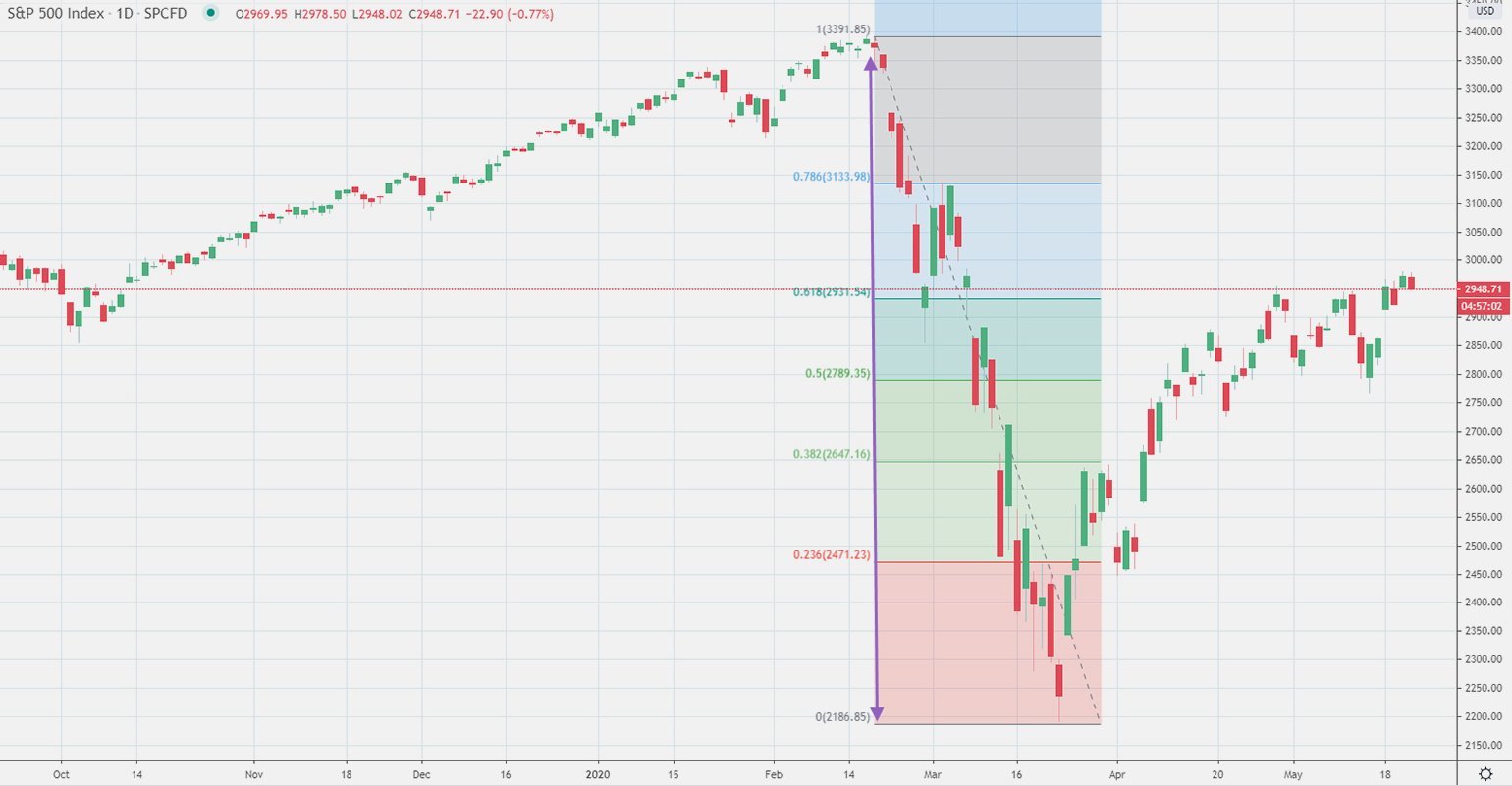
Трейдеры применяют эту последовательность в виде так называемых Фибоначчи-уровней, которые строятся на графике, чтобы определить потенциальные возможности для роста и падения стоимости акции.
Уровни Фибоначчи помогают трейдерам определить места, где цена может расти или падать. Чаще всего это происходит на трёх уровнях — 38,2%, 50% и 61,8%. Однако это работает не всегда точно, потому что на цену могут повлиять случайные факторы — например, внезапная пандемия.
Программирование. Здесь последовательность Фибоначчи используют для создания криптографических алгоритмов и 3D-моделей. А ещё, конечно же, лекторы часто добавляют в свои курсы задачки на нахождение этих чисел ?
Вот как алгоритм выглядит на языке Python. Функция принимает на вход номер числа в последовательности, а выдаёт — само число Фибоначчи.
def fib(n):
if n in (1, 2):
return 1
return fib(n - 1) + fib(n - 2)
print (fib(10)) # Выведет 55Работает функция так:
- Получает на вход номер числа в последовательности Фибоначчи, которое мы хотим найти.
- Далее смотрит на базовые случаи — первое или второе число последовательности. Тогда функция сразу возвращает единицу.
- Если номер числа Фибоначчи больше двух, алгоритм возвращает сумму двух предыдущих чисел последовательности — или значение этой же функции, но с меньшими аргументами. Это называется рекурсией.
- Функция будет вызывать сама себя, пока не встретится базовый случай. Тогда она передаст значение по цепочке вверх и рекурсия закончится.
Рекурсия может показаться запутанной. Поэтому мы сделали отдельную статью, где рассказываем основные принципы на жизненных примерах.
Специалисты по криптографии используют числа Фибоначчи, чтобы генерировать псевдослучайные числа. Приставка «псевдо» используется потому, что эти числа не являются по-настоящему случайными и с какого-то момента начинают повторяться.
Генераторы псевдослучайных чисел применяют для создания ключей шифрования, криптографических хеш-функций и протоколов. Смысл в том, что последовательность Фибоначчи обладает свойством непредсказуемости и значения функций не повторяются до определённого момента.
Вместо заключения
Когда мы готовили этот материал, наш редактор вспомнил диалог из старой детской книжки «В лабиринте чисел» — кажется, он идеально подходит для финала статьи о числах Фибоначчи.
Приводим его полностью:
Чит недоумённо пожал плечами. Ряд как ряд! Что в нём интересного?
— Не скажи, — живо возразила Ари. — У чисел Фибоначчи куча удивительных свойств. Взять, например, дерево — из тех, что ветвятся ежегодно. Если на втором году жизни у него два ответвления, то на третьем их уже будет три, на четвёртом — пять, на пятом — восемь, на шестом — тринадцать и так далее. А ведь всё это числа Фибоначчи! С тем же рядом связано и расположение листьев на ветке, и количество завитков, образованных семечками подсолнуха, чешуйками сосновой шишки или ананаса… Как видишь, природа широко пользуется числами Фибоначчи.
— A люди? — неожиданно выпалил Чит. — Они-то ими пользуются?
— Где людям угнаться за природой! Долгое время о числах Фибоначчи просто не знали. Но и потом они оставались безработными много столетий. И только в нынешнем, двадцатом веке им нашлось наконец дело. Во-первых, подобно булевой алгебре и теории множеств, числа Фибоначчи используются в вычислительных и думающих машинах. Во-вторых, с их помощью были решены некоторые математические задачи. Ну да о них ты узнаешь в своё время. Как ещё сработает этот удивительный числовой ряд, сказать трудно. Ясно одно: бесполезных открытий не бывает.







