Простыми словами: что такое бином Ньютона
Бином Ньютона — это совсем не rocket science. Смотрим в глаза страху и раскладываем по полочкам знаменитую формулу.


Про бином Ньютона часто говорят, что это настолько сложная штука, что по сравнению с ней всё остальное меркнет. Но на самом деле магия бинома — как раз в простоте и скорости. Например, он сильно упрощает вычисления при разработке нейросетей, сетевых протоколов и алгоритмов шифрования.
Поэтому, если видите себя в будущем в data science или криптографии, разобраться с биномом Ньютона будет полезно. А если даже и нет — сможете уверенно отвечать друзьям в духе: «Видал я этот ваш бином, там всё проще пареной репы». Тоже какой-никакой, но профит. А теперь к делу.
Что такое бином Ньютона
Бином Ньютона — это формула, которая помогает возвести сумму двух чисел в любую степень. Особенно она полезна, если степень большая.
Из уроков математики мы помним такую формулу: (a + b)2 = a2 + 2ab + b2. Это тоже бином Ньютона, а точнее — его частный случай для разложения на множители квадрата суммы.
Выглядит вроде бы просто. Но представьте, сколько нужно совершить операций умножения, чтобы возвести эту же сумму, например, в седьмую степень. В конечной формуле будет аж восемь слагаемых:
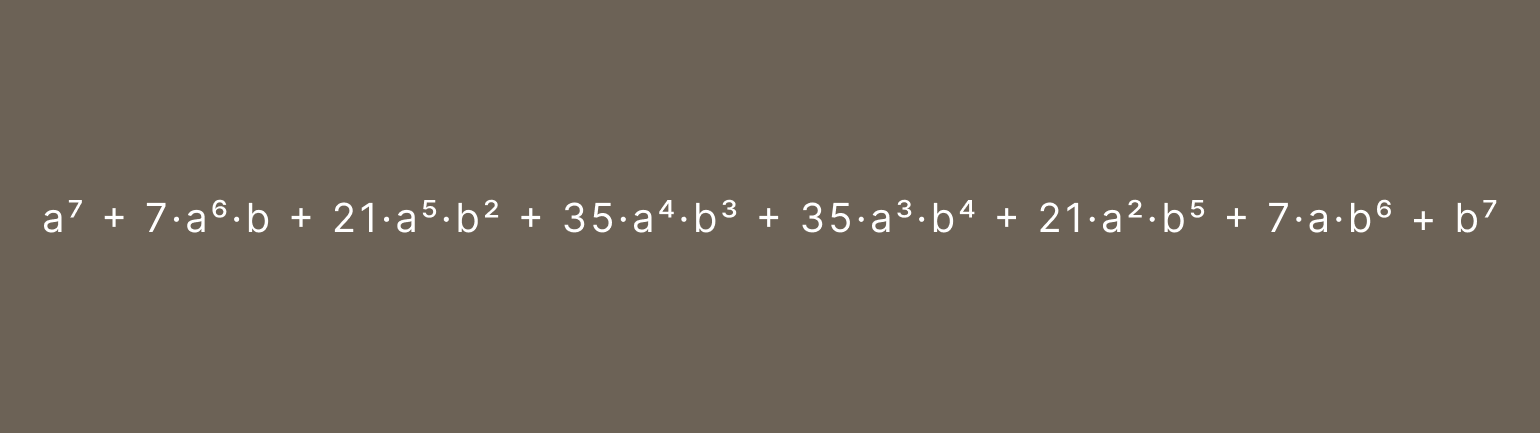
Чтобы упростить этот процесс и не тратить столько времени на простые арифметические операции, как раз и придумали бином Ньютона.
Разбираем формулу бинома Ньютона
Сорвём пластырь сразу — вот как выглядит та самая формула бинома Ньютона:
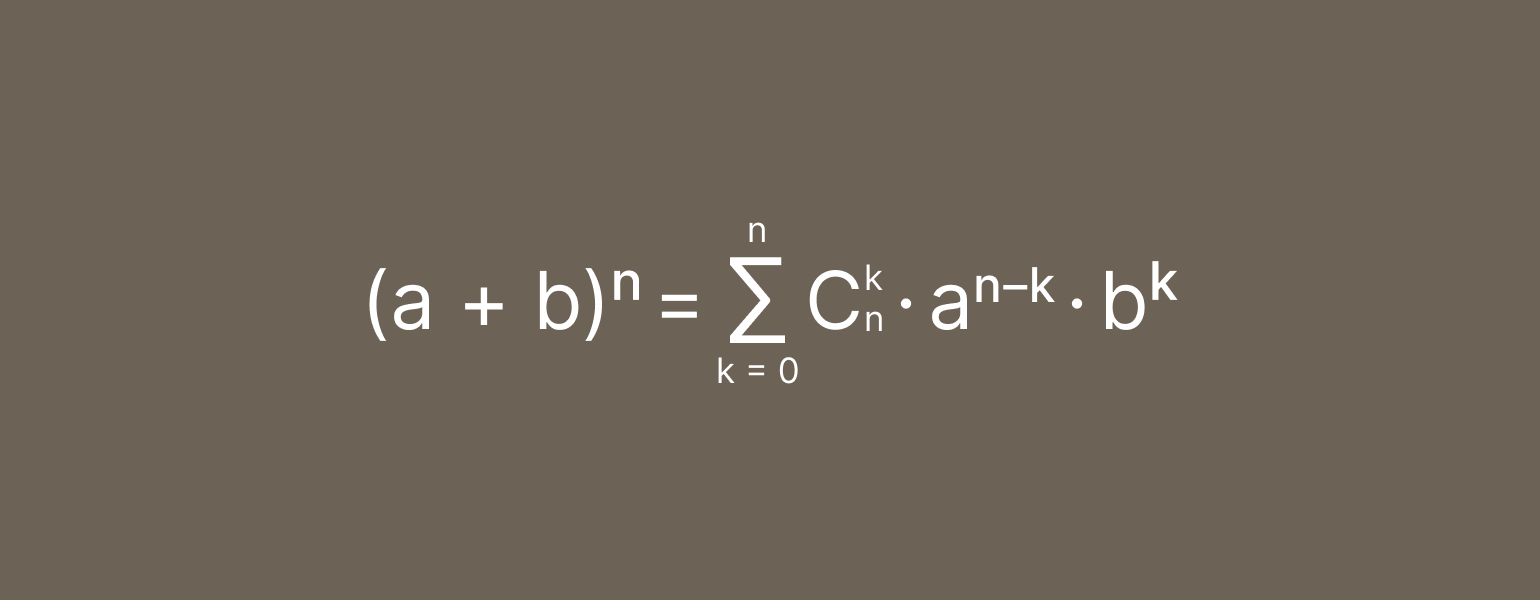
Сразу возникает миллион вопросов: что это за странная большая буква Е? Что такое C? И что вообще здесь происходит? Сейчас во всём разберёмся.
a и b — это два числа, которые мы складываем, а затем хотим возвести в степень n. Числа в скобках могут быть любыми — хоть положительными, хоть дробными, хоть отрицательными. А вот степень обязательно должна быть натуральным числом, то есть целым, положительным, не равным нулю.
Большая буква, похожая на Е, — это на самом деле «сигма», знак алгебраической суммы. Её используют, чтобы сократить длинные операции сложения. Например, такие:
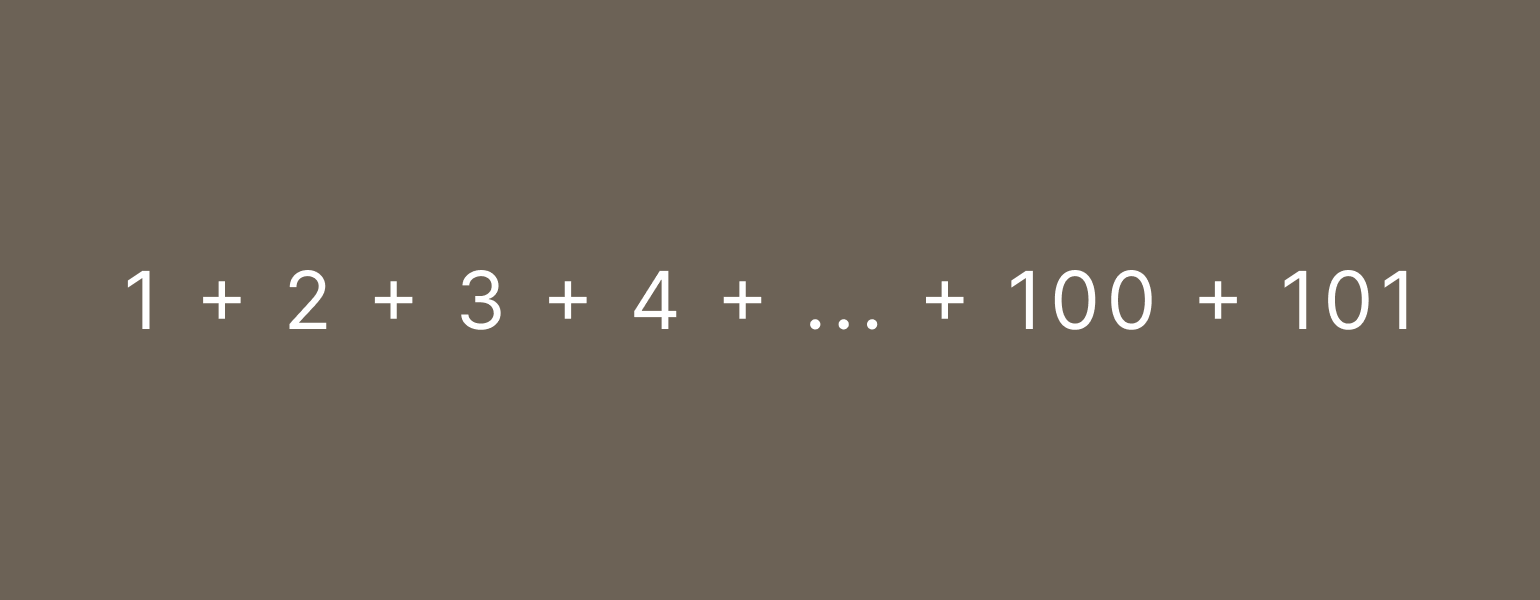
То же самое выражение, записанное с помощью сигмы:

Здесь мы добавляем букву n, которая представляет собой все числа от 1 до 101 по порядку. Под знаком суммы мы указываем, с какого числа начинаем считать, а сверху — на каком заканчиваем. Получается, это выражение просуммирует все числа от 1 до 101 (ответ: 5151).
А вот как выглядит формула бинома Ньютона без знака суммы:
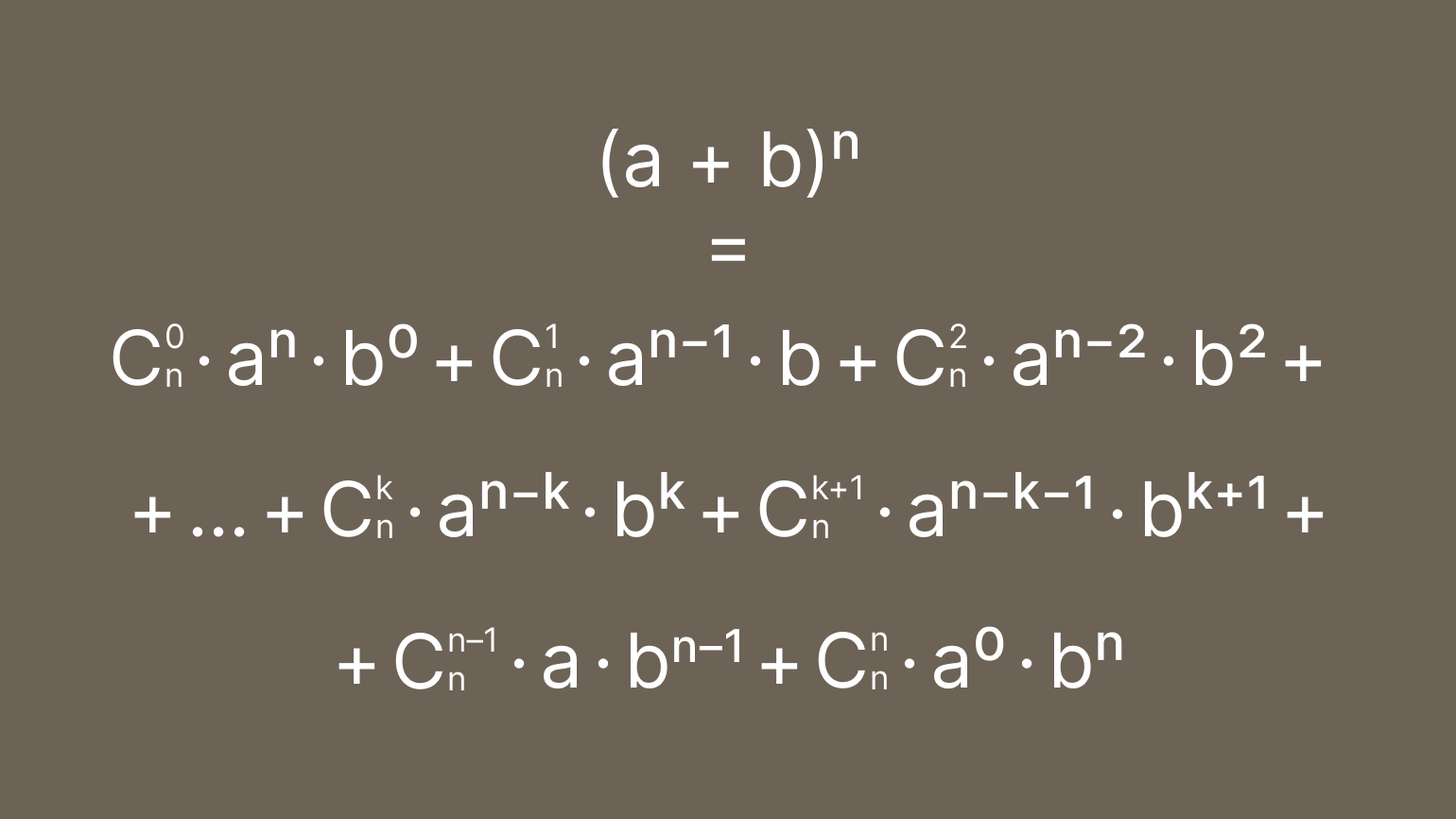
Получили очень много цифр и букв, в которых легко потеряться. Но не забывайте, что это общая формула, а значит, она может быть запутанной.
Теперь переходим к более сложным вещам — биномиальным коэффициентам, которые обозначаются буквой C. Они показывают, на какие числа нужно умножить каждое слагаемое в многочлене. Например, в выражении a2 + 2ab + b2 слагаемыми будут a2, ab и b2, а их коэффициентами: 1, 2 и 1.
Посчитать биномиальные коэффициенты можно с помощью этой формулы:
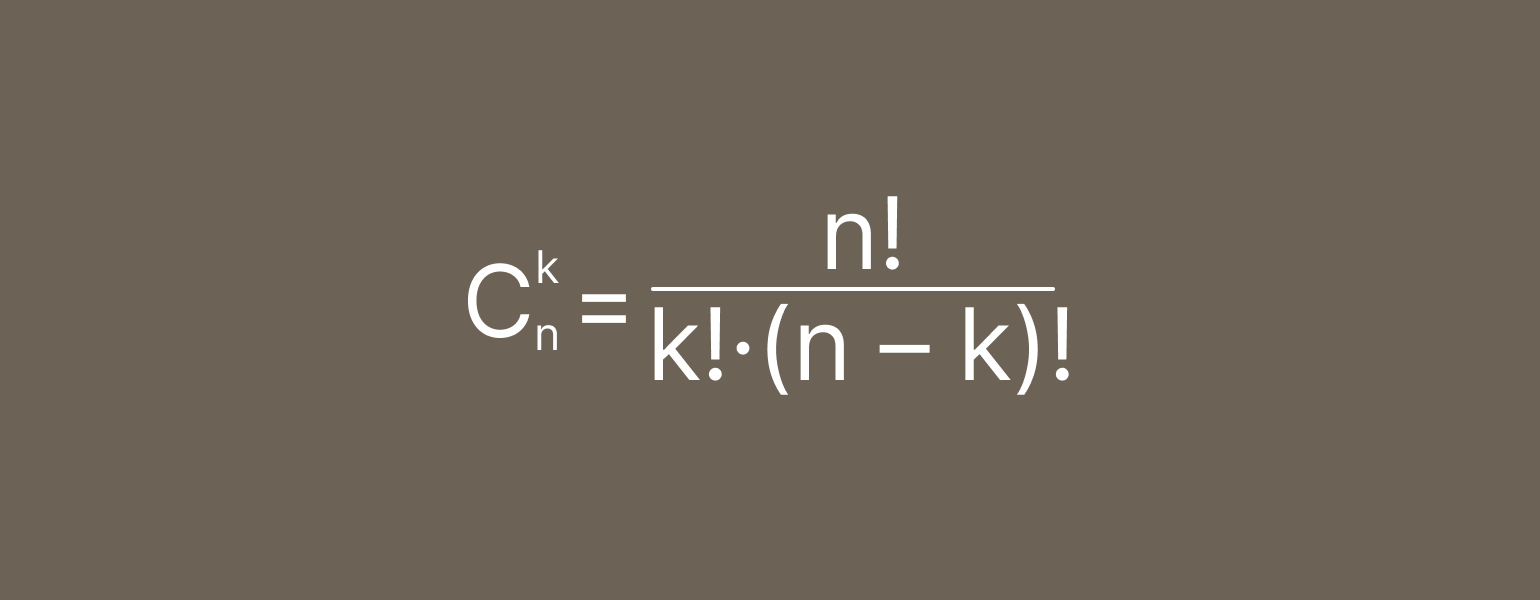
Здесь n — это степень, в которую мы возводим сумму двух чисел. k — номер слагаемого в многочлене (считается с нуля). Восклицательный знак — это символ факториала. Факториал — это произведение всех чисел от 1 до числа, стоящего под знаком факториала. Например, 4! = 1 × 2 × 3 × 4 = 24.
Читайте также:
А покажите, как считать
С определениями закончили, теперь давайте попрактикуемся. Если сейчас что-то непонятно, сначала посмотрите примеры, а затем снова возвращайтесь к формуле.
Попробуем применить формулу бинома Ньютона к сумме a + b, возведённой в квадрат. Подставляем значения:
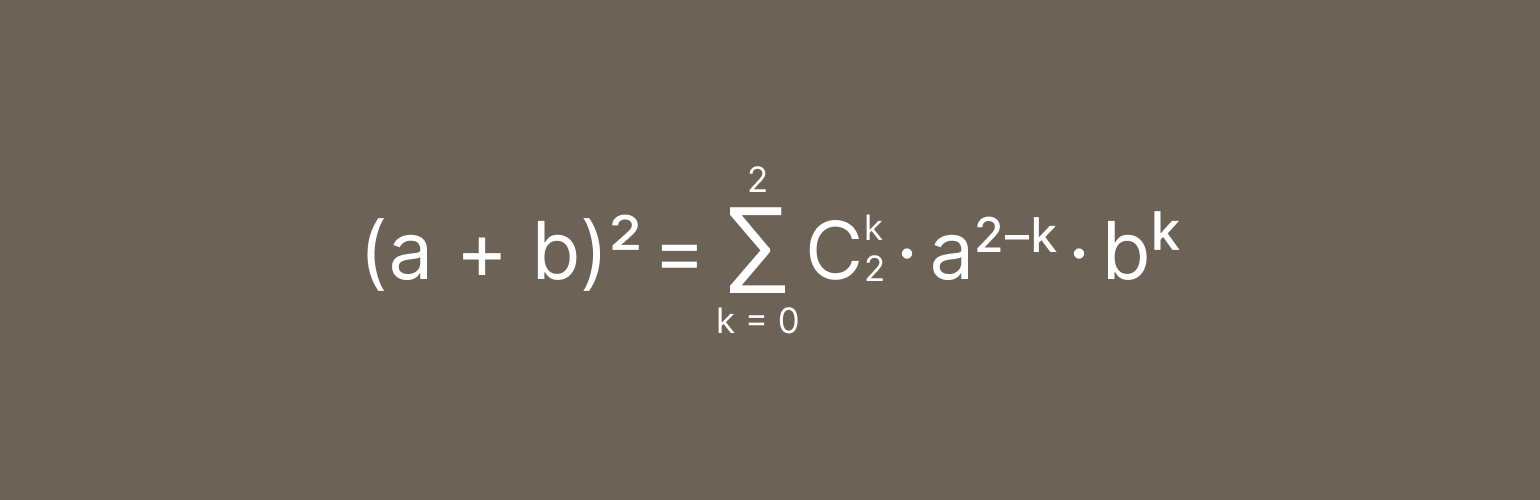
Теперь раскроем знак суммы и выпишем все слагаемые, но пока не будем считать биномиальные коэффициенты:
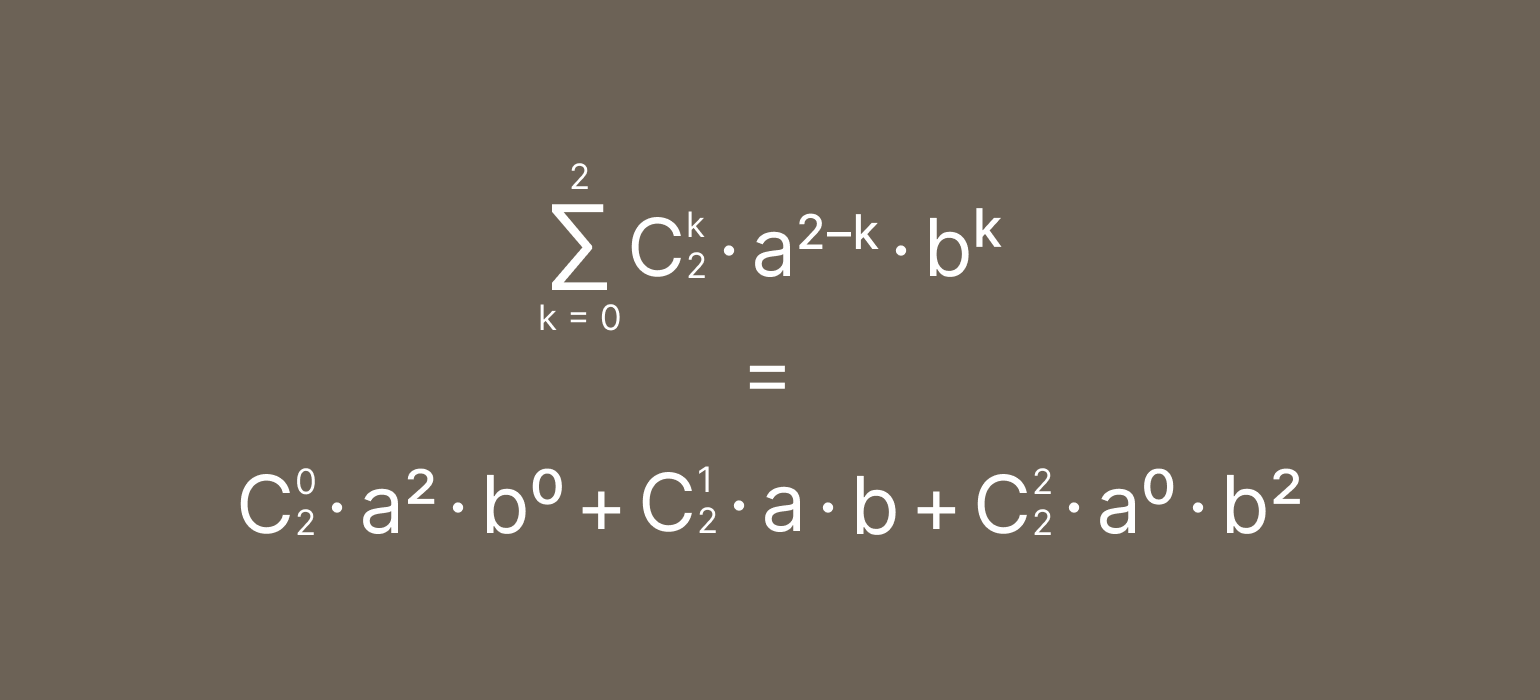
Теперь давайте немного упростим выражение. По свойствам степеней, если число возводится в нулевую степень, то оно равно единице. Поэтому b0 и a0 мы можем заменить на единицы:
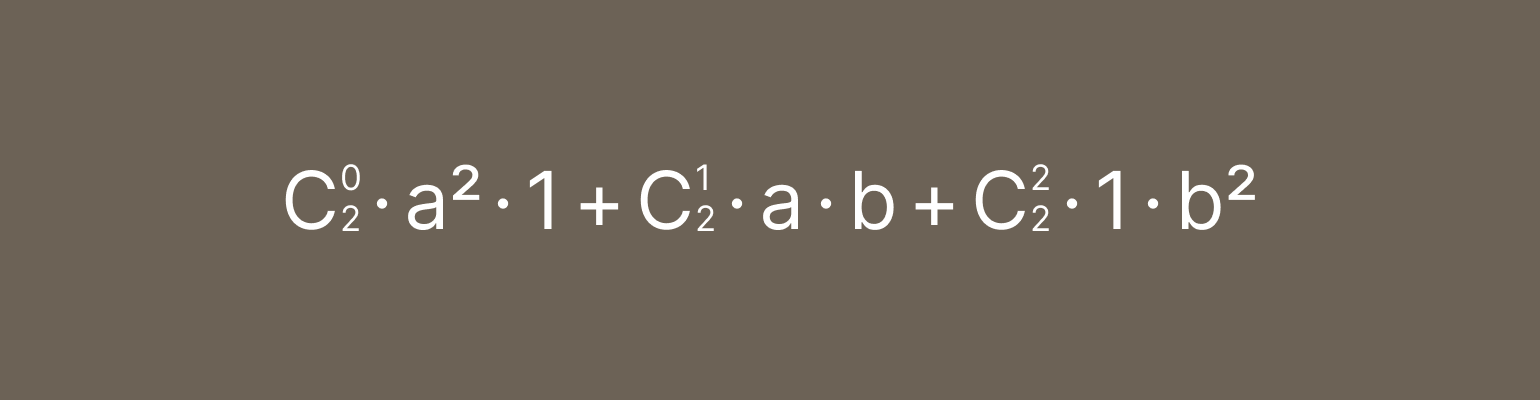
Со степенями разобрались — теперь считаем биномиальные коэффициенты с помощью формулы:
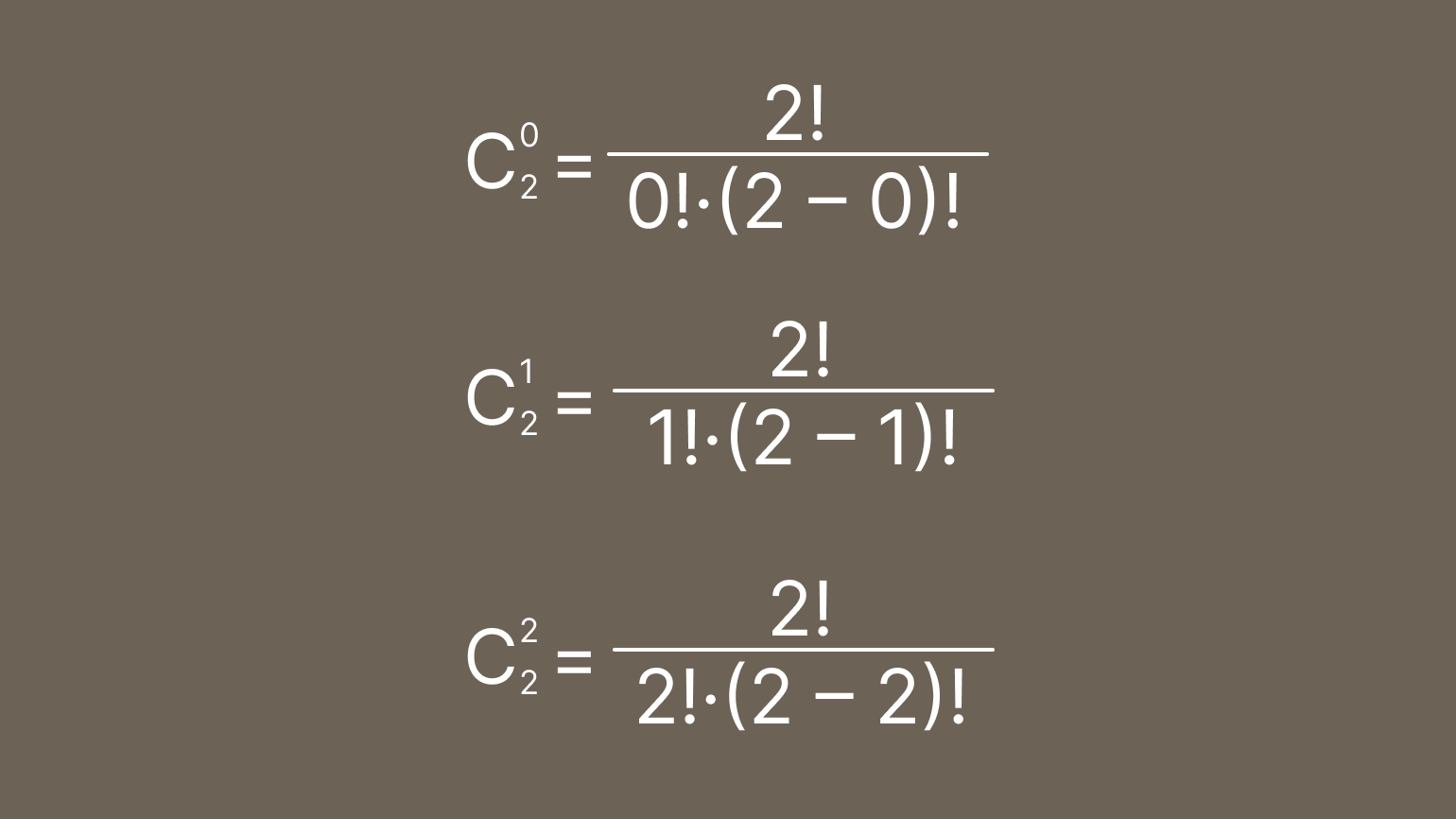
Осталось посчитать значения факториалов и сократить дроби. Помним, что факториал нуля равен единице, а одинаковые факториалы можно сокращать:
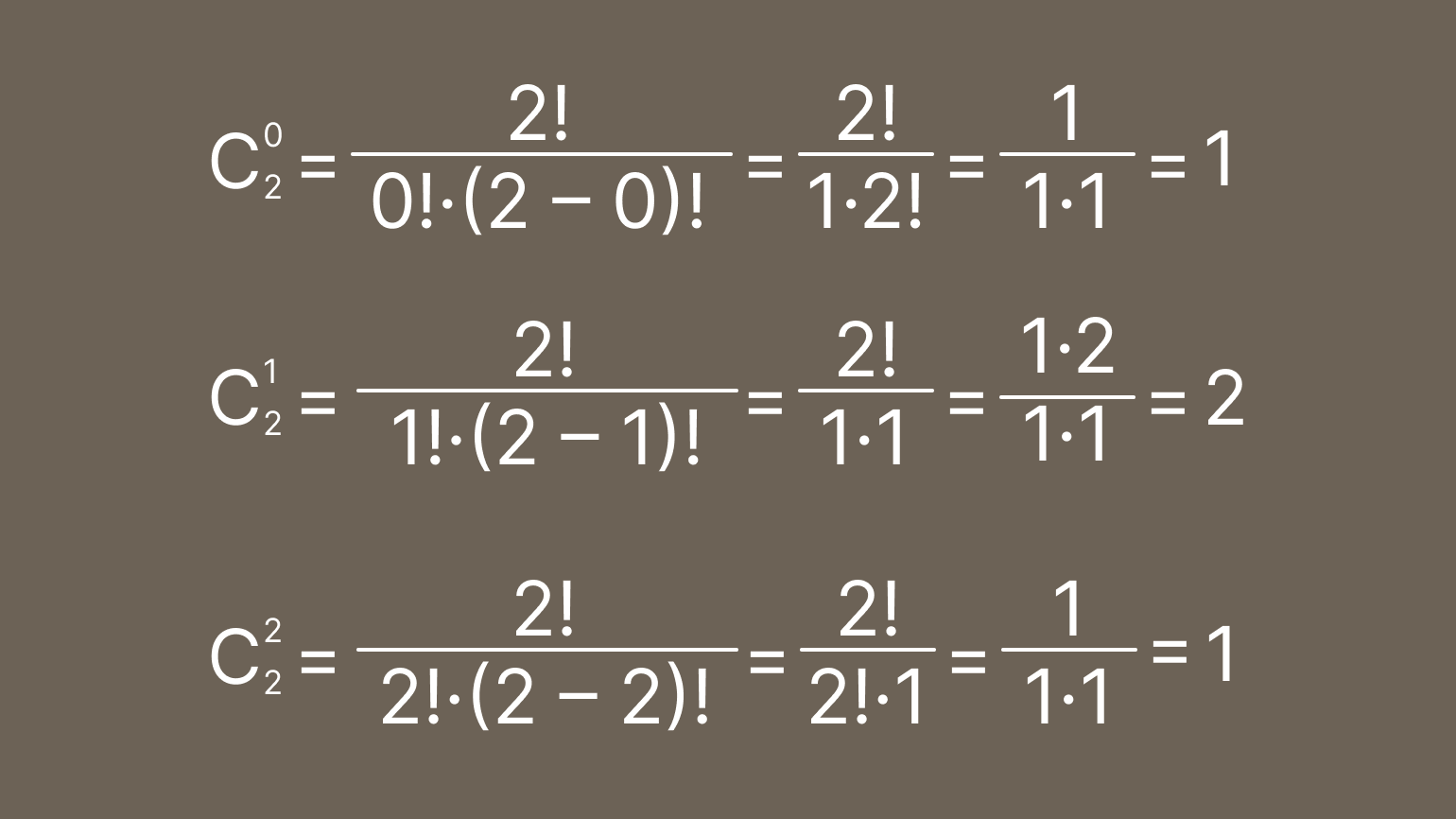
Подставляем коэффициенты в нашу формулу:
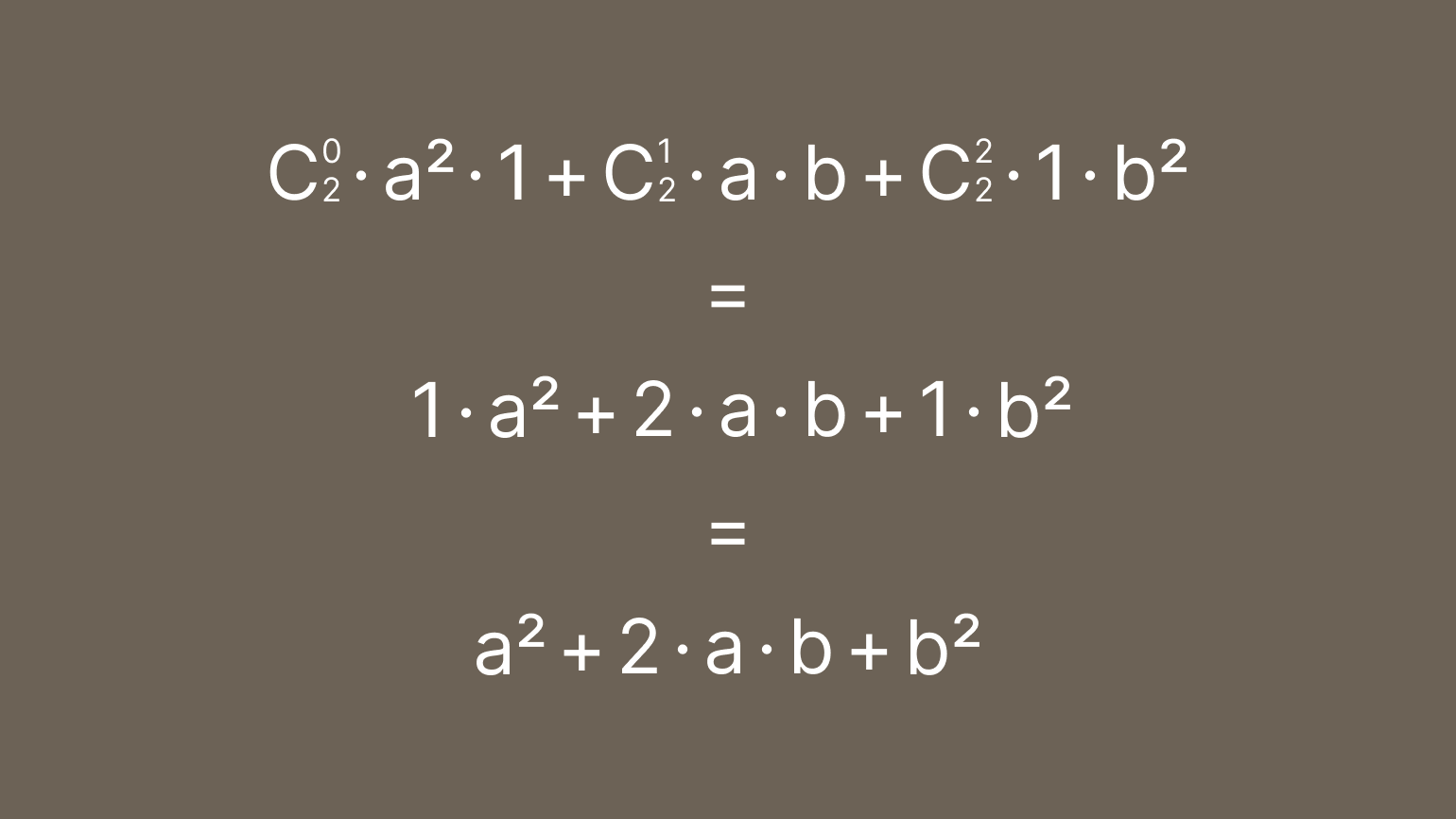
Получаем наше выражение для квадрата суммы. Всё правильно.
Таким же способом можно находить слагаемые для степеней и побольше. Давайте для примера посчитаем по формуле бинома Ньютона сумму двух чисел, возведённую в четвёртую степень:
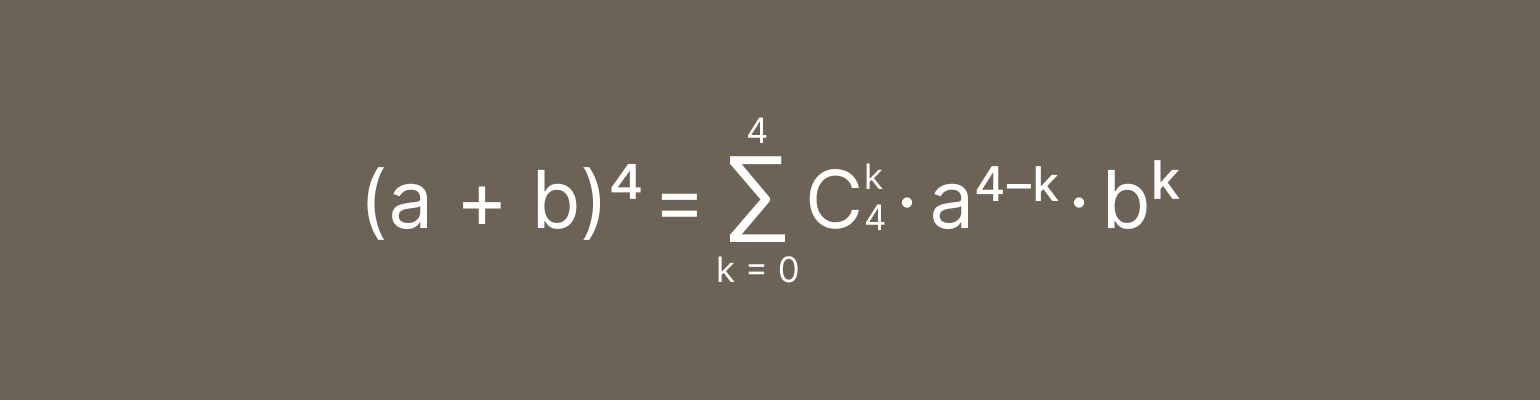
Вычислим сразу коэффициенты:
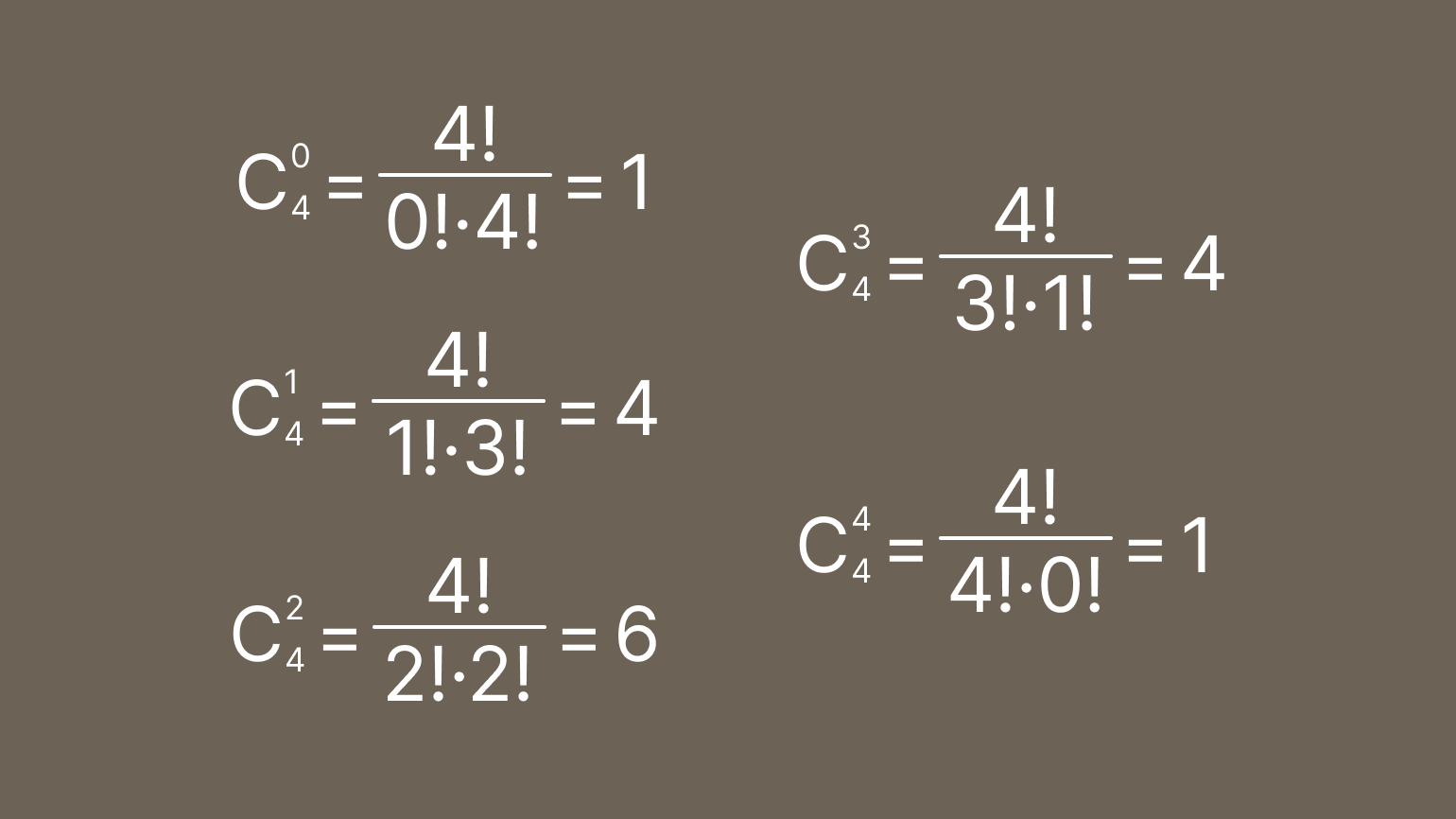
? Обратите внимание
Значения биномиальных коэффициентов повторяются. Первый равен последнему, а второй — четвёртому. Поэтому можно считать не все коэффициенты, а только половину (ну и ещё один «посередине», если степень многочлена чётная).
Сразу подставляем коэффициенты в сумму и считаем степени слагаемых:
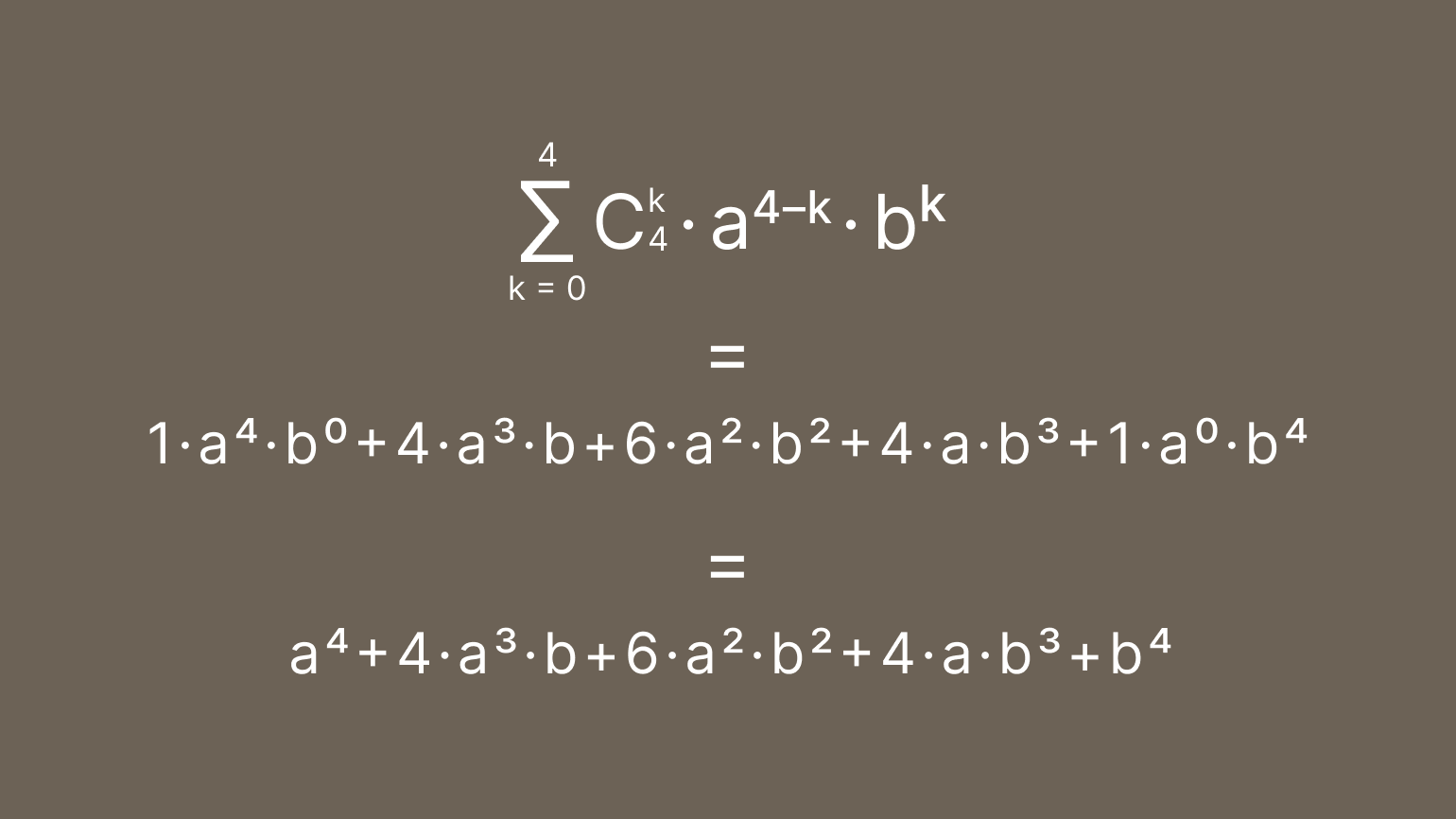
Получаем нужное нам выражение. Можете проверить это выражение, перемножив все множители друг с другом. Если, конечно, вам хватит терпения ?
Как проще вычислять коэффициенты с помощью треугольника Паскаля
Треугольник Паскаля — это специальный треугольник чисел, который помогает считать биномиальные коэффициенты. Каждое число в нём равно сумме двух чисел, расположенных над ним. На вершине и по рёбрам треугольника расположены единицы.
Первые пять строк треугольника Паскаля выглядят так:
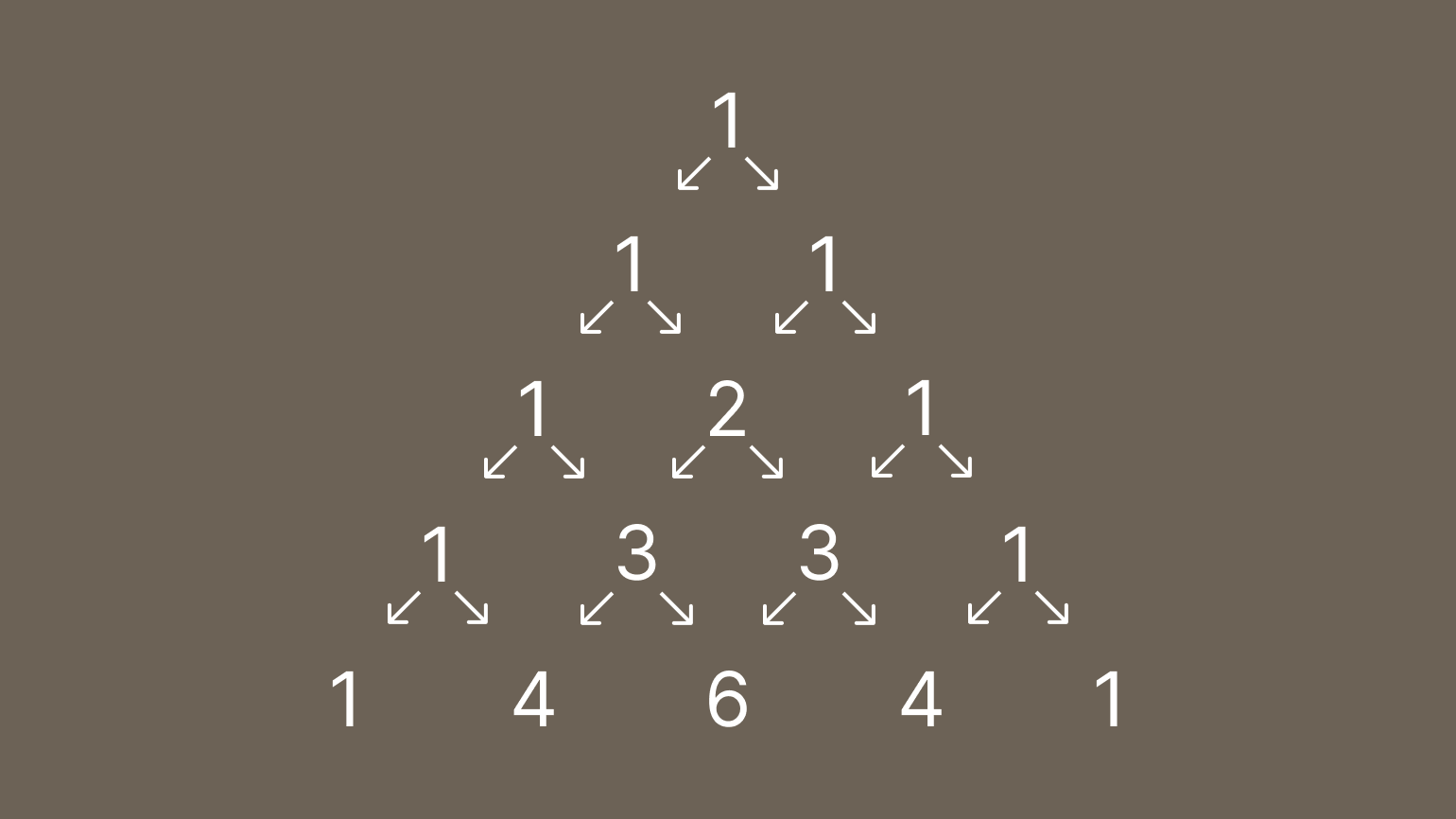
Фишка этого треугольника в том, что нам не нужно много раз считать факториалы, чтобы найти биномиальные коэффициенты. Всё, что необходимо, — это сложить несколько чисел.
Давайте для примера вычислим коэффициенты для суммы чисел, возведённой в пятую степень:
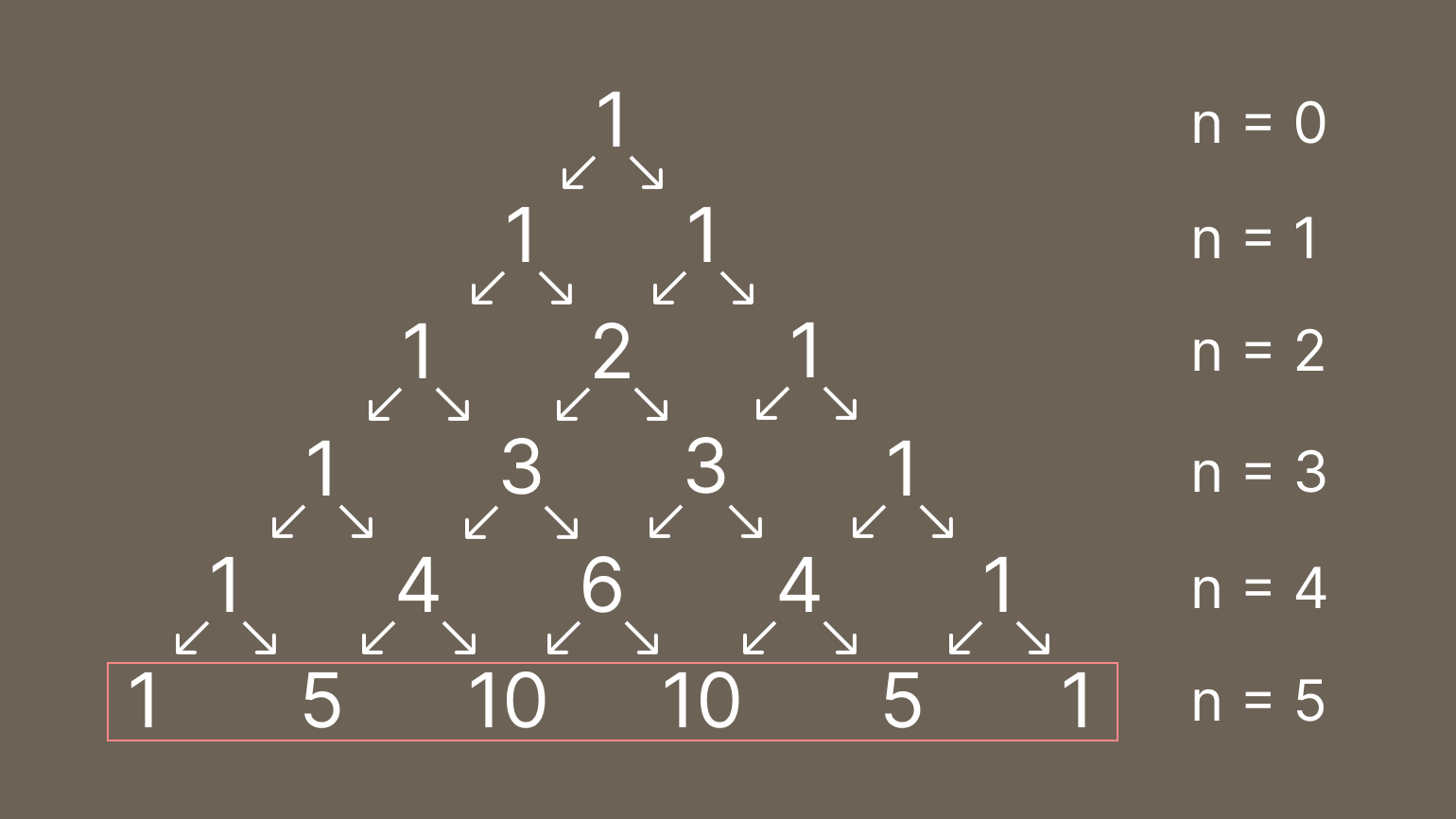
Теперь подставим их в наше выражение — то есть возведём сумму (a + b) в пятую степень. Для этого используем формулу бинома Ньютона:
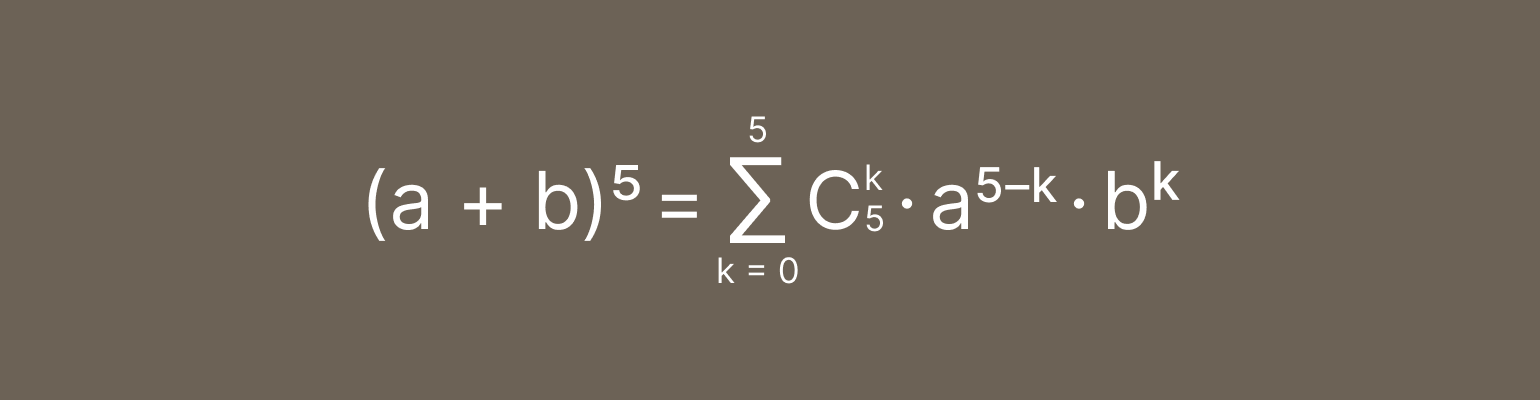
Раскладываем на слагаемые, но пока не считаем коэффициенты:
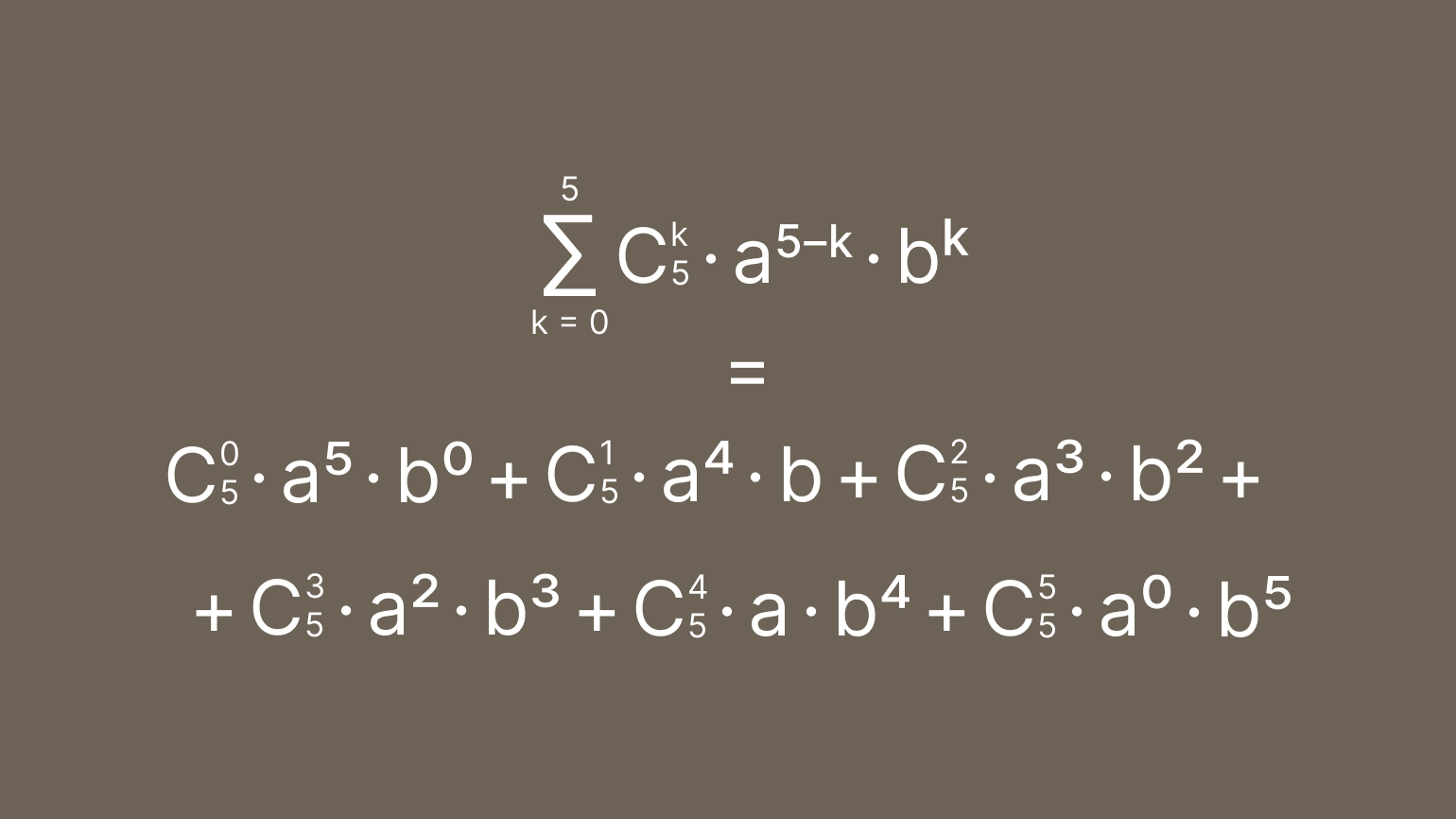
Заменяем по очереди биномиальные коэффициенты на числа из треугольника Паскаля:
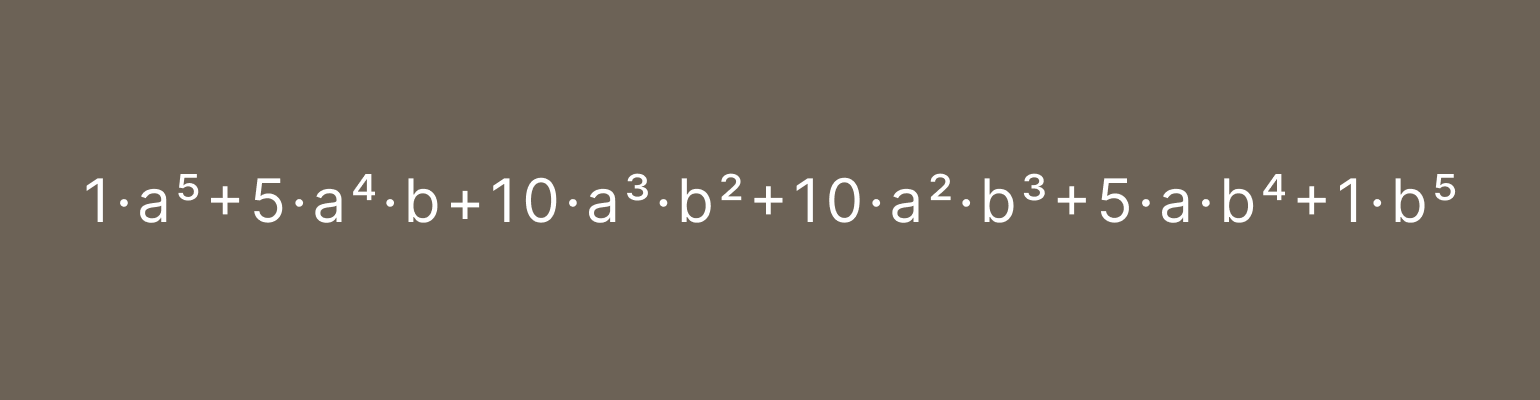
Получаем нужную формулу. Можете проверить и пересчитать коэффициенты классическим способом — с помощью факториалов.
Где используют бином Ньютона
Стоит ли говорить, что чаще всего бином Ньютона используют в математике — вот в каких её разделах он незаменим:
- Теория вероятностей — чтобы вычислять вероятности нескольких независимых событий. Например, вероятности выпадения решки при подбрасывании монеты пять раз подряд.
- Комбинаторика — чтобы вычислять количество возможных комбинаций и перестановок для объектов.
- Статистика — чтобы оценивать вероятность успеха или неудачи в случайных экспериментах. Например, мы можем заранее просчитать, какое количество товаров на фабрике будет бракованным.
Но одной математикой всё не ограничивается — вот несколько сфер науки и техники, где бином Ньютона тоже активно используется:
- Физика и механика — для вычисления вероятностей результатов экспериментов с частицами и для описания поведения частиц при столкновениях.
- Инженерные науки — для оценки вероятности отказа компонентов в системе.
- Программирование — для создания алгоритмов сжатия данных, криптографии и решения задач, связанных с комбинаторикой и вероятностями.
- Биология и генетика — для анализа частоты определённых генотипов или фенотипов в популяциях. А ещё бином Ньютона незаменим при моделировании результатов генетических кроссов и передачи наследственных характеристик.
В общем виде принцип такой: бином Ньютона используют везде, где нужно просчитывать вероятности и комбинации различных предметов и событий.
Что дальше
Будем продолжать разбираться с математическими понятиями, которые используют в комбинаторных алгоритмах и программировании. Ранее мы уже успели познакомиться с факториалами — сейчас на подходе большая статья про теорию вероятностей. В общем, оставайтесь на связи :)






